【2022版】基于矩阵分解的PCA 白化&ZCA白化
【2022版】基于矩阵分解的PCA 白化&ZCA白化
@author: Heisenberg
主成分分析(principal component analysis, PCA)是一种常用的数据降维算法。主要思想是将 n n n维的向量映射到 k k k维上,这 k k k维全新的正交特征也被成为主成分。通过计算数据矩阵 X X X的协方差矩阵 Σ \Sigma Σ,得到协方差矩阵的特征值特征向量,选择方差最大(也即特征值最大)的k个特征(坐标轴方向)组成的矩阵,以将原来的 X X X变换到新的空间上。
做whitening白化(亦作sphering,球化)的处理的条件:
- 使数据的不同维度去相关;
- 使数据每个维度的方差为1;
1、协方差矩阵及散度矩阵
在数据处理之前,先对数据矩阵 X X X做中心化,则样本方差为
S 2 = 1 n − 1 Σ i = 1 N ( x i − x ˉ ) 2 S^2=\frac{1}{n-1}\Sigma_{i=1}^{N}(x_i-\bar{x})^2 S2=n−11Σi=1N(xi−xˉ)2,用矩阵描述即 S 2 = 1 n − 1 X X T S^2=\frac{1}{n-1}\mathbf{X}\mathbf{X^T} S2=n−11XXT
而散度矩阵为
S 2 = Σ i = 1 n ( x i − x ˉ ) ( x i − x ˉ ) T S^2=\Sigma_{i=1}^{n}(\mathbf{x_i}-\mathbf{\bar{x}})(\mathbf{x_i}-\mathbf{\bar{x}})^{T} S2=Σi=1n(xi−xˉ)(xi−xˉ)T,即 S 2 = X X T S^2=\mathbf{X}\mathbf{X^T} S2=XXT
可以看到散度矩阵即协方差矩阵乘以(样本量-1)。二者的特征值和特征向量一样的。
基本思路即对 S 2 S^2 S2进行分解。
补充
如果是对列进行降维,则是对 S 2 = X T X S^2=\mathbf{X}^T\mathbf{X} S2=XTX进行矩阵分解。
2、特征值矩阵分解
2.1 特征值与特征向量
若一个向量 v v v是矩阵 A \mathbf{A} A的特征向量,则可以表示为 A v = λ v Av=\lambda v Av=λv,其中 λ \lambda λ称之为特征值, v v v是正交向量。
2.2 特征值分解矩阵
对于矩阵 A A A,有一组特征向量 v v v,将这组向量正交化单位化后,能得到一组正交单位向量。
A = Q Σ Q − 1 \mathbf{A}=Q\Sigma Q^{-1} A=QΣQ−1.
其中 Q Q Q是A的特征向量组成的矩阵, Σ \Sigma Σ是一个对角阵,对角线上的元素就是特征值。实对称矩阵都可以分解为实特征向量和实特征值。且只有方阵才可以进行特征值分解。
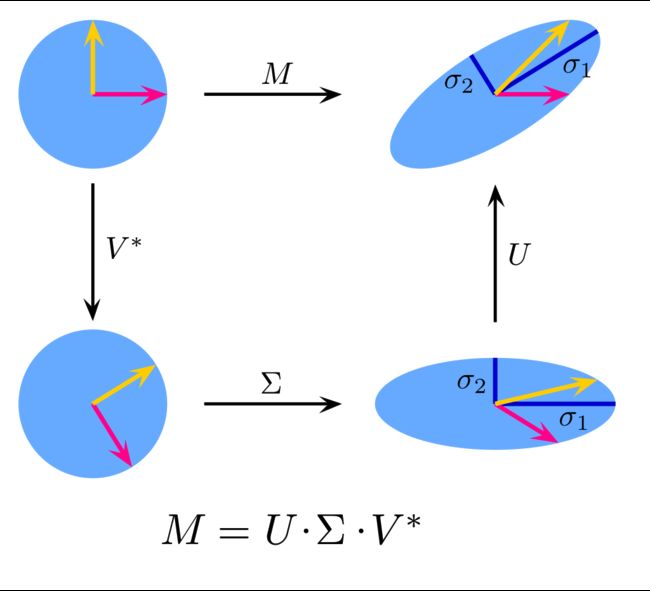
3、SVD矩阵分解
对于任意矩阵 A A A总是存在如下的奇异值分解:
A = U Σ V T A=U\Sigma V^T A=UΣVT
也即 A m × n = U m × m Σ m × n V n × n T A_{m\times n}=U_{m\times m}\Sigma_{m\times n}V^T_{n\times n} Am×n=Um×mΣm×nVn×nT, 展开形式如下所示:
( x 11 x 12 x 1 n ⋱ x m 1 x m n ) = ( u 11 u m 1 ⋱ u 1 m u m m ) ( σ 1 0 ⋱ σ r ⋱ 0 0 ) ( v 11 v 1 n ⋱ v n 1 v n n ) \left(\begin{array}{cccc} x_{11} & x_{12} & & x_{1 n} \\ & & \ddots & \\ x_{m 1} & & & x_{m n} \end{array}\right)=\left(\begin{array}{ccc} u_{11} & & u_{m 1} \\ & \ddots & \\ u_{1 m} & & u_{m m} \end{array}\right)\left(\begin{array}{cccc} \sigma_{1} & & & & 0 \\ & \ddots & & & \\ & & \sigma_{r} & \\ & & & \ddots & \\ 0 & & & & 0 \end{array}\right)\left(\begin{array}{ccc} v_{11} & & v_{1 n} \\ & \ddots & \\ v_{n 1} & & v_{n n} \end{array}\right) ⎝⎛x11xm1x12⋱x1nxmn⎠⎞=⎝⎛u11u1m⋱um1umm⎠⎞⎝⎜⎜⎜⎜⎛σ10⋱σr⋱00⎠⎟⎟⎟⎟⎞⎝⎛v11vn1⋱v1nvnn⎠⎞
其中,
U U U是左奇异向量,是 A A T AA^T AAT单位化后的特征向量构成的正交矩阵,有 U T U = I U^TU=I UTU=I, U T = U − 1 U^T=U^{-1} UT=U−1;
V V V是右奇异向量,是 A T A A^TA ATA单位化后的特征向量构成的正交矩阵,有 V T V = I V^TV=I VTV=I, V T = V − 1 V^T=V^{-1} VT=V−1,所以奇异值分解也可以写为 A V = U Σ AV=U\Sigma AV=UΣ;
Σ \Sigma Σ是 A T A A^TA ATA(或 A A T AA^T AAT)的特征值求平方根后的对角矩阵。
Remarks:
所以SVD分解能够同时按行按列进行降维:
X k × r ′ = U k × m T X m × n V n × r X^{\prime}_{k\times r}= U^T_{k\times m}X_{m\times n}V_{n\times r} Xk×r′=Uk×mTXm×nVn×r
图解:
图源自维基百科,可见左右奇异矩阵 U , V U,V U,V都是旋转坐标轴,对角矩阵 Σ \Sigma Σ是为了压缩数据矩阵。
4、基于特征值分解的PCA降维
4.1 基本步骤
对于数据矩阵 X = [ x 1 , x 2 , ⋯ , x n ] X=[x_1,x_2,\cdots,x_n] X=[x1,x2,⋯,xn]。其中 x i x_i xi都是列向量
- 去中心化。i.e. x i − x ˉ x_i-\bar{x} xi−xˉ
- 就算协方差矩阵 S 2 = 1 n X X T S^2=\frac{1}{n}\mathbf{X}\mathbf{X^T} S2=n1XXT(按行), S 2 = 1 n X T X S^2 = \frac{1}{n}\mathbf{X^T}\mathbf{X} S2=n1XTX(按列)
- 通过特征值分解法求 S 2 S^2 S2的特征值与特征向量。
- 对特征值按照从大到小的顺序,选取最大的 K K K个。
- 如果要按行降维,将对应的K个特征向量分别作为行向量组成特征向量矩阵 P P P.
- 如果要按列降维,将对应的K个特征向量分别作为列向量组成特征向量矩阵$P
- 将数据转换到K个特征向量构建的新空间中,i.e. Y k × n = P k × m X m × n Y_{k\times n}=P_{k\times m}X_{m \times n} Yk×n=Pk×mXm×n(按行)或 Y m × k = X m × n P n × k Y_{m\times k}=X_{m\times n}P_{n\times k} Ym×k=Xm×nPn×k
4.2 举例
举个栗子更形象些:
For 矩阵 X = ( − 1 − 1 0 2 0 − 2 0 0 1 1 ) X=\left(\begin{array}{ccccc}-1 & -1 & 0 & 2 & 0 \\ -2 & 0 & 0 & 1 & 1\end{array}\right) X=(−1−2−10002101)
-
对列做降维,类似于将特征整合。
-
求其协方差矩阵
S 2 = 1 5 ( − 1 − 2 − 1 0 0 0 2 1 0 1 ) ( − 1 − 1 0 2 0 − 2 0 0 1 1 ) = ( 1 − 1 5 0 − 4 5 − 2 5 − 1 5 1 5 0 2 5 0 0 0 0 0 0 − 4 5 2 5 0 1 1 5 − 2 5 0 0 1 5 1 5 ) S^2=\frac{1}{5}\left(\begin{array}{cc}-1 & -2 \\ -1 & 0 \\ 0 & 0 \\ 2 & 1 \\ 0 & 1\end{array}\right)\left(\begin{array}{ccccc}-1 & -1 & 0 & 2 & 0 \\ -2 & 0 & 0 & 1 & 1\end{array}\right)=\left(\begin{array}{ccccc}1 & -\frac{1}{5} & 0 & -\frac{4}{5}&-\frac{2}{5}\\ -\frac{1}{5} & \frac{1}{5} & 0 & \frac{2}{5}&0 \\ 0 & 0 & 0 & 0&0 \\ -\frac{4}{5} & \frac{2}{5} & 0 & 1&\frac{1}{5} \\ -\frac{2}{5} & 0 & 0 & \frac{1}{5}&\frac{1}{5}\end{array}\right) S2=51⎝⎜⎜⎜⎜⎛−1−1020−20011⎠⎟⎟⎟⎟⎞(−1−2−10002101)=⎝⎜⎜⎜⎜⎛1−510−54−52−5151052000000−54520151−52005151⎠⎟⎟⎟⎟⎞ -
求解得到特征值为 λ 1 = 2 , λ 2 = 2 5 \lambda_1=2,\lambda_2=\frac{2}{5} λ1=2,λ2=52, λ 3 = λ 4 = λ 5 = 0 \lambda_3=\lambda_4=\lambda_5=0 λ3=λ4=λ5=0,对应的标准化后的特征向量为
q 1 = ( − 3 20 1 20 0 3 20 1 20 ) , q 2 = ( − 1 2 − 1 2 0 − 1 2 1 2 ) , q 3 = q 4 = q 5 = 0 ∈ R 5 × 1 q_1=\left(\begin{array}{ccccc}-\frac{3}{\sqrt{20}}\\\frac{1}{\sqrt{20}}\\ 0 \\ \frac{3}{\sqrt{20}}\\\frac{1}{\sqrt{20}} \end{array}\right), q_2=\left(\begin{array}{ccccc}-\frac{1}{2}\\-\frac{1}{2}\\0\\-\frac{1}{2}\\\frac{1}{2} \end{array}\right), q_3=q_4=q_5=\mathbf{0}\in\mathbf{R}^{5\times1} q1=⎝⎜⎜⎜⎜⎜⎛−2032010203201⎠⎟⎟⎟⎟⎟⎞,q2=⎝⎜⎜⎜⎜⎛−21−210−2121⎠⎟⎟⎟⎟⎞,q3=q4=q5=0∈R5×1 -
选取K=2,则线性变换矩阵如下:
P = ( − 3 20 − 1 2 1 20 − 1 2 0 0 3 20 − 1 2 1 20 1 2 ) ∈ R 5 × 2 \mathbf{P}=\left(\begin{array}{ccccc}-\frac{3}{\sqrt{20}} & -\frac{1}{2}\\\frac{1}{\sqrt{20}}&-\frac{1}{2} \\ 0 & 0 \\ \frac{3}{\sqrt{20}} & -\frac{1}{2} \\ \frac{1}{\sqrt{20}} & \frac{1}{2} \end{array}\right)\in \mathbf{R}^{5\times2} P=⎝⎜⎜⎜⎜⎜⎛−2032010203201−21−210−2121⎠⎟⎟⎟⎟⎟⎞∈R5×2 -
则可得到 X PCA = X 2 × 5 P 5 × 2 = ( 5 − 1 5 1 ) X^{\text{PCA}}=X_{2\times5}P_{5\times 2}=\left(\begin{array}{cc}\sqrt{5} & -1 \\ \sqrt{5} & 1 \end{array}\right) XPCA=X2×5P5×2=(55−11)
-
-
对行做降维,类似于将样本分类、总结。
-
求其协方差矩阵
S 2 = 1 5 ( − 1 − 1 0 2 0 − 2 0 0 1 1 ) ( − 1 − 2 − 1 0 0 0 2 1 0 1 ) = ( 6 5 4 5 4 5 6 5 ) S^2=\frac{1}{5}\left(\begin{array}{ccccc}-1 & -1 & 0 & 2 & 0 \\ -2 & 0 & 0 & 1 & 1\end{array}\right)\left(\begin{array}{cc}-1 & -2 \\ -1 & 0 \\ 0 & 0 \\ 2 & 1 \\ 0 & 1\end{array}\right)=\left(\begin{array}{cc}\frac{6}{5} & \frac{4}{5} \\ \frac{4}{5} & \frac{6}{5}\end{array}\right) S2=51(−1−2−10002101)⎝⎜⎜⎜⎜⎛−1−1020−20011⎠⎟⎟⎟⎟⎞=(56545456) -
求解得到特征值为 λ 1 = 2 , λ 2 = 2 5 \lambda_1=2,\lambda_2=\frac{2}{5} λ1=2,λ2=52,对应的特征向量为 q 1 = [ 1 , 1 ] T , q 2 = [ − 1 , 1 ] T q_1=[1,1]^T, q_2=[-1,1]^T q1=[1,1]T,q2=[−1,1]T
-
将特征向量标准化得到 q 1 = [ 1 2 , 1 2 ] T , q 2 = [ − 1 2 , 1 2 ] T q_1=[\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}]^T, q_2=[-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}]^T q1=[21,21]T,q2=[−21,21]T
-
则线性变换矩阵 P = ( 1 2 1 2 − 1 2 1 2 ) P=\left(\begin{array}{cc}\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}\end{array}\right) P=(21−212121)
-
选取K=1,则可得到
-
Y 1 × 5 = P 1 × 2 X 2 × 5 = ( 1 2 1 2 ) ( − 1 − 1 0 2 0 − 2 0 0 1 1 ) = ( − 3 2 − 1 2 0 3 2 − 1 2 ) Y_{1\times 5}=P_{1\times 2}X_{2\times 5}\\=\left(\begin{array}{ll} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{array}\right)\left(\begin{array}{ccccc} -1 & -1 & 0 & 2 & 0 \\ -2 & 0 & 0 & 1 & 1 \end{array}\right)\\=\left(\begin{array}{lllll} -\frac{3}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 0 & \frac{3}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{array}\right) Y1×5=P1×2X2×5=(2121)(−1−2−10002101)=(−23−21023−21)
5、基于SVD分解的PCA降维
5.1 基本步骤
对于数据矩阵 X = [ x 1 , x 2 , ⋯ , x n ] X=[x_1,x_2,\cdots,x_n] X=[x1,x2,⋯,xn]。其中 x i x_i xi都是列向量
-
去中心化。i.e. x i − x ˉ x_i-\bar{x} xi−xˉ
-
就算协方差矩阵 S row 2 = 1 n − 1 X X T S^2_{\text{row}}=\frac{1}{n-1}\mathbf{X}\mathbf{X^T} Srow2=n−11XXT和 S col 2 = 1 n − 1 X T X S^2_{\text{col}}=\frac{1}{n-1}\mathbf{X^T}\mathbf{X} Scol2=n−11XTX(SVD分解能同时按行、按列降维。)
-
通过SVD分解法求两个 S 2 S^2 S2的特征值与特征向量。
-
对特征值按照从大到小的顺序,选取最大的 K K K个。
将对应的K个特征向量中,U分别作为行向量,V分别作为列向量组成特征向量矩阵 P P P
-
将数据转换到K个特征向量构建的新空间中。
5.2 优点
- 某些SVD算法不用先求 X X T XX^T XXT就求出右奇异矩阵,降低运算开销。
- 左右两个奇异矩阵可以在行和列两个方向对数据进行压缩。i.e. Y m × k = X m × n V n ∗ k T Y_{m\times k}=X_{m\times n}V^T_{n*k} Ym×k=Xm×nVn∗kT ,右奇异矩阵对列进行压缩; Y k × n = U k × m T X m × n Y_{k\times n}=U^T_{k\times m}X_{m \times n} Yk×n=Uk×mTXm×n,左奇异矩阵对行数进行特征压缩。(在此说的维度转置与否都是要与原矩阵对应的)
5.3 举例
举个栗子:
对于矩阵 A = ( 3 2 2 2 3 − 2 ) A=\left(\begin{array}{ccc}3 & 2 & 2 \\ 2 & 3 & -2\end{array}\right) A=(32232−2),可得到:
A A T = ( 17 8 8 17 ) , A T A = ( 13 12 2 12 13 − 2 2 − 2 8 ) A A^{T}=\left(\begin{array}{cc}17 & 8 \\ 8 & 17\end{array}\right), \quad A^{T} A=\left(\begin{array}{ccc}13 & 12 & 2 \\ 12 & 13 & -2 \\ 2 & -2 & 8\end{array}\right) AAT=(178817),ATA=⎝⎛131221213−22−28⎠⎞
- 对 A A T AA^T AAT求特征值为 λ 1 = 25 , λ 2 = 9 \lambda_1=25,\lambda_2=9 λ1=25,λ2=9; 特征向量为 u 1 = ( 1 2 , 1 2 ) u 2 = ( 1 2 , − 1 2 ) u_{1}=\left(\begin{array}{c}\frac{1}{\sqrt{2}} , \frac{1}{\sqrt{2}}\end{array}\right) \quad u_{2}=\left(\begin{array}{c}\frac{1}{\sqrt{2}}, -\frac{1} {\sqrt{2}}\end{array}\right) u1=(21,21)u2=(21,−21)
- 对 A T A A^TA ATA求特征值为 λ 1 = 25 , λ 2 = 9 , λ 3 = 0 \lambda_1=25,\lambda_2=9,\lambda_3=0 λ1=25,λ2=9,λ3=0; 特征向量为 v 1 = ( 1 / 2 1 / 2 0 ) v 2 = ( 1 / 18 − 1 / 18 4 / 18 ) v 3 = ( 2 / 3 − 2 / 3 − 1 / 3 ) v_{1}=\left(\begin{array}{c}1 / \sqrt{2} \\ 1 / \sqrt{2} \\ 0\end{array}\right) \quad v_{2}=\left(\begin{array}{c}1 / \sqrt{18} \\ -1 / \sqrt{18} \\ 4 / \sqrt{18}\end{array}\right) \quad v_{3}=\left(\begin{array}{c}2 / 3 \\ -2 / 3 \\ -1 / 3\end{array}\right) v1=⎝⎛1/21/20⎠⎞v2=⎝⎛1/18−1/184/18⎠⎞v3=⎝⎛2/3−2/3−1/3⎠⎞
- 则A的SVD分解可以写作如下:
A = U S V T = ( 1 / 2 1 / 2 1 / 2 − 1 / 2 ) ( 5 0 0 0 3 0 ) ( 1 / 2 1 / 2 0 1 / 18 − 1 / 18 4 / 18 2 / 3 − 2 / 3 − 1 / 3 ) A=U S V^{T}=\left(\begin{array}{cc} 1 / \sqrt{2} & 1 / \sqrt{2} \\ 1 / \sqrt{2} & -1 / \sqrt{2} \end{array}\right)\left(\begin{array}{ccc} 5 & 0 & 0 \\ 0 & 3 & 0 \end{array}\right)\left(\begin{array}{rrr} 1 / \sqrt{2} & 1 / \sqrt{2} & 0 \\ 1 / \sqrt{18} & -1 / \sqrt{18} & 4 / \sqrt{18} \\ 2 / 3 & -2 / 3 & -1 / 3 \end{array}\right) A=USVT=(1/21/21/2−1/2)(500300)⎝⎛1/21/182/31/2−1/18−2/304/18−1/3⎠⎞
- 选取K=2,则对A进行列的压缩可以得到:
Y ( 2 × 2 ) = A ( 2 × 3 ) V ( 3 ∗ 2 ) Y_{(2\times 2)}=A_{(2\times 3)}V_{(3*2)} Y(2×2)=A(2×3)V(3∗2)
也即
Y = ( 3 2 2 2 3 − 2 ) ( 1 / 2 1 / 18 1 / 2 − 1 / 18 0 4 / 18 ) = ( 5 / 2 3 / 2 5 / 2 − 3 / 2 ) Y=\left(\begin{array}{ccc}3 & 2 & 2 \\ 2 & 3 & -2\end{array}\right)\left(\begin{array}{ccc}1 / \sqrt{2} & 1 / \sqrt{18} \\ 1 / \sqrt{2} & -1 / \sqrt{18} \\0 & 4 / \sqrt{18} \end{array}\right) =\left(\begin{array}{cc}5/\sqrt{2} & 3 / \sqrt{2} \\ 5/\sqrt{2} & -3 / \sqrt{2}\end{array}\right) Y=(32232−2)⎝⎛1/21/201/18−1/184/18⎠⎞=(5/25/23/2−3/2)
- 选取K=1,对A进行行的压缩可以得到:
Y ( 1 × 3 ) = U ( 1 × 2 ) T A ( 2 × 3 ) Y_{(1\times 3)}=U^T_{(1\times 2)}A_{(2\times 3)} Y(1×3)=U(1×2)TA(2×3)
Y = ( 1 / 2 1 / 2 ) ( 3 2 2 2 3 − 2 ) = ( 5 / 2 5 / 2 0 ) Y=\left(\begin{array}{cc}1 / \sqrt{2} & 1 / \sqrt{2}\end{array}\right)\left(\begin{array}{ccc}3 & 2 & 2 \\ 2 & 3 & -2\end{array}\right)=\left(\begin{array}{ccc}5 / \sqrt{2} & 5 / \sqrt{2}& 0\end{array}\right) Y=(1/21/2)(32232−2)=(5/25/20)
其中 u 1 = ( 1 / 2 1 / 2 ) u_{1}=\left(\begin{array}{c}1 / \sqrt{2} \\ 1 / \sqrt{2}\end{array}\right) u1=(1/21/2)称之为第一主成分,以此类推。
5.4 方差贡献率
对于特征值对角矩阵 Σ = ( σ 1 ⋱ σ r ) ( r × r ) \Sigma=\left(\begin{array}{ccc} \sigma_{1} & & \\ & \ddots & \\ & & \sigma_{r} \end{array}\right)_{(r\times r)} Σ=⎝⎛σ1⋱σr⎠⎞(r×r)
如果我们想保留99%的方差贡献率则使得 α i = Σ i = 1 k σ i Σ j = 1 r σ j ≥ 0.99 \alpha_i = \frac{\Sigma_{i=1}^k\sigma_i}{\Sigma_{j=1}^r\sigma_j}\geq0.99 αi=Σj=1rσjΣi=1kσi≥0.99即可.
Generally,75%以上就合格。
Remarks
原则上来说 A A A矩阵的特征值分解的 Q Q Q矩阵和A矩阵的 V T V^T VT矩阵是相等的。但是由于某些包算法上的区别使得列的排列顺序、正负号、数值大小有细微的区别,但仍是相等的。(排列顺序、正负号不改变矩阵相等是因为Q,V都是orthography matrix,正交矩阵保证该性质。数值差异大概率是因为下面PArt6中正则化导致的。)
如该例中
In [2]: a = np.array([[3,2,2],[2,3,-2]])
In [3]: a
Out[3]:
array([[ 3, 2, 2],
[ 2, 3, -2]])
In [5]: eig_vals,eig_vecs=np.linalg.eig(a.T@a)
In [6]: eig_vals
Out[6]: array([2.50000000e+01, 3.44694725e-15, 9.00000000e+00])
In [11]: eig_vecs
Out[11]:
array([[-7.07106781e-01, -6.66666667e-01, 2.35702260e-01],
[-7.07106781e-01, 6.66666667e-01, -2.35702260e-01],
[-1.16847159e-17, 3.33333333e-01, 9.42809042e-01]])
In [12]: u,s,vh = np.linalg.svd(a)
In [23]: vh.T
Out[23]:
array([[-7.07106781e-01, -2.35702260e-01, -6.66666667e-01],
[-7.07106781e-01, 2.35702260e-01, 6.66666667e-01],
[-6.47932334e-17, -9.42809042e-01, 3.33333333e-01]])
引自PCA SVD原理详解及应用
最后说一下两者的联系,其实svd可以用来做pca的,因为在pca阶段我们主要求得是 X X T XX^T XXT特征值和特征向量,对吧(暂不考虑减去均值),而在求svd的左奇异矩阵(U)过程中,也是求得是 X X T XX^T XXT特征值和特征向量对吧,也就是说这里的SVD奇异值的平方就是pca中的特征值对吧,其实在SVD的分解过程中,不用像我们上面讨论的那样先求 , 特征值和特征向量方法进行分解,而是有很多快速算法,但我们可以根据SVD的结果进行PCA对吧,其实scikit-learn内部的PCA也是用SVD做的
6、正则化
若在举例5.3的步骤2中不对特征向量做标准化
即 X P C A − W h i t e = Σ − 1 2 U T X = [ 1 λ 1 0 0 0 ⋱ 0 0 0 1 λ n ] X r o t a t e X_{PCA-White}=\Sigma^{-\frac{1}{2}}U^TX=\left[\begin{array}{ccc} \frac{1}{\sqrt{\lambda_{1}}} & 0 & 0 \\ 0 & \ddots & 0 \\ 0 & 0 & \frac{1}{\sqrt{\lambda_{n}}} \end{array}\right]X_{rotate} XPCA−White=Σ−21UTX=⎣⎡λ11000⋱000λn1⎦⎤Xrotate
Proof:
S P C A hite 2 = 1 m X PCAwhite X PCAwhite T = Σ − 1 2 U T ( 1 m X X T ) U ( Σ − 1 2 ) T = Σ − 1 2 U T S 2 U Σ − 1 2 ∵ 对角阵 = Σ − 1 2 ( U T U ) Σ ( U T U ) Σ − 1 2 ∵ SVD分解 = Σ − 1 2 I Σ I Σ − 1 2 ∵ 酉矩阵 U U T = U T U = I = I \begin{aligned} S^2_{P C A \text { hite }} &=\frac{1}{m} X_{\text {PCAwhite }} X_{\text {PCAwhite }}^{T} \\ &=\Sigma^{-\frac{1}{2}} U^{T}\left(\frac{1}{m} X X^{T}\right) U\left(\Sigma^{-\frac{1}{2}}\right)^{T} \\ &=\Sigma^{-\frac{1}{2}} U^{T} S^2 U \Sigma^{-\frac{1}{2}}\quad \because \text{对角阵}\\ &=\Sigma^{-\frac{1}{2}}\left(U^{T} U\right) \Sigma\left(U^{T} U\right) \Sigma^{-\frac{1}{2}}\because \text{SVD分解} \\ &=\Sigma^{-\frac{1}{2}} I \Sigma I \Sigma^{-\frac{1}{2}}\because \text{酉矩阵}UU^T=U^TU=I \\ &=I \end{aligned} SPCA hite 2=m1XPCAwhite XPCAwhite T=Σ−21UT(m1XXT)U(Σ−21)T=Σ−21UTS2UΣ−21∵对角阵=Σ−21(UTU)Σ(UTU)Σ−21∵SVD分解=Σ−21IΣIΣ−21∵酉矩阵UUT=UTU=I=I
通常在实践中,一般选 X P C A − W h i t e , i = X r o t , i λ i + ϵ X_{PCA-White,i}=\frac{X_{rot,i}}{\sqrt{\lambda_i+\epsilon}} XPCA−White,i=λi+ϵXrot,i, ϵ = 1 0 − 5 \epsilon=10^{-5} ϵ=10−5.
原因:
- 有时一些特征值在数值上接近0,在缩放步骤时将导致除以一个接近0的值;这可能使数据上溢或造成数值不稳定;
- 对图像来说,正则化项对输入图像也有一些平滑去噪(或低通滤波)的作用,可改善学习到的特征。
7、ZAC白化
Zero-phase Component Analysis Whitening 零相位成分分析白化
PCA and ZCA whitening differ only by a rotation.
——《Neural Networks: Tricks of the Trade》
ZCA白化只是在PCA白化的基础上做了一个旋转操作,使得白化之后的数据映射回源空间更加的接近原始数据。
Y Z A C , ( m × n ) = U ( m × k ) Y P C A , ( k × n ) = U ( m × k ) U ( k × m ) T X m × n Y_{ZAC,(m\times n)=U_{(m\times k)}Y_{PCA,(k\times n)}}=U_{(m\times k)}U^T_{(k\times m)}X_{m \times n} YZAC,(m×n)=U(m×k)YPCA,(k×n)=U(m×k)U(k×m)TXm×n
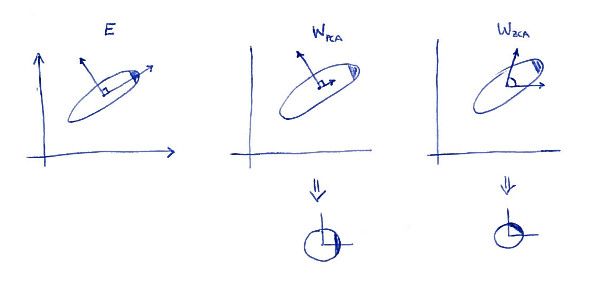
下图可以更有助加深理解。
图片源自StackChange.
图1为原始数据,图2为PCA选取的最大方差方向的新坐标轴,下方对应的为映射到新坐标轴后,原始阴影部分数据在新坐标空间的最东边,而图3进行ZAC坐标旋转之后,将阴影部分数据转到了新坐标空间的东北部分。
Proof:
∑ ZCAwhite = 1 m X ZCAwhite X ZCAwhite T = U 1 m X PCAwhile X PCAwhite U T = U I U T = I \begin{aligned} \sum_{\text {ZCAwhite }} &=\frac{1}{m} X_{\text {ZCAwhite }} X_{\text {ZCAwhite }}^{T} \\ &=U \frac{1}{m} X_{\text {PCAwhile }} X_{\text {PCAwhite }} U^{T} \\ &=U I U^{T} \\ &=I \end{aligned} ZCAwhite ∑=m1XZCAwhite XZCAwhite T=Um1XPCAwhile XPCAwhite UT=UIUT=I
可见其仍能保证白化的合法化,协方差矩阵是对角阵的单位矩阵。
举例1(特征值分解):
Y Z C A , ( 2 × 5 ) = U ( 2 × 1 ) Y P C A , ( 1 × 5 ) Y_{ZCA,(2\times5)}=U_{(2\times1)}Y_{PCA,(1\times5)} YZCA,(2×5)=U(2×1)YPCA,(1×5)
Y Z A C = ( 1 2 1 2 ) ( − 3 2 − 1 2 0 3 2 − 1 2 ) = ( − 3 / 2 − 1 / 2 0 3 / 2 − 1 / 2 − 3 / 2 − 1 / 2 0 3 / 2 − 1 / 2 ) Y_{ZAC}=\left(\begin{array}{ll} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{array}\right)\left(\begin{array}{lllll} -\frac{3}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 0 & \frac{3}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{array}\right)=\left(\begin{array}{ccccc}-3/2 & -1/2 & 0 & 3/2 & -1/2 \\ -3/2 & -1/2 & 0 & 3/2 & -1/2\end{array}\right) YZAC=(2121)(−23−21023−21)=(−3/2−3/2−1/2−1/2003/23/2−1/2−1/2)
举例2(SVD分解):
Y Z C A , ( 2 × 3 ) = U ( 2 × 1 ) Y P C A , ( 1 × 3 ) Y_{ZCA,(2\times 3)}=U_{(2\times1)}Y_{PCA,(1\times 3)} YZCA,(2×3)=U(2×1)YPCA,(1×3)
Y Z C A = ( 1 / 2 1 / 2 ) ( 5 / 2 5 / 2 0 ) = ( 5 / 2 5 / 2 0 5 / 2 5 / 2 0 ) Y_{ZCA}=\left(\begin{array}{c}1 / \sqrt{2} \\ 1 / \sqrt{2}\end{array}\right)\left(\begin{array}{ccc}5 / \sqrt{2} & 5 / \sqrt{2}& 0\end{array}\right)=\left(\begin{array}{ccc}5/2 & 5/2 & 0 \\ 5/2 & 5/2 & 0\end{array}\right) YZCA=(1/21/2)(5/25/20)=(5/25/25/25/200)
8、应用
LSI应用
在机器学习中的数学(5)-强大的矩阵奇异值分解(SVD)及其应用中引用《数学之美》中吴军老师的话:
“三个矩阵有非常清楚的物理含义。第一个矩阵X中的每一行表示意思相关的一类词,其中的每个非零元素表示这类词中每个词的重要性(或者说相关性),数值越大越相关。最后一个矩阵Y中的每一列表示同一主题一类文章,其中每个元素表示这类文章中每篇文章的相关性。中间的矩阵则表示类词和文章雷之间的相关性。因此,我们只要对关联矩阵A进行一次奇异值分解,w 我们就可以同时完成了近义词分类和文章的分类。(同时得到每类文章和每类词的相关性)。”
参考资料
Machine Learning — Singular Value Decomposition (SVD) & Principal Component Analysis (PCA)
主成分分析(PCA)原理详解
斯坦佛UFLDL PCA Whitening
What is the difference between ZCA whitening and PCA whitening?
LDA、PCA、ZCA、ICA回顾
PCA SVD原理详解及应用
机器学习中的数学(5)-强大的矩阵奇异值分解(SVD)及其应用