机器学习笔记之条件随机场(四)建模对象描述(参数表示vs向量表示)

引言

上一节介绍了最大熵马尔可夫模型(Maximum Entropy Markov Model,MEMM)中的标注偏置问题，本节将介绍条件随机场(Condition Random Field,CRF)，并介绍它的建模思想以及概率密度函数$\mathcal{P}(\mathcal{I}\mid \mathcal{O})$。

回顾：

最大团与势函数

在马尔可夫随机场的结构表示中介绍过极大团(Maximum Clique)。极大团表示马尔可夫随机场中结点的子集，该子集需要满足的条件是：子集内部任意两结点之间都有边连接，并且在该子集中加入任意一个结点后都不再形成团。
已知马尔可夫随机场示例如下：

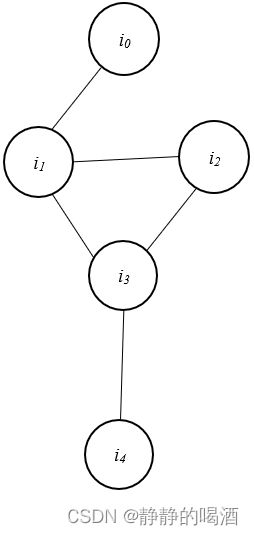
上图中一共包含$3$个极大团，分别是：
例如极大团$\{i_1,i_2,i_3\}$,首先，该三个结点之间两两存在边相连，如果再加入一个结点$i_0$,由于$(i_0,i_2),(i_0,i_3)$之间不存在边相连，因此无法构成极大团。
$$x_{{\mathcal{C}}_1}=\{i_0,i_1\},x_{{\mathcal{C}}_2}=\{i_1,i_2,i_3\},x_{{\mathcal{C}}_3}=\{i_3,i_4\}$$
而势函数(Potential Function)表示最大团内部结点之间的一种关系，通过这种关系描述马尔可夫随机场中结点的联合概率分布：

• 假设数据集合$\mathcal{X}$中的$p$个维度/特征划分为$\mathcal{K}$个极大团：
  注意，这里并没有说$p$个特征一定会出现$p$个结点，按照概率图中结点的定义，每个结点包含1个/多个特征。但这里，结点数量显然不是重点。
  $$\{x_{{\mathcal{C}}_1},x_{{\mathcal{C}}_2},\cdots ,x_{{\mathcal{C}}_{\mathcal{K}}}\}$$
• 联合概率分布$\mathcal{P}(\mathcal{X})$表示为：
  $$\mathcal{P}(\mathcal{X})=\frac{1}{\mathcal{Z}}\prod _{i=1}^{\mathcal{K}}{\psi }_i(x_{{\mathcal{C}}_i})$$
  其中，${\psi }_i(x_{{\mathcal{C}}_i})$表示极大团$x_{{\mathcal{C}}_i}$的势函数，是一个 非负实函数；而$\mathcal{Z}$表示规范化因子，具体表示如下：
  $$\mathcal{Z}=\sum _{x_1,\cdots ,x_p}\prod _{i=1}^{\mathcal{K}}{\psi }_i(x_{{\mathcal{C}}_i})$$

最大熵模型

最大熵模型的原理是：满足给定约束条件的模型集合中选取熵最大的模型。并且在最大熵原理与指数族分布的关系中通过推导确定了满足给定约束条件情况下，满足约束条件下熵最大的分布是指数族分布(Exponential Family of Distributions)。
最大熵模型本质上就是求解‘条件概率分布’的一种方式。

最大熵模型公式表示如下：
最大熵模型公式推导给大家推荐一篇~传送门
$$\mathcal{P}(\mathcal{Y}\mid \mathcal{X})=\frac{1}{\mathcal{Z}}\exp \left[\sum _{i=1}^N{\lambda }_i{f}_i(\mathcal{X},\mathcal{Y})\right]$$
其中$f_i(\mathcal{X},\mathcal{Y})$表示 特征函数(Feature Funtion),${\lambda }_i$表示需要学习的特征权值：
$$f_i(\mathcal{X},\mathcal{Y})=\{\begin{array}{l}1\mathcal{X},\mathcal{Y}\to \text{ Satisfy facts}\\ 0otherwise\end{array}$$
$\mathcal{Z}$表示归一化因子；
$$\mathcal{Z}=\sum _{\mathcal{Y}}\exp \left[\sum _{i=1}^N{\lambda }_i{f}_i(\mathcal{X},\mathcal{Y})\right]$$

条件随机场

在MEMM介绍过程中，提到了标注偏置问题(Label bias Problem)。其核心思想是：MEMM虽然引入了观测变量${\mathcal{O}}_{1:T}$的全局影响，但是当训练数据分布不均衡时，会导致内部概率分布相差很大，从而导致概率分布差异性对条件概率结果影响小，最终使状态转移结果与给定观测结果不匹配。

条件随机场的核心时将 最大熵马尔可夫模型中隐变量之间有向边的方向性抹除。从而有如下形式：
这是视频中的描述格式，但西瓜书中的描述格式，将观测变量到隐变量有向边的方向性也去掉了。见第二张图。


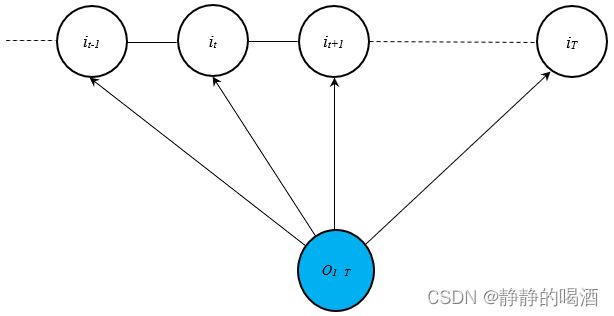
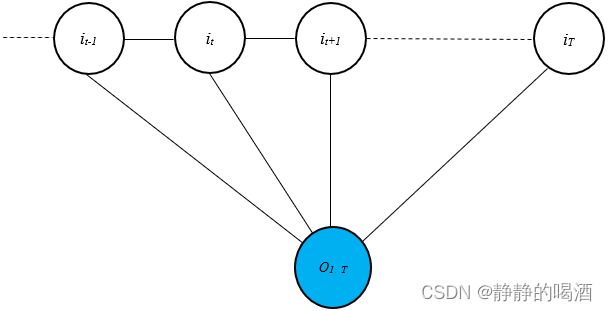
上述图表示的是最常用的链式条件随机场(Chain-Structured CRF)，条件随机场中随机场的部分只是隐变量的部分，而观测变量部分${\mathcal{O}}_{1:T}$在概率图中仅表示条件的概念。

条件随机场的合理性

条件随机场的合理性体现在两方面：

• 条件随机场是 概率判别模型，它针对$\mathcal{P}(\mathcal{I}\mid \mathcal{O})$进行建模。
• 条件随机场是一个无向图/马尔可夫随机场。

由于是无向图，因此 无法直接使用因子分解直接写出$\mathcal{P}(\mathcal{I}\mid \mathcal{O})$。这里使用势函数和图结构中的团来定义 条件概率/概率密度函数$\mathcal{P}(\mathcal{I}\mid \mathcal{O})$：
这里针对‘链式条件随机场’进行推导。

• 假设整个概率图模型中一共包含$\mathcal{K}$个极大团：
  从马尔可夫随机场的角度理解，它求解的并不是条件概率分布$\mathcal{P}(\mathcal{I}\mid \mathcal{O})$,而是基于‘马尔可夫随机场’中隐变量$\mathcal{I}$的联合概率分布。
  $$\mathcal{P}(\mathcal{I}\mid \mathcal{O})=\frac{1}{\mathcal{Z}}\prod _{k=1}^{\mathcal{K}}{\psi }_k(i_{{\mathcal{C}}_k})$$

• 其中$i_{{\mathcal{C}}_k}$表示编号为$k$的极大团。由于${\psi }_k(i_{{\mathcal{C}}_k})$是非负实函数，因此将上式修改为：
  $$\mathcal{P}(\mathcal{I}\mid \mathcal{O})=\frac{1}{\mathcal{Z}}\prod _{k=1}^{\mathcal{K}}\exp [-{\mathbb{E}}_k(i_{{\mathcal{C}}_k})]$$
  其中$-{\mathbb{E}}_k(i_{{\mathcal{C}}_k})$称为能量函数，继续展开，将$\exp$和$\prod$调换位置，有：
  能量函数在‘马尔可夫随机场’中并没有扩展介绍。依然是在介绍玻尔兹曼机时再去介绍能量函数。这里仅将其视作一个函数即可。这里将$-{\mathbb{E}}_k(i_{{\mathcal{C}}_k})$替换为$f_k(i_{{\mathcal{C}}_k})$,只是换了一个函数表示。
  $$\mathcal{P}(\mathcal{I}\mid \mathcal{O})=\frac{1}{\mathcal{Z}}\exp \sum _{k=1}^{\mathcal{K}}{f}_k(i_{{\mathcal{C}}_k})$$
  观察这个链式的马尔可夫随机场，由于链式结构，其最大团只能是两个隐变量结点组成的团结构，因此将最大团数量$\mathcal{K}$使用时刻$T$进行表示($\mathcal{O}$表示观测变量输入)：
  个人认为有争议的点：

  • 如果将$\mathcal{O}$也算作马尔可夫随机场的结点，也就是‘西瓜书’中描述的马尔可夫随机场，那么最开始的‘极大团’中必然含$\mathcal{O}$，那求解的就不是$\mathcal{P}(\mathcal{I}\mid \mathcal{O})$,而是$\mathcal{P}(\mathcal{I},\mathcal{O})$。
  • 如果$\mathcal{O}$不算作马尔可夫随机场的结点，也就是‘视频’中描述的马尔可夫随机场，那么$f_k(i_{{\mathcal{C}}_k})\to f_t(i_t,i_{t+1},\mathcal{O})$这种写法是将$\mathcal{O}$直接强行加入。因为$\mathcal{O}$确实不是‘极大团’$i_{{\mathcal{C}}_k}$中的元素。

  个人比较倾向于第二种解释，因为$f_t(i_t,i_{t+1},\mathcal{O})$可能已经描述的不是概率分布，而是一种关联关系。这里将$\mathcal{O}$视作‘观测变量输入’即可。
为了方便下面公式的表达，这里假设存在一个$i_{T+1}$结点满足下面公式,并将其消去。
  $$\begin{array}{rl}\mathcal{P}(\mathcal{I}\mid \mathcal{O})& =\frac{1}{\mathcal{Z}}\exp \sum _{t=1}^T{f}_t(i_t,i_{t+1},\mathcal{O})\\ & =\frac{1}{\mathcal{Z}}\exp \left[\sum _{t=1}^{T-1}{f}_t(i_t,i_{t+1},\mathcal{O})+f_T(i_T,\mathcal{O})\right]\end{array}$$
  上述公式中$t$既表示特征函数的下标，也表示隐变量的下标。由于链式结构，所有的特征函数针对的极大团格式均相同(见红色椭圆部分)：
  
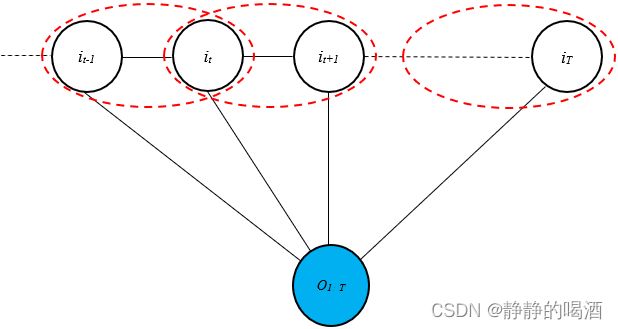
  因此，将特征函数的下标$t$消除：
  即所有极大团均使用‘同一款特征函数’表示极大团结构。
  $$\mathcal{P}(\mathcal{I}\mid \mathcal{O})=\frac{1}{\mathcal{Z}}\exp \left[\sum _{t=1}^{T-1}f(i_t,i_{t+1},\mathcal{O})+f(i_T,\mathcal{O})\right]$$
  观察连加号中的项：$f(i_t,i_{t+1},\mathcal{O})$，将其划分成两个部分：

  • 关于单个结点与观测变量的函数：假设存在$\mathcal{L}$个项，定义其函数为$g_l(l=1,2,\cdots ,\mathcal{L})$，并给对应函数分配学习函数${\eta }_l(l=1,2,\cdots ,\mathcal{L})$，其结果表示如下：
    $$\sum _{l=1}^{\mathcal{L}}{\eta }_l\cdot g_l(i_t,\mathcal{O})$$
  • 关于相邻结点与观测变量的函数：假设存在$\mathcal{M}$个项，定义其函数为$s_m(m=1,2,\cdots ,\mathcal{M})$，并给对应函数分配学习函数${\lambda }_m(m=1,2,\cdots ,\mathcal{M})$，其结果表示如下：
    $$\sum _{m=1}^{\mathcal{M}}{\lambda }_m\cdot s_m(i_{t+1},i_t,\mathcal{O})$$

  至此，$\mathcal{P}(\mathcal{I}\mid \mathcal{O})$表示如下：
  最后一项$f(i_T,\mathcal{O})$同样是‘关于单个结点与观测变量的函数’，因此也将其展开。
  $$\begin{array}{rl}\mathcal{P}(\mathcal{I}\mid \mathcal{O})& =\frac{1}{\mathcal{Z}}\exp \left[\sum _{t=1}^{T-1}f(i_t,i_{t+1},\mathcal{O})+f(i_T,\mathcal{O})\right]\\ & =\frac{1}{\mathcal{Z}}\exp \left\{\sum _{t=1}^{T-1}\left[\sum _{l=1}^{\mathcal{L}}{\eta }_l\cdot g_l(i_t,\mathcal{O})+\sum _{m=1}^{\mathcal{M}}{\lambda }_m\cdot s_m(i_{t+1},i_t,\mathcal{O})\right]+\sum _{l=1}^{\mathcal{L}}{\eta }_l\cdot g_l(i_T,\mathcal{O})\right\}\end{array}$$
  继续展开，并将$f(i_T,\mathcal{O})$项合并，最终得到结果如下：
  $$\mathcal{P}(\mathcal{I}\mid \mathcal{O})=\frac{1}{\mathcal{Z}}\exp \left[\sum _{t=1}^{T-1}\sum _{m=1}^{\mathcal{M}}{\lambda }_m\cdot s_m(i_{t+1},i_t,\mathcal{O})+\sum _{t=1}^T\sum _{l=1}^{\mathcal{L}}{\eta }_l\cdot g_l(i_t,\mathcal{O})\right]$$
  称$s_m$为转移特征函数(Transition Feature Function)，称$g_l$为状态特征函数(State Feature Function)，其中${\lambda }_m,{\eta }_l$是对应需要学习的模型参数。

个人理解：条件随机场PDF的表示形式

关于上述公式的替换过程，其替换结果已经非常接近最大熵模型对于$\mathcal{P}(\mathcal{I}\mid \mathcal{O})$的表达形式。从本质上观察，其就是使用最大熵模型对极大团的势函数进行描述。针对链式条件随机场，任意一个时刻$t$的极大团表示如下：

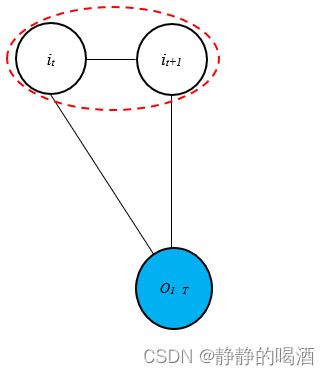
该极大团的势函数大致表示如下：
$$\begin{array}{rl}\frac{1}{\mathcal{Z}}{\psi }_t(i_{{\mathcal{C}}_t})& =\frac{1}{\mathcal{Z}}\exp f_t(i_t,i_{t+1},\mathcal{O})\\ & =\frac{1}{\mathcal{Z}}\exp \left[\sum _{l=1}^{\mathcal{L}}{\eta }_l\cdot g_l(i_t,\mathcal{O})+\sum _{m=1}^{\mathcal{M}}{\lambda }_m\cdot s_m(i_{t+1},i_t,\mathcal{O})\right]\\ & =\frac{1}{\mathcal{Z}}\exp \left[\sum _{l=1}^{\mathcal{L}}{\eta }_l\cdot g_l(i_t,\mathcal{O})\right]\cdot \exp \left[\sum _{m=1}^{\mathcal{M}}{\lambda }_m\cdot s_m(i_{t+1},i_t,\mathcal{O})\right]\end{array}$$
对比最大熵马尔可夫模型使用最大熵模型求解$\mathcal{P}(i_t\mid i_{t-1},\mathcal{O})$基本相同：
$$\mathcal{P}(i_t\mid i_{t-1},\mathcal{O})=\frac{1}{\mathcal{Z}}\exp \left[\sum _a{\lambda }_a{f}_a(i_t,i_{t-1},\mathcal{O})\right]$$
基于上述描述，由于链式条件随机场极大团形状的特殊性，我们可以将${\psi }_t(i_{{\mathcal{C}}_t})$看成两步操作：

• 通过状态特征函数，可以近似求解给定观测变量$\mathcal{O}$的条件下，$i_t$的条件概率$\mathcal{G}(i_t\mid \mathcal{O})$：
  $$\mathcal{G}(i_t\mid \mathcal{O})\to \exp \left[\sum _{l=1}^{\mathcal{L}}{\eta }_l\cdot g_l(i_t,\mathcal{O})\right]$$
• 通过转移特征函数，可以近似求解给定观测变量$\mathcal{O}$和隐变量$i_t$的条件下，$i_{t+1}$的条件概率$\mathcal{Q}(i_{t+1}\mid i_t,\mathcal{O})$：
  $$\mathcal{Q}(i_{t+1}\mid i_t,\mathcal{O})\to \exp \left[\sum _{m=1}^{\mathcal{M}}{\lambda }_m\cdot s_m(i_{t+1},i_t,\mathcal{O})\right]$$
• 最终通过 条件概率公式将两项结合，描述出该极大团中隐变量的条件分布：
  $$\mathcal{P}(i_t,i_{t+1}\mid \mathcal{O})=\mathcal{G}(i_t\mid \mathcal{O})\cdot \mathcal{Q}(i_{t+1}\mid i_t,\mathcal{O})$$

将所有极大团串联在一起，最终得到关于隐变量的条件概率密度函数$\mathcal{P}(\mathcal{I}\mid \mathcal{O})$。

向量角度描述条件概率(2022/11/13)

状态转移过程逻辑解释

继续观察线性条件随机场的条件概率表示$\mathcal{P}(\mathcal{I}\mid \mathcal{O})$：
$$\mathcal{P}(\mathcal{I}\mid \mathcal{O})=\frac{1}{\mathcal{Z}}\exp \left[\sum _{t=1}^{T-1}\sum _{m=1}^{\mathcal{M}}{\lambda }_m\cdot s_m(i_{t+1},i_t,\mathcal{O})+\sum _{t=1}^T\sum _{l=1}^{\mathcal{L}}{\eta }_l\cdot g_l(i_t,\mathcal{O})\right]$$
假设隐变量$i_t(t=1,2,\cdots ,T)$是 离散型随机变量：
$$i_t\in \mathcal{S}=\{s_1,s_2,\cdots ,s_{|\mathcal{S}|}\}$$
其中$|\mathcal{S}|$表示可选离散集合中可选的元素数量。而上式中$\mathcal{M}$表示隐状态$i_t$向$i_{t+1}$转移过程中可能性的数量。根据$|\mathcal{S}|$的描述，必然有：
例如：$i_t=s_1\to i_{t+1}=s_1$,以此类推。
$$\mathcal{M}\le |\mathcal{S}{|}^2$$
而这些排列组合，对应的转移特征函数$s_m(i_{t+1},i_t,\mathcal{O})$集合仅包含 两种结果：$0,1$。根据上述特征函数的定义，结果为$1$的状态转移过程是满足既定事实的，但即便这些组合满足条件，同样存在区分，而这些区分由模型参数${\lambda }_m$决定。

条件概率的简化过程

场景设计

实际上，$\mathcal{P}(\mathcal{I}\mid \mathcal{O})$中$\mathcal{I},\mathcal{O}$分别以关于隐变量与观测变量的向量形式出现：
$$\mathcal{I}=\left(\begin{array}{c}{i}_1\\ i_2\\ ⋮\\ i_T\end{array}\right),\mathcal{O}=\left(\begin{array}{c}{o}_1\\ o_2\\ ⋮\\ o_T\end{array}\right)$$
在条件随机场——背景介绍提到的最大熵模型中，归一化因子$\mathcal{Z}$是一个关于条件部分的函数。从上述的条件概率描述来看，$\mathcal{Z}$同样和模型参数存在关系：
注意：归一化函数$\mathcal{Z}$本身就是对后验$\mathcal{I}$进行归一化/积分，因此，$\mathcal{Z}$和$\mathcal{I}$无关。
因此，引入模型参数向量$\lambda ,\eta$：
$$\lambda ={\left(\begin{array}{c}{\lambda }_1\\ {\lambda }_2\\ ⋮\\ {\lambda }_{\mathcal{M}}\end{array}\right)}_{\mathcal{M}\times 1},\eta ={\left(\begin{array}{c}{\eta }_1\\ {\eta }_2\\ ⋮\\ {\eta }_{\mathcal{L}}\end{array}\right)}_{\mathcal{L}\times 1}$$
于此同时，为了消除${\sum }_{m=1}^{\mathcal{M}},{\sum }_{l=1}^{\mathcal{L}}$，并将其表示为向量的乘积形式，同样需要对 状态特征函数$g$和转移特征函数$s$ 进行向量表示：
$$s(i_{t+1},i_t,\mathcal{O})={\left(\begin{array}{c}{s}_1(i_{t+1},i_t,\mathcal{O})\\ s_2(i_{t+1},i_t,\mathcal{O})\\ ⋮\\ s_{\mathcal{M}}(i_{t+1},i_t,\mathcal{O})\end{array}\right)}_{\mathcal{M}\times 1},g(i_t,\mathcal{O})={\left(\begin{array}{c}{g}_1(i_t,\mathcal{O})\\ g_2(i_t,\mathcal{O})\\ ⋮\\ g_{\mathcal{L}}(i_t,\mathcal{O})\end{array}\right)}_{\mathcal{L}\times 1}$$

简化过程

• 在定义完上述向量后，对建模对象$\mathcal{P}(\mathcal{I}\mid \mathcal{O})$进行如下简化：
  将${\sum }_{m=1}^{\mathcal{M}},{\sum }_{l=1}^{\mathcal{L}}$用‘向量乘积’的方式表示。
  $$\mathcal{P}(\mathcal{I}\mid \mathcal{O})=\frac{1}{\mathcal{Z}(\mathcal{O},\lambda ,\eta )}\exp \left[\sum _{t=1}^{T-1}{\lambda }^{T}s(i_{t+1},i_t,\mathcal{O})+\sum _{t=1}^T{\eta }^{T}g(i_t,\mathcal{O})\right]$$

• 继续观察中括号中的项，以第一项${\sum }_{t=1}^{T-1}{\lambda }^{T}s(i_{t+1},i_t,\mathcal{O})$为例，假设将其展开，可能会得到如下形式：
  注意：不要将${\lambda }^T$中的'转置'$T$与表示时间/序列的$T$搞混~
  $$\begin{array}{rl}\sum _{t=1}^{T-1}{\lambda }^{T}s(i_{t+1},i_t,\mathcal{O})& ={\lambda }^{T}s(i_2,i_1,\mathcal{O})+{\lambda }^{T}s(i_3,i_2,\mathcal{O})+\cdots +{\lambda }^{T}s(i_T,i_{T-1},\mathcal{O})\\ & ={\lambda }^T\left[s(i_2,i_1,\mathcal{O})+s(i_3,i_2,\mathcal{O})+\cdots +s(i_T,i_{T-1},\mathcal{O})\right]\\ & ={\lambda }^T\sum _{t=1}^{T-1}s(i_{t+1},i_t,\mathcal{O})\end{array}$$
  同理，${\sum }_{t=1}^T{\eta }^{T}g(i_t,\mathcal{O})$也可以写成如下形式：
  $$\sum _{t=1}^T{\eta }^{T}g(i_t,\mathcal{O})={\eta }^T\sum _{t=1}^{T}g(i_t,\mathcal{O})$$
  此时，$\mathcal{P}(\mathcal{I}\mid \mathcal{O})$可化简为如下形式：
  $$\mathcal{P}(\mathcal{I}\mid \mathcal{O})=\frac{1}{\mathcal{Z}(\mathcal{O},\lambda ,\eta )}\exp \left[{\lambda }^T\sum _{t=1}^{T-1}s(i_{t+1},i_t,\mathcal{O})+{\eta }^T\sum _{t=1}^{T}g(i_t,\mathcal{O})\right]$$

• 继续观察中括号内的项，这种两项相乘再相加 的形式，同样可以继续化简称向量乘积的形式：
  定义 参数向量$\theta$，特征矩阵$\mathcal{H}(i_{t+1},i_t,\mathcal{O})$ 表示如下：
  由于$s(i_{t+1},i_t,\mathcal{O})$向量维度是$\mathcal{M}\times 1$，因此${\sum }_{t=1}^{T-1}s(i_{t+1},i_t,\mathcal{O})$的向量维度也是$\mathcal{M}\times 1$(向量对应元素相加)。同理，${\sum }_{t=1}^{T}g(i_t,\mathcal{O})$的向量维度是$\mathcal{L}\times 1$.
  $$\theta =\left(\begin{array}{c}\lambda \\ \eta \end{array}\right)={\left(\begin{array}{c}{\lambda }_1\\ ⋮\\ {\lambda }_{\mathcal{M}}\\ {\eta }_1\\ ⋮\\ {\eta }_{\mathcal{L}}\end{array}\right)}_{(\mathcal{M}+\mathcal{L})\times 1}\mathcal{H}(i_{t+1},i_t,\mathcal{O})={\left(\begin{array}{c}{\sum }_{t=1}^{T-1}s(i_{t+1},i_t,\mathcal{O})\\ \\ {\sum }_{t=1}^{T}g(i_t,\mathcal{O})\end{array}\right)}_{(\mathcal{M}+\mathcal{L})\times 1}$$

至此，将条件概率$\mathcal{P}(\mathcal{I}\mid \mathcal{O})$化简称如下向量乘积形式：
$$\begin{array}{rl}\mathcal{P}(\mathcal{I}\mid \mathcal{O})& =\frac{1}{\mathcal{Z}(\mathcal{O},\theta )}\exp \left[{\theta }^T\cdot \mathcal{H}(i_{t+1},i_t,\mathcal{O})\right]\\ & =\frac{1}{\mathcal{Z}(\mathcal{O},\theta )}\exp ⟨\theta ,\mathcal{H}(i_{t+1},i_t,\mathcal{O})⟩\end{array}$$

后续将使用$\mathcal{P}(\mathcal{I}\mid \mathcal{O})$的向量表示处理 学习以及推断任务。

相关参考：
最大熵模型（maximum entropy model）
(系列十七)条件随机场4-概率密度函数的参数形式
机器学习-条件随机场（5）-CRF模型-概率密度函数的向量形式
机器学习-周志华著