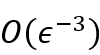一种逐样本的偏AUC优化框架
当前的深度神经网络已经在各种领域上取得了巨大的成功,常见的应用场景有图片分类、人脸识别、异常检测等。值得注意的是,深度学习的应用落地大多依赖于巨量且平衡的数据,然而现实生活中的大部分应用场景中,可用的数据大部分是服从某种长尾分布,即头部类和尾部类之间样本数目极度不平衡。因此,在实际工业应用中,如何在长尾数据上训练深度神经网络是目前亟需解决的问题。
接收者操作特征曲线(Receiver Operating Characteristic,在此简称为ROC)曲线是统计学中常用的模型性能衡量工具,其具体含义可以表示为在不同阈值下评分函数的真阳率(True Positive Rate,在此简称为TPR)与假阳率(False Positive Rate,在此简称为FPR)之间的关系。基于ROC曲线, 后续研究人员又提出接收者操作特征曲线下面积(Area Under the Receiver Operating Characteristic,在此简称为AUC)作为评价指标,即ROC曲线下夹面积来表示一个分类器在不平衡数据上的性能。大量研究表明AUC对数据分布不敏感[1][3][4],因此,AUC相比于准确率更加适合于衡量分类器在长尾分布数据上的性能。
相比于传统的不平衡数据分类问题,如医学诊断、垃圾邮件过滤以及风险金融账户检测等问题的应用场景中,往往更倾向于训练模型在较低的假阳率区间内获得更高的真阳率,换言之,这些应用场景更加关注于难样本的学习,而目前常用的AUC指标更关注于整体的表现,与现有需求不一致。因此,本文考虑优化模型在较低假阳率区间内的单路偏AUC指标,称为OPAUC,和较低假阳率和较高真阳率区间内的双路偏AUC指标,称为TPAUC。
本文采用现有的一种逐样本的AUC优化等价形式,结合可微分的替代优化损失ATK loss (Average Top-k Loss),提出偏AUC指标的一种非凸强凹minimax的渐进无偏重构形式,该重构形式可适用于单路偏AUC和双路偏AUC优化。结合目前最前沿的minimax优化技术,采用本文所提出的重构形式,单路偏AUC和双路偏AUC优化与随机梯度下降算法具有相同的收敛速率
同时,为证明该框架的泛化能力,本文对该框架的泛化性进行了分析,使其具有良好的理论保证。
论文标题
Asymptotically Unbiased Instance-wise Regularized
Partial AUC Optimization: Theory and Algorithm
论文链接
https://arxiv.org/abs/2210.03967
论文来源
NeruIPS 2022
ROC曲线是统计学中常用的模型性能衡量工具,其具体含义可以表示为在不同阈值下评分函数的真阳率与假阳率之间的关系。基于ROC曲线, 后续研究人员又提出AUC作为评价指标,即ROC曲线下夹面积来表示一个分类器在不平衡数据上的性能。研究人员已经证明AUC对数据分布不敏感,因此,AUC相比于准确率更加适合于衡量分类器在长尾分布数据上的性能。
从2000年起,AUC优化问题已经在机器学习社区中引起越来越高的关注。在过去的二十年里,关于AUC优化的研究已经从最简单的线性模型和决策树发展到最先进的深度学习架构。在深度学习的帮助下,人们现在可以很容易地应用AUC优化来处理各种现实世界的问题,例如金融欺诈检测、垃圾邮件检测到医疗诊断等等。
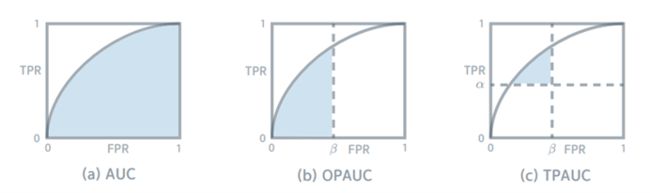
图1:不同AUC指标的变体。(a)标准AUC指标;(b)单路偏AUC(OPAUC);(c)双路偏AUC(TPAUC)。
然而,在长尾数据场景中,本文往往只对ROC曲线中的一个特定区域感兴趣,该区域下包围的面积被称为偏AUC(PAUC)。其中,单路偏AUC(OPAUC)衡量指定假阳率区间内的面积(0≤FPR≤β,0<β<1);而双路偏AUC(TPAUC)衡量指定假阳率和指定真阳率区间内的面积(α≤TPR≤1,0≤FPR≤β,0<α,β<1)。
与普通的AUC指标不同,优化偏AUC需要选择得分排名靠前或得分排名靠后的实例,从而导致了偏AUC优化是一个十分困难的组合优化问题。尽管近些年来涌现了一些研究去解决该问题。然而,这些研究中,大多数工作都依赖于确定性数据优化(每次迭代都需要计算全部样本数据)和样本得分排序近似的技巧,这使得现有的算法存在着较大的偏差和较低的效率。
最近,研究人员开始探索深度学习模型的随机小批量数据的偏AUC优化, 提出了一种新颖的端到端的偏AUC优化框架。这种新型的重构方式在随机优化算法的帮助下具有较快的收敛率,但该方法对偏AUC的估计仍有一定偏差。最先进的深度学习架构提出了一种分布式鲁棒优化(Distributionary Robust Optimization,简称为DRO)的偏AUC优化框架,通过巧妙的重构形式和复合式随机梯度下降算法可以消除偏差。然而,关于最先进的深度学习架构文献中采用的是逐对的损失函数,逐对的损失函数在样本量方面的可扩展性有限,对于单路偏AUC优化的收敛率与普通随机梯度下降的收敛率保持一致,而双路偏AUC优化的收敛率会明显变慢。
首次以提出指定FPR区间内的端到端的单路偏AUC优化框架,然而,该算法并不适用于双路偏AUC优化。因此,本文提出一种更加适合于端到端的学习方式的逐样本偏AUC优化框架解决现有的优化困难问题。
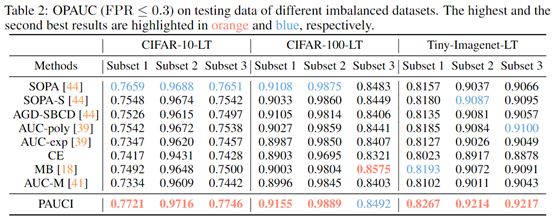
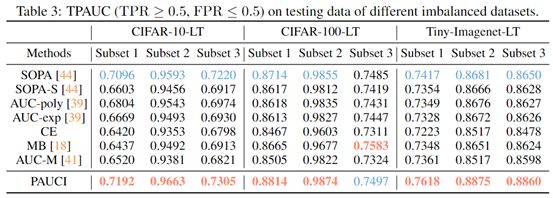
本文分别对OPAUC和TPAUC在多个数据集上进行了一系列实验。本文采用了三个图片分类数据集并分别构造了相对应的不平衡的二分类数据集:CIFAR-10-LT,CIFAR-100-LT和Tiny-ImageNet-200-LT,其中二分类数据集的构造方式是选择一个超类作为正类,其余类别作为负类。
从表2和表3中,可以观察到如下结果:
(1)本文所提出的方法PAUCI在大多数实验中表现要优于其他对比方法。即使是在PAUCI表现最差的实验中,该方法仍然比表现最好的算法相差不大。
(2)除此之外,很容易看出普通的AUC优化算法AUC-M在PAUC优化场景中表现并不好,这表明了研究高效的PAUC优化算法是有必要的。(3)使用近似的优化算法SOPA-S,AUC-poly和AUC-exp比无偏算法SOPA和我们提出的PAUCI算法的表现要差一些。这表明之前使用的近似优化算法的性能较差,无偏的高效PAUC优化算法仍然是值得研究的热点。
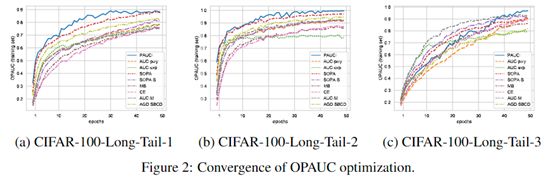
本文对不同方法在训练集上的收敛速度进行了实验,为了实验的公平性,所有算法均未使用二阶段训练方法,最优参数采用性能实验中所使用的参数,具体收敛实验结果如下图所示。
根据表2和表3,可以得到以下结论:
(1)本文所提出的方法与SOPA算法在OPAUC优化实验中收敛速度要快于其他方法。然而,对于TPAUC优化实验来说,由于其算法的复杂性,SOPA收敛速度明显变慢。本文所提方法仍然具有较快的收敛速度。(2)值得注意的是,本文所提方法在前20轮迭代后就趋近于收敛状态,这表明该方法具有较好的稳定性。
本文主要的贡献点在于为PAUC设计一种高效且渐进无偏的优化方法。本文首先为OPAUC和TPAUC提出了一个非凸强凹的minimax 逐样本的优化框架。使用这种方式,将头部难样本选择过程纳入损失计算中,以消除排序操作带来的问题。对于OPAUC和TPAUC的优化问题,本文采用了一种高效的随机最小化算法,确保能够在
次迭代后找到一个ϵ-鞍点。此外,本文还提出了对目标函数的泛化误差的理论分析,该结论可能有助于未来关于AUC泛化的工作。最后,一系列不平衡的二分类数据集的实验说明了本文所提方法的有效性。