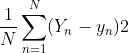Linear Model(Exhaustive method 穷举法)
目录
1. Assignment
2. Function Set
3. Loss Function
4. Exhaustive method
5. Code
学习内容来自:b站的刘二大人----《PyTorch深度学习实践》
1. Assignment
利用简单的线性模型实现对输入x的预测
假设我们的Training set是
| x | y(hat) |
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
其中应该还有一个x = 4,y =?作为我们的测试集(Test set)
如果这里的y是可以看见的话,那么在训练模型的时候可能会根据测试集进行调整。那么,测试集就会失去本来的意义。相当于,想用训练好的模型去预测新的x,但是我们想要预测的x已经成为训练集的一部分了,那么预测就变得没有意义了。
2. Function Set
其实,所谓的模型就是一个函数 f ,也可以说是一个函数集 function set
假如模型是一个线性的函数,y = kx+b
我们知道,决定一个二维的线性函数只需要两个参数k、b,也就是斜率和截距。如果当k和b取值不一样的时候,函数的样子就会变得不一样。也就是说k和b取遍实数集的时候,函数y可以覆盖整个的二维平面。那么这里所有的函数y就是一个函数集,也就是我们的所有模型的可能
最后根据我们的需要,选择最合适的那个k、b,选取一个特定的函数y,就是我们需要的模型
这里我们先用简单的线性模型去实现我们的问题,所有的问题都可以尝试这样的思路去解决。毕竟能用高中的知识解决,绝不用大学的方法去实现。当简单的线性模型无法解决问题的时候,再去考虑复杂的模型
这里我们采用线性模型:y = w * x(这里w代表斜率)
根据不同的k,可以画出不同的函数曲线,需要找到最好的函数
如果我们的函数能够最大化的适应我们的训练集(能够最大化的经过我们这些点),就认为是最好的函数
3. Loss Function
虽然这篇文章的所解决的问题比较简单,但对于实际的问题,往往是看不出真正好的函数的。
所以解决的办法是,先设定一个初始值w,然后就可以画出一个函数。这样,计算出我们的预测值y(y hat ,习惯将预测值y,或者说我们模型输出的那个值用y hat表示)与实际值的差,然后计算差的平方(类似与方差中波动程度的概念)来定义这个函数有多不好
这里就是损失函数Loss function
Y 代表 y hat 预测值
- Loss 损失函数:对应的是一个样本
- Cost 成本函数:对应的是整个样本,也就是Training Set
Loss 损失函数代表的意思是这个函数有多不好,从数学公式上也可以看出来,它代表的是预测值与真实值的差,平方是为了保证 y >= 0 ,所以Loss 应该越小越好
这里采用的是MSE(Mean Square Error)均方差的公式
计算MSE:
4. Exhaustive method
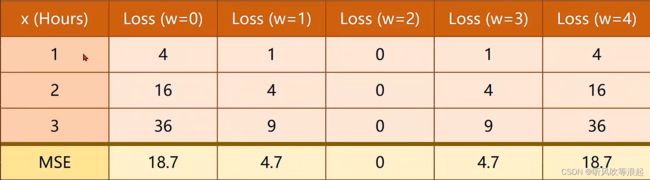
本篇文章采用穷举法来实现,通过观察,发现w在【0,4】区间上比较合适
穷举法:列出所有的可能情况,找出符合条件的情况
5. Code
穷举法代码实现:
import numpy as np
import matplotlib.pyplot as plt
x_date = [1.0,2.0,3.0]
y_date = [2.0,4.0,6.0]
def forward(x):
return x * w
def loss(x,y):
y_pred = forward(x)
return (y_pred - y) * (y_pred - y)
w_list = []
mse_list = []
for w in np.arange(0.0,4.1,0.1):
print('w=',w)
l_sum = 0
for x_val,y_val in zip(x_date,y_date):
y_pred_val = forward(x_val)
loss_val = loss(x_val,y_val)
l_sum += loss_val
print('\t',x_val,y_val,y_pred_val,loss_val)
print('MSE=',l_sum/3)
w_list.append(w)
mse_list.append(l_sum/3)
plt.plot(w_list,mse_list)
plt.xlabel('w')
plt.ylabel('Cost')
plt.show()1.定义 Training Set 训练集x,y
2. 定义函数,输入x,通过函数输出预测值,深度学习里这一过程叫前向传播
3. 定义loss函数,预测值与真实值差的平方
4. 利用穷举法,将w从0到4之间的情况列出,这里间距为0.1
zip 打包函数,将x,y对应成分打包
代码输出的部分展示:
画图结果为: