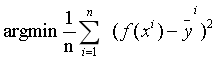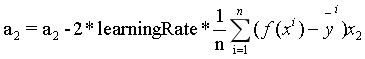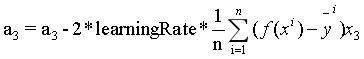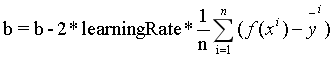梯度下降 java_梯度下降法求多元线性回归及Java实现
对于数据分析而言,我们总是极力找数学模型来描述数据发生的规律, 有的数据我们在二维空间就可以描述,有的数据则需要映射到更高维的空间。数据表现出来的分布可能是完全离散的,也可能是聚集成堆的,那么机器学习的任务就是让计算机自己在数据中学习到数据的规律。那么这个规律通常是可以用一些函数来描述,函数可能是线性的,也可能是非线性的,怎么找到这些函数,是机器学习的首要问题。
本篇博客尝试用梯度下降法,找到线性函数的参数,来拟合一个数据集。
假设我们有如下函数
![]() ,其中x是一个三个维度,
,其中x是一个三个维度,
![]()
写一个java程序来,随机产生100笔数据作为训练集。Random random = new Random();
double[] results = new double[100];
double[][] features = new double[100][3];
for (int i = 0; i < 100; i++) {
for (int j = 0; j < features[i].length; j++) {
features[i][j] = random.nextDouble();
}
results[i] = 3 * features[i][0] + 4 * features[i][1] + 5 * features[i][2] + 10;
} 上面的程序中results就是函数的值,features的第二维就是随机产生的3个x。
有了训练集,我们的任务就变成了如何求出3个各种的系数3、4、5,以及偏移量10,系数和偏移量可以取任意值,那么我们就得到了一个函数集,任务转化一下就变成了找出一个函数作用于训练集之后,与真实值的误差最小,如何评判误差的大小呢?我们需要定义一个函数来评判,那么给这个函数取一个名字,叫损失函数。这里,损失函数定义为
![]() 为真实值,问题就转化为在训练集中求如下函数:
为真实值,问题就转化为在训练集中求如下函数:
如何求这个函数的极小值呢?如果我们计算能力无限大,直接穷举就完了,但是这不是高效的办法,这时候就说的了梯度下降法,我们来看看数学里对梯度的定义。
在微积分里面,对多元函数的参数求∂偏导数,把求得的各个参数的偏导数以向量的形式写出来,就是梯度。比如函数f(x,y), 分别对x,y求偏导数,求得的梯度向量就是(∂f/∂x, ∂f/∂y)T,简称grad f(x,y)或者▽f(x,y)。
梯度告诉我们两件事情:
1、函数增大的方向
2、我们走向增大的方向,应该走多大步幅
求极小值,我们反方向走即可,加个负号,但是这个步幅有个问题,如果过大,参数就直接飞出去了,就很难在找到最小值,如果太小,则很有可能卡在局部极小值的地方。所以,我们设计了一个系数来调节步幅,我们叫它学习速率learningRate。
好了,为了好描述,我们把上面的函数泛化一下,表示成如下公式:
![]()
损失函数对每个参数求偏导数,根据偏导数值,当然求导的过程需要用到链式法则,,这里我们直接给出参数更新公式如下:
对于BGD(批量梯度下降法):
对于SGD(随机梯度下降法),SGD与BGD不同的是每笔数据,我们都更新一次参数,效率比较低下。公式和上面类似,去掉求和符号和除以N即可。
下面是具体的代码实现
import java.util.Random;
public class LinearRegression {
public static void main(String[] args) {
// y=3*x1+4*x2+5*x3+10
Random random = new Random();
double[] results = new double[100];
double[][] features = new double[100][3];
for (int i = 0; i < 100; i++) {
for (int j = 0; j < features[i].length; j++) {
features[i][j] = random.nextDouble();
}
results[i] = 3 * features[i][0] + 4 * features[i][1] + 5 * features[i][2] + 10;
}
double[] parameters = new double[] { 1.0, 1.0, 1.0, 1.0 };
double learningRate = 0.01;
for (int i = 0; i < 30; i++) {
SGD(features, results, learningRate, parameters);
}
parameters = new double[] { 1.0, 1.0, 1.0, 1.0 };
System.out.println("==========================");
for (int i = 0; i < 3000; i++) {
BGD(features, results, learningRate, parameters);
}
}
private static void SGD(double[][] features, double[] results, double learningRate, double[] parameters) {
for (int j = 0; j < results.length; j++) {
double gradient = (parameters[0] * features[j][0] + parameters[1] * features[j][1]
+ parameters[2] * features[j][2] + parameters[3] - results[j]) * features[j][0];
parameters[0] = parameters[0] - 2 * learningRate * gradient;
gradient = (parameters[0] * features[j][0] + parameters[1] * features[j][1] + parameters[2] * features[j][2]
+ parameters[3] - results[j]) * features[j][1];
parameters[1] = parameters[1] - 2 * learningRate * gradient;
gradient = (parameters[0] * features[j][0] + parameters[1] * features[j][1] + parameters[2] * features[j][2]
+ parameters[3] - results[j]) * features[j][2];
parameters[2] = parameters[2] - 2 * learningRate * gradient;
gradient = (parameters[0] * features[j][0] + parameters[1] * features[j][1] + parameters[2] * features[j][2]
+ parameters[3] - results[j]);
parameters[3] = parameters[3] - 2 * learningRate * gradient;
}
double totalLoss = 0;
for (int j = 0; j < results.length; j++) {
totalLoss = totalLoss + Math.pow((parameters[0] * features[j][0] + parameters[1] * features[j][1]
+ parameters[2] * features[j][2] + parameters[3] - results[j]), 2);
}
System.out.println(parameters[0] + " " + parameters[1] + " " + parameters[2] + " " + parameters[3]);
System.out.println("totalLoss:" + totalLoss);
}
private static void BGD(double[][] features, double[] results, double learningRate, double[] parameters) {
double sum = 0;
for (int j = 0; j < results.length; j++) {
sum = sum + (parameters[0] * features[j][0] + parameters[1] * features[j][1]
+ parameters[2] * features[j][2] + parameters[3] - results[j]) * features[j][0];
}
double updateValue = 2 * learningRate * sum / results.length;
parameters[0] = parameters[0] - updateValue;
sum = 0;
for (int j = 0; j < results.length; j++) {
sum = sum + (parameters[0] * features[j][0] + parameters[1] * features[j][1]
+ parameters[2] * features[j][2] + parameters[3] - results[j]) * features[j][1];
}
updateValue = 2 * learningRate * sum / results.length;
parameters[1] = parameters[1] - updateValue;
sum = 0;
for (int j = 0; j < results.length; j++) {
sum = sum + (parameters[0] * features[j][0] + parameters[1] * features[j][1]
+ parameters[2] * features[j][2] + parameters[3] - results[j]) * features[j][2];
}
updateValue = 2 * learningRate * sum / results.length;
parameters[2] = parameters[2] - updateValue;
sum = 0;
for (int j = 0; j < results.length; j++) {
sum = sum + (parameters[0] * features[j][0] + parameters[1] * features[j][1]
+ parameters[2] * features[j][2] + parameters[3] - results[j]);
}
updateValue = 2 * learningRate * sum / results.length;
parameters[3] = parameters[3] - updateValue;
double totalLoss = 0;
for (int j = 0; j < results.length; j++) {
totalLoss = totalLoss + Math.pow((parameters[0] * features[j][0] + parameters[1] * features[j][1]
+ parameters[2] * features[j][2] + parameters[3] - results[j]), 2);
}
System.out.println(parameters[0] + " " + parameters[1] + " " + parameters[2] + " " + parameters[3]);
System.out.println("totalLoss:" + totalLoss);
}
}
运行结果如下:
同样是更新3000次参数。
1、SGD结果:
参数分别为:3.087332784857909 、4.075233812033048 、5.06020828348889、 9.89116046652793
totalLoss:0.13515381461776949
2、BGD结果:
参数分别为:3.0819123489025344 、4.064145151461403、5.046862571520019、 9.899847277313173
totalLoss:0.1050937019067582
可以看出,BGD有更好的表现。
快乐源于分享。
此博客乃作者原创, 转载请注明出处