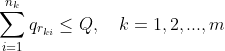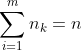matlab遗传算法求解车辆路径问题（一）
一、引言
本文将结合知网论文《车辆路径问题的改进遗传算法》，并参考南柯一梦的文章和代码对模型进行复现，并尝试探讨如何在遗传算法中用代码对模型的目标函数和约束条件进行刻画。
二、问题描述
设物流中心有m辆配送车辆，载重量为Q，需要向n个客户送货，每个客户的货物需求量为
，客户到客户的距离里为
，物流中心到各客户的距离为
。再设
为第k辆车配送的客户数（
表示未使用第k台车辆），用集合
表示第k条路径，也即第k辆车走的路径，其中元素
表示第个客户在路径k中的顺序为i（不包括物流中心）。令
表示物流中心，若以配送总里程最短为目标函数，则可建立物流配送车辆路径问题的数学模型：
![Min Z=\sum_{k=1}^{m}[\sum_{i=1}^{n_k}d_{r_{k(i-1)}r_{ki}}+d_{r_kn_k}sign(n_k)]](http://img.e-com-net.com/image/info8/2a570ce3e684461a954630171b7f5eff.gif)
（1）
（2）
（3）
（4）
（5）
（6）
（7）
三、算法思路分析
对目标函数和约束的详细解释可以参见原文，模型比较简单，这里主要强调的是遗传算法的编码思路。原文中有两点可取的地方值得参考：（1）考虑存在m-1个虚拟配送中心，并将虚拟配送中心加入到种群的个体中。这样做的好处是，在初始生成随机个体的时候同时也生成了相应的车辆配送路径。（2）对存在超出约束范围的路径的个体赋予距离惩罚，这样在对种群进行筛选时被惩罚的个体总路径会明显大于可行个体，因而容易被淘汰。
文中比较不可取的地方为对种群可行化的过程，具体的可行化步骤写得极为复杂，而且还有很多错误。前四步简而言之就是找到个体中的不同路径，并对路径载重大于限额的车辆进行标记。标记完后，对超载路径进行客户的转移。如果该路径不是个体中的最后一个路径，则客户转移给下一个路径。如果是最后一个路径，转移给第一个路径，直到所有的路径都复合条件。
强烈不建议大家对这个可行化过程进行代码编写，十分费劲。我尝试编写了只包含两个车辆的可行化过程代码，最终的结果比原文（67.5km）和南柯一梦（67km）的结果要差一点，为（68km）。这里需要注意的是，南柯一梦的模型中，对第四个需求点的重量赋值为2t，如果改成原文的0t，就可以得到67km的最优解。我编写的可行化过程的代码十分臭长，就不放在这里了。
但仔细思考一下原文和南柯一梦decode（尽管思路清晰而且代码干净）的算法思路，感觉在求最优解的地方还是有欠缺的地方。当然我水平有限，现在也想不出来。不过我用最简单的遗传算法的思路结合南柯一梦的代码，发现确实能得到更优的结果（65.5km），在这里进行一下展示。
四、GA代码
4.1交叉
交叉的部分直接引用南柯一梦的代码，首先是配对函数：
function [new_pop_intercross]=Mating_pool(population_num,population,Pc)
%%
%输入:population,population_num,Pc
%输出：1.new_popopulation_intercross
% 2.c3，配对池：随机将种群population两两配对
% 3.pool
%%
pl=randperm(population_num); % 将种群打散用于配对
num=population_num/2;
c3=zeros(2,num);
pool=[];
new_pop_intercross=population;
for kj=1:num
c3(1,kj)=pl(2*kj-1);
c3(2,kj)=pl(2*kj);
end %生成"配对池c3
%%判断“配对池c3”每一对个体的随机数是否小于交叉概率Pc
rd=rand(1,num);
for kj=1:num
if rd(kj)其次是两个个体的交叉函数，我对VRP的算法思路稍作了解释，详见代码注释：
% 因为VRP问题中的一个重要约束是要遍历需求点，且每个点只访问一次，所以A，B两个染色体配对成功后
% 首先要确定交叉的基因段，选择好后先对染色体A进行交叉操作，清楚A中交叉基因段，在B中找到A中被
% 清除的需求点的位置，去除B中其余的需求点，将剩余的需求点直接插入A中的交叉基因段，这样就保证了
% 染色体A仍然遍历所有的需求点且每个需求点只经过一次
function [A,B]=cross(A,B)
A_1=A;
B_1=B;
r=randperm(length(A));
c=min(r(1,1:2));
d=max(r(1,1:2));
for i=c:d
A(i)=0;
end
B_1(ismember(B_1,A))=[];
A(1,c:d)=B_1;
for i=c:d
B(i)=0;
end
A_1(ismember(A_1,B))=[];
B(1,c:d)=A_1;
end4.2 变异
变异后的种群规模大概率比原来的种群大
function [Mut_Pop]=Mutation(Cross_Pop,Pm)
Mut_Pop=Cross_Pop;
Cross_Pop_num=size(Cross_Pop,1);
for j=1:Cross_Pop_num
A=Cross_Pop(j,:); % 要进行变异的染色体
A_1=A; % 对A进行记录，之后交换变异需求点的时候要用到
n=size(A,2);
r=rand(1,n);
Pe=find(r4.3选择
% 计算每个个体中所有车辆的载重和距离，如果个体中存在车辆的载重或者距离超过要求，增加惩罚函数
% 输入：种群pop，车辆数m，距离矩阵D，配送中心距离X，各点需求Demand,距离上限dis_max,重量上限cap_max
% 输出：个体总距离，总重量
function [lenPop,weightPop] = resultLW(pop,m,D,Demand,dis_max,cap_max)
[indNum,customerNum] = size(pop);
cenIndicate = randperm(customerNum-m+1);
lenPop=zeros(indNum,m); % 记录个体总路径距离
weightPop=zeros(indNum,m); % 记录个体总重量
for i = 1:m-1
cenIndicate = [cenIndicate 0]; % 这里只包含需求点的编码，虚拟配送中心为0
end
for i = 1:indNum
lVirCen = find(ismember(pop(i,:),cenIndicate)==0); % 对虚拟配送中心进行标记
for j = 1:m
if j==1
a=pop(i,:);
p=[a(lVirCen(1)) a(1:lVirCen(1))];
p1=p(1:end-1);
p2=p(2:end);
lenPop(i,1)=sum(D((p1-1)*customerNum+p2)); % 求出该路径的总长度，这里将矩阵D按行展开
weightPop(i,1)=sum(Demand(p));
if lenPop(i,1) > dis_max
lenPop(i,1) = lenPop(i,1) + 500;
end
if weightPop(i,1) > cap_max
lenPop(i,1) = lenPop(i,1) + 500;
end
elseif j==m
a=pop(i,:);
p=[a(lVirCen(m-1):customerNum) a(lVirCen(m-1))];
p1=p(1:end-1);
p2=p(2:end);
lenPop(i,j)=sum(D((p1-1)*customerNum+p2));
weightPop(i,j)=sum(Demand(p));
if lenPop(i,j) > dis_max
lenPop(i,j) = lenPop(i,j) + 500;
end
if weightPop(i,j) > cap_max
lenPop(i,j) = lenPop(i,j) + 500;
end
else
a=pop(i,:);
p=[a(lVirCen(j-1):lVirCen(j))];
p1=p(1:end-1);
p2=p(2:end);
lenPop(i,j)=sum(D((p1-1)*customerNum+p2));
weightPop(i,j)=sum(Demand(p));
if lenPop(i,j) > dis_max
lenPop(i,j) = lenPop(i,j) + 500;
end
if weightPop(i,j) > cap_max
lenPop(i,j) = lenPop(i,j) + 500;
end
end
end
end这里的resultLW函数是在对种群进行交叉和变异操作后执行，返回的值为种群中每个个体的总路径长度和总重量（总重量其实用不到）。思路很简单，先找到每个个体中的虚拟配送中心，然后对个体中的每个路径的距离和载重进行计算，超过约束条件的路径就对其进行惩罚。
4.4主函数
clc
clear
close all;
tic;
%%
%算法参数
population_num=80;%种群规模
Max_gen=200;%迭代次数
Pc=0.8;%交叉概率
Pm=0.05;%变异概率
%%
%问题参数
%车辆数量Car_num=2
%客户数量Customer_num=8
%车辆容量capacity_max=8
%行驶距离distance_max=50
Car_num=2;
Customer_num=8;
capacity_max=8;
distance_max=50;
load Demand %客户的需求
load Distance %客户间的距离
load X %物流中心到客户间的距离
%%
%种群初始化
population=zeros(population_num,Customer_num + Car_num - 1);
for i=1:population_num
population(i,:)=randperm(Customer_num + Car_num - 1); % 产生含有虚拟配送中心的随机个体
end
%%
for i = 1:Car_num-1 % 这里需要对Demand X 和Distance的数据进行更新
Demand = [Demand 0];
X = [X 0];
Distance = [Distance X(1:end-1)'];
Distance = [Distance; X];
end
y=1;%循环计数器
while y五、算例展示
实例1：某物流中心有2台配送车辆，其载重量均为8t，车辆每次配送的最大行驶距离为50Km，配送中心(编号为0)与8个客户之间及8个客户相互之间的距离dij、8个客户的货物需求量qj (i, j=1,2,…,8) 见下表1。要求合理安排车辆配送路线，使配送总里程最短。
| 客户 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 0 | 0 | 4 | 6 | 7.5 | 9 | 20 | 10 | 16 | 8 |
| 1 | 4 | 0 | 6.5 | 4 | 10 | 5 | 7.5 | 11 | 10 |
| 2 | 6 | 6.5 | 0 | 7.5 | 10 | 10 | 7.5 | 7.5 | 7.5 |
| 3 | 7.5 | 4 | 7.5 | 0 | 10 | 5 | 9 | 9 | 15 |
| 4 | 9 | 10 | 10 | 10 | 0 | 10 | 7.5 | 7.5 | 10 |
| 5 | 20 | 5 | 10 | 5 | 10 | 0 | 7 | 9 | 7.5 |
| 6 | 10 | 7.5 | 7.5 | 9 | 7.5 | 7 | 0 | 7 | 10 |
| 7 | 16 | 11 | 7.5 | 9 | 7.5 | 9 | 7 | 0 | 10 |
| 8 | 8 | 10 | 7.5 | 15 | 10 | 7.5 | 10 | 10 | 0 |
| 需求量 | 0 | 1 | 2 | 1 | 0 | 1 | 4 | 2 | 2 |
这个模型的平均表现不如南柯一梦的代码，但多实验几次能找到更优的配送方案，车辆1路径为0-4-6-7-2-0车辆2路径为0-8-5-3-1-0，总路径为65.5km。
参考文献
[1] 遗传算法求解车辆路径问题 - 知乎
[2] 封全喜,刘诚,贾贞.车辆路径问题的改进遗传算法[J].数学的实践与认识,2008(13):123-129.