李宏毅 self-attention

https://unclestrong.github.io/DeepLearning_LHY21_Notes/Notes_html/10_Self-attention_P1.html

解决的问题：输入的长度不固定

怎么表示么？
one-hot向量法
word-enbedding

还有图网络，音频网络，

一整个输入，一堆输出
一整个输入，一个输出

请看作业五 seq2seq

存在问题：对于同样的单词，词性没法分析，因为同一个单词丢进去，他给的结果应该是一样的。

有没有更好的方法,来考虑整个Input Sequence的资讯呢,

Self-Attention

Self-Attention的运作方式就是,Self-Attention会吃一整个Sequence的资讯

然后你Input几个Vector,它就输出几个Vector,这4个Vector,他们都是考虑一整个Sequence以后才得到的

可以把Fully-Connected的Network,跟Self-Attention交替使用

那Self-Attention是怎麼运作的呢

Self-Attention过程

Self-Attention的Input,它就是一串的Vector

这里有一个特别的机制,这个机制是根据这个向量,找出整个很长的sequence裡面,到底哪些部分是重要的,哪些部分跟判断是哪一个label是有关係的,哪些部分是我们要决定的class,决定的regression数值的时候,所需要用到的资讯

每一个向量跟的关联的程度,用一个数值叫α来表示

这个self-attention的module,怎麼自动决定两个向量之间的关联性呢,你给它两个向量跟,它怎麼决定跟有多相关,然后给它一个数值α呢,那这边呢你就需要一个计算attention的模组

这个计算attention的模组,就是拿两个向量作為输入,然后它就直接输出α那个数值,

这个计算attention的模组,就是拿两个向量作為输入,然后它就直接输出α那个数值,

计算这个α的数值有各种不同的做法

• 比较常见的做法呢,叫做用dot product,输入的这两个向量分别乘上两个不同的矩阵,左边这个向量乘上$W^q$这个矩阵得到矩阵q,右边这个向量乘上$W^k$这个矩阵得到矩阵k
• 再把q跟k做dot product,就是把他们做element-wise 的相乘,再全部加起来以后就得到一个 scalar,这个scalar就是α,这是一种计算α的方式

有另外一个叫做Additive的计算方式,它的计算方法就是,把同样这两个向量通过 ,得到跟,那我们不是把它做Dot-Product(点积),是把它这个串起来,然后丢到这个过一个Activation Function

然后再通过一个Transform,然后得到α

总之有非常多不同的方法,可以计算Attention,可以计算这个α的数值,可以计算这个关联的程度

但是在接下来的讨论裡面,我们都只用左边这个方法,这也是今日最常用的方法,也是用在Transformer裡面的方法

你把$a^1$乘上$W^q$得到$q^1$,那这个q有一个名字,我们叫做Query,它就像是你搜寻引擎的时候,去搜寻相关文章的问题,就像搜寻相关文章的关键字,所以这边叫做Query

Wq应该是随机初始化然后再随网络一起训练的

然后接下来呢,你都要去把$a^2$,$a^3$$a^4$它乘上$W^k$,得到k这个Vector,这个Vector叫做Key,那你把这个Query q1,跟这个Key k2,算Inner-Product就得到α

我们这边用$a_{1,2}$来代表说,Query是1提供的,Key是2提供的时候,这个1跟2他们之间的关联性,这个α这个关联性叫做Attention的Score,叫做Attention的分数,

W都是共享参数的

这个Soft-Max跟分类的时候的那个Soft-Max是一模一样的,所以Soft-Max的输出就是一排α,所以本来有一排α,通过Soft-Max就得到${\alpha }^{\prime }$

接下来得到这个${\alpha }^{\prime }$以后,我们就要根据这个${\alpha }^{\prime }$去抽取出这个Sequence裡面重要的资讯,根据这个α我们已经知道说,哪些向量跟是最有关係的,怎麼抽取重要的资讯呢,

• 首先把到$a^1$$a^2$$a^3$$a^4$这边每一个向量,乘上$W^v$得到新的向量,这边分别就是用$v^1$-----$v^4$来表示
• 接下来把这边的$v^1$-----$v^4$,每一个向量都去乘上Attention的分数,都去乘上${\alpha }^{\prime }$
• 然后再把它加起来,得到$b^1$
  

如果某一个向量它得到的分数越高,比如说如果$a^1$跟$a^2$的关联性很强,这个得到的${\alpha }^{\prime }$值很大,那我们今天在做Weighted Sum以后,得到的的$b^1$值,就可能会比较接近$v^2$
所以谁的那个Attention的分数最大,谁的v那个就会Dominant你抽出来的结果

所以这边呢我们就讲了怎麼从一整个Sequence 得到$b^1$

矩阵的角度

接下来我们从矩阵乘法的角度,再重新讲一次我们刚才讲的,Self-attention 是怎麼运作的

我们现在已经知道每一个 a 都產生 q k v

就是我们每一个 a,都乘上一个矩阵 $W^q$,得到 $q^i$,然后不同的a合并起来

W矩阵当然是用梯度下降train出来的

下面的K,V同理。四个拼起来叫Q和I

所以每一个 a 得到 q k v ,其实就是把输入的这个,vector sequence 乘上三个不同的矩阵,你就得到了 q,得到了 k,跟得到了 v

因为q，k形状相同，转置后才能向量乘法，相当于一个行向量和一个列向量相乘，得到了一个数值，就是我们的attention分数

那这个四个步骤的操作,你其实可以把它拼起来,看作是矩阵跟向量相乘

这四个动作,你可以看作是我们把$k^1$ 到 $k^4$ 拼起来,当作是一个矩阵的四个 row

那我们刚才讲过说,我们不只是$q^1$ ,要对$k^1$ 到 $k^4$ 计算 attention,$q^2,q^3,q^4$也要对$k^1$ 到 $k^4$ 计算 attention,操作其实都是一模一样的

所以这些 attention 的分数可以看作是两个矩阵的相乘,一个矩阵它的 row,就是$k^1$ 到 $k^4$,另外一个矩阵它的 column

所以现在这个矩阵A里面就是我们存储的Q跟V的attention的分数

我们会在 attention 的分数,做一下 normalization,比如说你会做 softmax,你会对这边的每一个 column,每一个 column 做 softmax,让每一个 column 裡面的值相加是 1

通过了 softmax 以后,它得到的值有点不一样了,所以我们用 ,来表示通过 softmax 以后的结果$A^{\prime }$

你就把$v^1$ 到 $v^4$拼起来,你把$v^1$ 到 $v^4$当成是V 这个矩阵的四个 column,把它拼起来,然后接下来你把 v 乘上$A^{\prime }$, 的第一个 column 以后,你得到的结果就是 $b^1$

,得到 O 这个矩阵,O 这个矩阵裡面的每一个 column,就是 Self-attention 的输出,也就是$b^1$ 到 $b^4$

整个过程

• I 是 Self-attention 的 input,Self-attention 的 input 是一排的vector,这排 vector 拼起来当作矩阵的 column,就是 I
• 这个 input 分别乘上三个矩阵$W^q{W}^k{W}^v$, 得到 Q K V
• 这三个矩阵,接下来 Q 乘上 K 的 transpose,得到 A 这个矩阵,A 的矩阵你可能会做一些处理,得到$A^{\prime }$ ,那有时候我们会把这个$A^{\prime }$ ,叫做 Attention Matrix，生成Q矩阵就是为了得到Attention的score
• 然后接下来你把个$A^{\prime }$ 再乘上 V,就得到 O,O 就是 Self-attention 这个 layer 的输出,生成V是为了计算最后的b，也就是矩阵O

所以 Self-attention 输入是 I,输出是 O,那你会发现说虽然是叫 attention,但是其实 Self-attention layer 裡面,唯一需要学的参数,就只有$W^q{W}^k{W}^v$而已,只有$W^q{W}^k{W}^v$是未知的,是需要透过我们的训练资料把它找出来的

Multi-head Self-attention

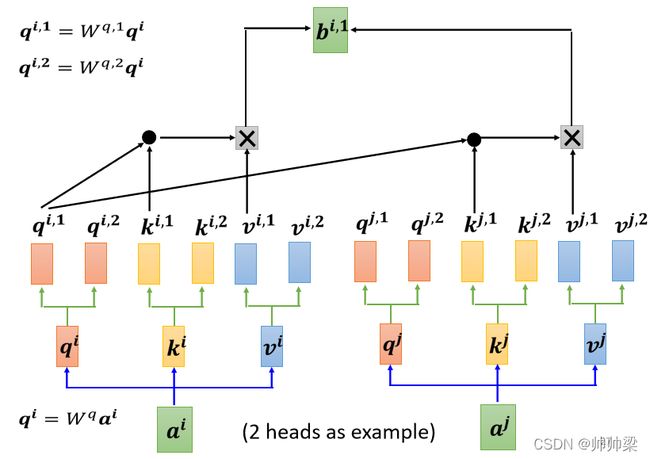
我们不能只有一个 q,我们应该要有多个 q,不同的 q 负责不同种类的相关性

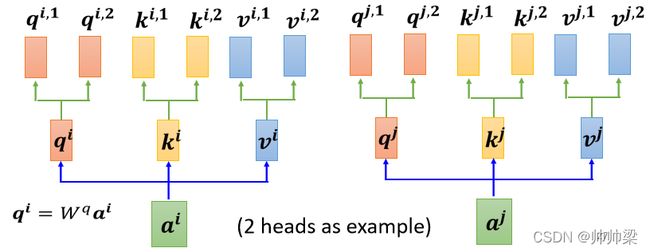
• 先把 a 乘上一个矩阵得到 q
• 再把 q 乘上另外两个矩阵,分别得到$q^1{q}^2$,那这边还有 这边是用两个上标,i 代表的是位置,然后这个 1 跟 2 代表是,这个位置的第几个 q,所以这边有$q^{i,1}{q}^{i,2}$,代表说我们有两个 head

我们认為这个问题,裡面有两种不同的相关性,是我们需要產生两种不同的 head,来找两种不同的相关性

对另外一个位置,也做一样的事情