相机标定python

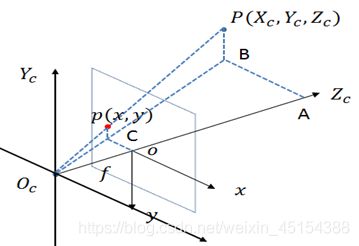
1、针孔照相机模型

针孔照相机模型（有时称为射影照相机模型）是计算机视觉中广泛使用的照相机模 型。对于大多数应用来说，针孔照相机模型简单，并且具有足够的精确度。这个名字来源于一种类似暗箱机的照相机，该照相机从一个小孔采集射到暗箱内部的光线。在光线投影到图像平面之前，从唯一一个点经过，也就是照相机中心$o_c$。

1.1 照相机矩阵

照相机矩阵可以分解为：$P=K[R|t]$
其中，R 是描述照相机方向的旋转矩阵，t 是描述照相机中心位置的三维平移向量，K为内标定矩阵，描述照相机的投影性质。标定矩阵仅和照相机自身的情况相关，通常情况下可以写成：
$$K=\left[\begin{array}{ccc}\alpha f& s& c_x\\ 0& f& c_y\\ 0& 0& 1\end{array}\right]$$
大多数情况下，可以将s设为0，纵横比例参数α设为1。f为图像平面和照相机中心间的距离(焦距)，标定矩阵K中剩余的唯一参数为光心（有时称主点）的坐标 $c=[c_x，c_y]$，光心的坐标常接近于图像宽度和高度的一半,因此唯一未知的变量是焦距 f。

1.2 三维点的投影

相机类的创建：

class Camera(object):
   """表示针孔照相机的类"""
   def __init__(self, P):
       """初始化 P = K[R|t] 照相机模型"""
       self.P = P
       self.K = None   # 标定矩阵
       self.R = None   # 旋转
       self.t = None   # 平移
       self.c = None   # 照相机中心
   def project(self, X):
       """X（4×n的数组）的投影点，并进行坐标归一化"""
       x = dot(self.P, X)
       for i in range(3):
           x[i] /= x[2]
       return x
   def rotation_matrix(a):
       """创建一个用于围绕向量a轴旋转的三维旋转矩阵"""
       R = eye(4)
       R[:3,:3] = linalg.expm([0,-a[2],a[1]],[a[2],0,-a[0]],[-a[1],a[0],0])
       return R

1.3 照相机矩阵的分解

如果给定方程（1.1节中）所示的照相机矩阵P，我们需要恢复内参数K以及照相机的位置t和姿势R。矩阵分块操作称为因子分解。这里，我们将使用一种矩阵因子分解的方法，称为RQ因子分解。将一个 3x3 矩阵 A 进行 RQ 分解是将其分解成为一个上三角阵 R 与一个正交阵（orthogonal matrix） Q 的乘积。要求矩阵 A 的秩为3，即满秩。

def factor(self):
    """将照相机矩阵分解为 K,R,t,其中, R=K[R|t]"""
    K,R = linalg.rq(self.P[:,:3])
    # 将K的对角线元素设为正值
    T = diag(sign(diag(K)))
    if linalg.det(T) < 0:
        T[1,1] *= -1
    self.K = dot(K,T)
    self.R = dot(T,R)   # T的逆矩阵为其自身
    self.t = dot(linalg.inv(self.K), self.P[:,3])        
    return self.K, self.R, self.t

1.4 照相机中心

照相机的中心C，是一个三维点，满足约束PC=0。故给定照相机投影矩阵P，我们可以计算出空间上照相机的所在位置。对于投影矩阵为$P=K[R|t]$的照相机，有$K[R|t]C=KRC+Kt=0$,故照相机的中心：$C=-R^{T}t$
计算照相机中心：

def center(self):
    if self.c is not None:
        return self.c
    else:
        #通过因子分解计算c
        self.factor()
        self.c = -dot(self.R.T,self.t)
        return self.c

2、照相机标定

在图像测量过程以及机器视觉应用中，为确定空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系，必须建立相机成像的几何模型，这些几何模型参数就是相机参数。在大多数条件下这些参数必须通过实验与计算才能得到，这个求解参数（内参、外参、畸变参数）的过程就称之为相机标定。特别的，在零失真相机标定法中，每一个像素矢量在空间都是独立标定的，无需知道相机内部的结构，无需建立几何模型。无论是在图像测量或者机器视觉应用中，相机参数的标定都是非常关键的环节，其标定结果的精度及算法的稳定性直接影响相机工作产生结果的准确性。因此，做好相机标定是做好后续工作的前提，提高标定精度是科研工作的重点所在。

标定步骤：

1. 打印一张棋盘格，把它贴在一个平面上，作为标定物。
2. 通过调整标定物或摄像机的方向，为标定物拍摄一些不同方向的照片。
3. 从照片中提取棋盘格角点。
4. 估算理想无畸变的情况下，五个内参和六个外参。
5. 应用最小二乘法估算实际存在径向畸变下的畸变系数。
6. 极大似然法，优化估计，提升估计精度

3、 代码：

# coding=utf-8
import cv2
import numpy as np
import glob

# 设置寻找亚像素角点的参数，采用的停止准则是最大循环次数30和最大误差容限0.001
criteria = (cv2.TERM_CRITERIA_MAX_ITER | cv2.TERM_CRITERIA_EPS, 30, 0.001)

# 获取标定板角点的位置
objp = np.zeros((11 * 8, 3), np.float32)
objp[:, :2] = np.mgrid[0:11, 0:8].T.reshape(-1, 2)  # 将世界坐标系建在标定板上，所有点的Z坐标全部为0，所以只需要赋值x和y

obj_points = []  # 存储3D点
img_points = []  # 存储2D点

images = glob.glob("D:\\pycharm\\machine learning\\1/tu/*.jpg")
i=0
for fname in images:
    img = cv2.imread(fname)
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    size = gray.shape[::-1]
    ret, corners = cv2.findChessboardCorners(gray, (11, 8), None)
    #print(corners)

    if ret:

        obj_points.append(objp)

        corners2 = cv2.cornerSubPix(gray, corners, (5, 5), (-1, -1), criteria)  # 在原角点的基础上寻找亚像素角点
        #print(corners2)
        if [corners2]:
            img_points.append(corners2)
        else:
            img_points.append(corners)

        cv2.drawChessboardCorners(img, (11, 8), corners, ret)  # 记住，OpenCV的绘制函数一般无返回值
        i+=1
        cv2.imwrite('qipan'+str(i)+'.jpg', img)
        cv2.waitKey(1500)

#print(len(img_points))
cv2.destroyAllWindows()

# 标定
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(obj_points, img_points, size, None, None)

print("ret:", ret)
print("mtx:", mtx) # 内参数矩阵
print("dist:", dist)  # 畸变系数   distortion cofficients = (k_1,k_2,p_1,p_2,k_3)
print("rvecs:", rvecs)  # 旋转向量  # 外参数
print("tvecs:", tvecs ) # 平移向量  # 外参数

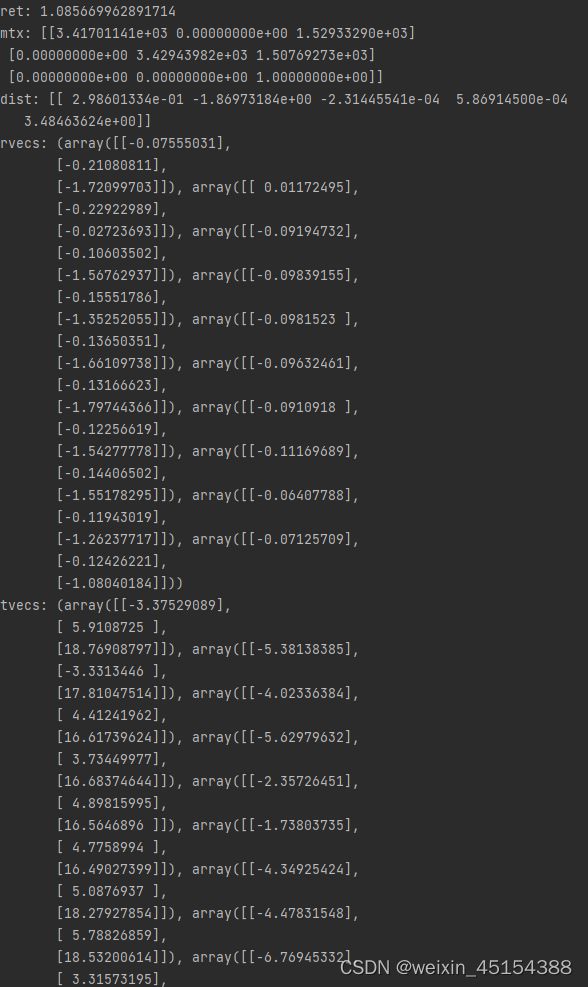
实验结果如下：
1、几乎全部为正面图时：
提取角点结果如下：

各参数结果：

因为在拍摄正面图时进行了旋转，故旋转向量较大

2、正侧面结合：
提取角点结果：

各参数：

可以发现，和正面图相比，通过多角度图片计算出的相机参数中，相机内参变化不大，畸变系数均减小，旋转向量减小。平移向量变化不大
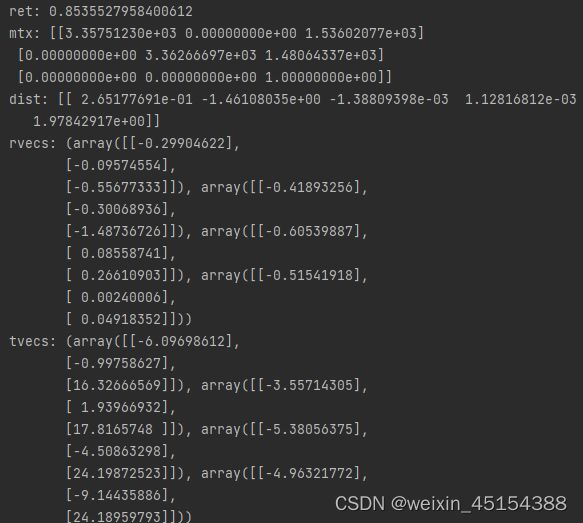
3、侧面多：
提取角点结果：

各参数：

和正面图相比，旋转向量略微下降，平移向量略微增加，切向畸变增加。