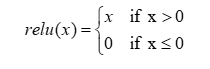20.神经网络中常见激活函数的总结

传统的激活函数选择的建议 

1. 优先Relu
2. 再考虑prelu、Leak Relu、Maxout
3. 再考虑tanh
4. 除非用作二分类的最后一层，其他一般不建议使用sigmoid

---

0.前言

在神经网络中，经常要使用到激活函数，对于激活函数的选用，参考指数族分布文章，根据神经网络的用途及其场景，加上对于激活函数的值域的了解，大致可以选定适合对应用途以及场景的激活函数。

对于分类器，最终输出的是输入样本在某一类上的可能性（概率），而概率值一般在[0,1]之间，因而最后一层输出的时候，可以选用值域在[0,1]之间的激活函数，比如sigmoid函数。

目录

传统的激活函数选择的建议 

0.前言

1.sigmoid函数

2.tanh激活函数

3.Relu激活函数

4.Leak Relu激活函数

5.Soft Plus激活函数

6.SoftMax函数

7.Maxout函数

8.Step函数

9.Identify函数

---

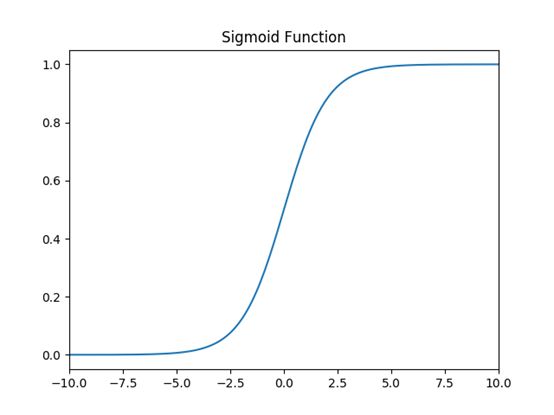
1.sigmoid函数

因其在 logistic 回归中的重要地位而被人熟知，值域在 0 到 1 之间。Logistic Sigmoid（或者按通常的叫法，Sigmoid）激活函数为神经网络引入了概率的概念。

函数的定义式：

值域：(0,1)

函数图像：

作图代码：

import numpy as np
import matplotlib.pyplot as plt
class Sigmiod():
    """
    def __init__(self):
        pass
    """
    def sigmiod(self):
        y = 1/(1+np.exp(-self))
        return y

    def plot_sigmoid(self,low,up,pace):
        x = np.arange(low,up,pace)
        y = Sigmiod.sigmiod(x)
        plt.plot(x,y)
        plt.show()

if __name__ == '__main__':
    Sigmiod().plot_sigmoid(-5,5,0.1)

缺点：

可能会发生梯度消失，小概率发生梯度爆炸。

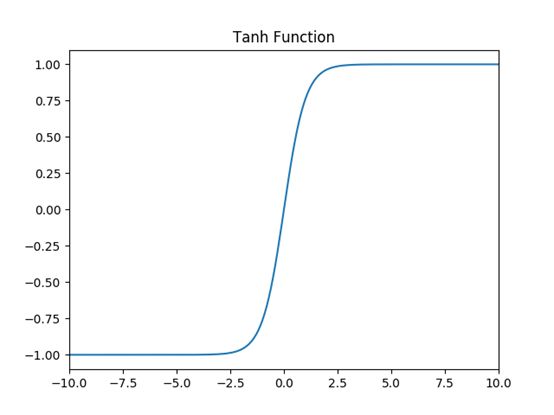
2.tanh激活函数

tanh具有很多神经网络所钟爱的特征。它是完全可微分的，反对称，对称中心在原点。为了解决学习缓慢和/或梯度消失问题，可以使用这个激活函数更加平缓的变体（log-log、softsign、symmetrical sigmoid 等等）

函数的定义式：

值域：(-1,1)

函数图像：

 作图代码：

import numpy as np
import matplotlib.pyplot as plt
class Sigmiod():
    """
    def __init__(self):
        pass
    """
    def sigmiod(self):
        y = (np.exp(self)-np.exp(-self))/(np.exp(self)+np.exp(-self))
        return y

    def plot_sigmoid(self,low,up,pace):
        x = np.arange(low,up,pace)
        y = Sigmiod.sigmiod(x)
        plt.plot(x,y)
        plt.show()

if __name__ == '__main__':
    Sigmiod().plot_sigmoid(-5,5,0.1)

特点： 

1.与sigmiod函数相似；
2.对比sigmiod函数：
（1）tanh激活函数均值为0，而sigmiod函数均为不为0，意味着自带了一个bias，相比tanh激活函数，sigmiod激活函数会让收敛变慢；
（2）tanh在原点的导数大于sigmiod在原点的导数，tanh相比于Sigmoid函数更容易训练，具有优越性。

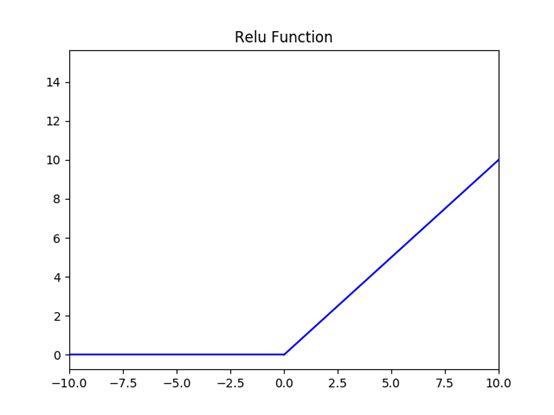
3.Relu激活函数

修正线性单元（Rectified Linear Unit，ReLU）是神经网络中最常用的激活函数。它保留了 step 函数的生物学启发（只有输入超出阈值时神经元才激活），不过当输入为正的时候，导数不为零，从而允许基于梯度的学习（尽管在 x=0 的时候，导数是未定义的）。使用这个函数能使计算变得很快，因为无论是函数还是其导数都不包含复杂的数学运算。然而，当输入为负值的时候，ReLU 的学习速度可能会变得很慢，甚至使神经元直接无效，因为此时输入小于零而梯度为零，从而其权重无法得到更新，在剩下的训练过程中会一直保持静默。

函数的定义式：

f(x) = max(0, x)

值域：[0,+∞)

函数图像：

作图代码：

import numpy as np
import matplotlib.pyplot as plt
class Sigmiod():
    """
    def __init__(self):
        pass
    """
    def sigmiod(self):
        y = np.array([])
        for i in range(len(self)):
            if self[i] > 0 :
                y= np.append(y,self[i])
            if self[i] <= 0:
                y = np.append(y,0)
        return y

    def plot_sigmoid(self,low,up,pace):
        x = np.arange(low,up,pace)
        y = Sigmiod.sigmiod(x)
        plt.plot(x,y)
        plt.show()

if __name__ == '__main__':
    Sigmiod().plot_sigmoid(-5,5,0.1)

特点：

1.单侧抑制，Relu实现稀疏后的模型能更高的挖掘相关特征；

2.对于线性函数，Relu的表达能力更强，尤其在深度学习中；

3.不存在梯度消失的问题，收敛速度也相对稳定。

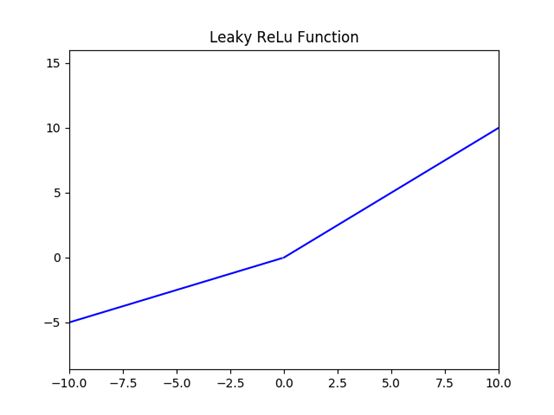
4.Leak Relu激活函数

函数的定义式：

值域：(-∞,+∞)

函数图像：（α为0.5的情况）

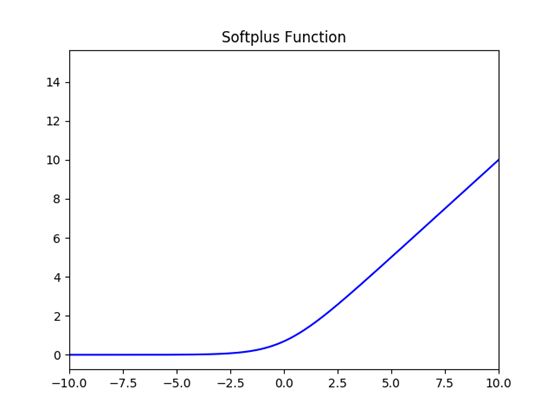
5.Soft Plus激活函数

函数的定义式：

值域：(0,+∞)

函数图像：

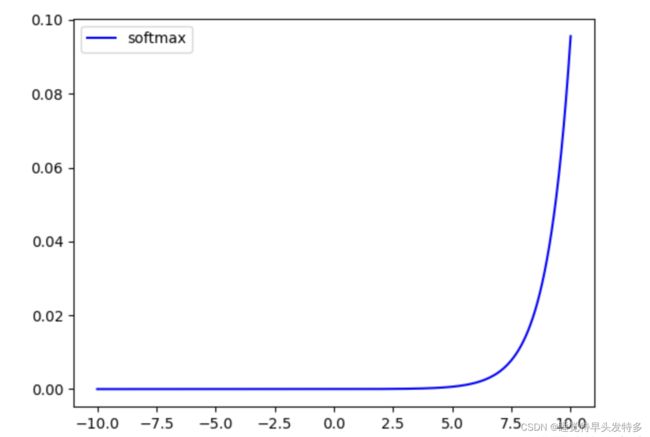
6.SoftMax函数

函数是用于多类分类问题的激活函数，在多类分类问题中，超过两个类标签则需要类成员关系。对于长度为K的任意实向量，Softmax函数可以将其压缩为长度为K，值在[0,1]范围内，并且向量中元素的总和为1的实向量。
函数的定义式：

​​​​​​​

定义域：R

值域：[0,1]

函数图像：

特点：

1.在零点不可微；

2.负输入的梯度为零，这意味着对于该区域的激活，权重不会在反向传播期间更新，因此会产生永不激活的死亡神经元。

7.Maxout函数

来源：Goodfellow I J, Warde-Farley D, Mirza M, et al. Maxout networks[J]. arXiv preprint arXiv:1302.4389, 2013.

论文链接：https://arxiv.org/pdf/1302.4389.pdf

Maxout函数来源于ICML上的一篇文献《Maxout Networks》，它可以理解为是神经网络中的一层网络，类似于池化层、卷积层一样。我们也可以把Maxout函数看成是网络的激活函数层，我们假设网络某一层的输入特征向量为：,也就是我们输入d个神经元。Maxout函数的输出如下（函数的定义式）：

值域：(-∞,+ ∞)

8.Step函数

激活函数 Step 更倾向于理论而不是实际，它模仿了生物神经元要么全有要么全无的属性。它无法应用于神经网络，因为其导数是 0（除了零点导数无定义以外），这意味着基于梯度的优化方法并不可行。

9.Identify函数

通过激活函数 Identity，节点的输入等于输出。它完美适合于潜在行为是线性（与线性回归相似）的任务。当存在非线性，单独使用该激活函数是不够的，但它依然可以在最终输出节点上作为激活函数用于回归任务。

深入学习：神经网络26 个激活函数汇总_TBYourHero的博客-CSDN博客_神经网络激活函数

神经网络中常见的几种激活函数_Tc.小浩的博客-CSDN博客_神经网络激活函数有哪些

激活函数(ReLU, Swish, Maxout)_mjiansun的博客-CSDN博客_maxout激活函数

常用激活函数activation function（Softmax、Sigmoid、Tanh、ReLU和Leaky ReLU) 附激活函数图像绘制python代码_卷不动的程序猿的博客-CSDN博客_softmax函数图像