支持向量机-线性不可分情况

上节回顾

线性可分情况下，支持向量机寻找最佳超平面的优化问题可以表示为：
$$\begin{array}{rl}最小化(Minimize):& \frac{1}{2}{\Vert \omega \Vert }^2\\ 限制条件:& y_i({\omega }^T{x}_i+b)\ge 1,(i=1\sim N)\end{array}$$

线性不可分情况

如果训练样本集是线性不可分的，那么以上优化问题的解，是什么呢？

在稍微思考下，以上的问题，是没有解的。

即：不存在 $\omega 和b$ 满足上面所有的 $N$ 个限制条件。

对于线性不可分的情况，我们要适当的放松限制条件。使上面的最优化问题变得有解。

放松限制条件的基本思路

$$\begin{array}{rl}放松限制& 条件的基本思路\\ & \Downarrow \\ 对每个训练样& 本及标签(X_i,Y_i)\\ & \Downarrow \\ 松弛& 变量{\delta }_i\\ (slack& variable)\end{array}$$

于是，我们可以将上面的 $N$ 个不等式的限制条件放松为如下的 $N$ 个不等式。
$$限制条件改写:y_i({\omega }^T{X}_i+b)\ge 1-{\delta }_i,(i=1\sim N)$$
只要松弛变量足够的大，上面的N个不等式的限制条件，是一定能够成立的。

当然，我们还要加入一些新的限制。阻止 ${\delta }_i$ 无限制的扩大，让他限制在一定的合理范围之内。。

最终的优化版本
$$\begin{array}{rl}最小化:& \frac{1}{2}\left||\omega \right|{|}^2+C\sum _{i=1}^N{\delta }_i或\frac{1}{2}\left||\omega \right|{|}^2+C\sum _{i=1}^N{\delta }_i^2\\ 限制条件:& \\ & (1){\delta }_i\ge 0,(i=1\sim N)\\ & (2)y_i(w^T{X}_i+b)\ge 1-{\delta }_i,(i=1\sim N)\end{array}$$
限制条件一，保证了每个δi是大于等于零的；限制条件二，使以前难以达到的不等式变得容易达到。
$$\begin{array}{rl}以前的目标函数只需要最小化& \frac{1}{2}\left||\omega \right|{|}^2\\ 现在的目标函数增加了一项& 所有{\delta }_i的和\end{array}$$
既要让 $\omega$ 越小越好，同时也要让 ${\delta }_i$ 越小越好。

其中，有一个比例因子 $C$ ，起到了平衡两项权重的作用。

在实际的应用当中，也可以取另一种目标函数，用 ${\delta }_i^2$ 代替 ${\delta }_i$ ，二者间的差距很小，可以看出，他们都是凸优化问题，都可以被高效的求解

其中比例因子 $C$ 是人为设定的，我们把人为设定的参数叫做算法的超参数（HYPER PARAMETER）。

在实验中，我们会不断变化 $C$ 的值，同时测试算法的识别率，选取效果最好的值作为超参数 $C$ 的取值。

可以看出，如果一个算法的超参数越多，那么手动调参的时间也就越多。这样，算法的自动性也会降低。

支持向量机是超参数很少的算法模型。

超参数很多的模型有人工神经网络，卷积神经网络等等。

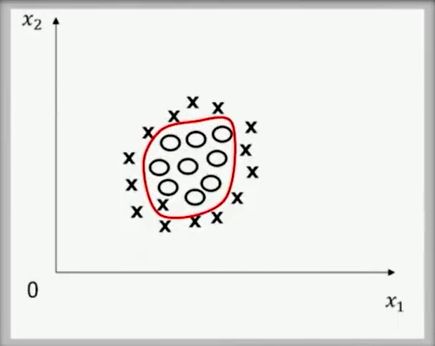
以下，是在线性不可分的情况下应用支持向量机的例子。

这里，$C$ 取了 10000，让 $\delta$ 的权重别的很大，使得它本身的值在优化过程中变得很小，接近于零，使得超平面和线性可分情况保持基本一致。
$$\begin{array}{rl}在线性不可分情& 况下应用支持向量机\\ & 取目标函数:\frac{1}{2}\left||\omega \right|{|}^2+C\sum _{i=1}^N{\delta }_i,C=10000\\ & 超平面和线性可分情况保持基本一致\end{array}$$

虽然支持向量机求出了一个超平面，但是这个解远远不能让人满意。分错了将近一半的训练样本，跟瞎猜没有区别。

那么问题出在哪里？

我们的算法模型是线性的，也就说我们假设分开两类的函数是直线或超平面，我们是在一簇直线或超平面中选择最适合分开两类样本的一条直线或超平面，但是线性模型的表现力是不够的，在这个例子中，很明显，能分开他们的是某种曲线，例如中间这个椭圆。

如果我们坚持分开两类的必须是直线，无论我们怎么选择，最终的结果都是不能使人满意的，因此，我们只能扩大可选的函数范围。

使他超越线性，才能使他应对各种复杂的线性不可分的情况。

思考

一个模型中的训练样本如下图所示，问能否对 $X_1,X_2$ 两个向量做某种非线性变换，把本来线性不可分的训练样本集变为线性可分？

低维到高维映射

如何扩大可选函数的范围，从而提高支持向量机处理非线性可分问题的能力？

支持向量机在这方面是独树一帜的，其他的算法比如人工神经网络、决策树等是直接产生更多可选函数。

例如在人工神经网络中，通过多层非线性函数的组合，能够产生类似于椭圆这样的曲线，从而分开这幅图中圆圈和叉。

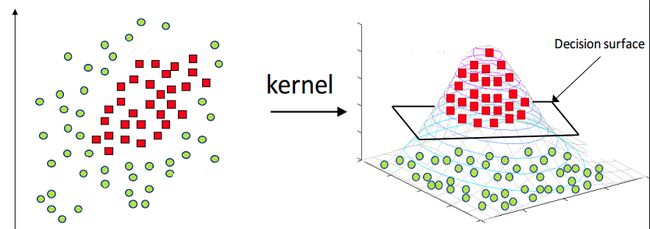
支持向量机却不是直接产生，而是通过将特征空间由低维映射到高维，然后在高维的特征空间中，仍然用线性的超平面对数据进行分类。下面给出两张直观的图片。

再给一个具体的例子，这是一个在低维线性不可分，而在高维中线性可分的例子。考察如下图所示的训练样本。

$$x_1=\left[\begin{array}{c}0\\ 0\end{array}\right]\in C_1{x}_2=\left[\begin{array}{c}1\\ 1\end{array}\right]\in C_1{x}_3=\left[\begin{array}{c}1\\ 0\end{array}\right]\in C_2{x}_4=\left[\begin{array}{c}0\\ 1\end{array}\right]\in C_2$$

构造一个二维到五维的映射 $\phi (x)$
$$\phi (x):x=\left[\begin{array}{c}a\\ b\end{array}\right]\to \phi (x)=\left[\begin{array}{c}{a}^2\\ b^2\\ a\\ b\\ ab\end{array}\right]$$
那么，可以得到如下经过变换的四个样本：
$$\phi (x_1)=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\end{array}\right]\phi (x_2)=\left[\begin{array}{c}1\\ 1\\ 1\\ 1\\ 1\end{array}\right]\phi (x_3)=\left[\begin{array}{c}1\\ 0\\ 1\\ 0\\ 0\end{array}\right]\phi (x_4)=\left[\begin{array}{c}0\\ 1\\ 0\\ 1\\ 0\end{array}\right]$$
经过此变换，原问题变得线性可分。
$$\begin{array}{rl}设：\omega =\left[\begin{array}{c}-1\\ -1\\ -1\\ -1\\ 6\end{array}\right]& b=1\\ {\omega }^T\phi (x_1)+b=1\ge 0& {\omega }^T\phi (x_2)+b=3\ge 0\\ {\omega }^T\phi (x_3)+b=-1<0& {\omega }^T\phi (x_4)+b=-1<0\\ & \\ 经由二维到& 五维的映射\phi (x)\\ 线性& 不可分\\ & \Downarrow \\ 线& 性可分\end{array}$$
我们这里不加证明的给出一个定理。
定理： 在 一 个 M 维 空 间 上 随 机 取 N 个 训 练 样 本 ， 随 机 的 对 每 个 训 练 样 本 赋 予 标 签 + 1 或 − 1 假 设 : 这 些 训 练 样 本 线 性 可 分 的 概 率 为 P ( M ) 当 M → ∞ 时 ， P ( M ) = 1 \begin{aligned} &\textbf{定理：} \newline \\ &&&在一个M维空间上随机取N个训练样本，随机的对每个训练样本赋予标签 +1 或 -1 \newline \\ &假设: \newline \\ &&&这些训练样本线性可分的概率为P(M) \newline \\ &&&当 \quad M \rightarrow \infty \quad 时，\quad P(M)=1 \end{aligned} ​定理：假设:​​在一个M维空间上随机取N个训练样本，随机的对每个训练样本赋予标签+1或−1这些训练样本线性可分的概率为P(M)当M→∞时，P(M)=1​
当特征空间的维度 $M$ 增加时，待估计参数 $(\omega ,b)$ 的维度也在跟随增加。

同时，整个算法模型的自由度也随之增加。

当然，这就更有可能分开低维空间无法分开的数据。
$$\begin{gathered} \begin{array}{rl}将训练样本& 由低维映射到高维 \\ \\ & \Downarrow \\ \\ 增大线性& 可分的概率\end{array} \end{gathered}$$
那么如何设计这个 $\phi (x)$ 就成为最关键的问题。

我们先放下对 $\phi (x)$ 的具体形式的探讨，先假设 $\phi (x)$ 已经确定。

来观察支持向量机优化问题将会做什么样的改变。
$$\begin{array}{rlrl}& 低维:& & \\ & 最小化:& & \frac{1}{2}\left||\omega \right|{|}^2+C\sum _{i=1}^N{\delta }_i或\frac{1}{2}\left||\omega \right|{|}^2+C\sum _{i=1}^N{\delta }_i^2\\ & 限制条件:& & \\ & & & (1){\delta }_i\ge 0,(i=1\sim N)\\ & & & (2)y_i(w^T{X}_i+b)\ge 1-{\delta }_i,(i=1\sim N)\\ & & & \\ & & \Downarrow x\to \phi (x)& \\ & & & \\ & 高维:& & \\ & 最小化:& & \frac{1}{2}\left||\omega \right|{|}^2+C\sum _{i=1}^N{\delta }_i或\frac{1}{2}\left||\omega \right|{|}^2+C\sum _{i=1}^N{\delta }_i^2\\ & 限制条件:& & \\ & & & (1){\delta }_i\ge 0,(i=1\sim N)\\ & & & (2)y_i[w^T\phi (X_i)+b]\ge 1-{\delta }_i,(i=1\sim N)\\ & & & \\ & & & X_i\Rightarrow 被\phi (X_i)替代\\ & & & \omega 维度与X_i维度相同\Rightarrow \omega 维度与\phi (X_i)维度相同\end{array}$$
高维情况下，优化问题的解法与低维情况下优化问题的解法是完全类似的，都可以利用凸优化问题进行求解。

思考

在支持向量机中，低维到高维的映射 $\phi (x)$ 具体取什么样的形式呢？

核函数的定义

引入了映射 $\phi (x)$ 后，就需要去研究它的具体形式，而支持向量机的提出者（$VladimirNaumovichVapnik$）关于 $\phi (x)$ 的形式是富有创意的。

我们不用知道 $\phi (x)$ 的具体形式，取而代之，如果对任意两个向量 $X_1,X_2$ 满足下列公式，那么我们仍然能够通过一些技巧来获得样本 $X$ 的类别信息，从而完成对测试样本类别的预测。
$$\begin{array}{rl}K(& X_1,X_2)=\phi (X_1{)}^T\phi (X_2)\\ & \Downarrow \\ 核& 函数(KernelFunction)\end{array}$$
核函数是一个实数，这一点也可以从等式的右边看出来，它是两个向量的内积。

举两个例子，来说明核函数预计低维到高维的映射 $\phi (x)$ 之间的相互关系。

1.已知映射 $\phi (x)$ ，求核函数 $K(X_1,X_2)$

​ 假设 $\phi (x)$ 是一个将二维向量映射为三维向量的映射。
$$\begin{gathered} \begin{array}{rl}X& =[x_1,x_2{]}^T \\ \\ \phi (X)=\phi ([x_1,x_2{]}^T)& =[x_1^2,x_1{x}_2,x_2^2{]}^T \\ \\ & \\ X_1=[x_{11},x_{12}{]}^T& X_2=[x_{21},x_{22}{]}^T \\ \\ & \\ \phi (X_1)& =[x_{11}^2,x_{11}{x}_{12},x_{12}^2{]}^T \\ \\ \phi (X_2)& =[x_{21}^2,x_{21}{x}_{22},x_{22}^2{]}^T \\ \\ & \\ K(X_1,X_2)& =\phi (X_1{)}^T\phi (X_2) \\ \\ & =[x_{11}^2,x_{11}{x}_{12},x_{12}^2][x_{21}^2,x_{21}{x}_{22},x_{22}^2{]}^T \\ \\ & =x_{11}^2{x}_{22}^2+x_{11}{x}_{12}{x}_{21}{x}_{22}+x_{12}^2{x}_{22}^2\end{array} \end{gathered}$$
2.已知核函数 $K(X_1,X_2)$ 求映射 $\phi (x)$

​ 假设 $X$ 是一个二维向量，且核函数 $K(X_1,X_2)$ 已知。
$$\begin{gathered} \begin{array}{rl}{X}_1=[x_{11},x_{12}{]}^T& X_2=[x_{21},x_{22}{]}^T \\ \\ & \\ K(X_1,X_2)& =(x_{11}{x}_{21}+x_{12}{x}_{22}+1{)}^2 \\ \\ & =x_{11}^2{x}_{21}^2+x_{12}^2{x}_{22}^2+1+2x_{11}{x}_{21}{x}_{12}{x}_{22}+2x_{11}{x}_{21}+2x_{12}{x}_{22} \\ \\ & =\phi (X_1{)}^T\phi (X_2) \\ \\ & \\ 假设:X& =[x_1,x_2{]}^T \\ \\ 则:\phi (X)& =\phi ([x_1,x_2{]}^T) \\ \\ & =[x_1^2,x_2^2,1,\sqrt{2}{x}_1{x}_2,\sqrt{2}{x}_1,\sqrt{2}{x}_2{]}^T \\ \\ & K(X_1,X_2)就是上面那个形式\end{array} \end{gathered}$$
核函数 $K(X_1,X_2)$ 和映射 $\phi (x)$ 是一一对应的关系，核函数的形式不能随意的取，需满足一定的条件——两个 $\phi$ 内积的形式。

Mercer’s Theorem

$$\begin{gathered} \begin{array}{rl}& K(X_1,X_2)能写成\phi (X_1{)}^T\phi (X_2)的充要条件 \\ \\ & ①K(X_1,X_2)=K(X_1,X_2)(交换性) \\ \\ & ②\forall C_i(i=1\sim N),\forall N有\sum _{i=1}^N\sum _{j=1}^N{C}_i{C}_{j}K(X_i,X_j)\ge 0(半正定性) \\ \\ & K满足交换性和半正定性\Rightarrow \phi 内积的形式\end{array} \end{gathered}$$

例如， 可以证明高斯核函数满足 $Merce{r}^{\prime }sTheorem$
$$K(X_1,X_2)=e^{-\frac{||X_1-X_2|{|}^2}{2{\sigma }^2}}$$
虽然我们无法知道 $\phi (x)$ 的具体形式，但是我们却可以通过一些方法，知道 ${\omega }^T\phi (x)+b$ 的值，进而我们可以知道测试样本 $X$ 的类别。

原问题与对偶问题

原问题（Prime problem）:

$$\begin{gathered} \begin{array}{rlr}& 最小化（Minimize）:& f(\omega ) \\ \\ & 限制条件（Subjectto）:& g_i(\omega )\le 0i=1\sim K \\ \\ & & h_i(\omega )=0i=1\sim m\end{array} \end{gathered}$$

$$\begin{gathered} 自变量为\omega \Leftarrow 多维向量 \\ 目标函数是f(\omega ) \end{gathered}$$

定义该原问题的对偶问题如下

$$\begin{gathered} \begin{array}{rl}定义函数:L(\omega ,\alpha ,\beta )& =f(\omega )+\sum _{i=1}^K{\alpha }_i{g}_i(\omega )+\sum _{i=1}^K{\beta }_i{h}_i(\omega ) \\ \\ & =f(\omega )+{\alpha }^{T}g(\omega )+{\beta }^{T}h(\omega ) \\ \\ & \\ 其中\alpha & =[{\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_K{]}^T \\ \\ \beta & =[{\beta }_1,{\beta }_2,\cdots ,{\beta }_M{]}^T \\ \\ g(\omega )& =[g_1(\omega ),g_2(\omega ),\cdots ,g_K(\omega ){]}^T \\ \\ h(\omega )& =[h_1(\omega ),h_2(\omega ),\cdots ,h_M(\omega ){]}^T \\ \end{array} \end{gathered}$$

在定义了 函数 $L(\omega ,\alpha ,\beta )$ 的基础上，对偶问题如下：

$$\begin{gathered} \begin{array}{rlr}最大化:& \theta (\alpha ,\beta )=\inf L(\omega ,\alpha ,\beta )，所有定义域内的\omega \\ & \\ 限制条件:& {\alpha }_i\ge 0,i=1\sim K \\ \inf :& 下确界 \\ \\ 整个公式& 清晰明了，即为取使得L最大化最小值的\theta ,\alpha ,\beta & \end{array} \end{gathered}$$

综合原问题和对偶问题的定义得到：

定理一：

如果 ${\omega }^{\ast }$ 是原问题的解，$({\alpha }^{\ast },{\beta }^{\ast })$ 是对偶问题的解则有：
$$f({\omega }^{\ast })\ge \theta ({\alpha }^{\ast },{\beta }^{\ast })$$
​ 证明：
$$\begin{gathered} \begin{array}{rl}\theta ({\alpha }^{\ast },{\beta }^{\ast })& =\inf L(\omega ,{\alpha }^{\ast },{\beta }^{\ast }) \\ \\ & \le L({\omega }^{\ast },{\alpha }^{\ast },{\beta }^{\ast }) \\ \\ & =f({\omega }^{\ast })+{\alpha }^{\ast T}g({\omega }^{\ast })+{\beta }^{\ast T}h({\omega }^{\ast }) \\ \\ & \le f({\omega }^{\ast }) \\ \\ 其中:g({\omega }^{\ast })& \le 0 \\ \\ h({\omega }^{\ast })& =0 \\ \\ \alpha ({\omega }^{\ast })& \ge 0 \\ \end{array} \end{gathered}$$
这个定理$(1)$告诉我们：原问题的解总是大于等于对偶问题的。

同时，定义对偶差距（Duality Gap）：
$$f({\omega }^{\ast })-\theta ({\alpha }^{\ast },{\beta }^{\ast })$$
显然，对偶差距是一个大于等于零的实数。

强对偶定理（Strong Duality Theorem）

$$如果g(\omega )=A\omega +b,h(\omega )=C\omega +b,f(\omega )为凸函数，则有f({\omega }^{\ast })=\theta ({\alpha }^{\ast },{\beta }^{\ast }),且对偶差距为0。$$

简单来说，如果：

​ 原问题的目标函数是凸函数，且限制条件是线性函数，则 $f({\omega }^{\ast })=\theta ({\alpha }^{\ast },{\beta }^{\ast })$ ，且对偶差距为 0。（证明参照：《Convex Optimization》）

KKT条件：

根据定理一推出的不等式：

​ 若 $f({\omega }^{\ast })=\theta ({\alpha }^{\ast },{\beta }^{\ast })$ ，则定理$(1)$中必然能够推出：对于所有的 $i=1\sim K$ 要么 ${\alpha }_i=0$ ，要么 $g_i({\omega }^{\ast })=0$ 。这个条件称为 KKT 条件。

转化为对偶问题

将支持向量机模型转化为对偶问题，首先要证明支持向量机的原问题满足强对偶问题。

回顾目前支持向量机的优化问题：
$$\begin{array}{rlrl}& 最小化:& & \frac{1}{2}\left||\omega \right|{|}^2+C\sum _{i=1}^N{\delta }_i或\frac{1}{2}\left||\omega \right|{|}^2+C\sum _{i=1}^N{\delta }_i^2\\ & 限制条件:& & \\ & & & (1){\delta }_i\ge 0,(i=1\sim N)\\ & & & (2)y_i[w^T\phi (X_i)+b]\ge 1-{\delta }_i,(i=1\sim N)\\ & & & \end{array}$$
原问题（Prime problem）:
$$\begin{gathered} \begin{array}{rlr}& 最小化（Minimize）:& f(\omega ) \\ \\ & 限制条件（Subjectto）:& g_i(\omega )\le 0i=1\sim K \\ \\ & & h_i(\omega )=0i=1\sim m \\ \end{array} \end{gathered}$$
原问题中，限制条件是小于等于0跟等于零，两种情况，所以我们要转换一下。
$$\begin{gathered} \begin{array}{rlrl}& 首先将 \\ & & \\ & & & {\delta }_i\ge 0(i=1\sim N)转换成{\delta }_i\le 0(i=1\sim N) \\ \\ & 得到 \\ & & \\ & 最小化:& & \frac{1}{2}\left||\omega \right|{|}^2-C\sum _{i=1}^N{\delta }_i \\ \\ & 限制条件: \\ & & \\ & & & (1){\delta }_i\le 0,(i=1\sim N)\\ & & & (2)y_i[w^T\phi (X_i)+b]\ge 1+{\delta }_i,(i=1\sim N)\\ & & & \end{array} \end{gathered}$$
在整理一下得：
$$\begin{gathered} \begin{array}{rlrlr}& 最小化:& & \frac{1}{2}\left||\omega \right|{|}^2-C\sum _{i=1}^N{\delta }_i或& \frac{1}{2}\left||\omega \right|{|}^2+C\sum _{i=1}^N{\delta }_i^2 \\ \\ & & & \Uparrow 情况一& \Uparrow 情况二 \\ \\ & 限制条件: \\ & & & \\ & & & (1){\delta }_i\le 0,& (i=1\sim N)\\ & & & (2)1+{\delta }_i-y_i{w}^T\phi (X_i)-y_{i}b\le 0,& (i=1\sim N)\\ & & & & \\ & & & 其中自变量{\omega }_{原}=({\omega }_{现},b,{\delta }_i)& \end{array} \end{gathered}$$
显然，限制条件是线性的，且目标函数是凸函数，满足强对偶定理。

其中，限制条件的一二两条属于 $g_i(\omega )$ ，不存在 $h_i(\omega )$ 。

根据以上信息写成对偶问题的形式：
$$\begin{gathered} \begin{array}{rlrlr}& 最大化:& & \theta (\alpha ,\beta )=\underset{\omega ,{\delta }_i,b}{\inf }\{\frac{1}{2}\left||\omega \right|{|}^2-C\sum _{i=1}^N{\delta }_i+\sum _{i=1}^N{\alpha }_i[1+{\delta }_i-y_i{\omega }^T\phi (X_i)-y_{i}b]+\sum _{i=1}^N{\beta }_i{\delta }_i\} \\ & \\ & 限制条件: \\ & & & (1){\alpha }_i\ge 0 \\ \\ & & & (2){\beta }_i\ge 0 \\ & \end{array} \end{gathered}$$
如何化为对偶问题：

对 $(\omega ,b,{\delta }_i)$ 求导并令导数为0。
$$\begin{gathered} \begin{array}{rlrlrlr}& (1)\frac{\partial \theta }{\partial \omega }=\omega -\sum _{i=1}^N{\alpha }_i{y}_i\phi (X_i)=0& \Rightarrow & & \omega =\sum _{i=1}^N{\alpha }_i{y}_i\phi (X_i)& & 向量的求导法则 \\ \\ & (2)\frac{\partial \theta }{\partial {\delta }_i}=-C+{\alpha }_i+{\beta }_i=0& \Rightarrow & & {\alpha }_i+{\beta }_i=C& & 常规的自变量求导 \\ \\ & (3)\frac{\partial \theta }{\partial b}=-\sum _{i=1}^N{\alpha }_i{y}_i=0& \Rightarrow & & \sum _{i=1}^N{\alpha }_i{y}_i=0& & 常规的自变量求导 \\ \end{array} \end{gathered}$$
将上述三个式子带入到等式中，得支持向量机的对偶问题：
$$\begin{gathered} \begin{array}{rlr}& 最大化:& \theta (\alpha ,\beta )=\sum _{i=1}^N{\alpha }_i-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{y}_i{y}_j{\alpha }_i{\alpha }_j\phi (X_i{)}^T\phi (X_j) \\ \\ & 限制条件: \\ & \\ & & (1)0\le {\alpha }_i\le C,(i=1\sim N) \\ \\ & & (2)\sum _{i=1}^N{\alpha }_i{y}_i=0,(i=1\sim N) \\ \\ & 其中:& \phi (X_i{)}^T\phi (X_j)就是核函数K(X_i,X_j)\end{array} \end{gathered}$$

算法流程

根据已知条件，解出所有的 ${\alpha }_i(i=1\sim N),\omega ={\sum }_{i=1}^N{\alpha }_i{y}_i\phi (X_i)$ 。由于 $\phi (x)$ 不知道是否具有显示表达，所以 $\omega$ 也不知道是否具有显示表达。但无需知道 $\omega$ 的显示表达。因为求 $\omega$ 的目的是得到 ${\omega }^T\phi (X_i)+b$ ，而该式子是为了得到 $y_i[{\omega }^T\phi (X_i)+b]$ 的值，从而判定样本的类比。而通过核函数 $K(X_i,X_j)$ ，能够越过求 $\omega$ 的这步，直接得到 ${\omega }^T\phi (X_i)+b$ 的值，从而判定样本的类别。那么剩下的问题就是如何求 $b$。

如何求 $b$

$$\begin{gathered} \begin{array}{rlrl}& 由于& \omega & =\sum _{j=1}^N{\alpha }_j{y}_j\phi (X_j) \\ \\ & 则& {\omega }^T\phi (X_i)& =\sum _{j=1}^N{\alpha }_j{y}_j\phi (X_j{)}^T\phi (X_i) \\ \\ & & & =\sum _{j=1}^N{\alpha }_j{y}_{j}K(X_j,X_i)\end{array} \end{gathered}$$

由 KKT 条件，可得：
$$\begin{gathered} \begin{array}{rl}& {\alpha }_i[1+{\delta }_i-y_i{\omega }^T\phi (X_i)-y_{i}b]=0 \\ \\ & {\beta }_i{\delta }_i=0\Rightarrow (C-{\alpha }_i){\delta }_i=0 \\ \end{array} \end{gathered}$$
如果对某个 $i$ ，${\alpha }_i\ne 0$ 且 ${\alpha }_i\ne C$ ，则根据 KKT 条件，必有 ${\delta }_i=0$ ;
$$\begin{gathered} \begin{array}{rl}& \because {\alpha }_i\ne 0,{\alpha }_i\ne C \\ \\ & \therefore C-{\alpha }_i\ne 0,1+{\delta }_i-y_i{\omega }^T\phi (X_i)-y_{i}b=0 \\ \\ 又& \because {\alpha }_i+{\beta }_i=C \\ \\ & \therefore 0<{\alpha }_i<C \\ \\ 又& \because y_i{\omega }^T\phi (X_i)=y_i\sum _{j=1}^N{\alpha }_j{y}_{j}K(X_j,X_i) \\ \\ & \therefore b=\frac{1-{\sum }_{j=1}^N{\alpha }_j{y}_i{y}_{j}K(X_j,X_i)}{y_i} \\ \end{array} \end{gathered}$$
随便取一个满足条件的 ${\alpha }_i$ ，便能求出 $b$。

判定测试样本类别

假定有一测试样本 $X$
$$\begin{gathered} \begin{array}{rl}& {\omega }^T\phi (X)+b \\ \\ \omega & =\sum _{j=1}^N{\alpha }_j{y}_j\phi (X_j) \\ \\ {\omega }^T\phi (X_i)+b& =\sum _{j=1}^N{\alpha }_j{y}_j\phi (X_j{)}^T\phi (X_i)+b \\ \\ & =\sum _{j=1}^N{\alpha }_j{y}_{j}K(X_j,X_i)+b\end{array} \end{gathered}$$

$$\begin{gathered} \begin{array}{r}如果\sum _{j=1}^N{\alpha }_j{y}_{j}K(X_j,X)+b\ge 0,那么X\in C_1 \\ \\ 如果\sum _{j=1}^N{\alpha }_j{y}_{j}K(X_j,X)+b<0,那么X\in C_2 \\ \end{array} \end{gathered}$$

训练流程

输入训练数据 $\{(X_i,y_i)\},i=1\sim N$ ，其中 $y_i=\pm 1$ 。

求 $\alpha$

$$\begin{gathered} \begin{array}{rlrl}& 最大化:& & \theta (\alpha )=\sum _{i=1}^N{\alpha }_i-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{y}_i{y}_j{\alpha }_i{\alpha }_j\phi (X_i{)}^T\phi (X_j) \\ \\ & 限制条件: \\ & & \\ & & & (1)0\le {\alpha }_i\le C,(i=1\sim N) \\ \\ & & & (2)\sum _{i=1}^N{\alpha }_i{y}_i=0,(i=1\sim N) \\ \\ & & & \\ & 其中:& & \phi (X_i{)}^T\phi (X_j)就是核函数K(X_i,X_j)\end{array} \end{gathered}$$

求 $b$

$$找一个{\alpha }_i\ne 0,{\alpha }_i\ne C则b=\frac{1-{\sum }_{j=1}^N{\alpha }_j{y}_i{y}_{j}K(X_j,X_i)}{y_i}$$

求出了 $\alpha$ 与 $b$ ，则完成了训练过程。

测试过程

考察测试数据 $X$ ，预测它的类别 $y$ 。
$$\begin{gathered} \begin{array}{r}如果\sum _{j=1}^N{\alpha }_j{y}_{j}K(X_j,X)+b\ge 0,那么y=+1 \\ \\ 如果\sum _{j=1}^N{\alpha }_j{y}_{j}K(X_j,X)+b<0,那么y=-1 \\ \end{array} \end{gathered}$$

思考

以上所有的讨论均基于最小化公式的前者，而后者同样也可以，其证明可自己推导。