基于数据挖掘的H公园客流量分析预测
第2章 H公园客流量初步分析
2.1 H公园客流量数据及初步时间序列分析方法选择
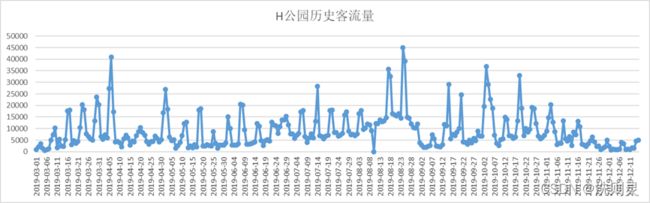
H公园开园于2018年11月,开园时间短,所拥有的历史数据只有一年多,缺少历年来数据的对比,相关人员本身无法根据这些数据得到有价值的信息,例如季节趋势等。并且客流量变化较大,无明显特征,除了天气、节假日等显著的影响之外,导致客流量变化大的影响因素还未被充分找到。H公园历史客流量如图2.1所示。
图2.1 H公园历史客流量
Fig. 2.1 Historical passenger flow of H Park
此外,利用数据挖掘技术对客流量进行准确的预测,其成果主要取决于以下几个方面:1)数据集的构造是否合理:在数据挖掘中,训练数据与测试数据必须要满足同分布的条件;2、特征集的特征是否充分且合理:理想的特征集中的特征,其特定的取值能够准确地指向某一信息,是多对一的关系,因此,如果特征集中缺少了重要的特征,或者特征过少,那么就可能导致同样的特征取值指向了不同的信息,从而导致错误的结果;3、算法的选择合理:算法不存在好坏之分,根据实际情况以及数据集的特点合理地选择算法,才能得到好的结果。
基于H公园的客流量存在的客观问题,以及为了利用数据挖掘得到好的结果所应该注意的问题,对H公园进行基本的时间序列分析是有必要的,有助于后续数据挖掘模型的构建。通过时间序列分析,可以找到基本的季节趋势,有助于解决数据集的选择问题,如果使用全部的历史数据,那么应该注意由于季节的原因,某些数据并非是同分布的,如果使用了较少的数据,又有训练数据过少的问题。并且,在时间序列分析中,除了分析基本趋势外,将天气、节假日、周末等基本信息输入之后,得到的结果有助于后续特征集构建,如果得到的结果拟合度不够好,说明在这些基本变量之外,还存在着重要变量。
基于以上分析,本文采用Facebook的时间序列预测模型fbprophet。从已有的应用看,fbprophet在处理存在季节趋势、节假日效应的时间序列数据时,有不错的效果。
2.2 H公园客流量时间序列分析
2.2.1 fbprophet原理
fbprophet是基于时间序列分解的分析方法改进而来的。一般而言,时间序列分解将时间序列 yt 分解成季节部分 St ,趋势部分 Tt ,剩余部分 Rt ,有如下公式:
yt=St+Tt+Rt (2.1)
在实际情况中,除了季节项,趋势项,剩余项之外,通常还有节假日的效应,因此在fbprophet中,Sean J.Taylor和Benjamin Letham同时考虑了以上四项:
yt=gt+st+ht+ϵt (2.2)
其中gt 为趋势项,它表示时间序列在非周期上面的变化趋势;st 表示周期项,或者称为季节项,一般来说是以周或者年为单位;ht 表示节假日项,表示在当天是否存在节假日;ϵt 表示误差项[16]。由于其中包含了节假日项,也是本文使用该框架的原因。
2.2.2 数据拟合
本文使用的数据直接来自于该公园的历史数据,因此,不存在缺失值、异常值等问题。由于H公园于2018年11月开园,因此其前期的历史客流量可能由于该原因人数较少,并且2018年12月至2019年2月存在较多的社会事件及特殊节日,因此使用的数据为2019年3月至2019年12月的数据。
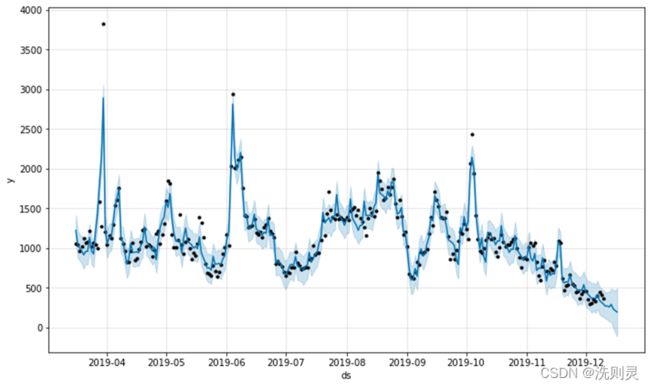
将数据输入fbprophet模型中后,通过调整参数,例如yearly_seasonality (在实例化模型时,可以为每个内置的季节性指定傅里叶级数)、changepoint_ prior_scale (默认情况下,该参数设置为0.05。增加它将使拟合趋势更加灵活) 等,得到一个较好的拟合结果,另外设置模型预测未来7天的数据。结果如图2.2所示。
2.2.3 拟合结果分析
通过对数据拟合的结果进行简单的观察可以发现,拟合结果较好但是从预测未来7天的结果来看,其未来7天的预测结果并不符合实际,并且延续了2019年10月至12月的下降趋势,说明该结果属于过拟合。而通过调整参数得到的其他结果,则存在拟合不足的问题,说明目前所拥有的数据信息,包括天气、周次、节假日,不能充足地反映实际情况,还存在很多未知且影响较大的因素,因此,后续模型的建立,需要考虑到能够帮助识别出这些潜在因素。
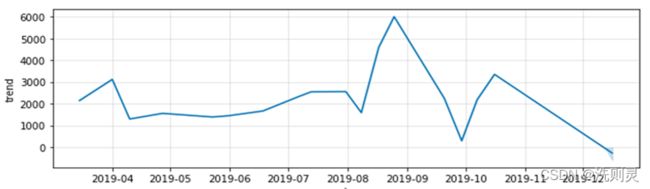
虽然该结果属于过拟合,但只代表了它不能用于预测,以上的数据拟合结果,还是反映出了季节趋势和周期性。季节趋势如图2.3所示。
图2.3 季节趋势
Fig. 2.3 Seasonal trend
从季节趋势图2.3可以明显看出,除了5、6月份以为,客流量在不同的月份波动较大,这涉及到了数据集构建的问题。数据集中,训练集和测试集的划分需要满足同分布的条件,如果有足够多且合理的特征集来表示数据,那么特征的不同取值,可以用来区别数据,因此,在合理且足够多的特征集的条件下,数据集可以比较大,不同分布的数据只需要不同的特征取值来表示即可。但在当前问题下,数据集则无法过大,因为时间距离过大的数据之间存在着较为明显的季节趋势,而在特征构造的问题上,季节是难以属于表示的特征,主要原因在于季节属于“模糊变量”,如果简单的以“0-1”来表示季节变化,则不符合实际的季节渐变趋势,而如果以百分位来表示,也无法找到合理的能够实际反映季节渐变趋势的数字。因此,为了找到更为合理的数据集长度,通过以上对于季节趋势的分析,本文决定使用一个月的数据长度作为训练集,测试集为未来一天。另外,通过以上分析,本文认为除了季节属于“模糊变量”以外,实际情况中还存在着其他未知的“模糊变量”。
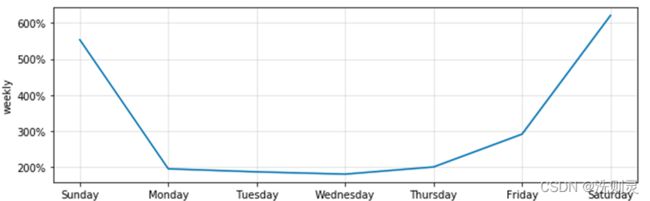
H公园客流量的周期性如图2.4所示。
从图2.4中可以较为明显的看出,其周期性较为符合人们的一般活动习惯,即工作日人数较少,周末人数较多,周五由于贴近周末,情况较为特殊。根据对于周期性的分析,除了一般结论之外,在后续的特征集构造问题上,应该注意周五的特殊问题,以使特征集能够更加准确地反映实际情况。
通过以上对于H公园历史客流量的基础分析,有助于本文后续模型的建立以及完善,帮助解决客观存在的问题与理想的数据挖掘应用之间存在的问题,从而使后续数据挖掘的应用更具合理性。
2.3 百度搜索指数分析
2.3.1 数据拟合与结果分析
本文直接从百度指数网站(http://index.baidu.com/v2/index.html#/)收集数据,百度搜索指数同样属于时间序列,并且与H公园客流量之间可能存在一定的相关性,如果能够对其加以利用,则对后续的客流量预测会有极大的帮助,因此,同样对其进行时间序列的基本分析是有必要的,同时还应探究其与H公园客流量之间的相关性。
由于搜索信息对于实际情况一般具有一定的“前兆效应”[9],经过合理地推断以及实验,本文决定将百度指数后移一天,之后输入fbpfophet算法中,其他输入不变,结果如图2.5所示。
图2.5 百度指数时间序列拟合结果
Fig. 2.5 Time series fitting result of Baidu index
从此百度指数的时间序列图看,与图2.2(数据拟合结果)的历史客流量对比,难以看出之间的相关性,因此需要判断其季节趋势和周期性。
通过对数据的季节性总结,得到以下季节趋势,如图2.6所示。
从季节趋势图上看,与图2.3(季节趋势)之间存在着波动幅度大小的差异,但百度指数的季节趋势仍然与H公园客流量的季节趋势有一定的相关性。
为进一步对比周期性,收索整理到百度指数的周期性如图2.7所示。
通过对比百度指数的周期性与H公园历史客流量的周期(图2.4)发现,其趋势大致相同。
通过以上的百度指数时间序列分析发现,百度指数可能与H公园客流量之间存在相关性,尽管并非特别明显。因此,为了更加准确的找到两者之间的相关性,还需做更进一步的检验。
2.3.2 相关性及协整检验
相关关系指变量之间存在着的非严格的不确定的关系,需要对它们进行深层次的分析,观察它们的密切程度。百度搜索指数与H公园历史客流量之间的相关性的计算采用了皮尔逊相关系数,其公式为:
r= (x-x')(y-y')(x-x')2(y-y')2 (2.3)
使用2019年3月至12月的全部数据进行相关性计算之后,得到两者之间的相关性为0.53448,相关性并不算太高。另外,由于上一节的讨论,本文采用的数据集为一个月的数据,因此,还需要考察两者之间一个月数据量的相关性。时间为2019年4月至12月,计算结果如图2.8所示。
由图2.8可以明显看出,百度指数与H公园历史客流量之间的相关性有较大的波动性,甚至存在负相关,且有些时间段相关性并不高。因此,百度指数可能并不是一个好的变量,因为该变量的性质随时有可能改变。
此外,百度搜索指数与H公园历史客流量有可能是属于非平稳的时间序列,因此,在两者之间建立回归模型可能会出现伪回归,因此,为了检验两者之间是否存在长期均衡关系,在此使用协整检验。
协整理论Engle和格兰杰Granger在1978年提出的,主要是为了解决时间序列的非平稳性,或许单个序列是非平稳的,但是通过协整可以建立起两个或者多个序列之间的平稳关系,进而充分应用平稳性的性质,考察多个序列之间的长期均衡关系,避免伪回归的问题。
进行协整检验有一个前提条件,即序列之间必须同阶单整。本文利用Eviews进行单位根检验,采用ADF检验百度指数和H公园客流量的平稳性[17]。H公园客流量的ADF检验结果如下表2.1。
表2.1 客流量ADF检验
Table 2.1 ADF test of Passenger flow
由结果可得,H公园客流量在10%的显著性水平下,是平稳的。
百度指数的ADF检验结果如下表2.2。
表2.2 百度指数ADF检验
Table 2.2 ADF test of Baidu index
而百度指数在10%的显著性水平下,是不平稳的。因此,在两个原序列并不满足进行协整检验的前提条件.将原序列经过一阶差分后再次进行ADF检验,发现在1%的显著性水平下,是平稳的,因此百度指数是属于一阶单整,但H公园客流量是零阶单整,因此,不能进行协整检验,可以认为百度指数与H公园客流量之间不存在长期均衡关系。
3.1 数据集构建
根据上一章对于H公园客流量的时间序列分析结果来看,H公园客流量在较长的一段时间内,其趋势变化是比较大的,但是由于目前对于H公园客流量的影响因素识别不够充分,仅仅只有天气情况、气温、周次以及节假日,以上几个影响因素显然不能够反映H公园客流量的趋势变化情况。因此,数据集不能以全部历史数据来建立,由于变量不能反映真实的客流量变化情况,使用全部历史数据要么导致拟合不足,要么导致过拟合,两种情况都不利于预测的准确性。
另外,除了季节是属于模糊变量之外,还有许多未知的影响因素同样属于模糊变量,难以被构造成数值的形式,因此这些变量将不可避免的以“噪声”的形式存在。而更长时间的历史数据之中,必然包含更多的“噪声”,并且这些“噪声”的影响是不可忽略的,并不属于随机变量“白噪声”,它们只是无法描述,有些“噪声”的影响大,有些“噪声”的影响小,并且方向也有可能不同。如果使用的历史数据过少,则难以训练模型。因此,如何选择数据集,使“噪声”更少且其影响更趋于一致,是关乎预测准确性的重要问题。
根据上一章中对于H公园历史客流量的季节趋势的分析,客流量月之间的波动是比较大的,说明超过一个月时间的历史数据,其包含的“噪声”可能较多。
综合以上考虑,本文选用30-50天的历史数据作为训练集,以未来一天作为测试集,即在预测阶段,完善后模型(包括调整完参数、特征集)需要以过去30-50天的数据进行训练,再以得到的模型预测未来一天的客流量。
以上的做法进行以下的考虑。H公园的客流量预测与典型的数据挖掘任务不同。H公园客流量预测任务属于短期预测,在其历史数据上,时间越接近的数据,其参考价值也越大,权重也越高,因此在建模时,必须对新鲜的数据给予更多的重视,它更多的包含对于未来一天的客流量有用的信息,并且其“噪声”的影响更可能趋于一致。例如,在最近一个月的时间中,客流量高于平均情况,虽然并不清楚是哪些“噪声”的影响,但是可以推测出未来一天的客流量情况也应该高于平均情况,因为这些“噪声”是模糊变量,不存在突然消失或者突然出现的情况,否则这些“噪声”便能够被以“0-1”的形式记录下来。另外,H公园的客流量预测与天气预报情况有一定的相似之处,天气预报对于未来越长时间的预测,准确率也越低。目前由于计算机技术的发展,数值预报方法更多地应用于天气预报上,主要是利用当前天气情况,和一些已知的物理定理,通过计算机求解出来[18]。在数据集使用的30-50天训练数据中,就包含了“当前的天气情况”——“噪声”,和较为符合30-50天情况的“物理定理”——通过训练得出的模型,因此,能够较为准确地预测未来一天的情况。
综上所述,考虑到预测H公园客流量存在的客观问题,与典型的使用全部历史数据并按一定比例划分为训练集和测试集不同,本文在不违反数据集使用原则的情况下,采用上述的数据集构建方式。
3.2 特征集构建
在数据挖掘中,通常认为数据决定了模型的上限,算法只能尽可能地逼近这个上限。这里数据指的是经过特征工程之后得到的数据。特征工程指的是把原始数据转变为模型的训练数据的过程,它的目的就是获取更好的训练数据特征,使得模型逼近这个上限。特征工程能使得模型的性能得到提升,构建得足够合理的特征集,有时甚至在简单的模型上也能取得不错的效果。特征工程在数据挖掘中占有非常重要的地位,一般认为特征工程包括特征构建、特征提取、特征选择三个部分。
特征构建指从原始数据中人工地找出一些有意义的特征,需要一定的经验。特征提取与特征选择都是为了从原始特征中找出最有效的特征。它们之间的区别是特征提取强调通过特征转换的方式得到一组具有明显物理或统计意义的特征;而特征选择是从特征集合中挑选一组具有明显物理或统计意义的特征子集。
在H公园客流量预测的特征集构建过程中,同样需要经过以上三个部分的流程。
(1)特征构建
由于H公园的开园时间短,历史数据少,并且处于发展中的L地区,相关人员对于其中重要的影响因素认识并不充分。因此,除了已知的对于客流量有较大影响的天气情况、气温、周次和节假日之外,并没有更多的原始特征。这显然是不充分的,即使实际情况中可能有许多模糊变量,但可记录的变量应该还有许多。因此在后续阶段,利用初步建立好的模型进行更多原始特征的识别,是非常有必要的。
(2)特征提取
特征提取强调了对于原始特征进行转换、组合等,以构建出更多可能包含重要信息的特征。原始特征为天气情况、气温、节假日和周次,对其所进行特征提取有以下几个方面。
1)天气情况
天气情况的取值不是数值型的,并且也不能以数值来代替,属于标称属性。因此,对它的处理采用了虚拟变量方法。虚拟变量又称虚设变量、名义变量或哑变量,用以反映质的属性的一个人工变量,是量化了的自变量,通常取值为“0”或“1”,有利于检验不同属性类型对因变量的作用,例如工资模型中的文化程度、季节对销售额的影响。
2)气温
原始气温特征记录了最高、最低气温,对其进行了取平均值的特征提取处理。
3)节假日。由于节假日出现频率大多只有一年一次,因此不使用虚拟变量方法进行处理,而是只记录“是否为节假日”。
4)周次
根据上一章的分析,H公园客流量存在着明显的周期性,引用图2.4(周期性),如下所示。该图反映了以下信息:周末的客流量较工作日多,且周六客流量大于周日;周五客流量较其他工作日多,而周三较少。根据以上信息,构造了“周三”、“周五”、“周六”、“周日”特征,为虚拟变量。以上的特征提取可能并不充分,可能还有更多信息隐藏在这些原始特征背后,后续实验将进一步对特征进行提取。
(3)特征选择
经过对于原始特征的提取之后,并不能够确定哪些特征是属于真正有意义的特征,因此需要对以上特征进行筛选。本文采用的筛选方式为计算特征的重要程度。需要在后续选择完算法之后的拟合与改进中进行。
以上内容即是对H公园客流量数据特征集的构建,结合实际情况与分析结果,初步选择了天气情况虚拟变量、“最高气温”、“最低气温”、“平均气温”、“是否为节假日”、“周末”、“周三”、“周五”、“周六”、“周日”。后续将对以上特征进行进一步的筛选,并根据测试结果进一步提取特征。
3.3 算法选择
算法的选择需要根据实际情况。根据上一章对于H公园客流量的分析,百度搜索指数与H公园客流量之间难以建立回归关系。而目前所构造的变量大多属于虚拟变量,取值范围为“0-1”,因此所构造的特征并不便于建立线性回归模型,线性回归模型公式为:
y=i=0nAixi+b (3.1)
xi 为特征的取值,Ai 为其系数,考虑如下一种情况:为了方便,假设某一数据仅有“周三”变量x3 取值为“1”,取余均为 “0”,假设其系数A3=500 ,常数项b=300 ,则预测客流量y=800 ,这中情况显然不符合实际情况,因为其他变量即使取值为0,对于预测客流量也是存在影响的。
经过以上考虑,以及为了使算法更加符合实际情况,本文决定采用集成树模型中的梯度提升树(GBDT)。
Boosting 指的是一种模型的组合方法,并且是递进式的,即根据上一次训练的结果进行改进。GBDT是基于Boosting的算法,是根据上一个决策树模型的结果的残差值,在优化残差的梯度方向上建立新的决策树模型。GBDT模型可以表示为:
Fx=m=1Mamhm(x) (3.2)
其中,am 为每棵树的权重,hm(x) 为第m棵树[19]。
以下为GBDT的简单例子,如图3.1所示。
据上图可以看出有些属性即使取值为“0”,也仍然存在影响,取值不同,影响也是非对称的,并且同一个特征在不同的树模型中有着不同的影响程度。另外,决策流程也符合人们考虑问题的习惯。
除了以上优点之外,该算法简单,不会有严重的过拟合现象,因此也适合特征少的数据。并且能够通过每一个特征在每一棵中的情况,计算其特征重要程度,方便于后续的特征选择。
3.4 拟合与参数调整
以上对于数据集、特征集和算法的选择并非最为恰当。根据所选择的数据集、特征集和算法对数据进行初步的拟合,有助判断选择是否合理,帮助进一步改进模型。到目前为止,模型的构建还存在以下问题:1、数据集的长度范围已经大致确定,当其具体长度有待验证;2、初步建立了特征集,不清楚是否有更加重要的特征还未提取,不清楚数据的预处理是否合理;3、确定了所使用的算法,算法的具体参数还未确定。为了解决以上更深入的细节问题,本文基于初步建立的模型进行了初步拟合。
为了避免初步拟合受到较多“噪声”的干扰,根据上一章中对于H公园客流量季节趋势的分析,选取了波动较小的4-5月份的数据,具体时间为2019年4月10日至2019年6月10日。
3.4.1 算法参数选择
数据决定了模型的上限,而算法则帮助模型逼近这个上限。因此,在不清楚模型的上限时,盲目处理数据作用不大,只有利用算法找到了当前模型的上限,才能够进一步进行数据集和特征集的处理。因此,改进选择从算法调参开始。
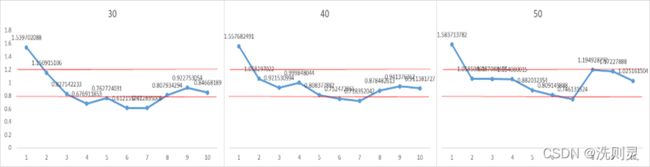
GBDT的参数最重要的有两个,一是“树分类器数量”,一是“树深”,即层数。为了选择最优参数,实验采用了枚举方法,两个参数之间两两组合,多次实验以找到最优参数。初步选取的参数为:“树深”:2,3,4;“树分类器数量”:20,30,40,共9个组合。数据集长度为40天的数据,预测2019年6月1日至6月10日的客流量。实验结果预测准确率——预测值/实际值,如图3.2所示。
其中,y轴刻度线表示1.2-0.8的准确率范围。
其拟合优度如表3.1所示。
表3.1 不同参数拟合优度
Table 3.1 The R square of different parameters
| 树深 |
数据集拟合优度 |
分类器20 |
分类器30 |
分类器40 |
| 2 |
测试集拟合优度 |
0.737698667 |
0.789662749 |
0.799813419 |
| 训练集拟合优度 |
0.833384224 |
0.882080981 |
0.909495921 |
|
| 3 |
测试集拟合优度 |
0.611726458 |
0.633048328 |
0.639252725 |
| 训练集拟合优度 |
0.933592443 |
0.973839722 |
0.986556954 |
|
| 4 |
测试集拟合优度 |
0.561688682 |
0.607578699 |
0.602194463 |
| 训练集拟合优度 |
0.96620375 |
0.989962383 |
0.996108805 |
数据挖掘中,模型在训练集上的拟合优度一般大于测试集,并且其差值不能太大,否则意味着过拟合,反之则为拟合不足。从拟合优度表3.1中,可以看出当“树深”超过2时,训练集和测试集的拟合优度差值显著大于0.1,达到了0.2-0.3的范围,属于明显的过拟合。并且,测试集上的拟合优度降低,也表示了准确率的降低。而在“树深”为2时,拟合优度差值为0.1左右,并且随着分类器数目加大,两者的拟合优度同步上升,并且始终在0.1左右。
根据以上准确率折线图3.2可以明显发现,在分类器数量一定的情况下,随着树深加大,准确率波动也更多,有更多的预测点离开了1.2-0.8的准确率范围;在树深一定的情况下,分类器数量的增加,波动则会减小。另外,根据折线图还可以明显看出,在“分类器-树深”为“40-2”时,波动小,并且准确率大部分在1.2-0.8之间,认为其准确率是比较高的。
另外,为了确认当分类器数量大于40时,其准确率是否还会提升,实验还测试了“分类器-树深”为“50-2”的情况。其准确率折线图如图3.3所示。
拟合优度如表3.2所示。
表3.2 参数“50-2”拟合优度
Table 3.2 The R square of parameter “50-2”
| 树深 |
数据集拟合优度 |
分类器50 |
| 2 |
测试集拟合优度 |
0.791259239 |
| 训练集拟合优度 |
0.926617952 |
从折线图3.3可以看出,相对于“分类器-树深”为“40-2”时,没有太多差别,说明已经接近模型上限。而从拟合优度表3.2中,可以看出,相对于“分类器-树深”为“40-2”,测试集拟合优度下降了,说明准确率下降,并且两者拟合优度之差,超过了1.2,说明开始出现了过拟合的现象。因此,“分类器-树深”为“50-2”并不优于“分类器-树深”为“40-2”。
综上所述,“分类器-树深”为“40-2”时,算法的表现已经接近上限,说明其为最优参数。
3.4.2 数据集长度选择
在以上算法参数的调优中,使用的数据集长度为40。在当前已经找出算法最优参数的情况下,进行数据集长度的调优,提升模型的上限。由于长度相差不大的数据集影响可能较为微小,且可能存在偶然性,因此,数据集长度测试为30、40、50的长度测试。准确率折线图如下图3.4所示。
图3.4 不同数据集长度预测准确率
Fig. 3.4 Prediction accuracy of different dataset size
拟合优度如表3.3所示。
表3.3 不同数据集长度拟合优度
Table 3.3 The R square of different dataset size
| 数据集拟合优度 |
长度30 |
长度40 |
长度50 |
| 测试集拟合优度 |
0.65106621 |
0.799813419 |
0.825105027 |
| 训练集拟合优度 |
0.970874438 |
0.909495921 |
0.857652401 |
从拟合优度表3.3可以看出,数据集长度为30时,测试集训练集拟合优度相差约0.32,明显存在过拟合。而长度为50时,虽然训练集拟合优度降低,但是测试集拟合优度上升,从准确率折线图3.4也可以看出,准确率更加接近于1,说明模型的泛化能力进一步增强,模型的上限提高了。
并且,在50的数据长度下,训练集和测试集拟合优度之差不到0.03,非常接近理想情况,进一步测试长度为60的数据集,意义不大,并且存在将更多不确定因素包含进来的风险,因此,确定长度为50的数据集为最优长度。
3.4.3 特征提取与选择
以上对于算法参数和数据集的拟合测试得到了较为不错的结果。但拟合结果较优不代表拟合过程足够切合实际,为了使模型更具稳健性,还应该对数据预处理结果和训练集拟合结果进行进一步的考察。以下进行训练集拟合结果的考察,拟合结果如图3.5所示。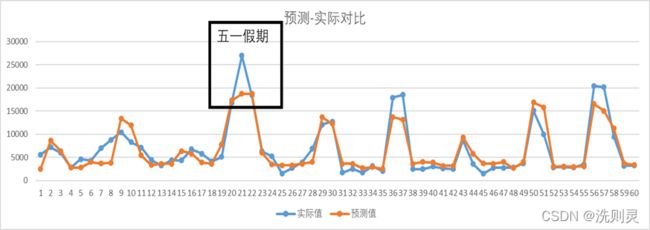
如图3.5,在该拟合结果中,较为值得关注的地方是“五一”假期,从预测结果来看,模型对于“五一”假期的人流量预测值是较为接近的,且超出其他非节假日假期的预测结果,但与实际情况并不相符。实际情况应该是越到节假日的中期,其客流量应该越大,而模型并没有将这点反映处理,只反映出了节假日假期相对与非节假日假期客流量的增多。因此,这一重要信息需要被反映出来,当前的测试集预测结果由于没有节假日假期,所以表现较好,这可能只是一种侥幸,模型目前没办法保证在遇到节假日假期时,能将这一重要信息反映出来。
另外,观察当前的特征集可以发现,天气情况虚拟变量、“最高气温”、“最低气温”、“平均气温”、“是否为节假日”、“周末”、“周三”、“周五”、“周六”、“周日”特征,并没有任何能够反映越到节假日的中期,客流量越大的信息,因此,需要进一步进行特征提取。
根据现有特征,本文进一步提取了“假期剩余天数”的特征,该特征能够较好地反映人们的生活习惯,即人们大多在假期前中部分出去游玩。 此外,还建立了“前一天是否为假期”、“后一天是否为假期”的特征,这两个特征能一定程度上反映人们的心理活动,并且有助于建立两条数据之间的联系。
下面进行数据预处理结果的考察。数据预处理之后,特征集为'最低气温', '最高气温', '平均气温', '周末', '节假日', '天气_中雨', '天气_多云', '天气_多云转中雨','天气_多云转晴', '天气_多云转阴', '天气_小雨', '天气_小雨转中雨', '天气_小雨转多云', '天气_小雨转晴', '天气_小雨转阴', '天气_晴', '天气_晴转多云', '天气_晴转小雨', '天气_阴转多云', '周次_星期三', '周次_星期五', '周次_星期六', '周次_星期日'。一共23个特征,其他特征没有变化,除了天气情况,而通过对于特征重要性的计算后发现,许多天气情况的特征重要性为0。特征重要性计算结果如下表3.4所示。
表3.4 特征重要性
Table 3.4 Feature importance
| 特征 |
特征重要性 |
特征 |
特征重要性 |
| 周末 |
0.518455061 |
天气_多云转晴 |
0 |
| 节假日 |
0.205005116 |
天气_多云转阴 |
0 |
| 最低气温 |
0.101491157 |
天气_小雨 |
0 |
| 最高气温 |
0.049115364 |
天气_小雨转晴 |
0 |
| 周次_星期日 |
0.046450439 |
天气_小雨转阴 |
0 |
| 平均气温 |
0.039506836 |
天气_晴 |
0 |
| 周次_星期六 |
0.026038064 |
天气_晴转多云 |
0 |
| 天气_小雨转中雨 |
0.006166683 |
天气_晴转小雨 |
0 |
| 天气_小雨转多云 |
0.006107776 |
天气_阴转多云 |
0 |
| 天气_中雨 |
0.001663504 |
周次_星期三 |
0 |
| 天气_多云 |
0 |
周次_星期五 |
0 |
| 天气_多云转中雨 |
0 |
从表3.4可以看出,天气的重要远远小于其他特征,这不符合实际情况。而结合天气特征多并且重要性低两个特点来考虑,说明天气特征可能冗余,需要进一步观察预处理结果。下表3.5为天气情况数据部分具体取值情况,截取自输出结果。
表3.5 天气情况取值
Table 3.5 The value of the weather feature
从表3.5可以看出,绝大部分天气情况取值为0,说明对于天气的预处理导致了特征稀疏的问题,即特征很多,而真正有效的特征很少。而天气情况并非无效特征,它反映了许多重要的信息,因此需要对天气特征的预处理做进一步的改善。
通过对于天气情况取值的观察后发现,天气的基本情况可以简单地分为六种,即晴、多云、阴、小雨、中雨、大雨,而天气情况的取值是基于天气基本情况进行组合,例如“小雨转中雨”,“多云转阴”等情况,并且还可能存在逆序的情况,例如“多云转阴”、“阴转多云”等,因此其取值情况可达30几种。而有些取值其影响是一样的,因此,采用虚拟变量的处理方法并不合理。因此,本文采用计分的形式重新处理天气特征。基本原则如下:将天气情况划分为六个基本特征,“晴、多云、阴、小雨、中雨、大雨”,其取值依据原天气特征涉及的基本特征进行计分,例如“多云转阴”,则计“多云-1”,“阴-1”,其余为0。这样的处理方法改善了特征稀疏的问题,并且同一个特征下,有更多的非“0”数据,有利于模型训练。下图3.6为重新进行了特征工程的拟合结果。
图3.6 改进后的模型拟合结果
Fig. 3.6 The fitting result of model after improving
可以看出,“五一”假期客流量的预测结果有了一定的改善,另外,模型的准确率折线图如下图3.7所示。
图3.7 改进后的预测准确率
Fig. 3.7 The prediction accuracy after improving
拟合优度如表3.6所示。
表3.6 改进后的拟合优度
Table 3.5 The R square after improving
| 数据集拟合优度 |
拟合优度 |
| 测试集拟合优度 |
0.81124343 |
| 训练集拟合优度 |
0.868465726 |
改进特征集之后的准确率除了较为异常的点以外,其余点的预测准确率仍然较高,而对比未改进特征集的模型和改进特征集之后的模型的拟合优度可以看出,拟合优度并没有太大变化,训练集和测试集拟合优度均在变化0.01左右,不具备太大的差异,可以接受该结果。
第4章 H公园客流量预测模型改进
4.1 影响因素识别
以上模型初步建立的过程是在平稳的季节趋势下进行的,并且模型在平稳的情况下,表现良好。但并不能由此说明模型在其他非4-5月份的情况下能有良好的表现,根据上一章的分析,数据中还存在着许多尚未识别的影响因素,根据H公园客流量的时间序列分析来看,大部分集中在非4-5月份的数据上。因此,为了使模型更加具有稳健性,还需要进行其他影响因素的识别。
影响因素的识别主要是根据模型的表现来进行的,例如,模型某段时间中表现稳定且高效,而到了下一段时间,其准确率突然出现较大的波动,则可以说明在这一段时间内,出现了对模型影响较大的影响因素。根据上一章对于“噪声”的讨论,影响因素又分为可识别和难以识别的,难以识别的影响因素主要是由于该影响因素具有模糊性,难以用数值进行表达,并且其对于数据的影响是缓慢的。对于这种难以识别的影响因素,根据上一章的讨论,本文已通过构造同分布的数据集来进行消除。而可识别的影响因素则不具备模糊性,其影响较为剧烈,往往表现为突然出现或者消失,会对模型的表现产生较大的影响,因此容易识别,并且可以以“0-1”虚拟变量来表示。以上是对影响因素识别可行性的探究,以下部分将根据影响因素的识别方法进行识别。
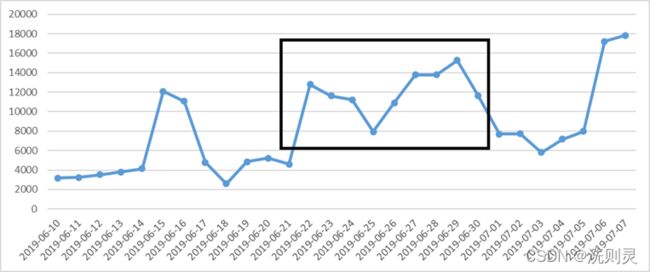
下图4.1是2019年6月10日至2019年7月7日的客流量折线图。
图4.1 6-7月客流量
从图中的一个月数据可以看出,6月22日至6月30日之间的数据明显存在异常,没有一般的周期性存在。
模型拟合情况如下图所示。
图4.2 6-7月拟合情况
Fig. 4.2 The fitting result from June to July
可以看出,模型对于6月15日至6月21日的拟合准确率较高,并且6月22日至6月30日的拟合仍然保持一定的周期性,但是由于出现了特殊情况,因此准确率下降。结合实际情况很容易知道,该异常主要是由于期末考试结束造成的,但具体的影响形式并不知道,因此需要进一步根据实际情况分析。通过对相关人员的访问,得知,中学期末考试结束于6月24日,小学期末考试结束于6月27日,并且该时间段存在之前未遇到的大雨的影响。
本文假设该段时间的人数异常,是由于中学生、小学生期末考试结束引起的,并根据历史数据取工作日客流量平均值为4000-5000,周末客流量为17000-18000。在以上的假设基础上做出以下的分析,消除中学生、小学生期末考试结束引起影响。
处理方式如表4.1所示。
表4.1 处理结果
Table 4.1 The Processing
上表根据对于中学生、小学生期末考试结束两个影响因素所造成的客流量变动的合理实际情况分析以及相关人员的分析,修正了这两个影响因素导致的客流量变动。可以看出,修正过后,数据较为符合一般情况和周期性。为了验证假设及修正是否合理,本文利用修正值进行模型的训练,重新预测2019年6月22日至30日的客流量。准确率折线图如下所示。
图4.3 修正后拟合结果图
Fig. 4.3 The fitting result after Processing
表4.2 修正后拟合优度
Table 4.2 The R square after Processing
| 数据集拟合优度 |
拟合优度 |
| 测试集拟合优度 |
0.931718003 |
| 训练集拟合优度 |
0.9486549 |
通过修正值的预测结果可以判断出,本文所作的假设是合理的,虽然在修正处理上较为理想化,但并非不符合实际情况的逻辑,因此可以认为2019年6月下旬的波动是由于中学生、小学生期末考试结束两个特殊影响因素共同造成的。因此,应将这两个特征记录下来。
通过以上特征识别过程,模型还识别了高中暑假、开学前一周、开学后一周、上海地区重大活动这几个特殊影响因素,过程不多做叙述。
以上内容是通过应用初步建立的模型对重要特征的进一步识别,以增强模型稳健性,特征识别不仅有助于模型的完善,其过程同样有助于相关人员对于H公园的客流量本质的理解,帮助H公园进行定制化建设。
4.2 减少噪声影响
以上的结果是建立在H公园只有一年的历史数据上,模型表现虽然存在波动,但总体表现不错,并且通过识别了更多的影响因素之后,模型表现更加稳健。但是,模型中仍然存在着不可控因素,即无法通过数值表达的模糊“噪声”的影响,根据H公园客流量的时间序列分析和预测结果,本文选择50天的历史数据以减少“噪声”影响,但“噪声”并不会就此被控制住,“噪声”的不可控表现在,它的影响程度可大可小,影响速度可快可慢,并且出现的时间不一定。因此,即使采用50天的历史数据,还是无法保证50天的数据服从同分布的条件,进而影响预测结果。
因此,使用H公园的历史同期数据就显得十分重要。历史同期数据中,毫无疑问存在相同的“噪声”的影响,存在着相同的季节影响因素和社会影响因素,并且影响程度大致相同。因此,采用历史同期数据可以使数据集更大程度上保持同分布的条件,同时使数据集扩大,更有利于模型的训练。因此结合历史50天的数据和历史同期数据,可以使模型不仅学习到当前的客流量规律,还能将历史的情况考虑进来,即“学习过去的经验,考虑当前的情况”,使模型更具稳健性,在遇到新的情况时不至于“惊慌失措”。
采用历史同期数据具体有以下三个方面的好处。
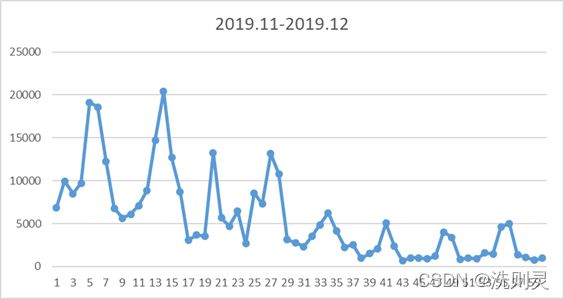
第一,考虑了季节信息。根据H公园客流量的时间序列分析,客流量存在着季节性,但其影响较为缓慢,无法利用虚拟变量或具体数值记录下来。并且“气温”的特征无法反映季节的影响,春季的18摄氏度与冬季18摄氏度影响肯定是不同的,因此在一些客流量受季节影响较大的时间段中,例如11月份至12月份,采用历史同期数据,可以使模型更多地考虑该季节的情况,而不仅仅是依据历史50天的情况。2019年11月份至12月份的客流量如下图4.4所示。
图4.4 11-12月客流量
Fig. 4.4 Passenger flow from November to December
从图4.4可以看出,受到季节的影响,客流量明显快速下降,因此,在预测12月份的客流量时,使用历史50天的数据,会大大降低准确性。而2018年12月份的历史同期数据如下图4.5所示。
从图4.4可以看出,受到季节的影响,客流量明显快速下降,因此,在预测12月份的客流量时,使用历史50天的数据,会大大降低准确性。而2018年12月份的历史同期数据如下图4.5所示。
图4.5 11-12月同期客流量
Fig. 4.5 Historic passenger flow from November to December
从图4.5可以发现,2018年12月与2019年12月的客流量是保持在同一范围的,因此采用2018年12月的历史同期数据,无疑使数据集更加满足同分布的条件。
第二,更精准地考虑了节假日的影响。由于节假日的名称不同,且为一年一度的数据,因此各个节假日分别建立特征,并不合理。于是本文采用将不同的节假日统一表示成“节假日”特征。此处理是基于实际情况的考虑,但仍然存在问题:1、某些节假日之间相隔时间长,当模型遇到节假日时,其50天的训练数据中可能没有节假日,例如,“元旦节”之前仅有“国庆节”,而且时间间隔超过50天,因此,模型不可能有好的准确率。2、不同节假日的影响可能不同,不同的节假日有不同的假期长度,其心理意义对于人们也是不一样的,“节假日”特征并没有做较好的区分。而以上两个问题通过采用历史同期数据是可以很方便地解决的。
第三, 解决上海地区重大活动与期末考试问题。上海地区重大活动与期末考试同样存在着与节假日相同的问题,其时间跨度大,并且影响程度不同,同样可以采用历史同期数据进行解决。
以上即是对于采用历史同期数据的益处的理论探究。下面将通过具体实例加以证明。
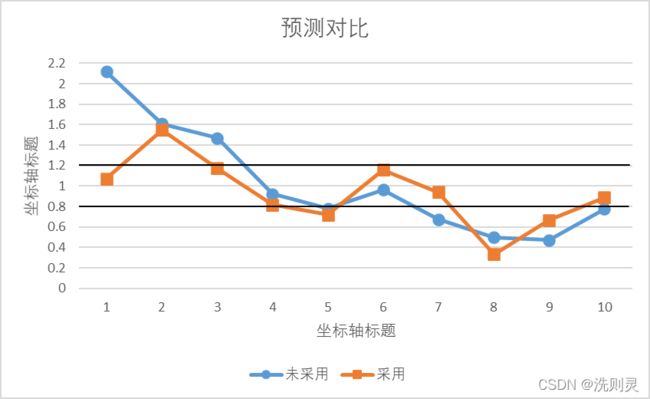
H公园开园于2018年11月,排除11月份开园效应的影响以及2019年1月份突发事件的影响,本文采用2018年12月份的历史同期数据与历史50天的数据预测2019年12月21-30日10天的客流量。未采用历史同期数据准确率与采用历史同期数据折线图对比。结果如图4.6所示。
图4.6 预测准确率对比
Fig. 4.6 Comparison of prediction accur
其MAPE(平均绝对百分比误差)如表4.3所示。
表4.3 MAPE对比
Table 4.3 Comparison of MAPE
| 实际值 |
原预测值 |
改进后预测值 |
| 2154 |
4561.819718 |
2307.534461 |
| 1664 |
2674.25004 |
2576.119024 |
| 1124 |
1654.378505 |
1320.046964 |
| 1638 |
1511.312055 |
1336.373949 |
| 1815 |
1418.732582 |
1308.440483 |
| 1591 |
1533.26083 |
1842.068579 |
| 1942 |
1309.204317 |
1829.045007 |
| 7281 |
3645.962598 |
2429.609045 |
| 4974 |
2359.296055 |
3326.163554 |
| 2331 |
1811.789517 |
2069.763515 |
| MAPE |
41.02% |
25.83% |
MAPE由41.02%下降到了25.83%,说明采用历史同期数据较大地改善了预测准确性。
在这里不使用拟合优度R平方系数的原因在于11-12月份的客流量较小,相较于其他月份的客流量,虽然模型预测的绝对误差相差不大,但是由于实际客流量变小的原因,相对误差增加了。从表4.2中的实际和预测值对比可以看出,某些日期的相对误差值达到了200%甚至300%以上,这在其他月份是不容易出现的。而在这里R平方系数非常容易受到这些“异常值”的影响,导致R平方系数大幅度下降,达到了0.2以下,对于反映模型预测值与实际值的偏离情况是非常不直观的,因此使用了平均绝对百分比误差,直接反映其偏离情况。
综上所述,用历史同期数据帮助构建数据集对于模型的表现有较大的帮助,在数据集方面,在增加了数据量的同时还更大程度上保证了数据的同分布原则;在特征工程方面,使得一些数据量较少的特征表现出了更多的信息;在算法方面,使得算法不仅能考虑历史情况,还能结合当前情况进行预测。因此,模型更加稳健,上限也提高了。
4.3 预测
通过以上的改进,模型已经基本完善,现通过预测检验模型的效果。
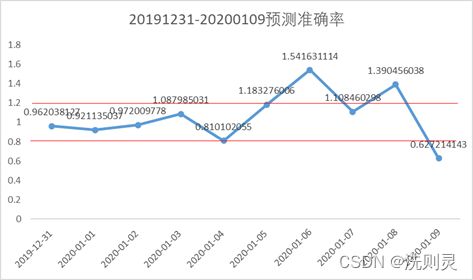
由于2020年1月份特殊事件的原因,所以测试集数据取2019年12月31日至2020年1月9日,共十天的数据。模型预测结果准确率如下图4.7所示。
图4.7 20191231-20200109预测
Fig. 4.7 The prediction from 2019.12.31 to 2020.01.09
其平均绝对百分比误差如下表4.4所示。
表4.4 20191231-20200109预测的MAPE
Table 4.4 The MAPE of the prediction from 2019.12.31 to 2020.01.09
| 日期 |
实际值 |
预测值 |
准确率 |
| 2019-12-31 |
10673 |
10267.83293 |
0.9620381 |
| 2020-01-01 |
3080 |
2837.095914 |
0.921135 |
| 2020-01-02 |
1555 |
1511.475205 |
0.9720098 |
| 2020-01-03 |
1326 |
1442.668151 |
1.087985 |
| 2020-01-04 |
3650 |
2956.872502 |
0.8101021 |
| 2020-01-05 |
3294 |
3897.711164 |
1.183276 |
| 2020-01-06 |
1380 |
2127.450937 |
1.5416311 |
| 2020-01-07 |
1252 |
1387.792293 |
1.1084603 |
| 2020-01-08 |
1087 |
1511.425714 |
1.390456 |
| 2020-01-09 |
1541 |
966.5369949 |
0.6272141 |
| MAPE |
20.19% |
从图3.7可以看出,预测准确率绝大部分在1.2-0.8之间,而对于误差较大的点,可以从表4.4看出,其绝对误差并不算太大。准确率误差大的原因在于其实际值较小,尽管如此,其MAPE为20.19%,说明模型还是取得了一个较好的结果。此外,观察元旦节前后的数据,发现元旦节前一天人流量是大于元旦节的,并且,2019年12月31日是星期二,为工作日,并没有放假,如果按照一般的思路预测,这一天的客流量并不会太多,但是模型还是给出了一个与实际情况相符的结果,并且准确率高,说明模型已经可以找到隐藏在表面数据背后的更深层的信息。
第5章 总结与展望
本文立足于数据挖掘应用的基本原则,致力于解决客观现实存在的问题与基本原则之间的差异。在不违反基本原则的前提下,不拘泥于典型的数据挖掘应用的表象,而深入其本质,从客观现实出发,建立了立足与基本原则又不脱离实际的数据挖掘模型,使数据挖掘的应用取得了较好的结果。
本项毕业设计深入分析H公园客流量存在的各种问题,首先,利用时间序列分析了H公园客流量的基本趋势,从中挖掘重要信息以及客观存在的问题,使得后续模型的建立能够不脱离实际。同时,还分析了搜索指数时间序列的特点,在回归检验以及数据挖掘原则的前提上,否定了将搜索指数作为变量进行后续实验的想法,立足实际,不盲目运用前人的经验。在了解了H公园客流量的重要信息以及客观存在的问题之后,立足于数据挖掘应用的基本原则,对模型的数据集、特征集和算法进行了初步设计。其中,数据集的使用不以典型的使用全部数据的数据挖掘模型为参考,立足于同分布的基本原则以及客观现实存在模糊变量导致不满足同分布条件的问题,初步设计了数据集;特征集的构建从实际出发,考虑了人们的生活习惯以及心理习惯,同时通过对数据预处理结果的考察,改进了预处理方式,使特征集的构造更加符合实际;算法的选择基于人们的决策习惯以及变量的影响特点。之后,通过初步拟合对以上三者进行了改进。最后,运用初步建立的模型进行了更多特征的识别,使模型更具稳健性。并且为了进一步消除模糊变量的影响,使数据集更加符合同分布的条件,加入了历史同期数据。最终,本文建立一个较为稳定且准确率较高的模型。
本文在模型的构建和算法上并没有太大的创新之处,但从“0”到“1”的模型建立过程仍然有一定参考价值即创新之处。在数据挖掘的基本原则和客观现实上,必然存在差异,导致某些基本假设和原则不成立,因此需要具体问题具体分析,经验只可借鉴不可照搬,对于所面临的问题仍然需要使用合适的工具进行分析,以发现客观问题的特点和基本原则上的差异,不同的客观现实必然有不同的问题,盲目使用而不考虑前提必然导致失败。在数据集的构建上,由于客观现实中存在难以表达的模糊变量的影响,为了使数据尽可能满足同分布条件,在数据集的选择上进行了一定的考虑,同时为了进一步使数据满足同分布的条件,加入了历史同期数据,与一般的使用全部数据不同,本文在为了满足同分布条件的目标上具有一定的创新。