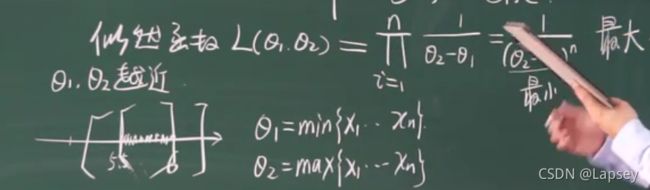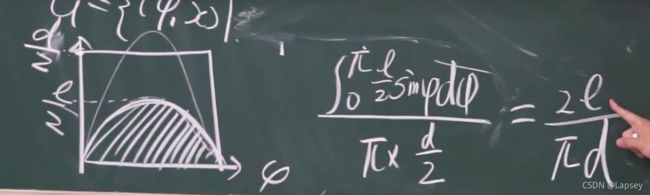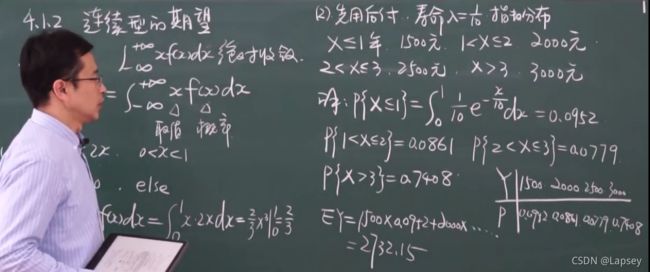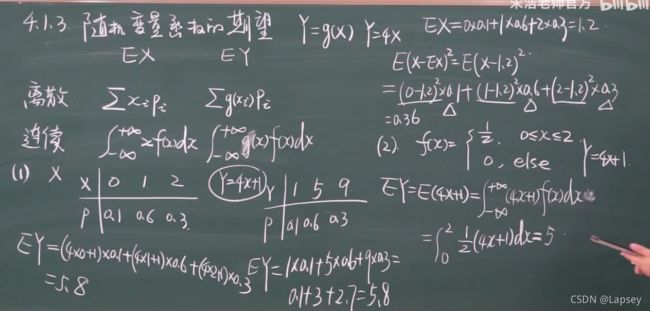宋浩《概率论与数理统计》自用笔记
文章目录
-
- 第一章 概率论的基本概念
-
-
- 古典概型
- 几何概型
- 公理化
- 条件概率
- 独立性
-
- 第二章 随机变量及其分布
-
-
- 离散型随机变量及其概率分布
- 连续型随机变量及其概率密度函数
- 分布函数
-
- 离散型的分布函数
- 连续型的分布函数
- 离散型分布
-
- 0-1分布
- 几何分布
- 二项分布
- 泊松分布
- 超几何分布
- 连续型分布
-
- 均匀分布
- 指数分布
- 正态分布
- 随机变量函数的分布
-
- 离散型
- 连续型
-
- 第三章 多维随机变量及其分布
-
- 二维离散型的联合分布和边缘分布
- 二维连续型的联合分布和边缘分布
- 第四章 随机变量的数字特征
-
- 离散型期望
- 连续型期望
- 随机变量函数
- 期望的性质
- 方差
- 方差的性质
- 原点矩和中心矩
- 第四章 大数定律及中心极限定理
-
- 大数定律
-
- 切比雪夫不等式
- 伯努利大数定律
- 切比雪夫大数定律
- 辛钦大数定律
- 独立同分布中心极限定理
-
- 德莫弗-拉普拉斯中心极限定理
- 第六章 样本和抽样分布
-
- 抽样分布
-
- 卡方分布
- t分布
- F分布
- 正态总体下的抽样分布
- 第七章 参数估计
-
- 矩估计定理
- 极大似然估计
- 无偏性
- 有效性
第一章 概率论的基本概念
- 差事件：A-B = A - AB = A(~B)，减去交集
- 互不相容事件：适用于多个事件
- 对立事件：并集为全集，只适用于两个事件
完备事件组：A1、…、An两两互不相容，并集为全集
德摩根定律：长线变短线，符号变
古典概型
- 有限个样本点
- 等可能性
几何概型
难题：朝指定的两条平行线投针，针与平行线相交的概率
- 相交要距离——垂直距离和角度肯定需要标记，而用中点表示垂直距离就可以用到已知量d
- 发现相交的不等式表示，得到x、d应满足的表达式
- 写出范围，用面积算概率
推广：可用来求π
结合定积分、绝对值等需注意
公理化
做题：画图、性4.5
如果概率=0，一定是不可能事件吗？不是！
扔到0.1这个点->概率为0也有可能发生
条件概率
做题：定义、乘法公式、相互独立…
清楚地定义事件很重要！
全概率公式：知道原因推结果
做题：列出所有情况（分类讨论）有时不止分一次情况
贝叶斯公式：知道结果推原因
做题：结合乘法公式和全概率公式使用
独立性
伯努利模型
第二章 随机变量及其分布
将事件用数学语言描述。
离散型：有限个+可列无穷
非离散型：主要看连续性
连续性：1个或多个区间
离散型随机变量及其概率分布
解题：
1、取值有哪些情况，概率求出来 列表
2、根据要求的范围来求
连续型随机变量及其概率密度函数
连续：端点无所谓，不影响概率
概率为0不一定不发生（多一个孤立点），概率为1不一定必然发生（少一个孤立点）。
以后多用积分解题
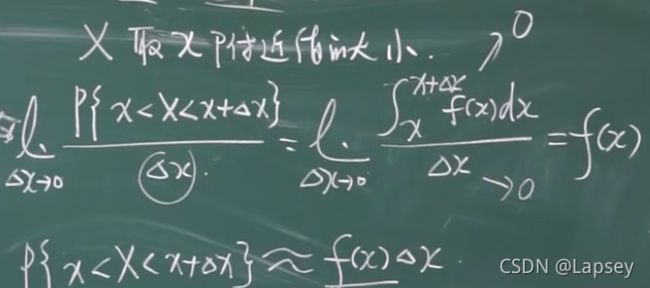
不计高阶无穷小时，分子就是柱状的面积。
分布函数
右连续：从右边逼近，极限值等于函数值
连续的三个条件：极限值存在、函数值存在、极限值等于函数值
a-0是从负无穷趋近a，取不到a。0相当于△0，一个0的无穷小，可以减小一点点。
离散型的分布函数
快捷方法：把X从小到大排列 然后画火柴棒
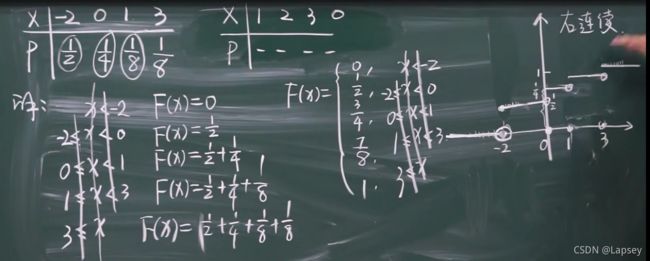
如果只知道每段的，每个点的概率就是向上跳跃的范围
连续型的分布函数
连续型端点上有没有无所谓，不像离散型会重点区分和计算！
注意连续型分布中，极限值等于端点值。
离散型分布
0-1分布
几何分布
看首次发生的词语。
二项分布
最可能值指n对应(n+1)p时，概率最大。类比p=0.5时n/2和(n+1)/2概率最大。
一人看一台，多了就不能及时维修。概率得（2）比（1）的效率反而高。难算：泊松
泊松分布
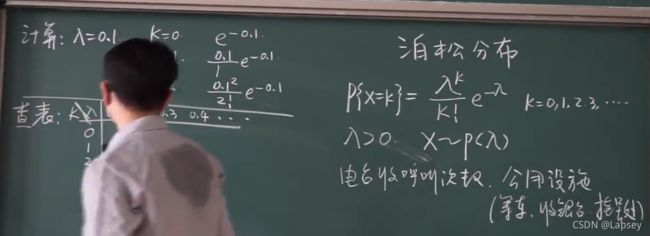
查表，看λ=6对应的值加起来什么时候超过0.95
也不一定要写公式，直接查表。
超几何分布
不放回抽样试验：通常要近似两次，否则不好算
连续型分布
均匀分布
把X限制好就行，这里几何概型做也很好做。
指数分布
无记忆性：用分布函数的公式计算即可。
可用比例相等来理解。
正态分布
上面的图是错的，下面的图是对的，毕竟总面积相等。
一般的正态分布如何化成标准正态分布？标准直接能做，一般的还要经过一步变换。
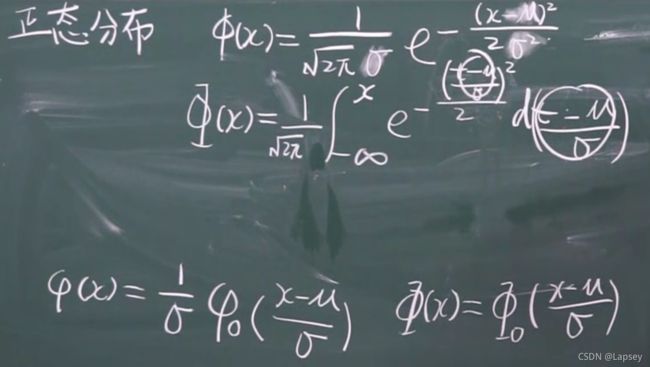
注意带不带0的区别：带0是标准分布
区别不大
3sigma准则，落在外头概率很小。
给定概率，求对应的点。
随机变量函数的分布
离散型
连续型
- 用X的分布函数表示Y的分布函数
- 两边求导得P概率密度函数 注意复合函数求导
均匀分布：
正态分布：
带平方或根号容易分类讨论，要细心：
注意分布函数和概率密度函数的区别~
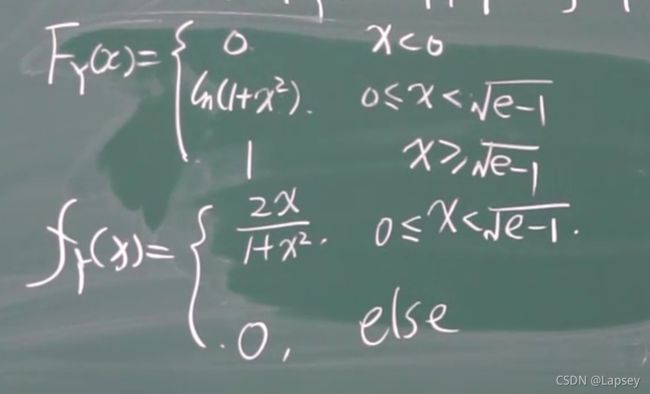
第三章 多维随机变量及其分布
一个样本空间的多个变量描述性质。
- 联合分布：概率为体积（三维空间中）。
- 边缘分布：
二维离散型的联合分布和边缘分布
- 联合分布：把xy两条直线画出来就简单了
- 边缘分布：对行和列求和即可。近似于只有一个变量了。
- 关系：用表格很好理解。
-
二维连续型的联合分布和边缘分布
（1）、（2）用公式求积分，（3）让x、y分别趋向正无穷
期中不考，待补充。
第四章 随机变量的数字特征
离散型期望
取值和概率相乘然后相加
连续型期望
X是连续型，Y是离散型，最终求Y。概率可与分布结合出题。
随机变量函数
直接代入算
多维也大同小异。
期望的性质
注意验证XY是否独立。
X拆解成Xi做。
方差
方差的性质
注意（5）右边是加号！！
原点矩和中心矩
高于4阶的矩极少使用。
第四章 大数定律及中心极限定理
大数定律
切比雪夫不等式
把EX和DX确认了代入即可。
伯努利大数定律
依概率收敛：虽然中间有不符合的，但大体是向极限逼近的。所以可以用频率逼近概率。
这里写的是同分布，所以不是切比雪夫大数定律的证明过程。
切比雪夫大数定律
若独立同分布：
辛钦大数定律
更强了，因为方差无要求。说明用平均数算期望靠谱。
独立同分布中心极限定理
做题：根据不同分布把EX和DX求出来。
德莫弗-拉普拉斯中心极限定理
当P（X=88）不好求时，巧妙地变成（87.5-88.5），因为概率误差很小。
二项分布难算怎么变成别的分布？泊松分布和正态分布均可，看n。
第六章 样本和抽样分布
样本之间都是独立的。
统计量不含未知参数！！！
注意样本方差进行了修正！
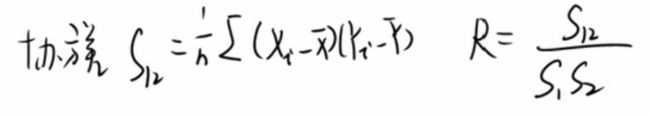
S12：两个随机变量的协方差 R：相关系数
加粗样式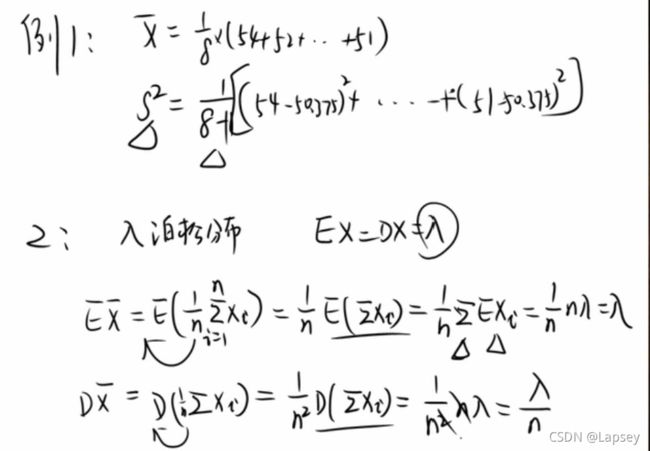
将样本取平均值后，方差会变小：波动性变小。
抽样分布
卡方分布
标准化：
t分布
结合正态分布和卡方分布！标准化！！
F分布
利用上分位数的定义：大于号。
正态总体下的抽样分布
各种分布去配。
第七章 参数估计
从样本的数据推断分布中的参数。
- 点估计：一个点 180
- 区间估计：一个区间 175-185 较简单 区间要小一点，落在区间的概率大一点
带尖号的为估计值。
矩估计定理
和分布类型无关。
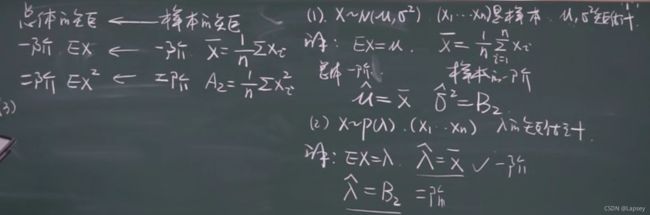
均匀分布的矩估计定理：做题时估计区间参数a、b
样本值为1、2、1.因为是估计，不是用概率和为1做题。
矩不一定都存在。
极大似然估计
按照左边的规律来！
为什么x<=0时没有乘上去，因为P=0说明样本中的事件没有发生，所以不包括在似然函数的范畴？
如果有两个参数：求偏导！！！把另一个变量看做常数。
均匀分布不能用求导的方法，事实上单调性可直接看出来，所以结果如下：
无偏性
有效性
方差越小越好 发现1/n有效？
无偏性求期望，有效性求方差。