背包问题一:01背包+完全背包+分组背包(附硬币问题汇总)
目录
一.01背包
1.状态转移方程
2.相关问题
3.相关优化
二.完全背包
1.状态转移方程
2.相关问题
3.相关优化
三.多重背包
1.状态转移方程
2.相关问题
3.相关优化
附:硬币问题
一.求最少硬币个数
二.所有硬币组合个数
一.01背包
1.状态转移方程
f[i][j]=max(f[i-1][j],f[i-1][j-k*w[i]]+k*v[i]//此时k=1
2.相关问题
①01-Knapscak 输出最优路径问题
注:必须采取二维状态记录,每i列只能选一次
#include
#include
#include
using namespace std;
const int N=105;
int w[N];
int v[N];
int path[N][1005];//path[i][j] 1
int dp[1005];
//dp[i][j]代表有i件商品可供选择有j这么大的容量可供盛放 这时可取得的最大商品价值
int main(){
int n,m;//商品件数和背包容量 ,要取得最大的价值
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>w[i];
}
for(int i=1;i<=n;i++){
cin>>v[i];
}
for(int i=1;i<=n;i++){
for(int j=m;j>=w[i];j--){
path[i][j]=0;
// dp[j]=max(dp[j-w[i]]+v[i],dp[j]);
if(dp[j-w[i]]+v[i]>dp[j]){
path[i][j]=1;
dp[j]=dp[j-w[i]]+v[i];
}
}
}
// cout< st;
int i=n;
int j=m;
while(i>0&&j>0){
if(path[i][j]==1){
st.push(i);
j-=w[i];
}
i--;
}
while(!st.empty()){
cout< 完全背包输出最优路径问题(选择了第i件后可以继续选)
#include
#include
#include
using namespace std;
const int N=105;
int w[N];
int v[N];
int path[N][1005];//path[i][j] 1
int dp[1005];
//dp[i][j]代表有i件商品可供选择有j这么大的容量可供盛放 这时可取得的最大商品价值
int main(){
int n,m;//商品件数和背包容量 ,要取得最大的价值
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>w[i];
}
for(int i=1;i<=n;i++){
cin>>v[i];
}
for(int i=1;i<=n;i++){
for(int j=w[i];j<=m;j++){
path[i][j]=0;
// dp[j]=max(dp[j-w[i]]+v[i],dp[j]);
if(dp[j-w[i]]+v[i]>dp[j]){
path[i][j]=1;
dp[j]=dp[j-w[i]]+v[i];
}
}
}
// cout< st;
int i=n;
int j=m;
while(i>0&&j>0){
if(path[i][j]==1){
st.push(i);
j-=w[i];//选择了i
}
else i--;//没选
}
while(!st.empty()){
cout< 扩展:1.输出01背包字典序最小方案
例:12. 背包问题求具体方案 - AcWing题库
//参考https://blog.csdn.net/yl_puyu/article/details/109960323
#include
#include
using namespace std;
const int N = 1005;
int n, m;
int v[N], w[N];
int f[N][N];
int main() {
cin >> n >> m;
for (int i = 1; i <= n; ++i) cin >> v[i] >> w[i];
for (int i = n; i >= 1; --i)
for (int j = 0; j <= m; ++j) {
f[i][j] = f[i + 1][j];
if (j >= v[i]) f[i][j] = max(f[i][j], f[i + 1][j - v[i]] + w[i]);
}
// 在此,f[1][m]就是最大数量
int j = m;
for (int i = 1; i <= n; ++i)
if (j >= v[i] && f[i][j] == f[i + 1][j - v[i]] + w[i]) {
cout << i << ' ';
j -= v[i];
}
return 0;
}
2.求背包所有最优方案的个数(恰好情况累加,非恰好注意状态转移即可)
例:11. 背包问题求方案数 - AcWing题库
#include
using namespace std;
const int N=10010,mod=1e9+7;
int f[N],g[N];
int V,v,w,n;
int main(){
cin>>n>>V;
for(int i=0;i<=V;i++)g[i]=1;
for(int i=1;i<=n;i++){
cin>>v>>w;
for(int j=V;j>=v;j--){
int left=f[j],right=f[j-v]+w;
f[j]=max(left,right);
if(left>right)g[j]=g[j];//不超过,没必要累加,搞清楚转移方向就可
else if(left 3.求背包所有最优方案的路径
②循环嵌套顺序
若当前容量循环是从后往前(多见于01滚动数组优化),此时嵌套顺序必须先物品,后容量。
例如:对于物品容量和价值分别为4,3,2,1和30,20,15背包容量为4。
如果先容量且倒序:那么我先确定当前容量为4,先放1,此时f(max)=f(4-1)+15,此时f(3)为0,相当于只算了放1,接着算放2,放3....显然放完时取最大放4的,价值为30;背包容量到3,就放个3的,价值为20;背包容量为2,就放个1的,价值为15.相当于每个容量我只放一个获得价值最大的
3.相关优化
一维滚动数组优化,直接覆盖,注意容量循环顺序倒序,才能保证取到i-1的物品
二.完全背包
1.状态转移方程
f[i][j]=max(f[i-1][j],f[i-1][j-k*w[i]]+k*v[i]//此时1<=k<=w/w[i]
由于完全背包问题求出最大值,所以需要枚举出所有情况时k=1/k=2/k=3....(k代表每i种物品取多少个作为一个整体)
此时可推导:f[i][j] = max(f[i-1][j-k*w[i]]+k*v[i])(0 <= k <= w/w[i])
下面开始变形:
把k=0拿出来单独考虑,即比较在【不放第i种物品】、【放第i种物品k件(k>=1)中结果最大的那个k】这两种情况下谁的结果更大
f[i][j] = max( f[i-1][j], max(f[i-1][j-k*w[i]]+k*v[i]) ) (k >= 1)
考虑上式【放第i种物品】这种情况:放的话至少得放1件,先把这确定的1件放进去,即:在第i件物品已经放入1件的状态下再考虑放入k(k>=0)件这种物品的结果是否更大。(如果k=1,说明第i种物品放了2件,因为前提状态是必然有一件物品已经放入)
f[i][j] = max( f[i-1][j], max( f[i-1][(j-w[i])-k*w[i]]+k*v[i] )+v[i] )(k >= 0)
结合之前蓝色的式子,可以发现,上式的后半部分就等于f[i][j - w[i]] + v[i],于是得出最终状态转移方程:f[i][j] = max(f[i-1][j], f[i][j-w[i]]+v[i])
2.相关问题
①嵌套顺序:由于完全背包是通过本层i件物品得来,所以容量遍历顺序必须从前往后,所以此时无论一维二维,嵌套顺序先后无所谓
②背包恰好装满问题
恰好装满初始化问题:无效状态赋值为负无穷,才能保证从有效状态转移
参考博客:01背包的变形问题----背包恰好装满_Iseno_V的博客-CSDN博客_背包问题变形
相关例题:HDU 1114
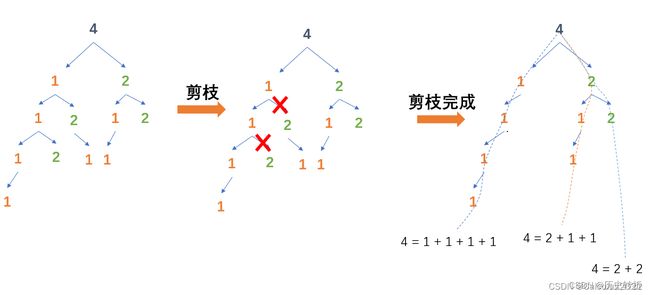
③嵌套顺序有关于排列/组合问题
参考博客: 【总结】用树形图和剪枝操作带你理解 完全背包问题中组合数和排列数问题
结合自己建立转移矩阵可以理解嵌套顺序带来的不同
相关例题:leetcode377. 组合总和 Ⅳ leetcode494. 目标和 leetcode70. 爬楼梯 leetcode139. 单词拆分
④完全背包最优路径问题(必用一维数组记录)
⑤打印完全背包所有最优路径
3.相关优化
依然采用滚动数组,注意遍历顺序从前往后
三.多重背包
1.状态转移方程
f[i][j]=max(f[i-1][j],f[i-1][j-k*w[i]]+k*v[i]//多重背包更多是一种解决思路,代表所有背包问题均可转换为01背包问题求解,纯多重背包的k范围为1<=k<=num[i]
2.相关问题
①纯多重背包问题的两种解决思路:
第一种意思是针对每种背包,先遍历容量,之后我每次只取1/2/3....num[i]种作为一个整体一个个放
#include
using namespace std;
const int N=1e5;//这时数组最大容量不能由商品种类数决定,而是总建树=种类*件数
int v[N];//价值
int w[N];//重量
int s[N];//每种商品的建树
int dp[N];
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>w[i]>>v[i]>>s[i];
}
for(int i=1;i<=n;i++){
for(int j=m;j>=w[i];j--){
for(int k=1;k<=s[i]&&k*w[i]<=j;k++){
dp[j]=max(dp[j],dp[j-k*w[i]]+k*v[i]);
}
}
}
// for(int i=1;i<=n;i++){
// for(int k=1;k<=s[i];k++){
// for(int j=m;j>=w[i];j--){
// if(k*w[i]<=j)dp[j]=max(dp[j],dp[j-k*w[i]]+k*v[i]);
// }
// }
// }
cout< 第二种意思是把每种背包当中每个全部铺开,再进行01背包判断
#include
using namespace std;
const int N=1e5;//这时数组最大容量不能由商品种类数决定,而是总建树=种类*件数
int v[N];//价值
int w[N];//重量
int dp[N];
int main(){
int n,m;
cin>>n>>m;
int vv,ww,c;
int cnt=1;//算作0-1背包的商品总建树
for(int i=1;i<=n;i++){
// cin>>w[i]>>v[i];
cin>>ww>>vv>>c;
for(int j=1;j<=c;j++){
v[cnt]=vv;
w[cnt]=ww;
cnt++;
}
}
for(int i=1;i<=cnt;i++){
for(int j=m;j>=w[i];j--){
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}
}
cout< ②变形多重背包:此时每种物品,k不能从1到num[i]一个个循环,此时采用①中第一个思路(抽取)将其转换为01背包问题求,例如hdu3092
#include
using namespace std;
#define maxn 3005
bool judge[maxn];
int ss[maxn],num;
int ans[maxn];
double dp[maxn];
void init()
{
memset(judge,true,sizeof(judge));
num=0;
judge[0]=judge[1]=false;
for(int i=2;i>s>>m){
memset(dp,0,sizeof(dp));
for(int i=0;i<=s;i++)ans[i]=1;
for(int i=0;ss[i]<=s;i++){
double tmp=log(ss[i]*1.0);
for(int j=s;j>=ss[i];j--){
for(int p=ss[i],k=1;p<=j;p*=ss[i],k++){//抽取k种,转换为01背包问题
if(dp[j-p]+tmp*k>dp[j]){
dp[j]=dp[j-p]+tmp*k;
ans[j]=ans[j-p]*p%m;
}
}
}
}
cout< 3.相关优化
①对于铺开的思路,由于对于任意一个数字来说,都可以用一个二进制来表达,如7 ,二进制为“111”,可以被划分为个数分别为1、2和4的三堆物品,但我们此时并不是完全采用二进制分.;以 9为例,先划分出一个1,再划分出 2,再划分出 4,最后剩下了一个 2,2小分为一堆.此时变为时间复杂度
的01背包问题
#include
#include
using namespace std;
const int N=1e5;
int v[N];//价值
int w[N];//重量
int dp[N];
struct node{
int w;
int v;
node(int w,int v):w(w),v(v){};
};
int main(){
int n,m;
cin>>n>>m;
int ww,vv,s;
vector good;
for(int i=1;i<=n;i++){
//一个一个拆成0-1背包 ,N`=N*s,N`*v会超时
// 有这么几个数,每个数选或不选,一定能用这几个数拼出x
cin>>ww>>vv>>s;
for(int k=1;k<=s;k*=2){//这s件不拆成1、1、1、1,而是1,2,4,
s-=k;
good.push_back(node(k*ww,k*vv));
}
if(s>0)good.push_back(node(s*ww,s*vv));
}
int len=good.size();
for(int i=0;i=good[i].w;j--){
dp[j]=max(dp[j],dp[j-good[i].w]+good[i].v);
}
}
cout< ②由于num[i]的大小不确定的,若num[i]*w[i]>W,此时num[i]>w/w[i],求得k<=w/w[i],此时,这一部分便等同于完全背包问题,可减少循环,例如hdu2844
#include
using namespace std;
const int maxn=1e5+10;
int a[maxn],c[maxn],dp[maxn];
int n,m;
int main(){
while(cin>>n>>m){
if(n==0||m==0)break;
int ans=0;
memset(dp,0,sizeof(dp));
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=n;i++){
cin>>c[i];
}
for(int i=1;i<=n;i++){
if(a[i]*c[i]>m){//转换为完全背包
for(int j=a[i];j<=m;j++){
dp[j]=max(dp[j],dp[j-a[i]]+a[i]);
}
}
else{
int sum=c[i];
for(int k=1;k<=sum;k<<=1){//二进制优化
for(int j=m;j>=k*a[i];j--){
dp[j]=max(dp[j],dp[j-k*a[i]]+a[i]*k);
}
sum-=k;
}
if(sum>0){
for(int j=m;j>=sum*a[i];j--){
dp[j]=max(dp[j],dp[j-sum*a[i]]+a[i]*sum);
}
}
}
}
for(int i=1;i<=m;i++){
if(dp[i]==i)ans++;
}
cout< ③单调队列优化
附:硬币问题
本质是背包问题,先确定背包类型决定框架
一.求最少硬币个数
例1:leetcode322. 零钱兑换
分析:无限个数,为完全背包问题。易得f[j]=min(f[j],f[j-num[i]]+1)
扩展:1.打印最少硬币组合 2.打印所有最少硬币组合
例2:设有n 种不同面值的硬币,各硬币的面值存于数组T[1:n ]中。现要用这些面值的硬币来找钱。可以使用的各种面值的硬币个数存于数组Coins[1:n ]中。对任意钱数0≤m≤20001,设计一个用最少硬币找钱m 的方法。
分析:有限个数,为多重背包问题,处理方法依旧
#include
#define MAX 20002
#define INF 9999999
using namespace std;
int n,m;
int a[100],b[100];
int main()
{
cin>>n;
int sum=0;
int c[MAX];//数组 c[]存放要找的最少硬币个数
for(int i=0;i>a[i]>>b[i];
sum+=a[i]*b[i];
}
cin>>m;
//问题无解
if(sum= a[i]; --k)
c[k] = min(c[k], c[k - a[i]] + 1);
}
}
cout< //还可以用二进制进行优化,这里不展开了,同多重背包问题
二.所有硬币组合
论证过程:AcWing 900. 整数划分 (求方案数、朴素做法 、等价变形 ) - AcWing
f[i][j]f[i][j] 表示前i个整数(1,2…,i)恰好拼成j的方案数
求方案数:把集合选0个i,1个i,2个i,…全部加起来
f[i][j] = f[i - 1][j] + f[i - 1][j - i] + f[i - 1][j - 2 * i] + ...;
f[i][j - i] = f[i - 1][j - i] + f[i - 1][j - 2 * i] + ...;
因此 f[i][j]=f[i−1][j]+f[i][j−i];f[i][j]=f[i−1][j]+f[i][j−i]; (这一步类似完全背包的推导)
f[i][j] = f[i - 1][j] + f[i][j - i]
①求个数
例一:leetcode518. 零钱兑换 II
分析:数量不限,方案累加(恰好问题),求组合个数,可得f[i]+=f[i-num[i]],注意嵌套顺序
例二:hdu2069-Coin Change
分析:多了总数量的限制,建立总数量的转移矩阵,可得f[j][k]+=f[j-num[i]][k-1]
②求所有路径
例:打印零钱兑换|| 的所有方案组合(求完全背包所有路径变式)
#include
using namespace std;
class Solution {
public:
vector> change(int amount, vector& coins)
{
vector dp(amount + 1, 0);
vector>> combiation(amount + 1);//记录所有具体的组合
dp[0] = 1;
for (int i = 0; i < coins.size(); i++) // 遍历物品
{
for(int j=coins[i];j<=amount;j++)// 遍历背包
{
if(j==coins[i])
{
dp[j] += 1;
combiation[j].push_back(multiset{j});
}
if(j>coins[i])
{
dp[j] += dp[j - coins[i]];
vector> tmp(combiation[j - coins[i]]);
//在combiation[j - coins[i]]的所有组合基础上都添加一个元素coins[i]
for(auto & t:tmp)
{
t.insert(coins[i]);
}
//将新得到的组合加入到combiation[j]中
for(int k=0;k>amount;
vector coins;
cin.get();//吃掉第一行的'\n'
do
{
int tmp;
cin >> tmp;
coins.push_back(tmp);
} while ((cin.get() != '\n'));
vector> result;
Solution s;
result=s.change(amount,coins);
for (int i = 0; i < result.size(); i++)
{
for (auto tmp:result[i])
{
cout< 相关例题:leetcode39.组合总和