动态规划求解01背包问题
动态规划求解01背包问题
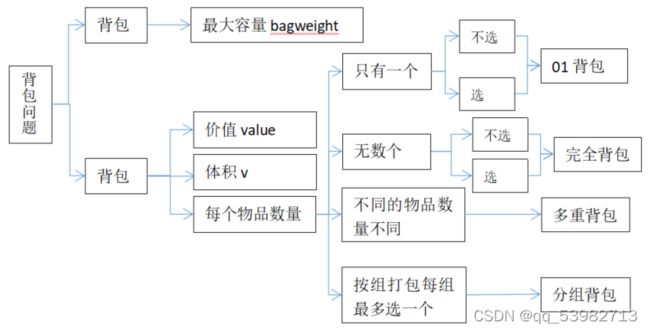
背包问题:首先对于背包问题大家想必都不陌生,这里还是像大家介绍一下何为背包问题?
动态规划求解01背包问题:
有N件物品和一个最多能被重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i]。每件物品只能用一次,求解将那些物品装入背包里的物品价值总和最大。
首先我们来分析一下次题采用暴力解法的时间复杂度。每件物品其实只有两个状,取或不取,所以可以采用回溯法搜索出所有的情况,时间复杂度为O(2^n),n表示物品的数量;无疑暴力解法的时间复杂度过高于是我们可以想到动态规划,经典背包问题几乎都可以使用动态规划解决,我们用如下例子对此算法进行讲解:
背包的最大重量为4
物品信息如下:
| 重量 |
价值 |
|
| 物品0 |
1 |
15 |
| 物品1 |
3 |
20 |
| 物品2 |
4 |
30 |
求背包能背的物品的最大价值是多少?
二维dp数组解决01背包问题:
大家可以是用动态规划五部曲(这是我在网上学习的一个方法):
- 确定dp数组以及下标的含义:
dp[i][j]:表示物品0-i放进背包重量为j的背包中价值总和最大为dp[i][j]
| 背包重量 |
|||||
| 0 |
1 |
2 |
3 |
4 |
|
| 物品0 |
|||||
| 物品1 |
|||||
| 物品2 |
2. 确定递推公式:
在确定递推公式之前我们先思考一下会出现的情况:因为一个物品只会出现两种情况带或者不带,如果带需要考虑此时物品重量weight[i]是否大于等于此时背包重量j如果大于当然不会选择带此物品
- 带此物品发现得到的背包总价值并没有之前所算得的不带此物品的总价值大,于是我们选择不带物品
- 带此物品发现得到的背包总价值比之前不带此物品得到的背包总价值大,所以此时更新dp[i][j],于是我们得到了递推公式:
dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i])
代码如下:
if (j < weight[i]) dp1[i][j] = dp1[i - 1][j];
else dp1[i][j] =max(dp1[i - 1][j], dp1[i - 1][j weight[i]] + value[i]);3. 初始化:
关于初始化,一定要想好在确定初始化,首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],此时无论选哪些物品,背包总价值和一定为0。
| 背包重量 |
|||||
| dp[i][j] |
0 |
1 |
2 |
3 |
4 |
| 物品0 |
0 |
||||
| 物品1 |
0 |
||||
| 物品2 |
0 |
根据递推公式我们可以发现每次遍历下一件物品是否是根据上一件物品的dp[i][j]得到,dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]),dp[i-1][......],i-1即是对上一件物品的情况的获取,于是我们很容易想到此时初始化我们只需要对物品0的情况进行初始化即可。
代码如下:
//初始化
for (int j = weight[0]; j <= bagWeight; j++) {
dp1[0][j] = value[0];
}得到的dp数组如下表
| 背包重量 |
|||||
| dp[i][j] |
0 |
1 |
2 |
3 |
4 |
| 物品0 |
0 |
15 |
15 |
15 |
15 |
| 物品1 |
0 |
||||
| 物品2 |
0 |
4. 确定遍历顺序:
对于二维dp数组的遍历顺序先遍历背包后遍历物品或者先遍历物品后遍历背包均可,当然先遍历物品这里更好理解。
优先遍历物品的代码如下:
//遍历顺序:对于01背包先遍历背包后遍历物品或者现遍历物品后遍历背包均可
for (int i=1; i < weight.size(); i++) {//遍历物品
for (int j = 0; j <= bagWeight; j++) {//遍历背包
}
}为何如此遍历顺序如此呢?如下图所示结合递推公式 dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i])可以很好理解:
| 背包重量 |
|||||
| dp[i][j] |
0 |
1 |
2 |
3 |
4 |
| 物品0 |
0 |
15 |
15 |
15 |
15 |
| 物品1 |
0 |
15 |
15 |
20 |
0 |
| 物品2 |
0 |
15 |
15 |
0 |
0 |
5. 打印dp数组:
| 背包重量 |
|||||
| dp[i][j] |
0 |
1 |
2 |
3 |
4 |
| 物品0 |
0 |
15 |
15 |
15 |
15 |
| 物品1 |
0 |
15 |
15 |
20 |
35 |
| 物品2 |
0 |
15 |
15 |
20 |
35 |
完整C++代码如下:
#include
#include
using namespace std;
vector weight = {1,3,4};
vector value = {15,20,30};
int bagWeight=4;
//动规五部曲
// 1
//定义一个dp[i][j]数组,该数组表示0-(i-1)号物品、背包重量为j时所能存储背包中的最大价值量
//二维数组dp时间复杂度O(i*j),空间复杂度O(i*j)
vector> dp1(weight.size() + 1, vector(bagWeight + 1, 0));
void bagProblem() {
//3
//初始化
for (int j = weight[0]; j <= bagWeight; j++) {
dp1[0][j] = value[0];
}
//4
//遍历顺序:对于01背包先遍历背包后遍历物品或者现遍历物品后遍历背包均可
for (int i=1; i < weight.size(); i++) {//遍历物品
for (int j = 0; j <= bagWeight; j++) {//遍历背包
//2
//递推公式
if (j < weight[i]) dp1[i][j] = dp1[i - 1][j];
else dp1[i][j] = max(dp1[i - 1][j], dp1[i - 1][j - weight[i]] + value[i]);
}
}
cout << "最大价值量:" << endl;
//5
//打印结果
cout << dp1[weight.size() - 1][bagWeight] << endl;
}
//打印dp二维数组背包详情
void printdp1() {
cout << "背包容量";
for (int i = 0; i <= bagWeight; i++)
cout << i << " " << '\t';
cout << endl;
cout << "物品";
cout << endl;
for (int i = 0; i < weight.size(); i++) {
cout << " "<> bagWeight;
bagProblem();
printdp1();
return 0;
} 时间复杂度:O(m*n)----------m-物品的数量-----n-背包的重量
空间复杂度:O(m*n)
一维滚动数组解决01背包问题:
| 重量 |
价值 |
|
| 物品0 |
1 |
15 |
| 物品1 |
3 |
20 |
| 物品2 |
4 |
30 |
为什么会引入一维数组呢?不难发现当我们呢采用二维dp数组解决01背包问题是空间复杂度为O(m*n),我们完全可以采用一维滚动数组优化空间复杂度:
同样动规五部曲:
- 确定dp数组下标及含义:
此时采用滚动数组dp数组定义为dp[j]:容量为j的背包所能容纳物品的最大价值总和
2. 递推公式:
递推公式此时也很好理解 dp[j]=max(dp[j],dp[j-weight[i]]+value[i])即在上一个物品的最大价值总和和加入新物品后价值总和中取最大值
3. 初始化:
要初始化就必须要注意我们的递推公式和题意来进行初始化,因为递推公式采用滚动数组所以此时只需要赋0即可
4. 确定遍历顺序:
代码如下:
for (int i = 0; i < weight.size(); i++) {
for (int j = bagWeight; j >= weight[i]; j--) {
}
}此时滚动数组遍历顺序有所讲究,且此时滚动数组的遍历顺序不可随意改变。为什么呢?
举一个例子,物品0的重量weight[0]=1,价值value[0]=15;
此时如果采用正序遍历
dp[1]=dp[1-weight[0]]+value[0]=15;
dp[2]=dp[2-weight[0]]+value[0]=30;
此时大家不难发现0号物品被使用了两次,这明显与01背包题意相冲突,那么我们如何规避次问题呢?
此时我们不妨试一下倒序遍历,因为倒叙遍历只要物品的重量大于了背包重量,就会根据递归公式进行dp数组赋值并且一个物品只会被使用一次
同样的例子,采用倒序遍历:
dp[2]=dp[2-weight[0]]+value[0]=15;
dp[1]=dp[1-weight[0]]+value[0]=15;
此时刚刚出现的完美的规避了。所以一定注意一维dp数组的遍历顺序一定要使用倒序
5. 打印dp数组:
| 用物品0遍历背包 |
0 |
15 |
15 |
15 |
15 |
| 用物品1遍历背包 |
0 |
15 |
15 |
20 |
35 |
| 用物品2遍历背包 |
0 |
15 |
15 |
20 |
35 |
一维dp数组求解01背包问题完整代码:
#include
#include
using namespace std;
vector weight = {1,3,4};
vector value = {15,20,30};
int bagWeight=4;
vector dp2(bagWeight+1, 0);
void bagProblemOneVector() {
for (int i = 0; i < weight.size(); i++) {
for (int j = bagWeight; j >= weight[i]; j--) {
dp2[j] = max(dp2[j], dp2[j - weight[i]] + value[i]);
}
}
cout << dp2[bagWeight];
}
int main() {
//cout << "请输入您的背包容量" << endl;
//cin >> bagWeight;
bagProblemOneVector();
return 0;
}