机器学习——贝叶斯算法(Bayes)

1、从一个例子来了解贝叶斯？

假设一个学校里面人数总数为U，其中60%的学生为男生，40%的学生为女生，男生全部穿长裤，女生有一半穿长裤一半穿短裤
正向概率：随机选择一个学生，穿长裤的概率和穿裙子的概率分别是多大
逆向概率：迎面走来一个穿长裤的学生，推断其是女生的概率是多大
穿长裤的人数：$U\ast p(boy)\ast p(pants|boy)+U\ast p(girl)\ast p(pants|girl)$
穿长裤的女生人数：$U\ast p(girl)\ast p(pants|girl)$
$$p(girl|pants)=\frac{p(girl)\ast p(pants|girl)}{p(boy)\ast p(pants|boy)+p(girl)\ast p(pants|girl)}$$

2、贝叶斯公式

$$p(A|B)=\frac{p(A)\ast p(B|A)}{p(B)}$$
条件概率：$p(A|B)$，在B发生的条件下A发生的概率
联合概率：$p(A,B)=p(A)\ast p(B|A)$,事件A和事件B都发生的概率

在机器学习的视角下，将A和B分别理解为
A：属于A类别
B：具备B特征
则有$$p(A类别|B特征）=\frac{p(A类别)\ast p(B特征|A类别)}{p(B特征）}$$

假定需要确定2种类别标签，定义为$A_1$和$A_2$，一种放法是计算这两个标签的后验概率的比值
$$\frac{p(A_1类别|B特征）}{p(A_2类别|B特征)}=\frac{p(A_1类别)\ast p(B特征|A_1类别)}{p(A_2类别)\ast p(B特征|A_2类别)}$$

3、朴素贝叶斯分类

朴素贝叶斯法是基于贝叶斯定理，与特征条件独立假设（每个特征独立地对分类结果产生影响）的分类算法,是一种十分简单的分类算法。
朴素贝叶斯就是给你一个输入X，然后通过对之前数据的处理（学习）计算后验概率分布$p(y=C_k|X=x)$,然后将$max(P(y=C_k|X=x))$作为输入X的最大输出类。
通俗地讲：朴素贝叶斯的思想基础是对于给出的待分类项，求解在此项出现的条件下各个类别出现的概率，哪个最大，就认为此待分类项属于哪个类别
朴素贝叶斯定义如下：

1. 假设$x=(a_1,a_2,a_3,\cdots ,a_m)$是一个待分类项，$a_i$是$x$的特征属性,即共有$m$个特征属性
2. 有类别集合$c=(y_1,y_2,\cdots ,y_n)$,即目标类别共有$n$种
3. 计算$p(y_1|x),p(y_2|x),\cdots ,p(y_n|x)$
4. 如果$p(y_k|x)=\max \{p(y_1|x),p(y_2|x),\cdots ,p(y_n|x)\}$,则$x\in y_k$

难点在于如何计算第三步中的条件概率，方法如下：
根据贝叶斯公式有$$p(y_i|x)=\frac{p(x|y_i)\ast p(y_i)}{p(x)}$$
由于贝叶斯算法假设各特征属性是独立的，则有：
$$p(x|y_i)=p(a_1|y_i)\ast p(a_2|y_i)\ast \cdots \ast p(a_m|y_i)=\prod _{j=1}^{m}p(a_j|y_i)$$
因为分母对于所有类别是一样的，因为我们只要将分子最大化即可。即求：
$$\max \{p(y_i)\ast \prod _{j=1}^{m}p(a_j|y_i)\}$$
朴素贝叶斯分类流程图：

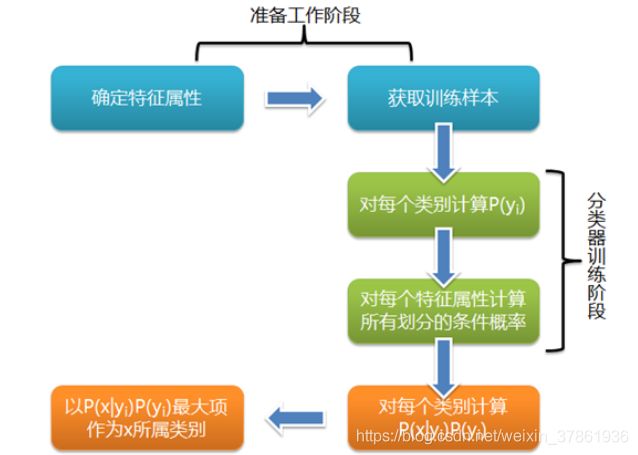
4、三种朴素贝叶斯模型

高斯朴素贝叶斯
当处理连续的特征变量时，应该采用高斯朴素贝叶斯模型。
高斯朴素贝叶斯假设每一个标签数据都服从简单的高斯分布，需使用概率密度函数进行计算。
假定$p(a_j|y_i)$服从高斯分布$N\sim ({\mu }_{ij},{\sigma }_{ij}^2)$
${\mu }_{ij}$:第$i$个类别在第$j$个特征上取值的均值
${\sigma }_{ij}^2$:第$i$个类别在第$j$个特征上取值的方差
则$p(a_j|y_i)$的概率密度函数为：
$$p(a_j|y_i)=\frac{1}{\sqrt{2\pi }{\sigma }_{ij}}{e}^{-\frac{(a_j-{\mu }_{ij}{)}^2}{2{\sigma }_{ij}^2}}$$
多项式朴素贝叶斯
当特征是离散的时候，使用多项式朴素贝叶斯模型。
多项式朴素贝叶斯模型在计算先验概率和条件概率时会做一些平滑处理，关于平滑处理将在第6节拉普拉斯修正(Laplacian correction)中讲解。

5、西瓜书上关于朴素贝叶斯的例子

假设我们的任务是根据一个西瓜的特征来在它被吃之前判断它是否是个好瓜。数据集如下：

基于上面已有的数据，我们想利用朴素贝叶斯算法训练出一个分类器，以判断一个具有特征{色泽=青绿，根蒂=蜷缩，敲声=浊响，纹理=清晰，脐部=凹陷，触感=硬滑，密度=0.697，含糖率=0.460}的测试样例瓜是否为好瓜。
首先计算先验概率$p(y_i)$，$y_i$代表类别，这里就两类，好瓜和坏瓜：
$p(好瓜=是）=\frac{8}{17}\approx 0.471$
$p(好瓜=否）=\frac{9}{17}\approx 0.529$
然后计算每个属性值的条件概率$p(a_j|y_i)$:
对于离散值有：

对于连续值有（这里认为连续值属性服从高斯分布）：

最后，我们计算测试瓜分别属于好瓜和坏瓜的概率：

因此朴素贝叶斯分类器将测试样本判别为"好瓜"。

6、拉普拉斯修正(Laplacian correction)

如果某个离散类型的特征$a_k$的某个取值在训练集中没有与类$y_i$同时出现过,但是其他特征的取值都非常符合类$y_i$,那么在计算后验概率$p(y_i|x)$时，就会因条件概率$p(a_k|y_i)=0$导致分类器认为该样本属于类别$y_i$的概率为0，这显然是不合理的。
例如：
在上面的西瓜训练集中，好瓜当中暂时没有具备特征{敲声=清脆}的样本，于是对于一个“敲声=清脆”的测试例，尽管其他属性值明显像是好瓜，这个样本都会被分类器判定为是好瓜的概率为0。
拉普拉斯修正就是为了解决这样的问题。
拉普拉斯修正的具体做法为：
令$N$表示训练集$D$中可能的类别数，$N_j$表示第$j$个属性可能的取值数，那么我们估计类别先验概率$p(y_i)$和离散属性条件概率$p(a_j|y_i)$的两个公式分别被调整为：
$$p(y_j)=\frac{|D_{yi}|+1}{|D|+N}$$
$$p(a_j|y_i)=\frac{|D_{y_i{a}_j}|+1}{|D_{y_i}|+N_j}$$
这就保证了即使存在某个属性$a_j$的取值未曾与类别$y_i$同时出现过，我们也不会把其概率$P(a_j|y_i)$算成0

在上面的西瓜数据集中，使用拉普拉斯修正后，对于类别概率和条件概率有：


拉普拉斯修正避免了因训练集样本不充分而导致概率估值为零的问题，并且在训练集变大时，修正过程所引入的先验(prior) 的影响也会逐渐变得可忽略，使得估值渐趋向于实际概率值。

参考链接：http://www.luyixian.cn/news_show_3477.aspx