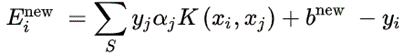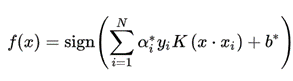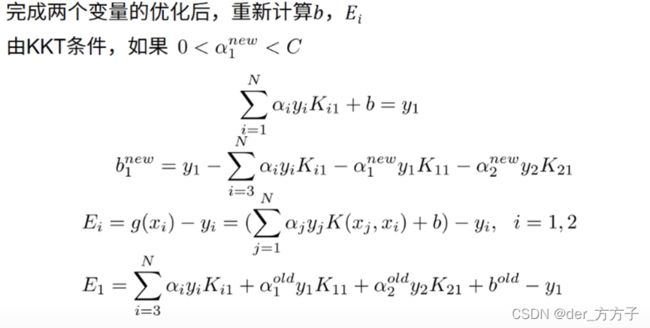机器学习 SMO算法breast_cancer数据集分类
一、实验原理
1、序列最小最优化SMO算法：
（1）通过满足KKT条件，来求解；
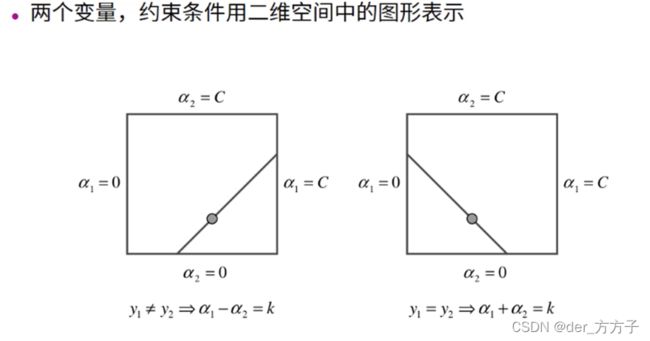
（2）如果没有满足KKT条件，选择两个变量，固定其他变量，构造二次规划问题。
优化目标：
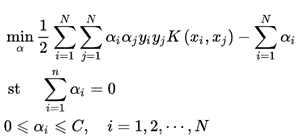
变量是拉格朗日乘子，一个变量a_i对应于一个样本点(x_i,y_i); 变量的总数等于训练样本的容量N。 SMO是启发式算法，思路是： 固定其他变量，针对其中两个变量构建二次规划问题，通过子问题求解，提高算法计算速度。 这两个变量，一个是违反KKT条件最严重的那个，另一个是由约束条件自动确定。
2、算法步骤
SMO算法在每个子问题中选择两个变量优化，其中至少一个变量是违反KKT条件的。
（1）第一个变量选择 从间隔边界上的支持向量点（0
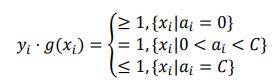
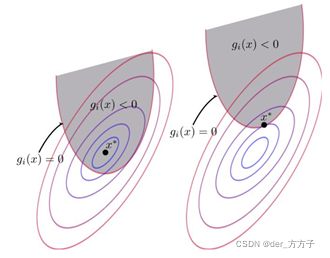
（2）第二个变量选择使得|E_1-E2|最大。其中， 代表函数 g(x)对输入x_i的预测值与真实输出y_i之差。
（3）计算阈值b 和差值E_i
（4）根据决策函数进行预测可获得样本标签
SVM问题求解
坐标下降
新的子问题
优化成只有两个变量的目标函数
确定解析解的上下界
第一种情况
a1-a2=k
a1+a2=k,同理
求解过程
a的最终解
由kkt条件计算得出b,Ei
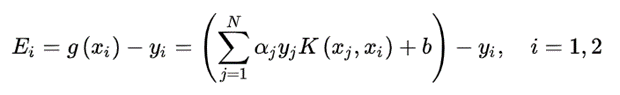
二、实验对象
数据集名称：breast_cancer
数据集属性：UCI乳腺癌数据（30个特征值）
任务：SVM二分类
数据集划分：训练集：测试集 =7:3
三、实验代码
from sklearn import datasets
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
class SVM:
def __init__(self, max_iter=100, kernel='linear'):
self.max_iter = max_iter
self._kernel = kernel
def initialize_parameters(self, data, labels):
#初始化参数
#找出特征维度，shape返回元组
#m，n返回样本数与特征数
self.m, self.n = data.shape
self.X = data
self.Y = labels
self.b = 0.0
# 初始化拉格朗日乘子
self.alpha = np.ones(self.m)
#E为函数g(x)对输入xi的预测值与真实值yi之差
#
self.E = [self._E(i) for i in range(self.m)]
# 松弛变量，即允许分类出错的代价
self.C = 0.6
def KKT(self, i):
#KKT条件函数
'''
SMO算法在每个子问题中选择两个变量优化，其中至少一个变量是违反KKT条件的。
（1）第一个变量选择 从间隔边界上的支持向量点
（2）第二个变量的选择 第二个变量选择使得|E1-E2|最大
'''
# 对应KKT的式子
y_g = self._g(i) * self.Y[i]
if self.alpha[i] == 0:
return y_g >= 1
elif 0 < self.alpha[i] < self.C:
return y_g == 1
else:
return y_g <= 1
# g(x)预测值，输入xi（X[i]）
def _g(self, i):
r = self.b
for j in range(self.m):
#拉格朗日乘子*训练集的真实标签 预测样本，训练集特征
r += self.alpha[j] * self.Y[j] * self.kernel(self.X[i], self.X[j])
return r
# 核函数
def kernel(self, x1, x2):
if self._kernel == 'linear':
#线性核函数
return sum([x1[k] * x2[k] for k in range(self.n)])
elif self._kernel == 'poly':
#多项式核函数
return (sum([x1[k] * x2[k] for k in range(self.n)]) + 1)**2
return 0
def _E(self, i):
#E（x）为g(x)对输入x的预测值和y的差
#E_i = g(x_i) - y_i
return self._g(i) - self.Y[i]
#启发式选择机制
def _init_alpha(self):
#外层循环首先遍历所有满足0
#因此每一次调整更新会带来最大的合理更新
index_list = [i for i in range(self.m) if 0 < self.alpha[i] < self.C]
#当a=C的时候优先优化分割边界上的点，每一次能有一个更大的调整变化
non_satisfy_list = [i for i in range(self.m) if i not in index_list]
index_list.extend(non_satisfy_list)
# 外层循环选择满足0
for i in index_list:
#内层循环的标准是希望能使目标函数有足够大的变化
#每次调整得越多越好，目标函数调整得越快越好
if self.KKT(i):
continue
# 因此内层循环，要使|E1-E2|最大化
E1 = self.E[i]
# 如果E1是+，选择最小的E_i作为E2；如果E1是负的，选择最大的E_i作为E2
if E1 >= 0:
j = min(range(self.m), key=lambda x: self.E[x])
else:
j = max(range(self.m), key=lambda x: self.E[x])
return i, j
def _compare(self, _alpha, L, H):
if _alpha > H:
return H
elif _alpha < L:
return L
else:
return _alpha
def fit(self, data, labels):
#模型训练
#初始化参数
self.initialize_parameters(data, labels)
#定义最大迭代次数
for _ in range(self.max_iter):
i1, i2 = self._init_alpha()
# 边界,计算阈值b和差值E_i
if self.Y[i1] == self.Y[i2]:
# L = max(0, alpha_2 + alpha_1 -C)
# H = min(C, alpha_2 + alpha_1)
L = max(0, self.alpha[i1] + self.alpha[i2] - self.C)
H = min(self.C, self.alpha[i1] + self.alpha[i2])
else:
# L = max(0, alpha_2 - alpha_1)
# H = min(C, alpha_2 + alpha_1+C)
L = max(0, self.alpha[i2] - self.alpha[i1])
H = min(self.C, self.C + self.alpha[i2] - self.alpha[i1])
#
E1 = self.E[i1]
E2 = self.E[i2]
# eta=K11+K22-2K12= ||phi(x_1) - phi(x_2)||^2
eta = self.kernel(self.X[i1], self.X[i1]) + self.kernel(self.X[i2],self.X[i2])
- 2 * self.kernel(self.X[i1], self.X[i2])
if eta <= 0:
# print('eta <= 0')
continue
# 更新约束方向的解
alpha2_new_unc = self.alpha[i2] + self.Y[i2] * (E1 - E2) / eta
alpha2_new = self._compare(alpha2_new_unc, L, H)
alpha1_new = self.alpha[i1] + self.Y[i1] * self.Y[i2] * (
self.alpha[i2] - alpha2_new)
b1_new = -E1 - self.Y[i1] * self.kernel(self.X[i1], self.X[i1]) * (
alpha1_new - self.alpha[i1]) - self.Y[i2] * self.kernel(
self.X[i2],
self.X[i1]) * (alpha2_new - self.alpha[i2]) + self.b
b2_new = -E2 - self.Y[i1] * self.kernel(self.X[i1], self.X[i2]) * (
alpha1_new - self.alpha[i1]) - self.Y[i2] * self.kernel(
self.X[i2],
self.X[i2]) * (alpha2_new - self.alpha[i2]) + self.b
if 0 < alpha1_new < self.C:
b_new = b1_new
elif 0 < alpha2_new < self.C:
b_new = b2_new
else:
# 选择中点
b_new = (b1_new + b2_new) / 2
# 更新参数
self.alpha[i1] = alpha1_new
self.alpha[i2] = alpha2_new
self.b = b_new
#重新计算误差
self.E[i1] = self._E(i1)
self.E[i2] = self._E(i2)
return 'train done!'
def predict(self, data):
r = self.b
for i in range(self.m):
r += self.alpha[i] * self.Y[i] * self.kernel(data, self.X[i])
return 1 if r >= 0 else -1
def score(self, X_test, y_test):
#计算模型准确率
right_count = 0
for i in range(len(X_test)):
result = self.predict(X_test[i])
#print(result, ", ", y_test[i])
if result == y_test[i]:
right_count += 1
#把真实值与预测值做比较，返回模型的准确率
return right_count / len(X_test)
def get_datasets():
#获取数据
x, y = datasets.load_breast_cancer(return_X_y=True)
# 归一化
std = StandardScaler()
X_norm = std.fit_transform(x)
X_train = X_norm[:int(len(X_norm)*0.7)]
X_test = X_norm[int(len(X_norm)*0.7):]
y_train = y[:int(len(X_norm)*0.7)]
y_test = y[int(len(X_norm)*0.7):]
y_train[y_train == 0] = -1
y_test[y_test == 0] = -1
return X_train,y_train,X_test,y_test
if __name__ == '__main__':
X_train,y_train,X_test,y_test = get_datasets()
svm = SVM(max_iter=30)
svm.fit(X_train, y_train)
print("acccucy:{:.4f}".format(svm.score(X_test, y_test)))
四、实验结果
模型准确率为97.08%
在实现SMO算法过程中，查阅了很多资料也学习了别人的很多优秀代码，但是这个程序的准确率并非一开始就能达到97%，最开是的准确率在64%左右。经过对函数、数据格式的不断优化才到达了现在的效果。尽管如此，对于支持向量机依然似懂非懂，只可意会，以下是经过本次实验粗浅的认识和收获作为实验总结。