听说你还不会归并排序？

作者 | 张琼芳

不忘初心，方得始终

归并排序 MergeSort 是在计算机上实现的最早的算法之一， 由冯·诺伊曼 John von Neumann 在 1945 年发表" 101 报告"时提出，后在 1951 年完成的 EDVAC 计算机上应用了这一算法。

归并排序是在归并的基础上将数组不断划分成子数组进行排序，从而使整个数组完全有序，该算法是采用了典型的分治法来解决问题，即先将问题分解成子问题，再对子问题的解进行合并从而得到整个问题的解。

归并排序的核心思想就在于 并（merging），为了更好的理解归并排序，我们先来了解一下原地归并的概念。

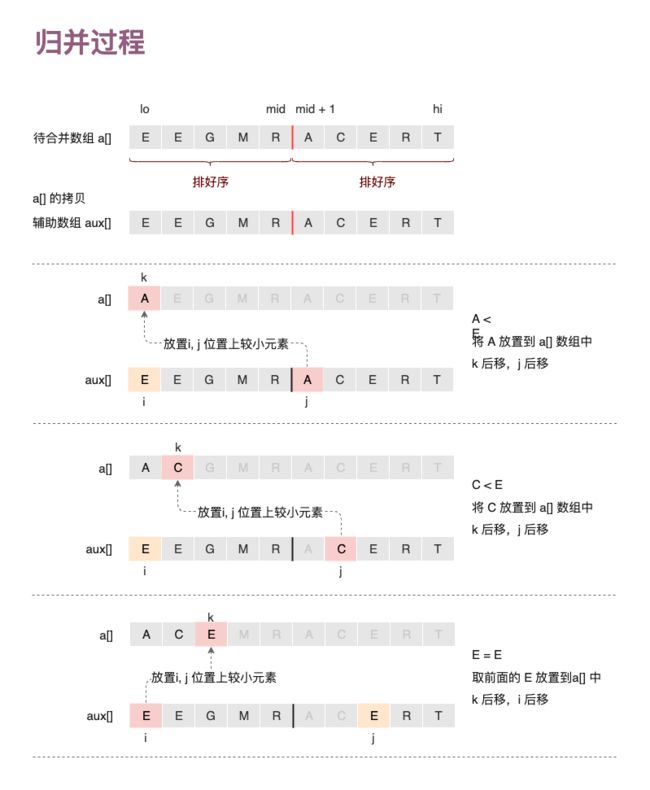
归并过程

1. 新建一个原始数组的拷贝作为辅助数组；

2. 使用两个指针同时遍历辅助数据中的两部分数据；

3. 将两个指针指向的较小元素放置到原始数组中；

4. 然后将较小元素的指针往后一位；

5. 当有一边数据遍历完成，直接剩下的那部分数据拷贝到原始数组中；

代码实现

private static void merge(Comparable[] a, Comparable[] aux, int lo, int mid, int hi) {
    assert isSorted(a, lo, mid);
    assert isSorted(a, mid + 1, hi);
    for (int k = lo; k <= hi; k++) {
        aux[k] = a[k];
    }

    int i = lo, j = mid + 1;
    for (int k = lo; k <= hi; k++) {
        if (i > mid) a[k] = aux[j++]; // 左边耗尽，取右半边数据
        else if (j > hi) a[k] = aux[i++]; // 右边耗尽，取左半边数据
        else if (less(aux[i], aux[j])) a[k] = aux[j++]; // 取较小值
        else a[k] = aux[i++];
    }
    assert isSorted(a, lo, hi);
}

public static boolean less(Comparable v, Comparable w) {
    return v.compareTo(w) < 0;
}

public static boolean isSorted(Comparable[] a, int lo, int hi) {
    for (int i = lo + 1; i <= hi; i++) {
         if (less(a[i], a[i-1])) return false;
    }
    return true;
}

public static boolean isSorted(Comparable[] a) {
    return isSorted(a, 0, a.length - 1);
}

这里代码用到了 assert，顺便提一下

断言 Assertions

我们可以使用断言来验证猜想，前面的代码里我们使用 assert 来判定输入参数是否如我们所预想的那样已经排好序

1. 断言可以帮助我们检测逻辑上的 bug

2. 让代码可读性更强 如果 assert 后面的条件语句不满足，则会抛出异常

我们可以加上参数来控制异常的抛出，在部署代码到生产环境时禁用断言，而在本地或者测试环境启用断言来帮助我们调试程序，默认是禁用的，我们需要手动开启

java -ea MyApplication // 启用断言 enable
java -da MyApplication // 禁用断言 disable （默认设置）

如果使用 IDEA 的话在 Application 的 VM Options 中加上 -ea 就可以开启了，不填默认是禁用的

归并过程完成了，我们有两种方式可以实现排序算法

自顶向下排序

将数组元素不断二分，直到子数组元素只有一个，然后将两个有序的数组向下合并，再将新的两个有序的数组向下合并，直至整个数组有序。

我们只需要递归的将数据不断分区合并就可以达到排序的效果了，代码如下：

public class MergeSort {
    private static void merge(Comparable[] a, Comparable[] aux, int lo, int mid, int hi) {
	/** 见前面归并部分 */
    }

    private static void sort(Comparable[] a, Comparable[] aux, int lo, int hi) {
        if (hi <= lo) return;
        int mid = lo + (hi - lo) / 2;
        sort(a, aux, lo, mid);
        sort(a, aux, mid + 1, hi);
        merge(a, aux, lo, mid, hi);
    }

    private static void sort(Comparable[] a) {
        Comparable[] aux = new Comparable[a.length];
        sort(a, aux, 0, a.length - 1);
    }
}

这里有个小细节，辅助数组 aux 是在入口的 sort() 方法中初始化的，而不是放在递归的方法里，因为放在递归的方法里会产生很多额外的小数组，会导致内存比较碎，不利于内存的回收整理，而放在外面只需要初始化一个数组就可以了，如果你的归并排序性能比较差一般都是因为这个引起的。

归并排序是典型的分治思想的实践，将问题分解成子问题，各个击破，然后将结果合并。

自底向上排序

将数组中元素一个个归并成两两有序的子数组，再归并成 2 个，再归并成 8 个直至数组完全有序。

数组是按照长度进行划分的，最后子数组的数量可能不满足要求，不能超过数据最大长度，需要特殊处理一下。

private static void sortByBottomUp(Comparable[] a) {
    int N = a.length;
    Comparable[] aux = new Comparable[N];
    for (int size = 1; size < N; size = size + size) 
        for (int lo = 0; lo < N - size; lo += size + size) 
            merge(a, aux, lo, lo + size + 1, Math.min(lo + size + size - 1, N - 1));
    
}

性能分析

归并排序在数据量非常大的情况下性能是很好的，比插入排序快很多。

运行效率

• 个人 PC：   次比较/秒

• 超级 PC：    次比较/秒

所以一个好的算法可以强过超级 PC，简而言之可以省钱。

时间复杂度

归并排序的时间复杂度为    ，因为每次都将数组分为两部分，然后进行合并

  ⎡ ⎤ ⎣ ⎦  

// 证明过程

   

   

   

   

   

. . .

   

   

   

空间复杂度

我们在排序时借助了一个与原数组空间相等的数组，所以空间复杂度为    。

稳定排序

归并排序是稳定排序，在排序时本来排在前面的元素不会在排序过程中调换到后面，所以是稳定排序。

排序最佳实践

归并排序比较适合大数组，对于较小数组，使用插入排序性能比较好，我们在做排序时可以设置一个阈值，当大于这个值的时候我们就使用归并排序，否则我们使用插入排序，这个阈值约为 7。并且我们在合并前可以先进行检测，如果已经是有序的，则可以直接 return 了。

代码实现

private static void sort(Comparable[] a, Comparable[] aux, int lo, int hi) {
    if (hi <= lo + CUTOFF - 1) {
        Insertion.sort(a, lo, hi);
        return;
    }
    int mid = lo + (hi - lo) / 2;
    sort (a, aux, lo, mid);
    sort (a, aux, mid+1, hi);
    if (!less(a[mid+1], a[mid])) return; // 有序则直接 return
    merge(a, aux, lo, mid, hi);
}

扩展

Java 集合类中提供的排序方法 Collections.sort() 也是复合实现，在数据量小的时候使用插入排序，里面的阈值是 32，但是它实现的插入排序方法有优化过，是二分插入排序。

感兴趣的同学可以看看 Collections.sort() 方法的源码，里面涉及到了各种不同的排序算法。

参考资料

• 算法第四版：https://book.douban.com/subject/19952400/

• Algorithms, PartI, MergeSort：https://www.coursera.org/lecture/algorithms-part1/mergesort-ARWDq

全文完

---

以下文章您可能也会感兴趣：

• WePY 2.0 新特性

• SSL证书的自动化管理

• 了解一下第三方登录

• 分布式 ID 生成策略

• 单元测试的实践之路

• 可线性化检查：与 NP 完全问题做斗争
  

• Java 类型系统从入门到放弃
  

• Webpack 快速上手（下）
  

• Webpack 快速上手（中）
  

• Webpack 快速上手（上）

• Airbnb 的 React Native 之路（下）

• Airbnb 的 React Native 之路（上）
  

• 零基础玩转 Serverless

• iOS 开发：深入理解 Xcode 工程结构（一）

我们正在招聘 Java 工程师，欢迎有兴趣的同学投递简历到 [email protected] 。