【机器学习】SVM算法

 

目录

什么是SVM 

 SVM 基本概念

SVM相关问题 

SVM算法原理

点到超平面的距离公式

最大间隔的优化模型

松弛变量

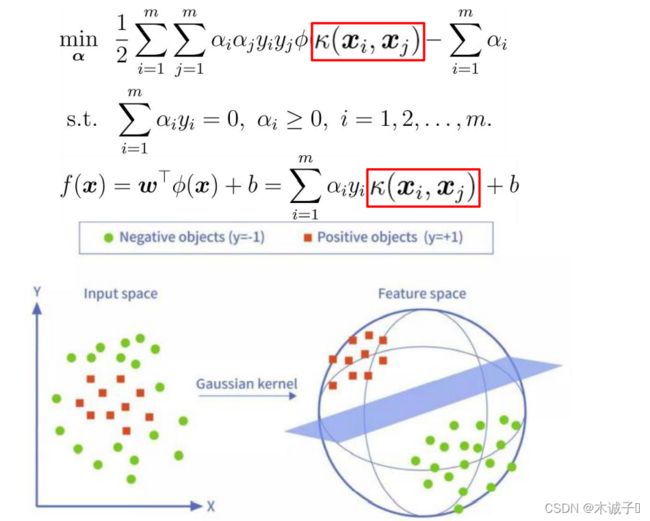
核函数：线性不可分—高维可分

SVM实现对鸢尾花数据集的二分类 

数据集详情

SVM算法svm.py

测试模型main.py

运行结果

​

 SVM总结

---

什么是SVM 

        SVM （support vector machines）即支持向量机。它是一种二分类模型，它将实例的特征向量映射为空间中的一些点，SVM 的目的就是想要画出一条线，以 “最好地” 区分这两类点，以至如果以后有了新的点，这条线也能做出很好的分类。SVM 适合中小型数据样本、非线性、高维的分类问题。                                                                                                                                                                                                                                    SVM 最早是由 Vladimir N. Vapnik 和 Alexey Ya. Chervonenkis 在1963年提出，目前的版本（soft margin）是由 Corinna Cortes 和 Vapnik 在1993年提出，并在1995年发表。深度学习（2012）出现之前，SVM 被认为机器学习中近十几年来最成功，表现最好的算法。

 SVM 基本概念

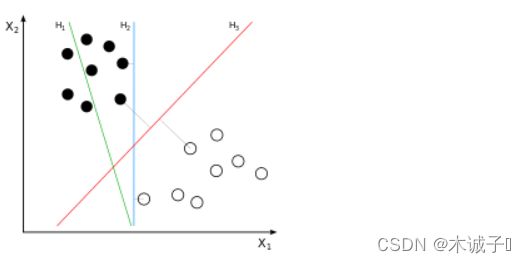
        将实例的特征向量（以二维为例）映射为空间中的一些点，如下图的实心点和空心点，它们属于不同的两类。SVM 的目的就是想要画出一条线，以“最好地”区分这两类点，以至如果以后有了新的点，这条线也能做出很好的分类。

SVM相关问题 

能够画出多少条线对样本点进行区分？

答：线是有无数条可以画的，区别就在于效果好不好，每条线都可以叫做一个划分超平面。比如上面的绿线就不好，蓝线还凑合，红线看起来就比较好。我们所希望找到的这条效果最好的线就是具有 “最大间隔的划分超平面”。

为什么要叫作“超平面”呢？

答：因为样本的特征很可能是高维的，此时样本空间的划分就不是一条线了。

画线的标准是什么？/ 什么才叫这条线的效果好？/ 哪里好？

答：SVM 将会寻找可以区分两个类别并且能使间隔（margin）最大的划分超平面。比较好的划分超平面，样本局部扰动时对它的影响最小、产生的分类结果最鲁棒、对未见示例的泛化能力最强。

间隔（margin）是什么？

答：对于任意一个超平面，其两侧数据点都距离它有一个最小距离（垂直距离），这两个最小距离的和就是间隔。比如下图中两条虚线构成的带状区域就是 margin，虚线是由距离中央实线最近的两个点所确定出来的（也就是由支持向量决定）。但此时 margin 比较小，如果用第二种方式画，margin 明显变大也更接近我们的目标。
                                

 为什么要让 margin 尽量大？

答：因为大 margin 犯错的几率比较小，也就是更鲁棒啦。

支持向量是什么？

答：从上图可以看出，虚线上的点到划分超平面的距离都是一样的，实际上只有这几个点共同确定了超平面的位置，因此被称作 “支持向量（support vectors）”，“支持向量机” 也是由此来的。

SVM算法原理

点到超平面的距离公式

         既然这样的直线是存在的，那么我们怎样寻找出这样的直线呢？与二维空间类似，超平面的方程也可以写成一下形式：

                                        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

         有了超平面的表达式之后之后，我们就可以计算样本点到平面的距离了。假设为样本的中的一个点，其中表示为第个特征变量。那么该点到超平面的距离就可以用如下公式进行计算：

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

 其中||W||为超平面的范数，常数b类似于直线方程中的截距。

最大间隔的优化模型

        现在我们已经知道了如何去求数据点到超平面的距离，在超平面确定的情况下，我们就能够找出所有支持向量，然后计算出间隔margin。每一个超平面都对应着一个margin，我们的目标就是找出所有margin中最大的那个值对应的超平面。因此用数学语言描述就是确定w、b使得margin最大。这是一个优化问题其目标函数可以写成 ：
        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

        其中y表示数据点的标签，且其为-1或1。距离用计算，这是就能体会出-1和1的好处了。如果数据点在平面的正方向(即+1类)那么是一个正数，而当数据点在平面的负方向时(即-1类)，依然是一个正数，这样就能够保证始终大于零了。注意到当w和b等比例放大时，d的结果是不会改变的。因此我们可以令所有支持向量的u为1，而其他点的u大1这是可以办通过调节w和b求到的。因此上面的问题可以简化为： 

                                                                                 

 为了后面计算的方便，我们将目标函数等价替换为：

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

 这是一个有约束条件的优化问题，通常我们可以用拉格朗日乘子法来求解,应用拉格朗日乘子法如下：

 ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​            公式1

 求L关于求偏导数得:

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​                                公式2

 将公式2代入到公式1中化简得：

 ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

  该对偶问题的KKT条件为：

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​  

   到此，似乎问题就能够完美地解决了。但是这里有个假设：数据必须是百分之百可分的。但是实际中的数据几乎都不那么“干净”，或多或少都会存在一些噪点。为此下面我们将引入了松弛变量来解决这种问题。

松弛变量

         由上一节的分析我们知道实际中很多样本数据都不能够用一个超平面把数据完全分开。如果数据集中存在噪点的话，那么在求超平的时候就会出现很大问题。从图三中课看出其中一个蓝点偏差太大，如果把它作为支持向量的话所求出来的margin就会比不算入它时要小得多。更糟糕的情况是如果这个蓝点落在了红点之间那么就找不出超平面了。

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​​​​​​​​

 因此引入一个松弛变量ξ来允许一些数据可以处于分隔面错误的一侧。这时新的约束条件变为:

 ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

 式中ξi的含义为允许第i个数据点允许偏离的间隔。如果让ξ任意大的话，那么任意的超平面都是符合条件的了。所以在原有目标的基础之上，我们也尽可能的让ξ的总量也尽可能地小。所以新的目标函数变为：

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​         

 其中的C是用于控制“最大化间隔”和“保证大部分的点的函数间隔都小于1”这两个目标的权重。将上述模型完整的写下来就是：

 ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

新的拉格朗日函数变为：

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​         

 接下来将拉格朗日函数转化为其对偶函数，首先对分别求ξ的偏导，并令其为0,结果如下：

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

代入原式化简之后得到和原来一样的目标函数：

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​         

但是由于我们得到而，因此有所以对偶问题写成： 

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

 经过添加松弛变量的方法，我们现在能够解决数据更加混乱的问题。通过修改参数C，我们可以得到不同的结果而C的大小到底取多少比较合适，需要根据实际问题进行调节。 

核函数：线性不可分—高维可分

 

SVM实现对鸢尾花数据集的二分类 

数据集详情

鸢尾花(iris)数据集， 数据集内包含 3 类共 150 条记录，每类各 50 个数据， 每条记录都有 4 项特征：花萼长度、花萼宽度、花瓣长度、花瓣宽度，可以通过这4个特征预测鸢尾花卉属于（iris-setosa, iris-versicolour, iris-virginica）中的哪一品种。 这里只取前100条记录，两项特征，两个类别。

SVM算法svm.py

import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

def create_data():
    iris = load_iris()
    df = pd.DataFrame(iris.data, columns=iris.feature_names)
    df['label'] = iris.target
    df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
    data = np.array(df.iloc[:100, [0, 1, -1]])
    for i in range(len(data)):
        if data[i,-1] == 0:
            data[i,-1] = -1
    return data[:,:2], data[:,-1]
#使用RBF(Radial basis function)核函数处理
def K(x,z,sigma=1.5):
    return np.exp(np.dot((x-z),(x-z).T)/-(2*sigma**2))
#对应课本147页的g(x_i)，该函数助于验证KKT条件
def g(i,x,y,alpha,b):
    sum=b
    for j in range(len(y)):
        sum+=alpha[j]*y[j]*K(x[i],x[j])
    return sum
#验证第i个样本点是否满足KKT条件
def isKKT(alpha,i,x,y,b,C):
    if alpha[i]==0 and y[i]*g(i,x,y,alpha,b)>=1:
        return True
    elif alpha[i]==C and y[i]*g(i,x,y,alpha,b)<=1:
        return True
    elif alpha[i]>0 and alpha[i]

测试模型main.py

from functions import *
from numpy import *
from random import *
from matplotlib import pyplot as plt
def train(C=1.0):
    #获得数据集
    x,y=create_data()
    #设定迭代次数为100次
    iter=100
    #样本容量也就是标签的个数
    N=len(y)
    #alpha的初始值取全0
    alpha=zeros(len(y))
    #设置i,j的初始值（对应alpha1和alpha2）
    i,j=randint(0,N-1),randint(0,N-1)
    #保证i≠j
    while i==j:
        i=randint(0,N-1)
    for k in range(iter):
        #x的尺寸为一个1×2行向量
        x_i,x_j=x[i],x[j]
        #y的取值为+1或-1
        y_i,y_j=y[i],y[j]
        #计算ita，为计算a2_newunc做准备
        ita=K(x_i,x_i)+K(x_j,x_j)-2*K(x_i,x_j)
        if ita==0:
            continue
        #计算分割平面参数w与b
        #x:100×2矩阵，w：1×2矩阵
        #由于y-dot(w,x.T)是个与y等长的行向量，取其各元素平均值
        w=dot(alpha*y,x)
        b=mean(y-dot(w,x.T))
        #计算误差E1和E2
        E_i=E(w,b,x_i,y_i)
        E_j=E(w,b,x_j,y_j)
        #计算a2_ewunc
        a1_old=alpha[i]
        a2_old=alpha[j]
        a2_newunc=a2_old+y_j*(E_i-E_j)/ita
        #计算L与H
        L,H=0.0,0.0
        if y_i!=y_j:
            L=max(0,a2_old-a1_old)
            H=min(C,C+a2_old-a1_old)
        elif y_i==y_j:
            L=max(0,a2_old+a1_old-C)
            H=min(C,a2_old+a1_old)
        #计算剪辑后a2_new与a1_new的值
        a2_new=max(L,min(H,a2_newunc))
        a1_new=a1_old+y_i*y_j*(a2_old-a2_new)
        #更新alpha
        alpha[i],alpha[j]=a1_new,a2_new
        #violation表示每个元素违反KKT条件的程度
        violation=zeros(N)
        #对每一个样本点检验KKT条件，在violation内记录每个样本点违反KKT的程度
        for k in range(N):
            if isKKT(alpha,k,x,y,b,C)==False:
                violation[k]=float(vioKKT(alpha,k,x,y,b))
            #如果没有违反KKT条件，则违反程度是0
            else:
                violation[k]=0.0
        #找到violation中违反程度最大的点，设定为i，对应alpha_1
        i=findindex(violation,max(violation))
        #这里设置j（对应alpha_2）为不等于i的随机数。
        #原本alpha_2的选取应该是令abs(E_i-E_k)最大的k值对应的alpha点
        #经过测试，在大多数情况下，abs(E_i-E_k）(1×100向量)的所有元素都是0
        #即预测每个元素都准确，每个元素的分类误差都是0，误差的差值也是0
        #只有少数情况下，会有一个误差差值不等于0
        #对于前一种情况，无所谓“最大的误差差值”（因为都是0），因此只能设置j为随机数
        #对于后一种情况，由于出现的次数少，并且那一个不为0的差值的元素出现的位置具有随机性
        #因此总是将j设定为随机数
        j=randint(0,N-1)
        while j==i:
            j = randint(0, N - 1)
    #计算最终（迭代100次）分割平面参数
    w = dot(alpha * y, x)
    b = mean(y - dot(w, x.T))
    draw_x, draw_y, draw_label = [], [], []
    #在散点图上标记样本点的位置，样本点第一个元素作为x坐标，第二个元素作为y坐标
    for p in x:
        draw_x.append(p[0])
        draw_y.append(p[1])
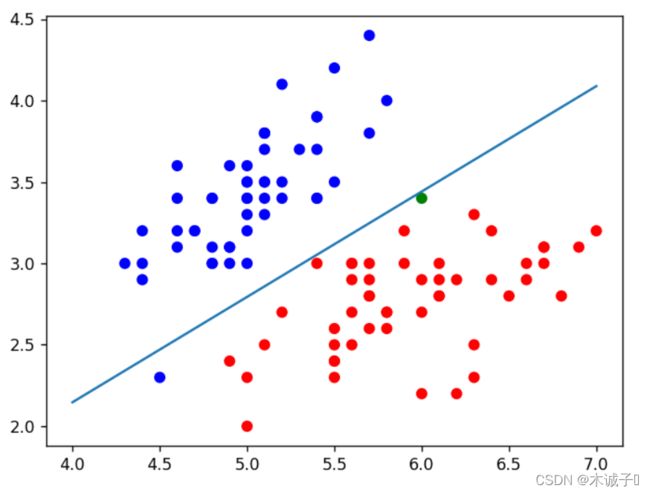
    #画散点图，其中支持向量呈现绿色，正类呈现红色，负类呈现蓝色
    #样本点离分割直线最近的为支持向量
    distance=zeros(len(y))
    for i in range(len(y)):
        distance[i]=distance_count(x[i],w,b)
    vector=findindex(distance,min(distance))
    for i in range(len(y)):
        if i==vector:
            draw_label.append('g')
        else:
            if y[i] > 0:
                draw_label.append('r')
            else:
                draw_label.append('b')
    plt.scatter(draw_x, draw_y, color=draw_label)
    plain_x = range(4, 8, 1)
    plain_y = []
    for i in plain_x:
        temp = double(-(w[0] * i + b) / w[1])
        plain_y.append(temp)
    plt.plot(plain_x, plain_y)
    #最终绘图
    plt.savefig('SMO.jpg')
    plt.show()
if __name__ == '__main__':
    train()

运行结果

 

 SVM总结

• 支持向量机（SVM）是一种有监督学习算法，不仅可以用于分类问题，也可用于回归问题
• 支持向量机理论的优点：对于含有大量特征属性的小样本有很强的鲁棒性、对于简单和复杂的分类模型都有很强的学习能力、如果采用复杂的数学模型可以避免过拟合现象
• 训练好的模型的算法复杂度是由支持向量的个数决定的，而不是由数据的维度决定的。所以 SVM 不太容易产生 overfitting。
• SVM 训练出来的模型完全依赖于支持向量，即使训练集里面所有非支持向量的点都被去除，重复训练过程，结果仍然会得到完全一样的模型。
• 一个 SVM 如果训练得出的支持向量个数比较少，那么SVM 训练出的模型比较容易被泛化。
• 由于满⾜KKT条件，⽀持向量机的优化问题通常可以转换为对偶问题求解。
• 通过引入松弛变量，我们可以训练得到软约束的⽀持向量机。
• 可以通过使用核函数让⽀持向量机处理线性不可分数据。