pytorch深度学习实战lesson18

第十八课 卷积层

卷积是深度学习最重要的概念之一，下面来学习和回顾一下卷积的基本概念。

目录

理论部分

从全连接层到卷积层

卷积层

实践部分

---

理论部分

从全连接层到卷积层

还是从一个例子开始：假设我要对猫和狗进行分类。

假设我用一千二百万像素的手机拍照，排成的图片是RGB图片（有3个通道），RGB图像有三千六百万个元素。假设用隐藏层大小为100的mlp进行训练的话，这个模型就要有36亿个参数，远远多于世界上猫狗的总量了，还不如记住世界上所有的猫狗来的划算。

所以使用mlp处理比较大的图片的时候必须要考虑和解决这个问题。

下面回顾一下单隐藏层的mlp。

如上图所示，我输入有三千六百万个时，当输入到有100个隐藏层神经元的神经网络时，需要有三千六百万乘100个权重，也就是36亿个元素，这大概需要14个G去存权重，这仅仅是单层神经网络存权重所需要的空间，那么对于多层来讲那就爆炸了，这是很荒谬的。

下面玩一个游戏：在人群中寻找图片左边的“Waldo”同志。

​

找的过程中需要遵循两个原则：

1、平移不变性

平移不变性是指，对于同一个图片分类器，无论被识别对象出现在图片的哪个位置，都能准确是识别出来。也就是说识别器不会因图片出现的位置而发生改变。

2、局部性

图片搜索的范围不用太大，区域够用即可。

全连接层到卷积层在数学层面的变化:

卷积的操作如上图所示。

也就是说，在w_{i,j,k,l}中，i,j代表输出的点在输出矩阵中的位置，k,l代表输入点在输入的图（或者矩阵）中的位置。那么这个权重矩阵应该记录输入中的每一个点对于输出中的每一个点的影响（也就是权重）。举例来说，比如输入图是4x4的，输出图是2x2的。我需要记录输入图中(1,1), (1,2), ..., (2,1), ..., (4,4)这些所有的点对输出图(1,1)的影响，同理也需要记录这些所有点对输出图中(1,2), ...., (2,2)的影响。那么这时候对于每一组点就有4个参数：输入图的横坐标、纵坐标，输出图的横坐标、纵坐标。所以要想完全记录所有的权重，所以需要一个4维张量。

下面看一下如何运用第一个原则——平移不变性。

这里要求无论i,j如何变换，v都不该变化，也就是说进行卷积计算时，所乘的权重矩阵，也就是卷积核，与位置(i, j)无关

原则二的意思就是说：研究输出hij时，我的卷积核不要太大，就只关注xij附近的元素即可。

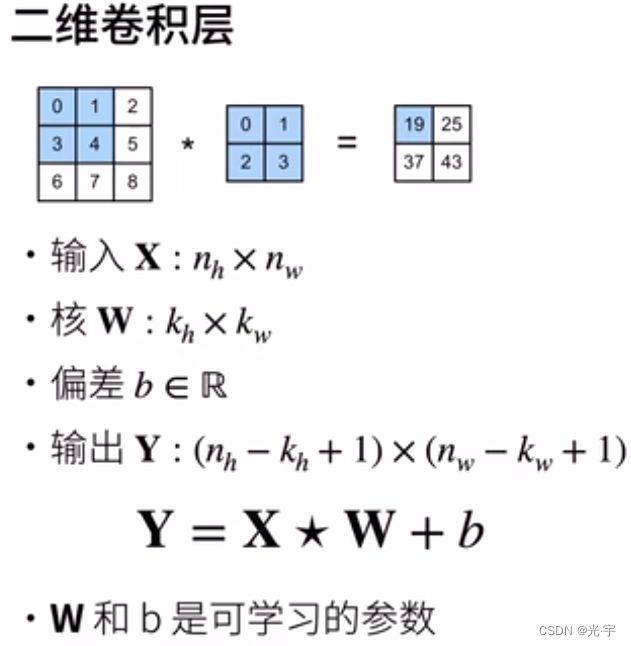
卷积层

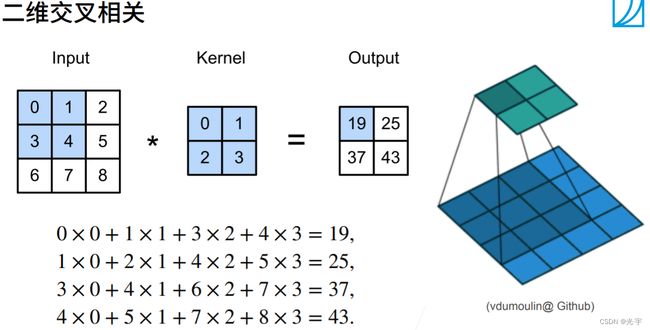
卷积的具体计算过程如上图所示。它的输出矩阵我们可以看到是卷积核与对应的输入阵进行按元素乘法和的结果。每算完一个卷积核的元素，卷积核就相对输入矩阵往右移一个，右移完了就往下移并且移到最左边，再开始计算。

关于卷积的例子：

不同的卷积核可以带来不同的效果。神经网络可以去学出来这些核去达到我们想要的图像效果。

这里给出的是二维交叉相关和二维卷积的区别，神经网络中的卷积层其实应用的是二维交叉相关这个公式。我们可以看到，它俩的区别从几何方面讲就是上下左右翻转的关系，所以卷积层和实际的数学领域的二维卷积是有一定区别的。

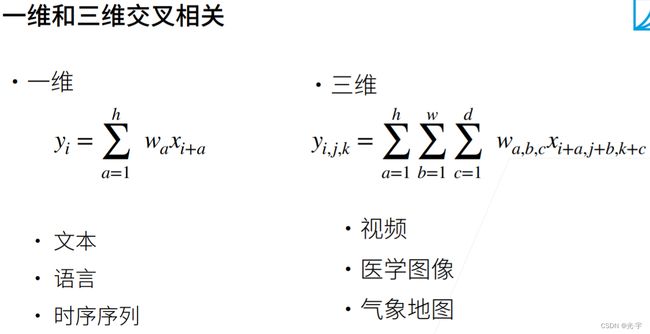
一维交叉相关的话，权重是个向量，一维交叉相关更适合处理一维的数据，比如文本、语言等；三维交叉相关参数也跟着变成了三维，它更适合处理视频、医学图像这种三维数据；二维交叉相关参数是二维的，它适合处理图像。它们之间的思想都大同小异。

卷积层相比全连接层的优点主要体现在参数计算量更小。

  全连接层每一个节点都要与下一层的每一个节点全部连接，每一个连接都有参数参与运算；而卷积层参数只与卷积核大小以及输出特征图的通道数相关。

  卷积层通过权值共享和稀疏连接来保证单层卷积中训练参数少。

实践部分

代码：

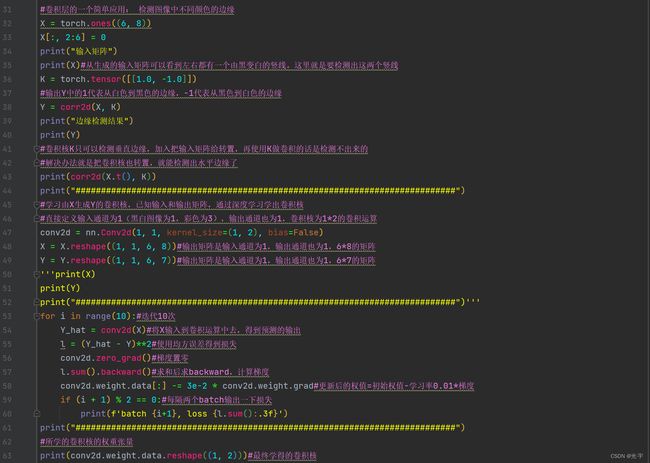
#图像卷积
#互相关运算
import torch
from torch import nn
from d2l import torch as d2l
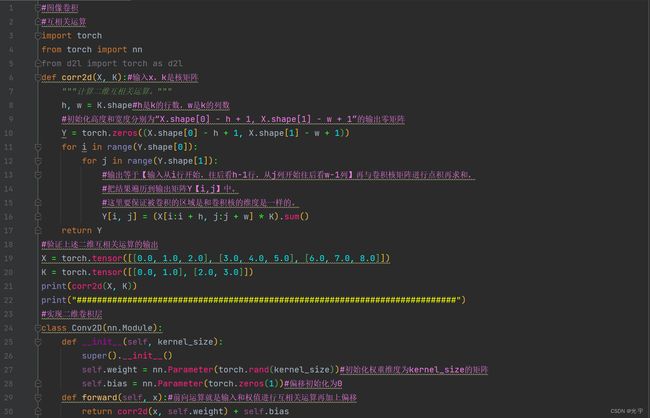
def corr2d(X, K):#输入x，k是核矩阵。二维交叉相关运算。
    """计算二维互相关运算。"""
    h, w = K.shape#h是卷积核的行数，w是卷积核的列数
    #初始化高度和宽度分别为“X.shape[0] - h + 1, X.shape[1] - w + 1”的输出零矩阵
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            #输出等于【输入从i行开始，往后看h-1行，从j列开始往后看w-1列】再与卷积核矩阵进行点积再求和，
            #把结果遍历到输出矩阵Y【i,j】中。
            #这里要保证被卷积的区域是和卷积核的维度是一样的。
            Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
    return Y
#验证上述二维交叉相关运算的输出
X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
print(corr2d(X, K))
print("###########################################################################")
#实现二维卷积层
class Conv2D(nn.Module):
    def __init__(self, kernel_size):
        super().__init__()
        self.weight = nn.Parameter(torch.rand(kernel_size))#初始化权重维度为kernel_size的矩阵
        self.bias = nn.Parameter(torch.zeros(1))#偏移初始化为0
    def forward(self, x):#前向运算就是输入和权值进行互相关运算再加上偏移
        return corr2d(x, self.weight) + self.bias
#卷积层的一个简单应用： 检测图像中不同颜色的边缘
X = torch.ones((6, 8))
X[:, 2:6] = 0
print("输入矩阵")
print(X)#从生成的输入矩阵可以看到左右都有一个由黑变白的竖线。这里就是要检测出这两个竖线
K = torch.tensor([[1.0, -1.0]])
#输出Y中的1代表从白色到黑色的边缘，-1代表从黑色到白色的边缘
Y = corr2d(X, K)
print("边缘检测结果")
print(Y)
#卷积核K只可以检测垂直边缘，加入把输入矩阵给转置，再使用K做卷积的话是检测不出来的
#解决办法就是把卷积核也转置，就能检测出水平边缘了
print(corr2d(X.t(), K))
print("###########################################################################")

#学习由X生成Y的卷积核，已知输入和输出矩阵，通过深度学习学出卷积核
#直接定义输入通道为1（黑白图像为1，彩色为3），输出通道也为1，卷积核为1*2的卷积运算
conv2d = nn.Conv2d(1, 1, kernel_size=(1, 2), bias=False)
X = X.reshape((1, 1, 6, 8))#输出矩阵是输入通道为1，输出通道也为1，6*8的矩阵
Y = Y.reshape((1, 1, 6, 7))#输出矩阵是输入通道为1，输出通道也为1，6*7的矩阵
'''print(X)
print(Y)
print("###########################################################################")'''
for i in range(10):#迭代10次
    Y_hat = conv2d(X)#将X输入到卷积运算中去，得到预测的输出
    l = (Y_hat - Y)**2#使用均方误差得到损失
    conv2d.zero_grad()#梯度置零
    l.sum().backward()#求和后求backward，计算梯度
    conv2d.weight.data[:] -= 3e-2 * conv2d.weight.grad#更新后的权值=初始权值-学习率0.01*梯度
    if (i + 1) % 2 == 0:#每隔两个batch输出一下损失
        print(f'batch {i+1}, loss {l.sum():.3f}')
print("###########################################################################")
#所学的卷积核的权重张量
print(conv2d.weight.data.reshape((1, 2)))#最终学得的卷积核

tensor([[19., 25.],
        [37., 43.]])
###########################################################################
输入矩阵
tensor([[1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.]])
边缘检测结果
tensor([[ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.]])
tensor([[0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.]])
###########################################################################
tensor([[[[1., 1., 0., 0., 0., 0., 1., 1.],
          [1., 1., 0., 0., 0., 0., 1., 1.],
          [1., 1., 0., 0., 0., 0., 1., 1.],
          [1., 1., 0., 0., 0., 0., 1., 1.],
          [1., 1., 0., 0., 0., 0., 1., 1.],
          [1., 1., 0., 0., 0., 0., 1., 1.]]]])
tensor([[[[ 0.,  1.,  0.,  0.,  0., -1.,  0.],
          [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
          [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
          [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
          [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
          [ 0.,  1.,  0.,  0.,  0., -1.,  0.]]]])
###########################################################################
batch 2, loss 8.089
batch 4, loss 2.323
batch 6, loss 0.785
batch 8, loss 0.294
batch 10, loss 0.116
###########################################################################
tensor([[ 1.0241, -0.9548]])