基于BOOTSTRAP方法的投资方案分析
【摘 要】
日常生活中存在各种各样的理财产品,本文以“华夏财富宝A”为例对常见经济现象进行数学建模并加以分析。实际情况下,基金收益情况受各种因素影响,但总体上遵循一定数学规律。本建模小组查阅相关资料后,决定选用Bootstrap方法对收益情况进行数学模拟。在实际操作过程中,我们先利用Excel表格分析得出收益情况正态分布函数。在较为理想的情况下,我们利用Bootstrap方法进行上万组数据的生成模拟,并通过VBA程序实现正态分布函数参数的计算。由于Bootstrap方法本身的科学性与我们数据量的庞大,计算结果较为科学,但为了保证模型的严谨性,我们将模拟数据与现实数据进行对照分析,以达到检验的目的。最终我们基本确定了数学模型的有效性。整个建模过程,核心算法采用经典统计学原理与国际知名方法,数据分析借助计算机软件完成,演算逻辑较为严谨。建立的模型可操作性强,符合问题要求。
关键词:
bootstrap方法 数学模型 VBA Excel 正态分布
1.前言
基金投资与理财是生活中非常重要的一部分,而我们常常会遇到关于不同投资决策的选择。但是由于财经往往受到社会各个方面因素的影响,我们就难以通过人为预测未来的收益变化来准确地选择最好的投资方案。为此,本建模小组试图利用建立数学模型的方法来作基于bootstrap方法的投资方案分析。
Bootstrap方法是Efron于1979年提出的一种逼近复杂统计量估计值分布的通用方法,在过去的30多年中,bootstrap方法被认为是统计学领域重要成果之一。[1]
2.问题重述
宁波银行推出一款理财产品“惠添利2099号”,98天,投资起点50000元,高于投资起点金额部分应为1000元份整数倍。年化收益率预计为5.2%,发售期为2018年2月1日至2018年3月14日,收益起始日期为3月15日,收益终止日期为6月21日,单利计算利息,理财产品中途若取出,则按银行活期利率计算利息。
华夏基金公司推出一款货币型基金“华夏财富宝A”,该基金的收益分配是按日结转份额的,每日收益支付方式采用红利再投资(即红利转基金份额)方式。该货币基金除去法定休息日外,随时可以申购和赎回,没有时间的限制。一般规定在交易日15:00前赎回,资金到账为2个交易日(T+2日)。
现假设手中恰有10万元,3月14日至6月21日期间想进行投资。
问题一:为了获得最大收益,投资人该进行怎样的投资策略;
问题二:若你想尽可能地保持资金的流动性(保证尽可能多的资金随时可用),那么10万块对两种产品如何配置,能使得获得的收益介于两者中最高收益95%与最小收益110%之间;
问题三:若假设你手上有a万块钱,且保证实时有b万元的流动资金,并考虑理财的风险(为规避风险可选择其它的理财方式,如存银行定期等);先建立适当的数学模型分析你的投资方案以供同学们投资参考。
3.问题分析
问题一:由题意可知为了获得最大收益,需比较宁波银行推出的理财产品“惠添利2099号”的年化收益率与华夏基金公司推出的货币金基金“华夏财富宝A”的七日年化收益率。通过查询能获得“华夏财富宝A”的基本的日每万份收益与七日年化收益率。我们通过比较得出较高者,而将手上的10万块全投入较高者即为投资人的投资策略,从而能获得最大收益。
问题二:我们可假设将x万元投入“惠添利2099号”,(10-x)万元投入“华夏财富宝A”。计算可得最高收益在将资金全投于“惠添利2099号”时取得,设其为w1;最小收益为将资金全投于“华夏财富宝A”,设其为w2.由题意可知收益w需介于0.95w1与1.10w2之间,且w=【x*5.2%+(10-x)*最新的七日年化收益率】*98/365,因此可以列出方程求得x的最小值,此时即保证尽量多的资金可随时使用。
问题三:宁波银行对年化收益率的预计具有相当的可靠性,故我们直接取用,而“华夏财富宝A”的基金收益每天都在改变,它的总体分布永远是未知的。但我们可以获取一个来自总体分布的数据样本,再应用bootstrap方法,得到bootstrap样本后对总体分布进行统计推断,以针对现在我们对总体分布知之甚少的情况。
为此我们会先建立收益分布的概率函数模型,再用bootstrap方法求得所需函数的参数,实现模型的求解。之后用该模型模拟未来的收益分布。最后通过模拟的收益分布计算回报,进行投资方案的分析。但是现实生活中存在投资风险,即未来投资收益具有不确定性,其影响因素大致可分为信用风险a、政策风险 b、利率风险 c、流动性风险 d、延期风险 e、提前终止风险 f、信息传递风险 g、其它风险h,因此收益总体分布F可用函数F(a,b,c,d,e,f,g,h)表示。在事实上,该函数的复杂性导致我们无法用运算形式给出表达式。[2]而我们所建立的模型将帮助我们对F的一个子样本进行推断。
4.问题解答
问题一:
解:
⑴资金全投于“惠添利2099号”,收益w1=100000*5.2%*98/365
=1396.16(元) (4.1.1)
⑵资金全投于“华夏财富宝A”,取其3月16日的7日年化收益率4.6580%,
可得收益w2=100000*4.6580%*98/365
=1250.64(元) (4.1.2)
由于w1>w2,可知将资金全投于“惠添利2099号”,可获得最大收益w=1396.16(元)。
问题二:
解:
由题最大收益的95%
w(2)=w1*95%=1326.36(元) (4.2.1)
最小收益的110%
w(2)=w2*110%=1375.71(元) (4.2.2)
可知收益
1326.36≤W≤1375.71 (4.2.3)
设x万元投于“惠添利2099号”,(10-x)万元投于“华夏财富宝A”
W=【x*5.2%+(10-x)*4.6580%】*98/365 (4.2.4)
联立(4.2.3)与(4.2.4)解得x的范围
5.201≤x≤8.598 (4.2.5)
根据题意保证尽可能多的流动资金,同时投入“惠添利2099号”的资金需高
于5万元且高出部分为1000元的整数倍,即取x的最小值x(min)=5.3(万
元)。即资金配置方案如下:投入资金5.3万元于“惠添利2099号”,投入
资金4.7万元于“华夏财富宝A”。
问题三:
根据问题三中的要求我们将进行数学模型的建立。
5.模型的建立及求解
5.1.建立正态分布函数模型
根据样本观测值,通过使用excel等软件绘制频率直方图的方法可以判断日每万份基金净收益的频率密度曲线大致为正态分布曲线,利用历史九个月日每万份基金净收益的数据,图像如图5.1所示。
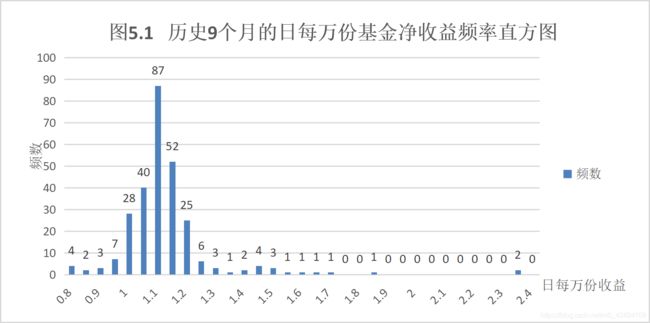
通过观察图5.1,我们发现收益的频率密度分布大致呈现正态分布。所以我们试图建立一个正态分布函数模型来得到日每万份基金净收益的概率密度。自变量X为日每万份基金净收益的值,因变量等于收益的概率密度。
f ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 f(x)=\frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}} f(x)=2πσ1e−2σ2(x−μ)2(5.1.1)
E ( X ) = ∫ − ∞ + ∞ x f ( x ) d x = ∫ − ∞ + ∞ x ⋅ 1 2 π σ e − ( x − μ ) 2 2 σ 2 d x E(X)=\int_{-\infty}^{+\infty} x f(x) d x=\int_{-\infty}^{+\infty} x \cdot \frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}} d x E(X)=∫−∞+∞xf(x)dx=∫−∞+∞x⋅2πσ1e−2σ2(x−μ)2dx(5.1.2)
D ( X ) = ∫ − ∞ + ∞ ( x − μ ) 2 f ( x ) d x = μ 2 π ∫ − ∞ + ∞ e − t 2 2 d t = μ D(X)=\int_{-\infty}^{+\infty}(x-\mu)^{2} f(x) d x=\frac{\mu}{\sqrt{2 \pi}} \int_{-\infty}^{+\infty} e^{-\frac{t^{2}}{2}} d t=\mu D(X)=∫−∞+∞(x−μ)2f(x)dx=2πμ∫−∞+∞e−2t2dt=μ(5.1.3)
令 x − μ σ = t , 令 \frac{x-\mu}{\sigma}=t, 令σx−μ=t, E ( X ) = 1 2 π ∫ − ∞ + ∞ ( σ t + μ ) e − t 2 2 d t E(X)=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{+\infty}(\sigma t+\mu) e^{-\frac{t^{2}}{2}} d t E(X)=2π1∫−∞+∞(σt+μ)e−2t2dt = 1 2 π σ ∫ − ∞ + ∞ ( x − μ ) 2 e − ( x − μ ) 2 2 σ 2 d x =\frac{1}{\sqrt{2 \pi} \sigma} \int_{-\infty}^{+\infty}(x-\mu)^{2} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}} d x =2πσ1∫−∞+∞(x−μ)2e−2σ2(x−μ)2dx(5.1.4)
D ( X ) = σ 2 2 π ∫ − ∞ + ∞ t 2 e − t 2 2 d t D(X)=\frac{\sigma^{2}}{\sqrt{2 \pi}} \int_{-\infty}^{+\infty} t^{2} e^{-\frac{t^{2}}{2}} d t D(X)=2πσ2∫−∞+∞t2e−2t2dt = σ 2 2 π ( [ − t e − t 2 2 ] − ∞ + ∞ + ∫ − ∞ + ∞ e − t 2 2 d t ) =\frac{\sigma^{2}}{\sqrt{2 \pi}}\left(\left[-t e^{-\frac{t^{2}}{2}}\right]_{-\infty}^{+\infty}+\int_{-\infty}^{+\infty} e^{-\frac{t^{2}}{2}} d t\right) =2πσ2([−te−2t2]−∞+∞+∫−∞+∞e−2t2dt) = 0 + σ 2 2 π 2 π = σ 2 =0+\frac{\sigma^{2}}{\sqrt{2 \pi}} \sqrt{2 \pi}=\sigma^{2} =0+2πσ22π=σ2(5.1.5)
也就是说,这个正态分布的概率密度中的两个参数μ和σ分别就是该分布的数学期望和标准差。我们可以通过它的数学期望和标准差来确定这个正态分布。[3]
模型假设如下:
(1)假设经济发展稳定,未发生严重的社会动荡。
(2)中途未出现因资金急用而导致的资金赎回。
(3)收益的频率分布呈正态分布。
下面我们将使用参数bootstrap方法来得到估计样本F(X)的数学期望。
5.2.由bootstrap方法求正态分布函数参数
对于总体分布F未知,但已经有一个容量为n的来自分布F的数学样本,自这一样本按放回抽样的方法抽取一个容量为n的样本,这种样本称
为bootstrap样本或称为自助样本。相继地、独立地自原始样本中取很多个bootstrap样本,利用这些样本对总体F进行统计推断。这种方法称为非参数bootstrap方法,又称自助法。现在由我们所建立的正态分布函数模型,得到了总体分布函数F的形式,其中包含未知参数μ与σ。再利用bootstrap样本对总体分布函数F的参数μ与σ进行统计推算。
我们所用的bootstrap估计的步骤如下:
1°自原始数据样本(“华夏财富宝A”历史 274天的日每万份基金净收益) x = ( x 1 , x 2 , . . . , x 274 ) x = (x_{1},x_{2},...,x_{274}) x=(x1,x2,...,x274)
按放回抽样的方法,抽得容量为n的样本
x ∗ = ( x 1 ∗ , x 2 ∗ , . . . , x 274 ∗ ) x^{*} = (x^{*}_{1},x^{*}_{2},...,x^{*}_{274}) x∗=(x1∗,x2∗,...,x274∗)(称为bootstrap样本)。
2°相继地独立地求出10000个样本容量为n的bootstrap样本, x ∗ 1 = ( x ∗ 1 , x ∗ 2 , . . . , x ∗ 274 ) x^{*_{1}}=(x^{*_{1}},x^{*_{2}},...,x^{*_{274}}) x∗1=(x∗1,x∗2,...,x∗274), i = 1,2,…,10000,
对于第i个bootstrap样本,计算 θ ^ i ∗ = θ ^ ( x 1 ∗ i , x 2 ∗ i , . . . , x 274 ∗ i ) \hat{\theta}^{*}_{i} = \hat{\theta}(x^{*_{i}}_{1},x^{*_{i}}_{2},...,x^{*_{i}}_{274}) θ^i∗=θ^(x1∗i,x2∗i,...,x274∗i), i = 1,2,…,10000, (称为θ的第i个bootstrap估计)。
3°计算各数值
上述步骤我们已通过附加“宏”的Excel文件实现。其中我们所求的θ代表中位数或20%截尾均值。(运算程序(宏1)见附件)
得到的结果如图5.2所示。
 对A列数据做计算,算出10000个bootstrap样本的中位数 M i ∗ ( i = 1 , 2 , . . . , 10000 ) M^{*}_{i}(i = 1,2,...,10000) Mi∗(i=1,2,...,10000)的均值 M ∗ ˉ = 1 10000 ∑ i = 1 10000 M i ∗ = 1.1302 , \bar{M^{*}} = \frac{1}{10000}\sum^{10000}_{i =1}{M^{*}_{i}} = 1.1302, M∗ˉ=100001i=1∑10000Mi∗=1.1302,
对A列数据做计算,算出10000个bootstrap样本的中位数 M i ∗ ( i = 1 , 2 , . . . , 10000 ) M^{*}_{i}(i = 1,2,...,10000) Mi∗(i=1,2,...,10000)的均值 M ∗ ˉ = 1 10000 ∑ i = 1 10000 M i ∗ = 1.1302 , \bar{M^{*}} = \frac{1}{10000}\sum^{10000}_{i =1}{M^{*}_{i}} = 1.1302, M∗ˉ=100001i=1∑10000Mi∗=1.1302,
将它放入单元格E2。计算各中位数与1.1302之差的平方和,除以9999,得0.0000252,放入单元格E4。计算0.0000252的平方根得0.005022,放入单元格E6,即我们所取用的参数σ,于是E6中的数是 σ ^ θ ^ = 1 9999 ∑ i = 1 10000 ( θ ^ i ∗ − θ ∗ ˉ ) 2 , \hat{\sigma}_{\hat{\theta}} = \sqrt{\frac{1}{9999}\sum^{10000}_{i = 1}{(\hat{\theta}^{*}_{i}-\bar{\theta^{*}})^2}}, σ^θ^=99991i=1∑10000(θ^i∗−θ∗ˉ)2,其中 θ ∗ ˉ = 1 10000 ∑ i = 1 10000 θ ^ i ∗ , \bar{\theta^{*}} = \frac{1}{10000}\sum^{10000}_{i =1}{\hat{\theta}^{*}_{i}}, θ∗ˉ=100001i=1∑10000θ^i∗,也就是我们要求的以样本中位数作为总体中位数的估计的标准误差的bootstrap估计。再计算1.1302与1.13155之差得0.00133,将它放入单元格E8,得偏差的bootstrap估计。计算各中位数与1.13155之差的平方的均值,得0.000027,放入单元格E10,于是E10中即为均方误差的bootstrap估计。
运算结果如Excel表格中显示,将A列数据(由bootstrap样本求出的中位数)升序排序后,并将C列数据(由bootstrap样本求出的截尾均值)。如表5.2.1与表5.2.2所示。
可以读出下列数据: 从而得:
从而得:
 为 了 考 虑 投 资 理 财 的 保 守 性 及 风 险 的 复 杂 性 , 我 们 在 得 到 了 中 位 数 和 截 尾 均 值 的 置 信 区 间 为了考虑投资理财的保守性及风险的复杂性,我们在得到了中位数和截尾均值的置信区间 为了考虑投资理财的保守性及风险的复杂性,我们在得到了中位数和截尾均值的置信区间 后 将 选 择 中 位 数 在 置 信 水 平 α = 0.95 时 的 单 侧 置 信 上 限 θ ˉ 作 为 正 态 分 布 函 数 f ( x ) 的 参 数 μ ( 均 值 ) ; 后将选择中位数在置信水平α=0.95时的单侧置信上限\bar{\theta}作为正态分布函数f(x)的参数μ(均值); 后将选择中位数在置信水平α=0.95时的单侧置信上限θˉ作为正态分布函数f(x)的参数μ(均值); 再 选 择 以 样 本 中 位 数 作 为 总 体 中 位 数 的 估 计 的 标 准 误 差 的 b o o t s t r a p 估 计 σ ^ θ ^ 作 为 参 数 σ ( 均 方 差 ) 。 再选择以样本中位数作为总体中位数的估计的标准误差的bootstrap估计\hat{\sigma}_{\hat{\theta}}作为参数σ(均方差)。 再选择以样本中位数作为总体中位数的估计的标准误差的bootstrap估计σ^θ^作为参数σ(均方差)。
为 了 考 虑 投 资 理 财 的 保 守 性 及 风 险 的 复 杂 性 , 我 们 在 得 到 了 中 位 数 和 截 尾 均 值 的 置 信 区 间 为了考虑投资理财的保守性及风险的复杂性,我们在得到了中位数和截尾均值的置信区间 为了考虑投资理财的保守性及风险的复杂性,我们在得到了中位数和截尾均值的置信区间 后 将 选 择 中 位 数 在 置 信 水 平 α = 0.95 时 的 单 侧 置 信 上 限 θ ˉ 作 为 正 态 分 布 函 数 f ( x ) 的 参 数 μ ( 均 值 ) ; 后将选择中位数在置信水平α=0.95时的单侧置信上限\bar{\theta}作为正态分布函数f(x)的参数μ(均值); 后将选择中位数在置信水平α=0.95时的单侧置信上限θˉ作为正态分布函数f(x)的参数μ(均值); 再 选 择 以 样 本 中 位 数 作 为 总 体 中 位 数 的 估 计 的 标 准 误 差 的 b o o t s t r a p 估 计 σ ^ θ ^ 作 为 参 数 σ ( 均 方 差 ) 。 再选择以样本中位数作为总体中位数的估计的标准误差的bootstrap估计\hat{\sigma}_{\hat{\theta}}作为参数σ(均方差)。 再选择以样本中位数作为总体中位数的估计的标准误差的bootstrap估计σ^θ^作为参数σ(均方差)。
将参数代入(1,1)式中的概率密度得到估计的正态分布模型。
f ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 , f(x)=\frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}} , f(x)=2πσ1e−2σ2(x−μ)2,μ=1.1386,σ=0.005021958718 (5.2)
5.3.由正态分布函数模拟未来收益变化
因为基金公司所给数据保留四位小数,故我们的模拟数据同样给出四位小数,即最小为为0.0001。之后将区间[μ-3σ,μ+3σ](根据“3σ”法则)中的数据进行量化,得到每个量化数的概率值。所得区间为[1.1235,1.1537],量化间隔(STEP)为0.0001。
再通过“密铺”的方法,即将以每个量化数的概率值为长度的小线段衔接起来组成一个长线段,在该线段上用随机函数随机选取一个点,将该点所在小线段对应的量化值作为随机所取的当日每份基金收益。(运算(宏2)见附件)
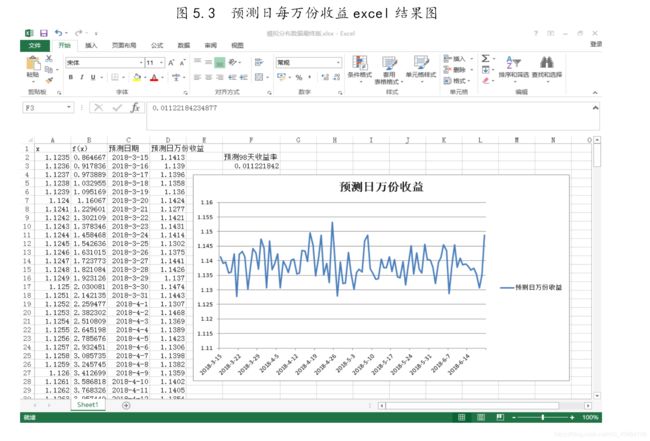
所以模拟出未来(2018年3月15日至2018年6月21日)98天的基金收益变化变化曲线结果如图5.3所示。
5.4.根据模拟未来收益计算 “华夏财富宝A”在98日后的回报
由 表 格 中 的 数 据 , 令 第 i 日 的 日 每 万 份 基 金 净 收 益 为 a i 。 由表格中的数据,令第i日的日每万份基金净收益为a_{i}。 由表格中的数据,令第i日的日每万份基金净收益为ai。
回报 w = x [ ∏ i = 1 98 ( a i + 1 ) − 1 ] = 0.011221842 x w = x[\prod^{98}_{i =1}{(a_{i}+1)}-1] = 0.011221842 x w=x[i=1∏98(ai+1)−1]=0.011221842x(5.4)
5.5.投资方案分析
y是购买宁波银行“惠添利2099号”的金额且y应为1000整数倍。
总回报 W = y 98 365 5.20 % + w , x ≥ b W = y\frac{98}{365}5.20%+w,x≥b W=y365985.20%+w,x≥b (5.5)
根据数学分析可知x取b时有总回报W最高,并且该总回报的预期为(0.013962y+0.011221842b)元。
5.6.带入数据
代入一组假设数据a=10,b=2.5 ,且投资者属于稳健型投资者。对于稳健型投资者,其应当具备承担中风险的能力。[4]
根据分析,b=2.5,y=7.5,由公式(5.4.2)得到W=1327.70与问题二中所计算得到的公式(4.2.1)与(4.2.2)相比较,发现W落在区间(4.2.3)中,所以得到的投资回报处于投资者的接受范围内,该投资方案经分析后可知合理。[5]
6.模型的检验
取2017年3月8日至2017年12月6日的274个的日每万份收益数据,使用所建立的数学模型,即用bootstrap方法估计参数后,将参数带入正态分布函数,得到2017年12月7日至2018年3月14日的日每万份收益率预测数据,据此得到此98天的预测收益1096.77元,与实际收益1202.34元比较少了105.57元。该结果在我们的预算之中。根据查阅的资料,对应时期的实际收益偏高的原因或许与通货膨胀有关。如图6所示。
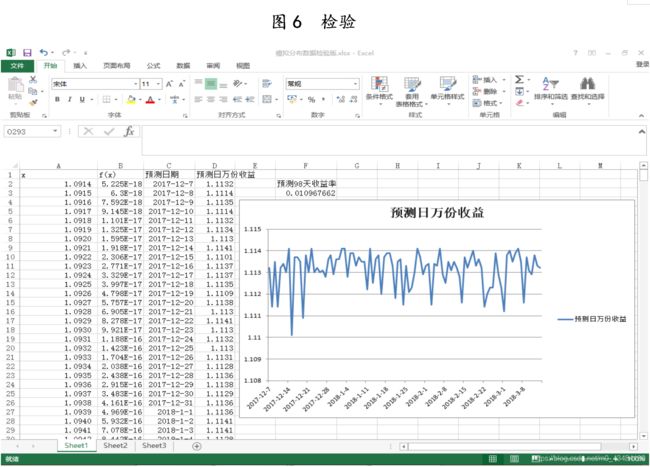
7.模型的评价
7.1模型的优点
1.通过对应网站和资源找出的相关数据和公式,计算结果相对准确。
2.用bootstrap方法估计参数,bootstrap是现代统计学较为流行的一种统计方法,在小样本时效果很好。通过方差的估计可以构造置信区间等,其运用范围得到进一步延伸。
3.有关模型的计算采用了对应的数学软件,结果准确。
4.提出了合理的假设并对模型所设计的影响因素进行了量化分析,使论文更有说服力。
5.该模型是建模队伍自己的智慧成果,原创性较高。
6.运用了Excel、VBA等计算机软件可以有效对问题作出较准确的处理并用不同的图表使结果直观清晰。
7.2模型的缺点和不足
1.可能因考虑因素的不全面,导致模型不准确。[6]
2.参考数据的量较少,难以具备较强的说服力。
3.若将模型运用到实际,则需要根据实际情况来增添不同的变量,导致模型精度发生变化,计算难度加大。
8.结束语
本文基于bootstrap方法研究“华夏财富宝A”的预期收益情况,做出投资风险分析,主要工作在于利用VBA、Excel数据分析实现bootstrap方法,对往期收益数据进行统计分析,模拟生成收益。利用计算机随机数程序来模拟现实基金的不确定性,同时加入“密铺”等算法控制基金波动。检验过程主要是利用本文介绍的算法所生成的模拟收益与现存往年同期数据比对,进行误差分析,验证得出本算法可操作性与模拟收益情况都在可接受范围内,并与心理预期较为吻合。本次研究的意义在于利用数学建模对日常经济现象进行分析、模拟,借助高中生能力范围之内的工具进行科学、直观的操作,较为符合学校“数学节”的开展理念,能够锻炼学生的综合数学思维能力与实际应用能力。同时,我们的算法为投资风险分析提供了一种较为简单科学的研究方法,使模型与实际较接近,具有一定价值。
参考文献
[1] 徐王茗 邓超 吴军.《基于bootstrap方法的可靠性评估》. 机械设计与制造. 2009-05-29
[2] N. 格里高利·曼昆 .《经济学原理》. 机械工业出版社. 2002-09-01
[3] 陈爱江 张文良 .《概率论与数理统计》.中国质检出版社.2011-06-01
[4] 朱平辉 .《投资风险管理》. 厦门大学出版社. 2007年
[5] 马严彬. 《项目可行性报告范文》. 蓝天出版社. 2011年
[6] 杨启帆 .《数学建模》. 高等教育出版社. 2005-05-01
附件:
(宏1)
Private Sub Worksheet_BeforeDoubleClick(ByVal Target As Range, Cancel As Boolean)
Dim i As Integer, j As Integer, m As Integer, n As Integer, k As Integer, t As Double, p As Double
Dim yn As Integer, r As Integer
Dim a(1 To 10000) As Double
Dim b(1 To 1000) As Double
Dim sum, e2, e4, e8, e10, zws As Double
n = 274
For i = 2 To 10001
p = 0
For j = 9 To n + 8
m = Int(Rnd * n + 1)
Sheet1.Cells(i, j) = Sheet1.Cells(m + 1, 7) '产生随机样本
t = Sheet1.Cells(m + 1, 7)
For k = j - 1 To 9 Step -1
If a(k) > t Then
a(k + 1) = a(k)
Else
Exit For
End If
Next k '样本内部排序
a(k + 1) = t
p = p + t
Next j
t = (a((n + 1) \ 2 + 8) + a(n \ 2 + 9)) / 2
Sheet1.Cells(i, 1) = t '输出中位数至A列
For j = 1 To Int(n * 0.1)
p = p - a(j + 8) - a(n + 9 - j)
Next j
p = p / (n - 2 * Int(n * 0.1))
Sheet1.Cells(i, 3) = p '输出20%截尾平均数
Next i
yn = 10000 '样本数据容量
n = 274 '历史数据容量
e2 = 0
For i = 1 To yn
a(i) = Sheet1.Cells(i + 1, 1)
e2 = e2 + a(i)
Next i
e2 = e2 / yn '样本中位数均值
Sheet1.Cells(2, 5) = e2
sum = 0
For i = 1 To yn
sum = sum + (e2 - a(i)) ^ 2
Next i
e4 = sum / 9999 '样本中位数方差
e6 = Sqr(e4) '标准误差
Sheet1.Cells(4, 5) = e4
End Sub
(宏2)
Private Sub Worksheet_BeforeDoubleClick(ByVal Target As Range, Cancel As Boolean)
Dim i As Integer, n As Integer, j As Integer, r As Double, a(1 To 16000) As Double, b(1 To 16000) As Double, l(0 To 16000) As Double, future(1 To 98) As Double
n = 303
l(0) = 0
For i = 1 To n
a(i) = Sheet1.Cells(i + 1, 1)
b(i) = Sheet1.Cells(i + 1, 2)
l(i) = b(i) + l(i - 1)
Next i
For j = 1 To 98
r = Rnd() * l(n)
For i = 1 To n
If r < l(i) Then
future(j) = a(i)
Exit For
End If
Next i
Next j
For j = 1 To 98
Sheet1.Cells(j + 1, 4) = future(j)
Next j
End Sub
Private Sub Worksheet_SelectionChange(ByVal Target As Range)
dim i,j,k,m,n as long
dim p,e,u,s as double
dim a(1 to 1000)as double
dim b(1 to 1000)as double
n=303
p=3.14159265358979
e=2.71828182845905
s=0.005021958718 's=σ
u=1.1386 'u=μ
for i = 1 to n
a(i)=sheet1.cells(i+1,1)
b(i)=1/(sqr(2*p)*s)*e^(-(a(i)-u)^2/(2*s^2))
sheet1.cells(i+1,2)=b(i)
next i
End Sub