SLAM14讲-ch12建图笔记

1. 单目稠密重建

遇到了一个问题，google解决了：运行ch12 单目稠密建图的程序时出现段错误（核心已转储）
不得不感叹Google比百度好用太多了。另外，在高博的Github下面有很多关于书上例程bug的讨论，遇到问题可以到这里看看。

gdb好像挺有用，挖个坑，有空来填。

1.1 单目稠密重建代码注释

针对教材中的单目稠密重建，代码量有些大，而且有些复杂，这里做简要介绍。
首先对整个单目稠密重建流程进行梳理：

1. 任务使用200张图片对第1张图片上每个像素的深度值进行估计，即进行单目稠密重建。
2. 读取第1张图片作为ref，后面的图片是cur，我们的任务就是对第一张图片中的深度的均值和方差进行估计更新；
3. 遍历ref中所有像素，分别在各个cur中进行极线搜索和块匹配（因为这里是对所有像素点而不是特征点进行匹配，所以没有之前前端1中的特征点的描述子，此处需要确定极线位置，即极线搜索，使用深度均值的初始值来计算初始的极线位置，再不断优化深度的均值和方差；确定极线位置之后使用块匹配，此处使用3*3的窗口，计算窗口内坐标ref和cur内的像素的NCC，若NCC高于阈值，则认为匹配成功，否则匹配失败。取NCC最大的作为此次的块匹配结果，若匹配成功则将cur中对应的点作为ref中对应点的匹配）
4. 根据三角化计算深度（均值）和不确定性（方差）。（难点，此处为手写而非调库，注释中有详细讲解）
5. 将当前观测融合进上次估计中，并检查是否收敛（我们的目的是通过我们对cur的观测来不断优化之前的估计$\mu ,\sigma$，对应到程序里的depth和depth_cov2各个坐标的值，先取出，再融合，实现更新的目的。）

简单的图示：

#include 
#include 
#include 

using namespace std;

#include 

// for sophus
#include 

using Sophus::SE3d;

// for eigen
#include 
#include 

using namespace Eigen;

#include 
#include 
#include 

using namespace cv;

/**********************************************
* 本程序演示了单目相机在已知轨迹下的稠密深度估计
* 使用极线搜索 + NCC 匹配的方式，与书本的 12.2 节对应
* 请注意本程序并不完美，你完全可以改进它——我其实在故意暴露一些问题(这是借口)。
***********************************************/

// ------------------------------------------------------------------
// parameters
const int boarder = 20;         // 边缘宽度
const int width = 640;          // 图像宽度
const int height = 480;         // 图像高度
const double fx = 481.2f;       // 相机内参
const double fy = -480.0f;
const double cx = 319.5f;
const double cy = 239.5f;
const int ncc_window_size = 3;    // NCC 取的窗口半宽度
const int ncc_area = (2 * ncc_window_size + 1) * (2 * ncc_window_size + 1); // NCC窗口面积
const double min_cov = 0.1;     // 收敛判定：最小方差
const double max_cov = 10;      // 发散判定：最大方差

// ------------------------------------------------------------------
// 重要的函数
/// 从 REMODE 数据集读取数据
bool readDatasetFiles(
    const string &path,
    vector<string> &color_image_files,
    vector<SE3d> &poses,
    cv::Mat &ref_depth
);

/**
 * 根据新的图像更新深度估计
 * @param ref           参考图像
 * @param curr          当前图像
 * @param T_C_R         参考图像到当前图像的位姿
 * @param depth         深度
 * @param depth_cov     深度方差
 * @return              是否成功
 */
void update(
    const Mat &ref,
    const Mat &curr,
    const SE3d &T_C_R,
    Mat &depth,
    Mat &depth_cov2
);

/**
 * 极线搜索
 * @param ref           参考图像
 * @param curr          当前图像
 * @param T_C_R         位姿
 * @param pt_ref        参考图像中点的位置
 * @param depth_mu      深度均值
 * @param depth_cov     深度方差
 * @param pt_curr       当前点
 * @param epipolar_direction  极线方向
 * @return              是否成功
 */
bool epipolarSearch(
    const Mat &ref,
    const Mat &curr,
    const SE3d &T_C_R,
    const Vector2d &pt_ref,
    const double &depth_mu,
    const double &depth_cov,
    Vector2d &pt_curr,
    Vector2d &epipolar_direction
);

/**
 * 更新深度滤波器
 * @param pt_ref    参考图像点
 * @param pt_curr   当前图像点
 * @param T_C_R     位姿
 * @param epipolar_direction 极线方向
 * @param depth     深度均值
 * @param depth_cov2    深度方向
 * @return          是否成功
 */
bool updateDepthFilter(
    const Vector2d &pt_ref,
    const Vector2d &pt_curr,
    const SE3d &T_C_R,
    const Vector2d &epipolar_direction,
    Mat &depth,
    Mat &depth_cov2
);

/**
 * 计算 NCC 评分
 * @param ref       参考图像
 * @param curr      当前图像
 * @param pt_ref    参考点
 * @param pt_curr   当前点
 * @return          NCC评分
 */
double NCC(const Mat &ref, const Mat &curr, const Vector2d &pt_ref, const Vector2d &pt_curr);

// 双线性灰度插值
inline double getBilinearInterpolatedValue(const Mat &img, const Vector2d &pt) {
    uchar *d = &img.data[int(pt(1, 0)) * img.step + int(pt(0, 0))];
    double xx = pt(0, 0) - floor(pt(0, 0));
    double yy = pt(1, 0) - floor(pt(1, 0));
    return ((1 - xx) * (1 - yy) * double(d[0]) +
            xx * (1 - yy) * double(d[1]) +
            (1 - xx) * yy * double(d[img.step]) +
            xx * yy * double(d[img.step + 1])) / 255.0;
}

// ------------------------------------------------------------------
// 一些小工具
// 显示估计的深度图
void plotDepth(const Mat &depth_truth, const Mat &depth_estimate);

// 像素到相机坐标系
inline Vector3d px2cam(const Vector2d px) {
    return Vector3d(
        (px(0, 0) - cx) / fx,
        (px(1, 0) - cy) / fy,
        1
    );
}

// 相机坐标系到像素
inline Vector2d cam2px(const Vector3d p_cam) {
    return Vector2d(
        p_cam(0, 0) * fx / p_cam(2, 0) + cx,
        p_cam(1, 0) * fy / p_cam(2, 0) + cy
    );
}

// 检测一个点是否在图像边框内
inline bool inside(const Vector2d &pt) {
    return pt(0, 0) >= boarder && pt(1, 0) >= boarder
           && pt(0, 0) + boarder < width && pt(1, 0) + boarder <= height;
}

// 显示极线匹配
void showEpipolarMatch(const Mat &ref, const Mat &curr, const Vector2d &px_ref, const Vector2d &px_curr);

// 显示极线
void showEpipolarLine(const Mat &ref, const Mat &curr, const Vector2d &px_ref, const Vector2d &px_min_curr,
                      const Vector2d &px_max_curr);

/// 评测深度估计
void evaludateDepth(const Mat &depth_truth, const Mat &depth_estimate);
// ------------------------------------------------------------------


int main(int argc, char **argv) {
    if (argc != 2) {
        cout << "Usage: dense_mapping path_to_test_dataset" << endl;
        return -1;
    }
    // 从数据集读取数据
    vector<string> color_image_files;
    vector<SE3d> poses_TWC;
    Mat ref_depth;
    //读取图片、相机位姿、深度参考值（用于计算深度重建的误差）
    bool ret = readDatasetFiles(argv[1], color_image_files, poses_TWC, ref_depth);
//    bool ret = readDatasetFiles("../remode_test_data/test_data/", color_image_files, poses_TWC, ref_depth);
    if (ret == false) {
        cout << "Reading image files failed!" << endl;
        return -1;
    }
    cout << "read total " << color_image_files.size() << " files." << endl;

    // 第一张图ref
    Mat ref = imread(color_image_files[0], 0);                // gray-scale image
    SE3d pose_ref_TWC = poses_TWC[0];
    double init_depth = 3.0;    // 深度初始值
    double init_cov2 = 3.0;     // 方差初始值
    Mat depth(height, width, CV_64F, init_depth);             // 深度图
    Mat depth_cov2(height, width, CV_64F, init_cov2);         // 深度图方差

    // 从第一张图开始往后读所有的图cur
    for (int index = 1; index < color_image_files.size(); index++)
    {
        cout << "*** loop " << index << " ***" << endl;
        Mat curr = imread(color_image_files[index], 0);  //读图
        if (curr.data == nullptr) continue;
        SE3d pose_curr_TWC = poses_TWC[index];    //读出来的是TWC

        // 坐标转换关系： T_C_W * T_W_R = T_C_R  关于这里为什么是T_W_R，W是world世界系；R是Reference参考系，即第一帧的相机系
        // 根据同一个路标点的P_w相同，有T_WC * P_C = T_WR * P_R，
        // 两边同乘(T_WC)^(-1)即得P_C = (T_WC)^(-1) * T_WR * P_R = T_CR * P_R，从参考系转到当前系
        SE3d pose_T_C_R = pose_curr_TWC.inverse() * pose_ref_TWC;

        update(ref, curr, pose_T_C_R, depth, depth_cov2);  //对深度图进行更新
        evaludateDepth(ref_depth, depth);
        plotDepth(ref_depth, depth);
        imshow("image", curr);
        waitKey(1);
    }

    cout << "estimation returns, saving depth map ..." << endl;
    imwrite("depth.png", depth);
    cout << "done." << endl;

    return 0;
}

bool readDatasetFiles(
    const string &path,
    vector<string> &color_image_files,
    std::vector<SE3d> &poses,
    cv::Mat &ref_depth) {
    ifstream fin(path + "/first_200_frames_traj_over_table_input_sequence.txt");
    if (!fin) return false;

    while (!fin.eof())
    {
        // 数据格式：图像文件名 tx, ty, tz, qx, qy, qz, qw ，注意是 TWC 而非 TCW   是相机转到世界
        string image;
        fin >> image;
        double data[7];
        for (double &d:data) fin >> d;

        color_image_files.push_back(path + string("/images/") + image);
        poses.push_back(
            SE3d(Quaterniond(data[6], data[3], data[4], data[5]),   //构造四元数时实部在前
                 Vector3d(data[0], data[1], data[2]))
        );
        if (!fin.good()) break;
    }
    fin.close();

    // load reference depth  为什么要有参考depth？为了计算对于ref深度估计的误差。
    fin.open(path + "/depthmaps/scene_000.depth");
    ref_depth = cv::Mat(height, width, CV_64F);
    if (!fin) return false;
    for (int y = 0; y < height; y++)
        for (int x = 0; x < width; x++) {
            double depth = 0;
            fin >> depth;
            ref_depth.ptr<double>(y)[x] = depth / 100.0;
        }
    return true;
}

// 对整个深度图进行更新
void update(const Mat &ref, const Mat &curr, const SE3d &T_C_R, Mat &depth, Mat &depth_cov2) {
    for (int x = boarder; x < width - boarder; x++)
        for (int y = boarder; y < height - boarder; y++) {
            // 遍历每个像素
            // 检查是否收敛
            if (depth_cov2.ptr<double>(y)[x] < min_cov || depth_cov2.ptr<double>(y)[x] > max_cov) // 深度已收敛或发散
                continue;
            // 在极线上搜索 (x,y) 的匹配
            Vector2d pt_curr;
            Vector2d epipolar_direction;
            // 极线搜索最相似的块（以NCC作为评判标准）
            bool ret = epipolarSearch(
                ref,        //参考图像
                curr,       //当前图像
                T_C_R,      //位姿
                Vector2d(x, y),  //参考图像中点的位置
                depth.ptr<double>(y)[x],  //深度均值
                sqrt(depth_cov2.ptr<double>(y)[x]),  //深度方差
                pt_curr,    //当前点
                epipolar_direction  //极线方向
            );

            if (ret == false) // 匹配失败
                continue;

            // 取消该注释以显示匹配
            // showEpipolarMatch(ref, curr, Vector2d(x, y), pt_curr);

            // 匹配成功，（使用三角化）更新深度图
            updateDepthFilter(Vector2d(x, y), pt_curr, T_C_R, epipolar_direction, depth, depth_cov2);
        }
}

// 极线搜索和块匹配：
// 1.极线搜索：因为这里是对所有像素点而不是特征点进行匹配，所以没有之前前端1中的特征点的描述子，此处需要确定极线位置，即极线搜索，
// 使用深度均值的初始值来计算初始的极线位置，再不断优化深度的均值和方差；
// 2.块匹配：确定极线位置之后使用块匹配，此处使用3*3的窗口，计算窗口内坐标ref和cur内的像素的NCC，若NCC高于阈值，则认为匹配成功，否则匹配失败。
// 取NCC最大的作为此次的块匹配结果，若匹配成功则将cur中对应的点作为ref中对应点的匹配
// 方法见书 12.2 12.3 两节
bool epipolarSearch(
    const Mat &ref, const Mat &curr,
    const SE3d &T_C_R, const Vector2d &pt_ref,
    const double &depth_mu, const double &depth_cov,
    Vector2d &pt_curr, Vector2d &epipolar_direction)
    {
    Vector3d f_ref = px2cam(pt_ref);  // 参考点像素转为P_R uv1
    f_ref.normalize();
    Vector3d P_ref = f_ref * depth_mu;    // 参考帧的相机系坐标P_ref

    Vector2d px_mean_curr = cam2px(T_C_R * P_ref); // 按深度均值(高斯分布的均值)投影的像素（传入的是相机系坐标）
    double d_min = depth_mu - 3 * depth_cov, d_max = depth_mu + 3 * depth_cov;   //正负3倍的方差
    if (d_min < 0.1) d_min = 0.1;
    //分别按最大和最小深度投影获得极线线段的两端点
    Vector2d px_min_curr = cam2px(T_C_R * (f_ref * d_min));    // 按最小深度投影的像素
    Vector2d px_max_curr = cam2px(T_C_R * (f_ref * d_max));    // 按最大深度投影的像素

    Vector2d epipolar_line = px_max_curr - px_min_curr;    // 极线（线段形式）
    epipolar_direction = epipolar_line;        // 极线方向
    epipolar_direction.normalize();
    double half_length = 0.5 * epipolar_line.norm();    // 极线线段的半长度
    if (half_length > 100) half_length = 100;   // 我们不希望搜索太多东西

    // 取消此句注释以显示极线（线段）
    // showEpipolarLine( ref, curr, pt_ref, px_min_curr, px_max_curr);

    // 在极线上搜索，以深度均值点为中心，左右各取半长度
    double best_ncc = -1.0;
    Vector2d best_px_curr;
    for (double l = -half_length; l <= half_length; l += 0.7) { // l+=sqrt(2)
        Vector2d px_curr = px_mean_curr + l * epipolar_direction;  // 待匹配点
        if (!inside(px_curr))
            continue;
        // 计算待匹配点与参考帧的 NCC(去均值计算NCC，教材P322式(12.11))
        double ncc = NCC(ref, curr, pt_ref, px_curr);
        if (ncc > best_ncc) {
            best_ncc = ncc;
            best_px_curr = px_curr;
        }
    }
    if (best_ncc < 0.85f)      // 只相信 NCC 很高的匹配
        return false;
    pt_curr = best_px_curr;
    return true;
}

double NCC(
    const Mat &ref, const Mat &curr,
    const Vector2d &pt_ref, const Vector2d &pt_curr) {
    // 零均值-归一化互相关
    // 先算均值
    double mean_ref = 0, mean_curr = 0;
    vector<double> values_ref, values_curr; // 参考帧和当前帧的均值
    //块匹配这里取3*3的块
    for (int x = -ncc_window_size; x <= ncc_window_size; x++)
        for (int y = -ncc_window_size; y <= ncc_window_size; y++) {
            double value_ref = double(ref.ptr<uchar>(int(y + pt_ref(1, 0)))[int(x + pt_ref(0, 0))]) / 255.0;
            mean_ref += value_ref;

            double value_curr = getBilinearInterpolatedValue(curr, pt_curr + Vector2d(x, y));
            mean_curr += value_curr;

            values_ref.push_back(value_ref);
            values_curr.push_back(value_curr);
        }

    mean_ref /= ncc_area;
    mean_curr /= ncc_area;

    // 计算 Zero mean NCC  去均值计算NCC
    double numerator = 0, demoniator1 = 0, demoniator2 = 0;
    for (int i = 0; i < values_ref.size(); i++) {
        double n = (values_ref[i] - mean_ref) * (values_curr[i] - mean_curr);
        numerator += n;
        demoniator1 += (values_ref[i] - mean_ref) * (values_ref[i] - mean_ref);
        demoniator2 += (values_curr[i] - mean_curr) * (values_curr[i] - mean_curr);
    }
    return numerator / sqrt(demoniator1 * demoniator2 + 1e-10);   // 防止分母出现零
}

bool updateDepthFilter(
    const Vector2d &pt_ref,
    const Vector2d &pt_curr,
    const SE3d &T_C_R,
    const Vector2d &epipolar_direction,
    Mat &depth,
    Mat &depth_cov2) {
    // 不知道这段还有没有人看
    // 用三角化计算深度
    SE3d T_R_C = T_C_R.inverse();
    Vector3d f_ref = px2cam(pt_ref);
    f_ref.normalize();
    Vector3d f_curr = px2cam(pt_curr);
    f_curr.normalize();

    // 方程
    // d_ref * f_ref = d_cur * ( R_RC * f_cur ) + t_RC
    // f2 = R_RC * f_cur
    // 转化成下面这个矩阵方程组
    // => [ f_ref^T f_ref, -f_ref^T f2 ] [d_ref]   [f_ref^T t]
    //    [ f_2^T f_ref, -f2^T f2      ] [d_cur] = [f2^T t   ]
    // 二阶方程用克莱默法则求解并解之
    //克莱默法则是先算齐次行列式的值D，然后用常数项b依次替换掉i列，算行列式Di，Di/D即为xi的值
    Vector3d t = T_R_C.translation();
    Vector3d f2 = T_R_C.so3() * f_curr;


    //重点来了：令x1=f_ref, x2=f_cur R=R_RC t=t_RC
    //s1*x1=s2*R*x2+t,移项得到s1*x1-s2*R*x2=t   (1)
    //(1)两边同乘x1的转置x1T，得s1*x1T*x1-s2*x1T*R*x2=x1T*t   (2) 注意"T"指的是转置的意思
    //(1)两边同乘（R*x2）T，得s1*(R*x2)T*x1-s2*((R*x2)T)*R*x2=(R*x2)T * t (3)
    //因此接下来的A[]就是存放未知数为s1和s2的线性方程组的系数矩阵，b存放方程组右端的两个常数
    //此处参考：https://blog.csdn.net/zkk9527/article/details/89792602
    Vector2d b = Vector2d(t.dot(f_ref), t.dot(f2));
    Matrix2d A;
    A(0, 0) = f_ref.dot(f_ref);  //
    A(0, 1) = -f_ref.dot(f2);
    A(1, 0) = -A(0, 1);
    A(1, 1) = -f2.dot(f2);
    Vector2d ans = A.inverse() * b;
    Vector3d xm = ans[0] * f_ref;           // ref 侧的结果
    Vector3d xn = t + ans[1] * f2;          // cur 结果
    Vector3d p_esti = (xm + xn) / 2.0;      // P的位置，取两者的平均
    double depth_estimation = p_esti.norm();   //（mu_obs）深度值

    // 计算不确定性（以一个像素为误差）
    Vector3d p = f_ref * depth_estimation;
    Vector3d a = p - t;
    double t_norm = t.norm();
    double a_norm = a.norm();
    double alpha = acos(f_ref.dot(t) / t_norm);
    double beta = acos(-a.dot(t) / (a_norm * t_norm));
    Vector3d f_curr_prime = px2cam(pt_curr + epipolar_direction);
    f_curr_prime.normalize();
    double beta_prime = acos(f_curr_prime.dot(-t) / t_norm);
    double gamma = M_PI - alpha - beta_prime;
    double p_prime = t_norm * sin(beta_prime) / sin(gamma);
    double d_cov = p_prime - depth_estimation;   //(sigma_obs)这里为什么是反的？因为要平方吗？
    double d_cov2 = d_cov * d_cov;

    // 高斯融合 P312 式12.6
   // 这个循环是针对某一对匹配的点而言，计算估计其深度值mu_obs，深度估计的方差sigma_obs^2，用于更新整张图中此点的深度均值mu和方差sigma
    double mu = depth.ptr<double>(int(pt_ref(1, 0)))[int(pt_ref(0, 0))];  //这个数据结构是用指针访问图像的像素，第int(pt_ref(1, 0))行的第int(pt_ref(0, 0))列个像素
    double sigma2 = depth_cov2.ptr<double>(int(pt_ref(1, 0)))[int(pt_ref(0, 0))];

    double mu_fuse = (d_cov2 * mu + sigma2 * depth_estimation) / (sigma2 + d_cov2);
    double sigma_fuse2 = (sigma2 * d_cov2) / (sigma2 + d_cov2);

    depth.ptr<double>(int(pt_ref(1, 0)))[int(pt_ref(0, 0))] = mu_fuse;
    depth_cov2.ptr<double>(int(pt_ref(1, 0)))[int(pt_ref(0, 0))] = sigma_fuse2;

    return true;
}

// 后面这些太简单我就不注释了（其实是因为懒）
void plotDepth(const Mat &depth_truth, const Mat &depth_estimate) {
    imshow("depth_truth", depth_truth * 0.4);
    imshow("depth_estimate", depth_estimate * 0.4);
    imshow("depth_error", depth_truth - depth_estimate);
    waitKey(1);
}

void evaludateDepth(const Mat &depth_truth, const Mat &depth_estimate) {
    double ave_depth_error = 0;     // 平均误差
    double ave_depth_error_sq = 0;      // 平方误差
    int cnt_depth_data = 0;
    for (int y = boarder; y < depth_truth.rows - boarder; y++)
        for (int x = boarder; x < depth_truth.cols - boarder; x++) {
            double error = depth_truth.ptr<double>(y)[x] - depth_estimate.ptr<double>(y)[x];
            ave_depth_error += error;
            ave_depth_error_sq += error * error;
            cnt_depth_data++;
        }
    ave_depth_error /= cnt_depth_data;
    ave_depth_error_sq /= cnt_depth_data;

    cout << "Average squared error = " << ave_depth_error_sq << ", average error: " << ave_depth_error << endl;
}

void showEpipolarMatch(const Mat &ref, const Mat &curr, const Vector2d &px_ref, const Vector2d &px_curr) {
    Mat ref_show, curr_show;
    cv::cvtColor(ref, ref_show, CV_GRAY2BGR);
    cv::cvtColor(curr, curr_show, CV_GRAY2BGR);

    cv::circle(ref_show, cv::Point2f(px_ref(0, 0), px_ref(1, 0)), 5, cv::Scalar(0, 0, 250), 2);
    cv::circle(curr_show, cv::Point2f(px_curr(0, 0), px_curr(1, 0)), 5, cv::Scalar(0, 0, 250), 2);

    imshow("ref", ref_show);
    imshow("curr", curr_show);
    waitKey(1);
}

void showEpipolarLine(const Mat &ref, const Mat &curr, const Vector2d &px_ref, const Vector2d &px_min_curr,
                      const Vector2d &px_max_curr) {

    Mat ref_show, curr_show;
    cv::cvtColor(ref, ref_show, CV_GRAY2BGR);
    cv::cvtColor(curr, curr_show, CV_GRAY2BGR);

    cv::circle(ref_show, cv::Point2f(px_ref(0, 0), px_ref(1, 0)), 5, cv::Scalar(0, 255, 0), 2);
    cv::circle(curr_show, cv::Point2f(px_min_curr(0, 0), px_min_curr(1, 0)), 5, cv::Scalar(0, 255, 0), 2);
    cv::circle(curr_show, cv::Point2f(px_max_curr(0, 0), px_max_curr(1, 0)), 5, cv::Scalar(0, 255, 0), 2);
    cv::line(curr_show, Point2f(px_min_curr(0, 0), px_min_curr(1, 0)), Point2f(px_max_curr(0, 0), px_max_curr(1, 0)),
             Scalar(0, 255, 0), 1);

    imshow("ref", ref_show);
    imshow("curr", curr_show);
    waitKey(1);
}

1.2 单目稠密重建讨论

1. 像素梯度：像素梯度与极线平行时能精确匹配，而垂直时，匹配程度相同，无法正确匹配，故：像素梯度与极线夹角较大时，极线匹配的不确定性大；夹角较小时，匹配的不确定性变小。
2. 逆深度：深度d实际上步步和Gaussian分布，而逆深度$\frac{1}{d}$比较符合。
3. 图相间的变换：如果相机发生旋转，上黑下白变成上白下黑，相关性就会变成负数，无法正常匹配。为了解决这种问题，需要在块匹配前把参考帧与当前帧的运动考虑进来，在局部范围内构造一个参考帧和当前帧坐标变换的一个仿射变换（教材 $P_{326-327}$ 12.3.4节），可以将当前帧（或参考帧）的像素进行变换，在进行块匹配，以期获得对旋转更好的效果。
4. 并行化：由程序可以看出，针对每个像素的深度估计，在一个二重循环中遍历每个像素进行估计，但是每个像素估计之间是相互独立的，结果不会对对方产生影响，故此过程可以并行化，使用GPU来进行加速。
5. 其他改进：
   1. 上述的深度估计可能在相邻的像素点间存在跳变的现象，深度估计不够平滑，可以给深度估计加上空间正则化项，使得深度图更加平滑。
   2. 没有显式地处理外点，只是用NCC阈值对匹配进行了筛选，当出现误匹配时对深度估计会有影响。
   3. 处理误匹配如均匀-高斯混合分布下的深度滤波器，将内点和外点进行区别并进行概率建模。

单目稠密重建在理论上仍有一些困难，如对环境纹理的依赖，像素梯度与极线方向的关联，这些问题很难通过工程手段来解决，所以双目和移动单目的稠密重建的地图过度依赖环境纹理和光照，不够可靠。

2. RGB-D稠密建图

2.1 点云地图

这个在我电脑上编译不通过，google半天也不知道为什么会出这个错误，先放这里。

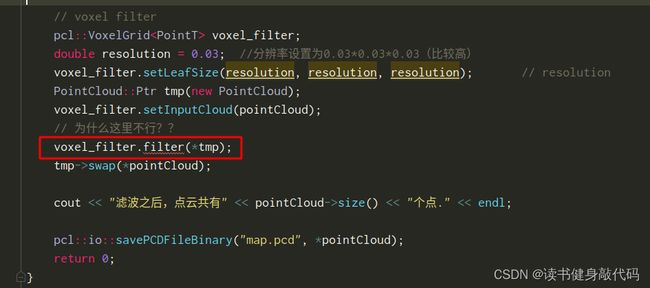
上面是在点云建图的基础上增加了一些滤波处理，包括

1. 滤除深度无效的点（判断深度是否为0）；
2. 利用统计滤波滤除孤立点；
3. 利用体素滤波进行降采样。（bug出在体素滤波这里，不知为何）
   总之，点云地图作为一种初级的地图，尚无法满足定位，导航与避障，可视化和交互等功能，但是可从点云地图出发，进行进一步处理，使其满足对应的需求。

2.2 从点云重建网络

由于上面的代码没跑通，使用之前第5章的房间的点云地图来进行此部分实验。
之前的点云：

远处看还可以，但是近处看都是一系列点，没有什么实际用处，故需要进行处理。

本部分思路是先计算点云的法线，再从法线计算网格。

代码：

//
// Created by gaoxiang on 19-4-25.
//

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

// typedefs
typedef pcl::PointXYZRGB PointT;
typedef pcl::PointCloud<PointT> PointCloud;
typedef pcl::PointCloud<PointT>::Ptr PointCloudPtr;
typedef pcl::PointXYZRGBNormal SurfelT;
typedef pcl::PointCloud<SurfelT> SurfelCloud;
typedef pcl::PointCloud<SurfelT>::Ptr SurfelCloudPtr;

SurfelCloudPtr reconstructSurface(const PointCloudPtr &input, float radius, int polynomial_order)
{
    pcl::MovingLeastSquares<PointT, SurfelT> mls;
    pcl::search::KdTree<PointT>::Ptr tree(new pcl::search::KdTree<PointT>);
    mls.setSearchMethod(tree);
    mls.setSearchRadius(radius);
    mls.setComputeNormals(true);
    mls.setSqrGaussParam(radius * radius);
    mls.setPolynomialFit(polynomial_order > 1);
    mls.setPolynomialOrder(polynomial_order);
    mls.setInputCloud(input);
    SurfelCloudPtr output(new SurfelCloud);
    mls.process(*output);
    return (output);
}

pcl::PolygonMeshPtr triangulateMesh(const SurfelCloudPtr &surfels)
{
    // Create search tree*  创建搜索树
    pcl::search::KdTree<SurfelT>::Ptr tree(new pcl::search::KdTree<SurfelT>);
    tree->setInputCloud(surfels);

    // Initialize objects
    pcl::GreedyProjectionTriangulation<SurfelT> gp3;
    pcl::PolygonMeshPtr triangles(new pcl::PolygonMesh);

    // Set the maximum distance between connected points (maximum edge length) 设置两点之间的最大距离
    gp3.setSearchRadius(0.05);

    // Set typical values for the parameters  设置常规参数
    gp3.setMu(2.5);
    gp3.setMaximumNearestNeighbors(100);  //最大；临近点个数
    gp3.setMaximumSurfaceAngle(M_PI / 4); // 45 degrees  最大表面角
    gp3.setMinimumAngle(M_PI / 18); // 10 degrees  最小角
    gp3.setMaximumAngle(2 * M_PI / 3); // 120 degrees  最大角
    gp3.setNormalConsistency(true);

    // Get result
    gp3.setInputCloud(surfels);  //输入
    gp3.setSearchMethod(tree);  //设置方法
    gp3.reconstruct(*triangles);  //重建

    return triangles;
}

int main(int argc, char **argv)
{
    // Load the points
    PointCloudPtr cloud(new PointCloud);
    if (argc == 0 || pcl::io::loadPCDFile(argv[1], *cloud)) {
        cout << "failed to load point cloud!";
        return 1;
    }
    cout << "point cloud loaded, points: " << cloud->points.size() << endl;

    // Compute surface elements
    cout << "computing normals ... " << endl;
    double mls_radius = 0.05, polynomial_order = 2;
    auto surfels = reconstructSurface(cloud, mls_radius, polynomial_order);  //surfel重建，计算surfel面片

    // Compute a greedy surface triangulation 计算贪婪表面的三角化
    cout << "computing mesh ... " << endl;
    pcl::PolygonMeshPtr mesh = triangulateMesh(surfels);  //获得三角网格重建

    cout << "display mesh ... " << endl;
    pcl::visualization::PCLVisualizer vis;
    vis.addPolylineFromPolygonMesh(*mesh, "mesh frame");
    vis.addPolygonMesh(*mesh, "mesh");
    vis.resetCamera();
    vis.spin();
}

这部分代码没什么注释，看不太懂，先知道这是个什么东西，暂时略过。

重建之后如下图：

这个跟点云的对比就比较明显了，把点连成了一个个小面，原本没有表面信息的点云构建出了法线，纹理等信息了，点云地图转换成了网格地图。（这里的点云重建算法是Moving Least Square和 Greedy Projection移动最小二乘和贪心投影？？）

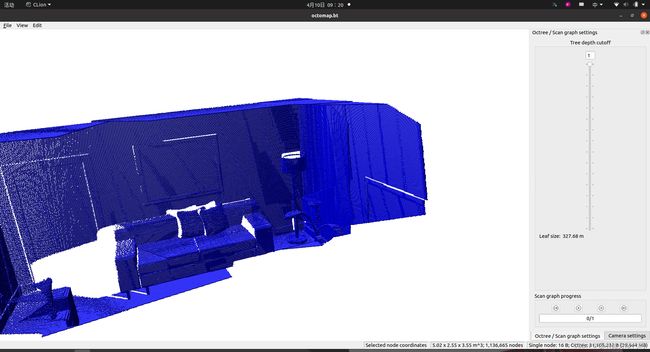
2.3 八叉树地图

需要安装octomap库和octovis可视化工具，在Ubuntu的仓库中均有。

分辨率越高，八叉树地图的文件大小越大，但地图越细致，这也符合常识。

这是0.01分辨率的地图，将近30M：

这是0.1的分辨率的地图（有点我的世界的味道了~），这里的大小只有一个0.27M，小了快100倍（虽然可能跟分辨率确实没有什么直接关系）。

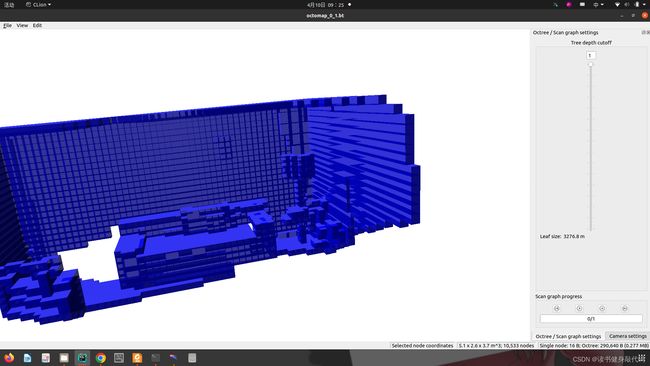
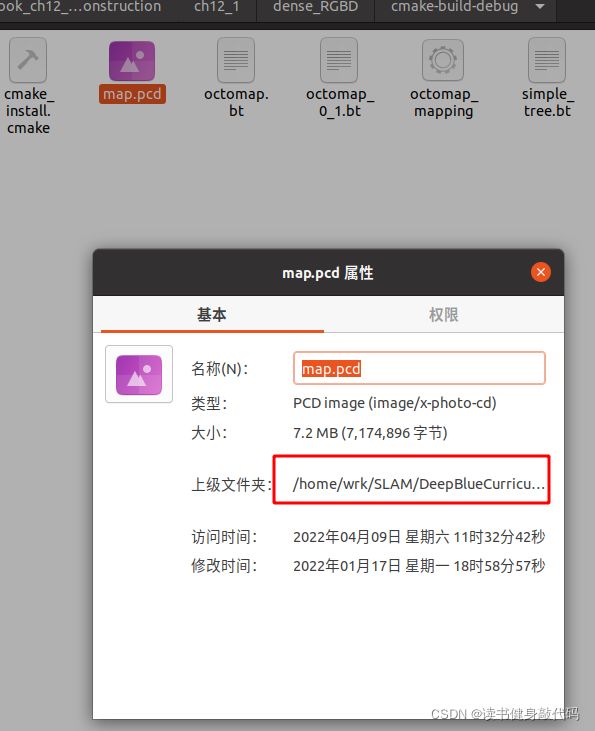
但是 确实比之前的点云地图小很多，第5章的点云地图有7.2M

3. TSDF地图和fusion系列

之前的建图中主要以定位为主，地图的拼接是作为后续加工步骤放在SLAM框架中的，是因为SLAM要求实时性，定位算法一般能够满足实时性要求（尤其是使用稀疏特征或者稀疏直接法时），而地图的表达和存储往往需要较大计算量，不适合实时处理。

当然，也存在以“建图”为主体，“定位”居于此要地位的做法，即“实时三维重建（SfM）”，都使用RGB-D图像。当地图为主要目标时，就需要使用GPU来加速计算，需要较重的计算设备，实时重建正在朝大规模、大型动态场景的重建方向发展；而SLAM超轻量级，小型化方向发展，有方案甚至放弃了建图和回环检测部分，只保留了视觉里程计。

经典的实时三维重建算法有TSDF（译为“截断符号距离函数”，有些怪怪的，还是叫TSDF吧）。与八叉树类似，TSDF是一种网格式地图，每个TSDF体素内存储了该小块与距其最近的物体表面的距离，TSDF值由负号变为正号的地方就是物体的表面。这是对于TSDF最简单的理解。

4. 小结

本章介绍了一些常见的地图形式，稀疏路标地图，稠密地图，语义地图等。对稠密地图进行了较为详细的讨论，主要包括单目稠密重建和RGB-D稠密重建，单目稠密重建需要先估计深度，介绍了高斯分布的深度滤波器，步骤是

1. 假设深度服从高斯分布
2. 极限搜索和块匹配(相当于特征匹配，只不过像素太多，无法计算所有的描述子)
3. 三角化估计深度
4. 将本次估计与之前的估计进行高斯融合
   在实践环节使用200张图片迭代的方式对第一章图片的深度图进行了估计（有bug没有跑通…）。
   同时在讨论部分我们讨论了单目深度估计的像素梯度问题，逆深度问题，块匹配之前的图像间的变换（解决单目的旋转问题），并行化（效率问题，各个像素见得深度估计互不影响，可以并行化），处理误匹配点的问题。且讨论了单目和双目过度依赖环境纹理和光照，不够可靠。

于是引入了RGB-D稠密重建，直接可以硬件获得较为准确的深度图，无需估计，

在RGB-D稠密重建的实践部分我们建立了点云地图，相较于第5章，我们新加入了

1. 对深度的判断；
2. 使用统计滤波去除孤立点；
3. 使用体素滤波进行降采样以节省存储空间。

尽管进行了降采样，但是点云地图仍然较大，存储了一些不必要的细节信息（如地毯的褶皱等），于是引入了八叉树地图，可以很大程度上缩小地图所占的存储空间，其节点存储了是否被占据的信息。

到此为止的建图都是以定位为主体，建图为次要的框架，接下来介绍了以建图为主体的框架：（使用RGB-D图像的）实时三维重建。实时三维重建计算量大，需要GPU支持，网大规模发展，介绍了一种典型的实时三维重建地图形式：TSDF。

需要说明，本讲介绍的地图偏重于度量地图，而拓扑地图形式和SLAM研究差别较大，没有展开讨论（目前对拓扑地图还不是非常了解）。

本章笔记完。