机器学习实战——python实现DBSCAN密度聚类

基础概念

 ε-邻域：对于样本集中的xj, 它的ε-邻域为样本集中与它距离小于ε的样本所构成的集合。 
 核心对象：若xj的ε-邻域中至少包含MinPts个样本，则xj为一个核心对象。 
 密度直达：若xj位于xi的ε-邻域中，且xi为核心对象，则xj由xi密度直达。 
 密度可达：若样本序列p1, p2, ……, pn。pi+1由pi密度直达，则p1由pn密度可达。

算法过程

输入：样本集D={x1,x2,...,xm}
    邻域参数(ε,MinPts).
过程：
初始化核心对象集合：Ω = Ø
for j=1,2,...,m do
    确定样本xj的ε-邻域N(xj);
    if |N(xj)|>=MinPts then
        将样本xj加入核心对象集合Ω
    end if
end for
初始化聚类簇数：k=0
初始化未访问样本集合：Γ =D
while Ω != Ø do
    记录当前未访问样本集合：Γold = Γ;
    随机选取一个核心对象 o ∈ Ω，初始化队列Q=
    Γ = Γ\{o};
    while Q != Ø do
        取出队列Q中首个样本q;
        if |N(q)|<=MinPts then
            令Δ = N(q)∩Γ；
            将Δ中的样本加入队列Q;
            Γ = Γ\Δ；
        end if
    end while
    k = k+1,生成聚类簇Ck = Γold\Γ;
    Ω = Ω\Ck
end while
输出：
簇划分C = {C1,C2,...,Ck}

算法实现

#计算两个向量之间的欧式距离
def calDist(X1 , X2 ):
    sum = 0
    for x1 , x2 in zip(X1 , X2):
        sum += (x1 - x2) ** 2
    return sum ** 0.5

#获取一个点的ε-邻域（记录的是索引）
def getNeibor(data , dataSet , e):
    res = []
    for i in range(shape(dataSet)[0]):
        if calDist(data , dataSet[i])return res

#密度聚类算法
def DBSCAN(dataSet , e , minPts):
    coreObjs = {}#初始化核心对象集合
    C = {}
    n = shape(dataSet)[0]
    #找出所有核心对象，key是核心对象的index，value是ε-邻域中对象的index
    for i in range(n):
        neibor = getNeibor(dataSet[i] , dataSet , e)
        if len(neibor)>=minPts:
            coreObjs[i] = neibor   
    oldCoreObjs = coreObjs.copy()
    k = 0#初始化聚类簇数
    notAccess = range(n)#初始化未访问样本集合（索引）
    while len(coreObjs)>0:
        OldNotAccess = []
        OldNotAccess.extend(notAccess)
        cores = coreObjs.keys()
        #随机选取一个核心对象
        randNum = random.randint(0,len(cores))
        core = cores[randNum]
        queue = []
        queue.append(core)
        notAccess.remove(core)
        while len(queue)>0:
            q = queue[0]
            del queue[0]
            if q in oldCoreObjs.keys() :    
                delte = [val for val in oldCoreObjs[q] if val in notAccess]#Δ = N(q)∩Γ                
                queue.extend(delte)#将Δ中的样本加入队列Q                
                notAccess = [val for val in notAccess if val not in delte]#Γ = Γ\Δ
        k += 1
        C[k] = [val for val in OldNotAccess if val not in notAccess]
        for x in C[k]:
            if x in coreObjs.keys():
                del coreObjs[x]
    return C

结果测试

测试数据（来源于西瓜书）

0.697,0.46
0.774,0.376
0.634,0.264
0.608,0.318
0.556,0.215
0.403,0.237
0.481,0.149
0.437,0.211
0.666,0.091
0.243,0.267
0.245,0.057
0.343,0.099
0.639,0.161
0.657,0.198
0.36,0.37
0.593,0.042
0.719,0.103
0.359,0.188
0.339,0.241
0.282,0.257
0.748,0.232
0.714,0.346
0.483,0.312
0.478,0.437
0.525,0.369
0.751,0.489
0.532,0.472
0.473,0.376
0.725,0.445
0.446,0.459

数据处理

def loadDataSet(fileName):
    dataMat = []
    fr = open(fileName)
    for line in fr.readlines():
        curLine = line.strip().split(' ')
        fltLine = map(float,curLine)
        dataMat.append(fltLine)
    return dataMat

画图方法

def draw(C , dataSet):
    color = ['r', 'y', 'g', 'b', 'c', 'k', 'm']
    for i in C.keys():
        X = []
        Y = []
        datas = C[i]
        for j in range(len(datas)):
            X.append(dataSet[datas[j]][0])
            Y.append(dataSet[datas[j]][1])
        plt.scatter(X, Y, marker='o', color=color[i % len(color)], label=i)
    plt.legend(loc='upper right')
    plt.show()

测试代码

按照西瓜书设置的ε和MinPts参数

dataSet = loadDataSet("dataSet.txt")
C = DBSCAN(dataSet , 0.11 , 5)
draw(C , dataSet)

聚类结果

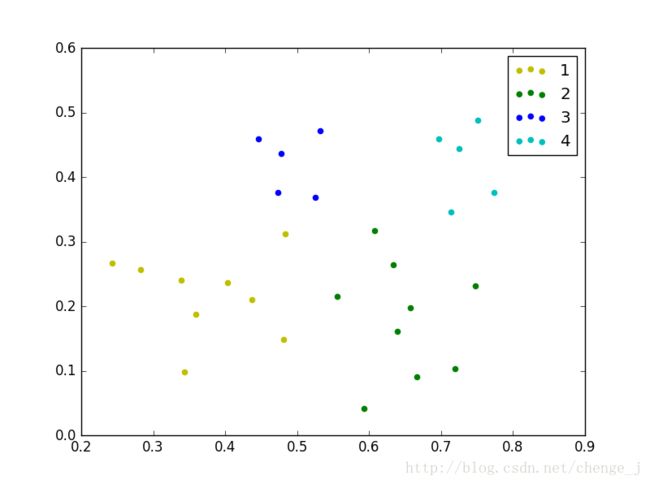
由于是随机选取核心对象，所以每次运行可能获得不同的聚类结果。