高斯混合模型（GMM）

高斯混合模型

k-means 聚类模型非常简单并且易于理解，但是它的简单性也为实际应用带
来了挑战。特别是在实际应用中，k-means 的非概率性和它仅根据到簇中心点的距离来指
派簇的特点将导致性能低下。这一节将介绍高斯混合模型，该模型可以被看作是k-means
思想的一个扩展，但它也是一种非常强大的聚类评估工具。还是从标准导入开始：

%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np

高斯混合模型（GMM）为什么会出现：k-means

算法的缺陷
下面来介绍一些k-means 算法的不足之处，并思考如何改进我们的聚类模型。就像前一节
所看到的，只要给定简单且分离性非常好的数据，k-means 就可以找到合适的聚类结果。
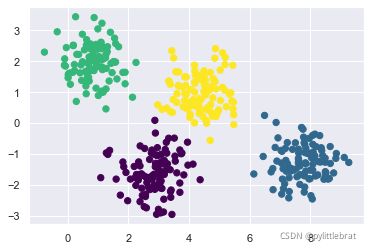
例如，只要有简单的数据簇，k-means 算法就可以快速给这些簇作标记，标记结果和通过
肉眼观察到的簇的结果十分接近：

from sklearn.datasets import make_blobs
X, y_true = make_blobs(n_samples=400, centers=4,
cluster_std=0.60, random_state=0)
X = X[:, ::-1] # 交换列是为了方便画图
#用k-means标签画出数据
from sklearn.cluster import KMeans
kmeans = KMeans(4, random_state=0)
labels = kmeans.fit(X).predict(X)
plt.scatter(X[:, 0], X[:, 1], c=labels, s=40, cmap='viridis');

簇似乎有一小块区域重合，因此我们对重合部分的点将被分配到哪个簇不是很有信心。不
幸的是，k-means 模型本身也没有度量簇的分配概率或不确定性的方法（虽然可以用数据
重抽样方法bootstrap 来估计不确定性）。因此，我们必须找到一个更通用的模型。
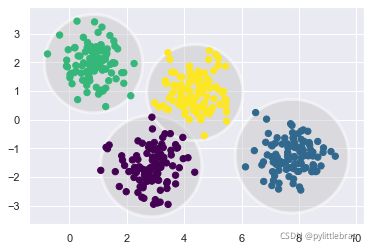
理解k-means 模型的一种方法是，它在每个簇的中心放置了一个圆圈（在更高维空间中是
一个超空间），圆圈半径根据最远的点与簇中心点的距离算出。这个半径作为训练集分配
簇的硬切断（hard cutoff），即在这个圆圈之外的任何点都不是该簇的成员。可以用以下函
数将这个聚类模型可视化：

from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
def plot_kmeans(kmeans, X, n_clusters=4, rseed=0, ax=None):
    labels = kmeans.fit_predict(X)
    # 画出输入数据
    ax = ax or plt.gca()
    ax.axis('equal')
    ax.scatter(X[:, 0], X[:, 1], c=labels, s=40, cmap='viridis', zorder=2)
    # 画出k-means模型的表示
    centers = kmeans.cluster_centers_
    radii = [cdist(X[labels == i], [center]).max() for i, center in enumerate(centers)]
    for c, r in zip(centers, radii):
        ax.add_patch(plt.Circle(c, r, fc='#CCCCCC', lw=3, alpha=0.5, zorder=1))
kmeans = KMeans(n_clusters=4, random_state=0)
plot_kmeans(kmeans, X)

k-means 有一个重要特征，它要求这些簇的模型必须是圆形：k-means 算法没有内置的方法
来实现椭圆形的簇。因此，如果对同样的数据进行一些转换，簇的分配就会变得混乱：

rng = np.random.RandomState(13)
X_stretched = np.dot(X, rng.randn(2, 2))
kmeans = KMeans(n_clusters=4, random_state=0)
plot_kmeans(kmeans, X_stretched)

通过肉眼观察，可以发现这些变形的簇并不是圆形的，因此圆形的簇拟合效果非常糟糕。
总之，k-means 对这个问题有点无能为力，只能强行将数据拟合至4 个圆形的簇，但却导
致多个圆形的簇混在一起、相互重叠，右下部分尤其明显。有人可能会想用PCA（详情请
参见5.9 节）先预处理数据，从而解决这个特殊的问题。但实际上，PCA 也不能保证这样
的全局操作不会导致单个数据被圆形化。
k-means 的这两个缺点——类的形状缺少灵活性、缺少簇分配的概率——使得它对许多数
据集（特别是低维数据集）的拟合效果不尽如人意。
你可能想通过对k-means 模型进行一般化处理来弥补这些不足，例如可以通过比较每个点
与所有簇中心点的距离来度量簇分配的不确定性，而不仅仅是关注最近的簇。你也可能想
通过将簇的边界由圆形放宽至椭圆形，从而得到非圆形的簇。实际上，这正是另一种的聚
类模型——高斯混合模型——的两个基本组成部分。

一般化E-M：高斯混合模型

一个高斯混合模型（Gaussian mixture model，GMM）试图找到多维高斯概率分布的混合
体，从而获得任意数据集最好的模型。在最简单的场景中，GMM 可以用与k-means 相同
的方式寻找类：

from sklearn.mixture import GaussianMixture as GMM
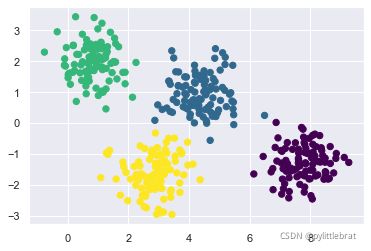
gmm = GMM(n_components=4).fit(X)
labels = gmm.predict(X)
plt.scatter(X[:, 0], X[:, 1], c=labels, s=40, cmap='viridis');

但由于GMM 有一个隐含的概率模型，因此它也可能找到簇分配的概率结果——在Scikit-
Learn 中用predict_proba 方法实现。这个方法返回一个大小为[n_samples, n_clusters]
的矩阵，矩阵会给出任意点属于某个簇的概率：

probs = gmm.predict_proba(X)
print(probs[:5].round(3))

[[0.469 0.531 0.    0.   ]
 [0.    0.    0.    1.   ]
 [0.    0.    0.    1.   ]
 [0.    1.    0.    0.   ]
 [0.    0.    0.    1.   ]]

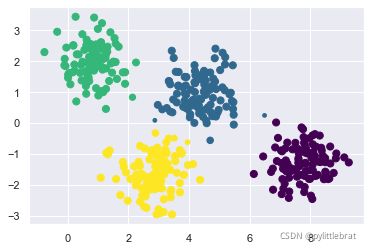
我们可以将这个不确定性可视化，用每个点的大小体现预测的不确定性，使其成正比.在簇边界上的点反映了簇分配的不确定性：

size = 50 * probs.max(1) ** 2 # 平方强调差异
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', s=size);

高斯混合模型本质上和k-means 模型非常类似，它们都使用了期望最大化方法，具体实现
如下。

1. 选择初始簇的中心位置和形状。
2. 重复直至收敛。

• 期望步骤（E-step）：为每个点找到对应每个簇的概率作为权重。
• 最大化步骤（M-step）：更新每个簇的位置，将其标准化，并且基于所有数据点的权重来确定形状。

最终结果表明，每个簇的结果并不与硬边缘的空间（hard-edged sphere）有关，而是通过高
斯平滑模型实现。正如在k-means 中的期望最大化方法，这个算法有时并不是全局最优解，
因此在实际应用需要使用多个随机初始解。
下面创建一个可视化GMM 簇位置和形状的函数，该函数用gmm 的输出结果画出椭圆：

from matplotlib.patches import Ellipse

def draw_ellipse(position, covariance, ax=None, **kwargs):
    """Draw an ellipse with a given position and covariance"""
    ax = ax or plt.gca()
    
    # Convert covariance to principal axes
    if covariance.shape == (2, 2):
        U, s, Vt = np.linalg.svd(covariance)
        angle = np.degrees(np.arctan2(U[1, 0], U[0, 0]))
        width, height = 2 * np.sqrt(s)
    else:
        angle = 0
        width, height = 2 * np.sqrt(covariance)
    
    # Draw the Ellipse
    for nsig in range(1, 4):
        ax.add_patch(Ellipse(position, nsig * width, nsig * height,
                             angle, **kwargs))
        
def plot_gmm(gmm, X, label=True, ax=None):
    ax = ax or plt.gca()
    labels = gmm.fit(X).predict(X)
    if label:
        ax.scatter(X[:, 0], X[:, 1], c=labels, s=40, cmap='viridis', zorder=2)
    else:
        ax.scatter(X[:, 0], X[:, 1], s=40, zorder=2)
    ax.axis('equal')
    
    w_factor = 0.2 / gmm.weights_.max()
    for pos, covar, w in zip(gmm.means_, gmm.covars_, gmm.weights_):
        draw_ellipse(pos, covar, alpha=w * w_factor)

gmm = GMM(n_components=4, random_state=42)
# plot_gmm(gmm, X)