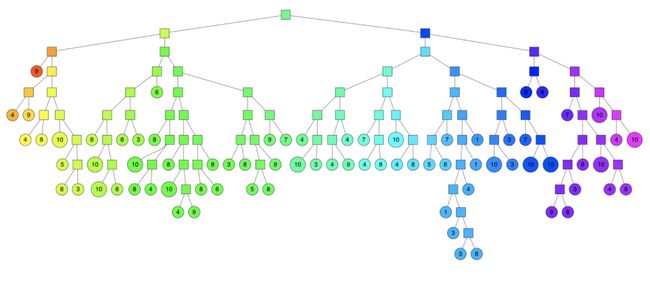
机器学习算法系列(二十二)-近似k近邻算法-Annoy(Approximate Nearest Neighbor / ANN)
阅读本文需要的背景知识点:k近邻算法、一丢丢编程知识
一、引言
前面一节我们学习了机器学习算法系列(二十一)-k近邻算法(k-Nearest Neighbor / kNN Algorithm),其中介绍了两种查询最近的 k 个样本点的算法——k-维树(k-d tree)与Ball 树(Ball tree)。
上面两种算法在样本不大、维度不多的情况下,可以精确快速地查询出最近邻,但是现实中往往都是百万级以上样本,数百维特征的数据集,上述的算法在某些应用场景下逐渐无法满足实时查询的要求,当该应用场景对搜索的精确性没有那么高的要求时,可以通过牺牲一些准确度来换取快速查询的性能,这就是所谓的近似 k 近邻算法1 (Approximate Nearest Neighbor / ANN)。
近似 k 近邻的算法有很多,下面分三篇文章分别介绍三个有代表性的算法,这一节先来看看一种基于树的算法——Annoy2(Approximate Nearest Neighbors Oh Yeah)。
二、模型介绍
Annoy 算法是由 Erik Bernhardsson 在 Hack Week 期间用几个下午构建出来的,被应用于著名音乐应用 Spotify 的音乐推荐中,其结构与上一节中提到的 k-维树(k-d tree)与 Ball 树(Ball tree)一样,也是一种基于二叉树结构的算法。
Annoy 二叉树构建
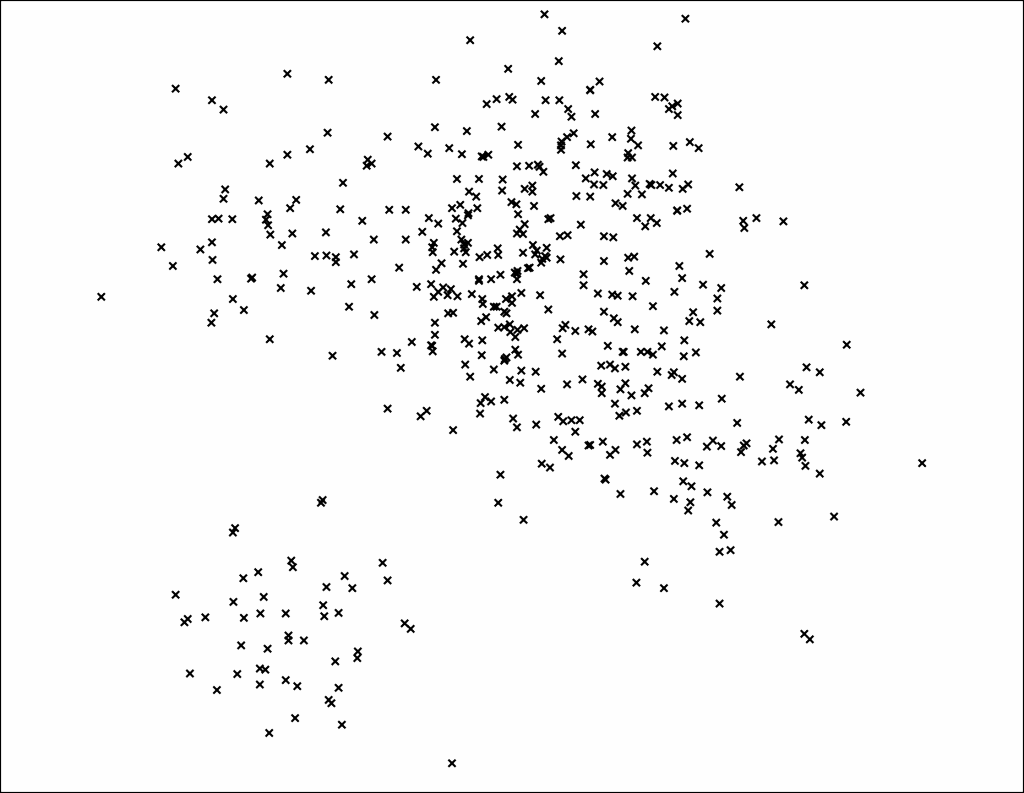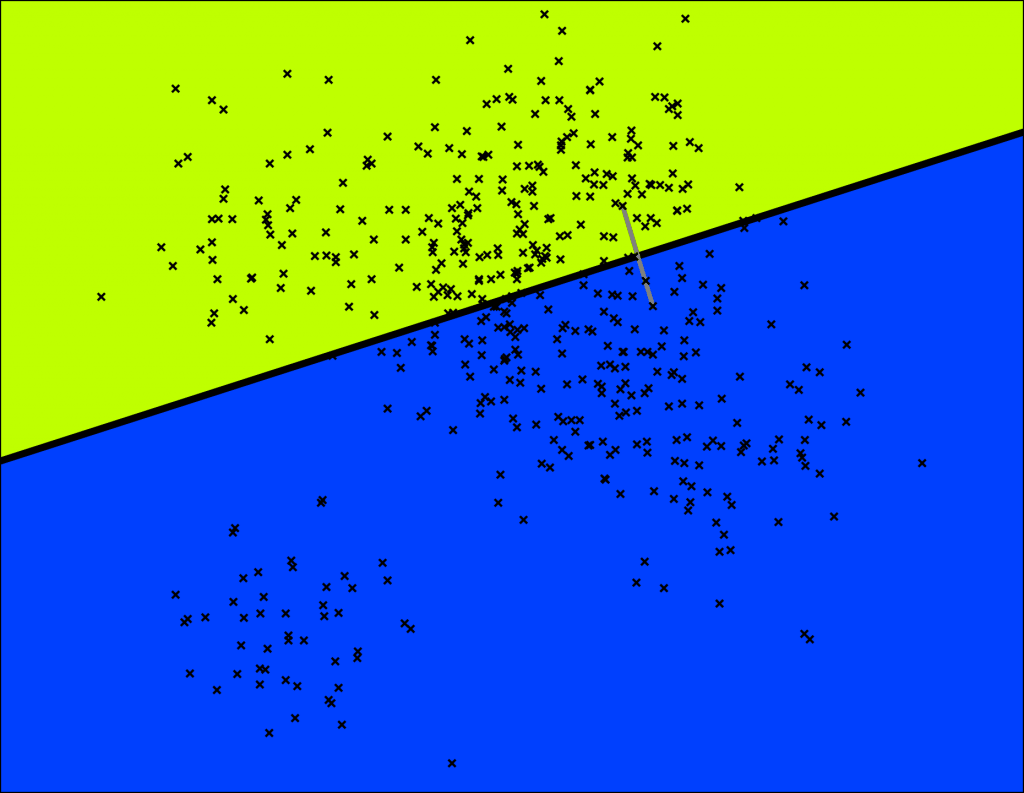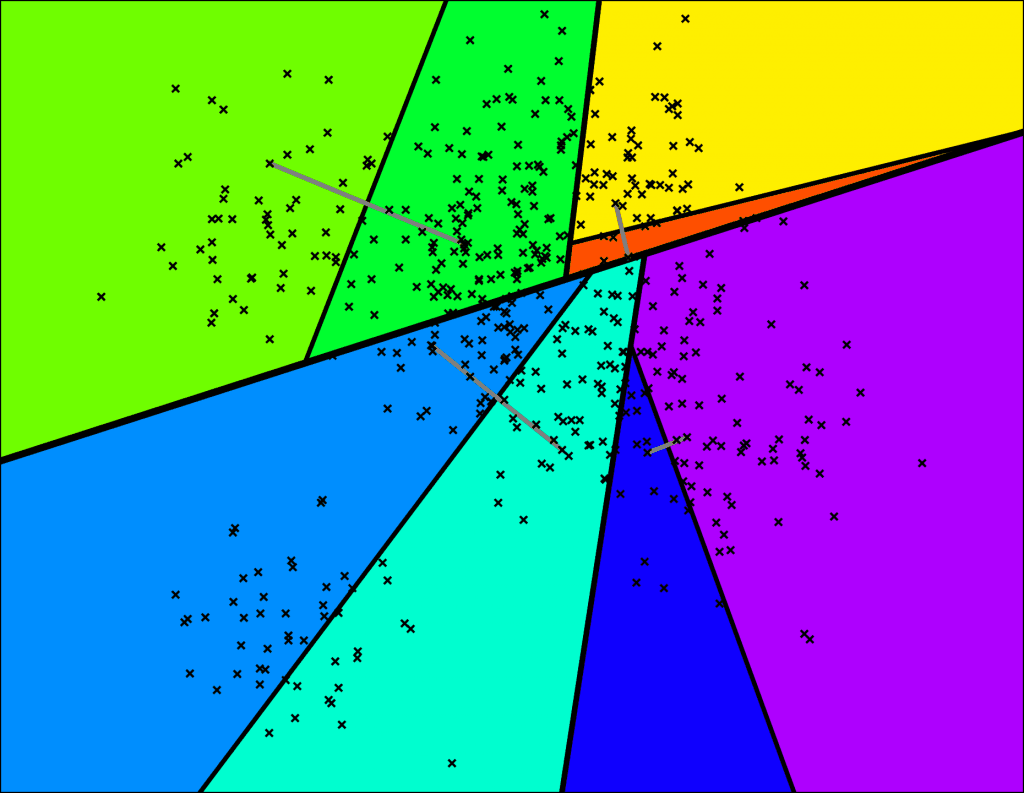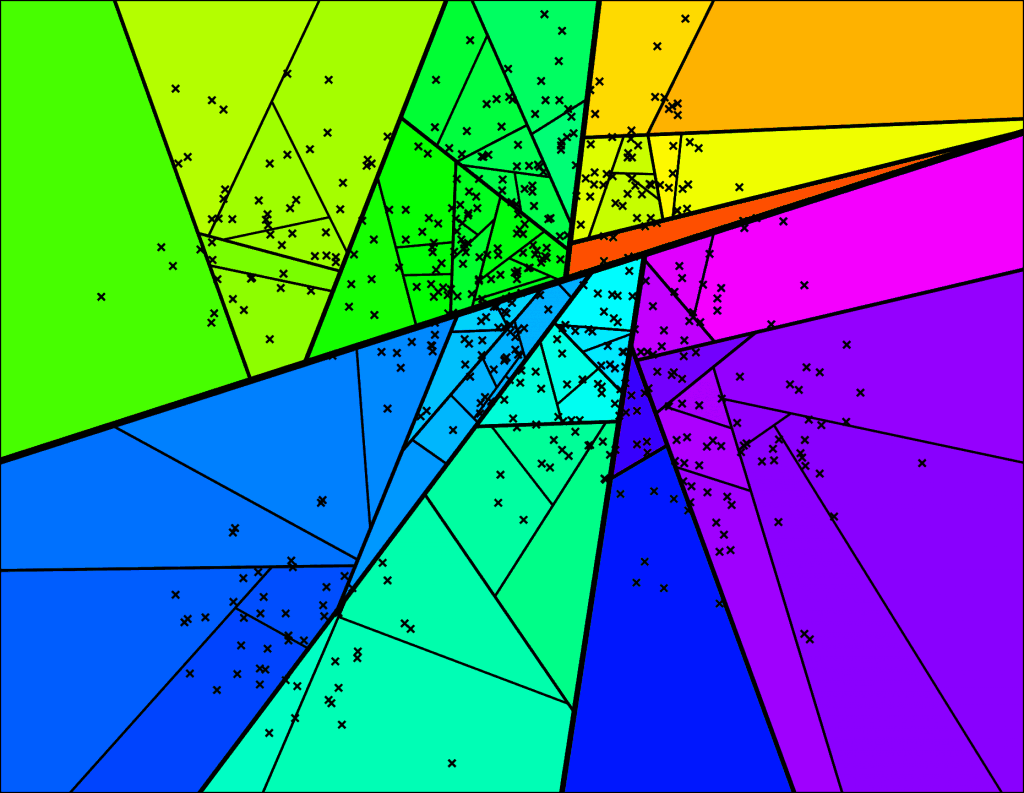
首先随机选取两个样本点,构建一个与这两个样本点 P、Q 等距的超平面(图中的粗黑线)作为分割平面,然后依次递归地进行分割,直到样本点无法被分割或剩余样本点小于等于指定的数量为止。
结点超平面的法向量为:
w = P − Q w = P - Q w=P−Q
结点超平面的偏移量为 :
b = − P + Q 2 w b = - \frac{P + Q}{2}w b=−2P+Qw
最后得到一棵二叉树如图 2-2 所示:
查询 k 近邻
查询 k 近邻时只需顺着二叉树由上至下找到对应的叶子结点即可。但是上面的查询方式会产生几个问题:
- 当最近点刚好在划分超平面的外面怎么办?
- 当要查询的近邻数量大于叶子结点中包含的样本数量怎么办?
针对上面两个问题,其中一种优化的技巧是使用优先级队列,不再只查下一个叶子结点,而是按照距离的优先级,多查询几个叶子结点。另一种优化技巧是构造一片由多棵二叉树组成的森林,查询时同时搜索所有的二叉树。组合上面两种优化方法后的搜索过程如图 2-3 所示:
最后的搜索范围组合后如图 2-4 所示,最后在搜索范围内查询 k 近邻。

Annoy 二叉树平衡
在构造单棵二叉树运气不好时,每次随机选取的两点都靠近数据集的边缘,构造出的树极度不平衡,导致树的深度过深,会影响搜索时的效率,annoy 算法不是简单的随机选取两个点,而是通过一种启发式的方法来平衡二叉树两边的子树,步骤如下图 2-5 所示:

首先在样本集中随机选取两个点(如图中的点 P、Q),再在样本集中随机选择一个目标点 T,计算点 P、Q 与点 T 的距离,取距离近的点向目标点移动,移动的距离取决于循环的次数。重复以上操作,最后得到平衡后的 P、Q 两点,具体的算法可参考下面的代码实现或 Annoy 的源码。
更多详细的算法演示请参考 Annoy 作者的博客文章介绍3,上面的大部分图片同样出自该文章。
三、算法步骤
Annoy 构建
- 启发式的选取两个样本点
- 计算并记录与两个样本点等距的超平面,作为一个结点
- 根据样本点在超平面的位置决定被分配到哪一边的子树中
- 当样本点无法被分割或剩余样本点小于等于指定的数量时,结束算法
- 重复上述步骤,构建多棵二叉树
查询 k 近邻
- 将所有二叉树的根结点插入到优先级队列中
- 按优先级搜索队列中所有的结点,直到搜索到了指定次数的结点
- 去除重复的样本点
- 计算距离排序后返回最近的 k 近邻
四、原理证明
超平面的偏移量
(1)超平面的表达式
(2)由定义可知 P、Q 的中点一定在超平面上
(3)移项后就得到了超平面的偏移量
w x + b = 0 ( 1 ) w P + Q 2 + b = 0 ( 2 ) b = − P + Q 2 w ( 3 ) \begin{aligned} & wx + b = 0 & (1) \\ & w\frac{P + Q}{2} + b = 0 & (2) \\ & b = -\frac{P + Q}{2}w & (3) \\ \end{aligned} wx+b=0w2P+Q+b=0b=−2P+Qw(1)(2)(3)
即得证
五、代码实现
使用 Python 实现:
import numpy as np
from queue import PriorityQueue
def means(X):
"""
启发式的选取两个点
参数
----------
X : 特征矩阵
返回
----------
两个向量点
"""
iteration_steps = 20
count = X.shape[0]
i = np.random.randint(0, count)
j = np.random.randint(0, count - 1)
# 保证 i\j 不相同
j += (j >= i)
ic = 1
jc = 1
p = X[i]
q = X[j]
for l in range(iteration_steps):
k = np.random.randint(0, count)
di = ic * distance(p, X[k])
dj = jc * distance(q, X[k])
if di == dj:
continue
if di < dj:
p = (p * ic + X[k]) / (ic + 1)
ic = ic + 1
else:
q = (q * jc + X[k]) / (jc + 1)
jc = jc + 1
return p, q
def distance(a, b):
"""
计算距离
参数
----------
a : 向量 a
b : 向量 b
返回
----------
向量 a 与 向量 b 直接的距离
"""
return np.linalg.norm(a - b)
class annoynode:
"""
Annoy 树结点
"""
def __init__(self, index, size, w, b, left = None, right = None):
# 结点包含的样本点下标
self.index = index
# 结点及其子结点包含的样本数
self.size = size
# 分割超平面的系数
self.w = w
# 分割超平面的偏移量
self.b = b
# 左子树
self.left = left
# 右子树
self.right = right
def __lt__(self, other):
# 结点大小比较
return self.size < other.size
class annoytree:
"""
Annoy 树算法实现
参数
----------
X : 特征矩阵
leaf_size : 叶子节点包含的最大特征向量数量,默认为 10
"""
def __init__(self, X, leaf_size = 10):
def build_node(X_indexes):
"""
构建结点
参数
----------
X_indexes : 特征矩阵下标
"""
# 当特征矩阵小于等于指定的叶子结点的大小时,创建叶子结点并返回
if len(X_indexes) <= leaf_size:
return annoynode(X_indexes, len(X_indexes), None, None)
# 当前特征矩阵
_X = X[X_indexes, :]
# 启发式的选取两点
p, q = means(_X)
# 超平面的系数
w = p - q
# 超平面的偏移量
b = -np.dot((p + q) / 2, w)
# 构建结点
node = annoynode(None, len(X_indexes), w, b)
# 在超平面“左”侧的特征矩阵下标
left_index = (_X.dot(w) + b) > 0
if left_index.any():
# 递归的构建左子树
node.left = build_node(X_indexes[left_index])
# 在超平面“右”侧的特征矩阵下标
right_index = ~left_index
if right_index.any():
# 递归的构建右子树
node.right = build_node(X_indexes[right_index])
return node
# 根结点
self.root = build_node(np.array(range(X.shape[0])))
class annoytrees:
"""
Annoy 算法实现
参数
----------
X : 特征矩阵
n_trees : Annoy 树的数量,默认为 10
leaf_size : 叶子节点包含的最大特征向量数量,默认为 10
"""
def __init__(self, X, n_trees = 10, leaf_size = 10):
self._X = X
self._trees = []
# 循环的创建 Annoy 树
for i in range(n_trees):
self._trees.append(annoytree(X, leaf_size = leaf_size))
def query(self, x, k = 1, search_k = -1):
"""
查询距离最近 k 个特征向量
参数
----------
x : 目标向量
k : 查询邻居数量
search_k : 最少遍历出的邻居数量,默认为 Annoy 树的数量 * 查询数量
"""
# 创建结点优先级队列
nodes = PriorityQueue()
# 先将所有根结点加入到队列中
for tree in self._trees:
nodes.put([float("inf"), tree.root])
if search_k == -1:
search_k = len(self._trees) * k
# 待查询的邻居下标数组
nns = []
# 循环优先级队列
while len(nns) < search_k and not nodes.empty():
# 获取优先级最高的结点
(dist, node) = nodes.get()
# 如果是叶子结点,将下标数组加入待查询的邻居中
if node.left is None and node.right is None:
nns.extend(node.index)
else:
# 计算目标向量到结点超平面的距离
dist = min(dist, np.abs(x.dot(node.w) + node.b))
# 将距离做为优先级的结点加入到优先级队列中
if node.left is not None:
nodes.put([dist, node.left])
if node.right is not None:
nodes.put([dist, node.right])
# 对下标数组进行排序
nns.sort()
prev = -1
# 优先级队列
nns_distance = PriorityQueue()
for idx in nns:
# 过滤重复的特征矩阵下标
if idx == prev:
continue
prev = idx
# 计算特征向量与目标向量的距离做为优先级
nns_distance.put([distance(x, self._X[idx]), idx])
nearests = []
distances = []
# 取前 k 个
for i in range(k):
if nns_distance.empty():
break
(dist, idx) = nns_distance.get()
nearests.append(idx)
distances.append(dist)
return nearests, distances
六、第三方库实现
Annoy2 实现:
from annoy import AnnoyIndex
# 初始化 AnnoyIndex,使用欧式距离
t = AnnoyIndex(d, 'euclidean')
for i in range(100):
# 添加样本点
t.add_item(i, trains[i])
# 构建 10 棵二叉树
t.build(10)
# 查询 test 点最近 5 个样本点
t.get_nns_by_vector(test, 5, include_distances=True)
七、示例演示
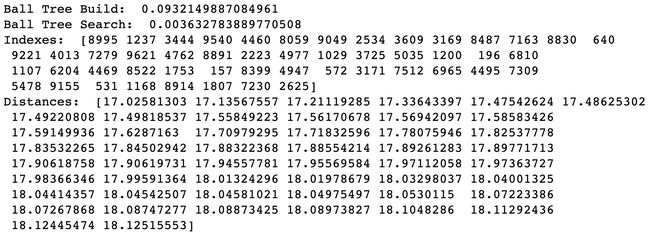
下图 6-1、6-2 分别展示了在 10000 个 200 维的特征矩阵下,使用 Annoy 算法和 BallTree 算法进行构建与查询的结果。可以看到 Annoy 的构建时间是 BallTree 的 2 倍左右,查询时间快了近 10 倍,但是 Annoy 没有找到最近邻,而是找到了附近的其他的特征向量,这也是 ANN 的特性,拿搜索的精度换查询速度。
当然 Annoy 可以增减搜索的范围或者改变树的数量来平衡搜索精度与查询速度,这个需要根据业务需求进行动态的调整。
八、思维导图
九、参考文献
- https://en.wikipedia.org/wiki/Nearest_neighbor_search#Approximate_nearest_neighbor
- https://github.com/spotify/annoy
- https://erikbern.com/2015/10/01/nearest-neighbors-and-vector-models-part-2-how-to-search-in-high-dimensional-spaces.html
完整演示请点击这里
注:本文力求准确并通俗易懂,但由于笔者也是初学者,水平有限,如文中存在错误或遗漏之处,恳请读者通过留言的方式批评指正
本文首发于——AI导图,欢迎关注