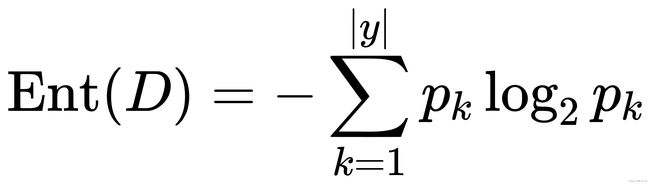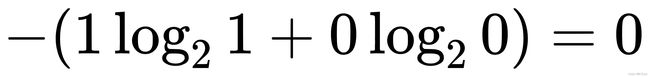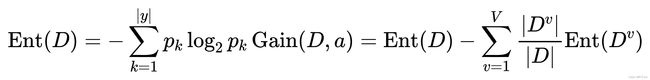机器学习--决策树

目录

基本概念

什么是决策树

信息熵

信息增益

 决策树的剪枝

决策树实现

代码实现

---

基本概念

什么是决策树

决策树（Decision Tree）是一种基本的分类与回归方法，它是一种监督学习，决策树模型呈树形结构，是逻辑上的if-than，每一个分支就是一个推导过程，每一个叶节点是一个类别。

信息熵

决策树算法的关键在于如何选择最优划分属性。一般而言，我们希望决策树的分支节点所包含的样本尽可能属于同一类别，即其纯度越高越好。衡量纯度标准常用信息熵，计算公式如下：

其中|y|表示有几类，pk表示第k类样本的占比。

信息熵值越小，纯度则越高。

举例计算：

红绿球信息熵计算

Id	R	G
1	4	0
2	3	1
3	2	2

第一次P(R)=1,P(G=0，信息熵为：

 第二次P(R)=3/4,P(G)=1/4，信息熵为：

第三次P(R)=P(G)=1/2,信息熵为：

信息增益

如果单纯的用信息熵去划分决策树的分支可能会导致决策树的分支太多太复杂，引入了信息增益，是一个统计量，用来描述一个属性区分数据样本的能力。信息增益越大，那么决策树就会越简洁。这里信息增益的程度用信息熵的变化程度来衡量，信息增益越大，表示变量消除不确定性的能力越强。公式如下。

距离计算

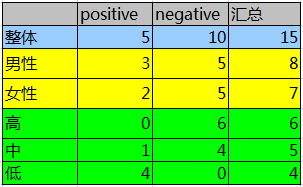
第二列为性别，第三列为活跃度，最后一列用户是否流失。 

计算性别对用户流失的影响：

首先计算整体熵：

计算性别熵 

 最后就可以计算性别信息增益

 决策树的剪枝

是否会有这样一种情况：决策树的一条分支上的样例太少，比如西瓜分类决策树的一个分支是这样的，根蒂蜷缩的是坏瓜仅有一个样例，然后把他分类为坏瓜。但实际上有可能根蒂蜷缩的大部分都是好瓜。这将会导致过拟合，因此我们需要采取剪枝策略。

剪枝分为预剪枝和后剪枝。

• 预剪枝：在构建决策树的过程中，提前终止决策树的生长，从而避免过多节点的产生。但是预剪枝过于简单，实用性不强，而且无法知道剪枝的精确节点。
• 后剪枝：在决策树建成后，对数据置信度不达标的数据节点子树用叶子节点进行代替，该叶子节点的类标号用该节点子树中频率最高的类标记。而后剪枝又分为两种：

1. 把训练数据集分成树的生长集和剪枝集
2. 使用同一数据集进行决策树生长和剪枝。

决策树实现

上次KNN算法的数据是距离不好做分类。这次决策树用到的数据集简单的模拟信用卡的办理。

数据集分四个属性（age,income,student,credit_rating）

数据集

age	income	student	credit_rating	label
0	2	0	0	N
0	2	0	1	N
1	2	0	0	Y
2	1	0	0	Y
2	0	1	0	Y
2	0	1	1	N
1	0	1	1	Y
0	1	0	0	N
0	0	1	0	Y
2	1	1	0	Y
0	1	1	1	Y
1	1	0	1	Y
1	2	1	0	Y
2	1	0	1	N

测试集

age	income	student	credit_rating
0	1	0	0
0	2	1	0
2	1	1	0
0	1	1	1
1	1	0	1
1	0	1	0
2	1	0	1

代码实现

import numpy as np

import pickle
import os
import treePlotter

# 创建训练数据
def CreateTrainingDataset():
    X = [[0, 2, 0, 0, 'N'],
         [0, 2, 0, 1, 'N'],
         [1, 2, 0, 0, 'Y'],
         [2, 1, 0, 0, 'Y'],
         [2, 0, 1, 0, 'Y'],
         [2, 0, 1, 1, 'N'],
         [1, 0, 1, 1, 'Y'],
         [0, 1, 0, 0, 'N'],
         [0, 0, 1, 0, 'Y'],
         [2, 1, 1, 0, 'Y'],
         [0, 1, 1, 1, 'Y'],
         [1, 1, 0, 1, 'Y'],
         [1, 2, 1, 0, 'Y'],
         [2, 1, 0, 1, 'N']]
    attributeList = ["age", "income", "student", "credit_rating"]
    return X, attributeList

# 创建测试数据
def CreateTestDataset():
    X = [[0, 1, 0, 0],
         [0, 2, 1, 0],
         [2, 1, 1, 0],
         [0, 1, 1, 1],
         [1, 1, 0, 1],
         [1, 0, 1, 0],
         [2, 1, 0, 1]]

    attributeList = ["age", "income", "student", "credit_rating"]
    return X, attributeList

# 计算类别的统计信息
def GetClassInfo(Dataset):
    classInfo = {}
    for item in Dataset:
        if item[-1] not in classInfo.keys():
            classInfo[item[-1]] = 1
        else:
            classInfo[item[-1]] += 1
    classInfo = dict(sorted(classInfo.items(), key=lambda x: x[1], reverse=True))

    return classInfo

# 计算最大占比类
def CalMostClass(classInfo):
    maxClass = list(classInfo.keys())[0]
    return maxClass

# 计算数据集的信息熵
def ComputeEntropy(Dataset):
    ClassInfo = GetClassInfo(Dataset)
    entropy = 0
    amount = 0
    p = []  # p[]存放的是第k个类的数据个数

    for _, val in ClassInfo.items():
        p.append(val)
        amount += val
    for pk in p:
        entropy -= (pk / amount) * np.log2(pk / amount)

    return entropy

# 计算数据集在某个属性上的的信息增益Gain(attributeList)
# Gain(D, a)
def computeAttrGainNPartition(Dataset, attributeIndex):
    gain = ComputeEntropy(Dataset)  # Initialize：初始化等于数据集D的信息熵

    # 按属性的值划分数据集子集
    LEN_DATASET = len(Dataset)
    # attributePartition = {"attrVal1": [[], [] ,.., []], ..., "attrValn": [[], [] ,.., []]}
    attributePartition = {}
    for dataItem in Dataset:
        if dataItem[attributeIndex] not in attributePartition.keys():
            attributePartition[dataItem[attributeIndex]] = []
            attributePartition[dataItem[attributeIndex]].append(dataItem)
        else:
            attributePartition[dataItem[attributeIndex]].append(dataItem)

    amount = 0
    lenth = []
    Ent = []

    # 计算信息增益
    for key, valDataSet in attributePartition.items():
        Ent.append(ComputeEntropy(valDataSet))
        lenth.append(len(valDataSet))
        amount += len(valDataSet)
    for i in range(len(Ent)):
        gain -= (lenth[i] / LEN_DATASET) * Ent[i]

    return gain, attributePartition

# 建决策树
def CreateDecisionTree(Dataset, attributeList):
    attrList = attributeList
    Tree = {}
    classInfo = GetClassInfo(Dataset)
    LEN_DATASET = len(Dataset)

    # 建立叶子节点情况1：给定的属性集为空 ---- 不能划分
    if len(attributeList) == 0:
        return CalMostClass(classInfo)

    # 建立叶子节点情况2：给定的数据集所有label都相同 ---- 无需划分
    for key, valLen in classInfo.items():
        if valLen == LEN_DATASET:
            return key
        break

    # 建立叶子节点情况3：样本在属性集上取值都相等 ---- 无法划分
    temp = Dataset[0][:-1]
    sameCnt = 0
    for dataItem in Dataset:
        if temp == dataItem[:-1]:
            sameCnt += 1
    if sameCnt == LEN_DATASET:
        return CalMostClass(classInfo)

    # 选择最佳划分属性
    theBestAttrIndex = 0
    theBestAttrGain = 0
    theBestAttrPartition = {}

    for attributeIndex in range(len(attributeList)):
        gain, attributePartition = computeAttrGainNPartition(Dataset, attributeIndex)

        if gain > theBestAttrGain:
            theBestAttrGain = gain
            theBestAttrIndex = attributeIndex
            theBestAttrPartition = attributePartition

    attrName = attributeList[theBestAttrIndex]
    # python的list对象按索引删除对象，使用的是del()函数
    del (attributeList[theBestAttrIndex])

    # # 为了方便后面建子树，将此时的attr对应的那列去除
    for key, valList in theBestAttrPartition.items():
        for index in range(len(valList)):
            temp = valList[index][:theBestAttrIndex]
            temp.extend(valList[index][theBestAttrIndex + 1:])
            valList[index] = temp


    # 根据属性的值，建立分叉节点
    Tree[attrName] = {}

    for keyAttrVal, valDataset in theBestAttrPartition.items():
        # 因为python对iterable list对象的传参是按地址传参，会改变attributeList的值
        # 所以在传attributeList参数的时候，创建一个副本，就相当于按值传递了
        subLabels = attributeList[:]
        # valDataset是已去除attr的data，attributeList是已去除attr的attributeList
        Tree[attrName][keyAttrVal] = CreateDecisionTree(valDataset, subLabels)

    return Tree

# 测试做分类
def Predict(DataSet, testArrtList, decisionTree):
    predicted_label = []

    for dataItem in DataSet:
        cur_decisionTree = decisionTree
        # 如果root就是叶子结点leaf
        if type(cur_decisionTree) == set:   # 例如：{'N'}
            node = list(cur_decisionTree)
        else:
            node = list(cur_decisionTree.keys())[0]
            # 只要temp处在attributeList，说明当前处在树枝结点(非叶子)上, 否则处在叶子结点
        while node in testArrtList:
            cur_index = testArrtList.index(node)  # 0 2
            cur_element = dataItem[cur_index]  # 0 0
            cur_decisionTree = cur_decisionTree[node][cur_element]  # {'student': {0: 'N', 1: 'Y'}} N
            if type(cur_decisionTree) == dict:
                node = list(cur_decisionTree.keys())[0]  # student
            else:
                node = cur_decisionTree
        predicted_label.append(node)
    return predicted_label

# 将模型保存起来
def SaveModel(decisionTree, filename):
    # 由于pickle是将文本序列化成binary文件，故需用wb
    f = open(filename, 'wb')
    pickle.dump(decisionTree, f)

# 读取模型
def LoadModel(filename):
    # 由于pickle读取的是binary文件，故需用rb
    f = open(filename, 'rb')
    return pickle.load(f)

if __name__ == '__main__':
    base = os.path.dirname(os.path.abspath(__file__))
    trainingDataset, attributeList = CreateTrainingDataset()
    testDataset, testArrtList = CreateTestDataset()

    path = base + "DecisionTreeModel.txt"
    # 建决策树
    decisionTree = CreateDecisionTree(trainingDataset, attributeList)
    # 保存模型
    SaveModel(decisionTree, path)
    # 读取模型
    model = LoadModel(path)
    print(model)
    # 对测试数据进行预测label
    result = Predict(testDataset, testArrtList ,model)
    print(result)

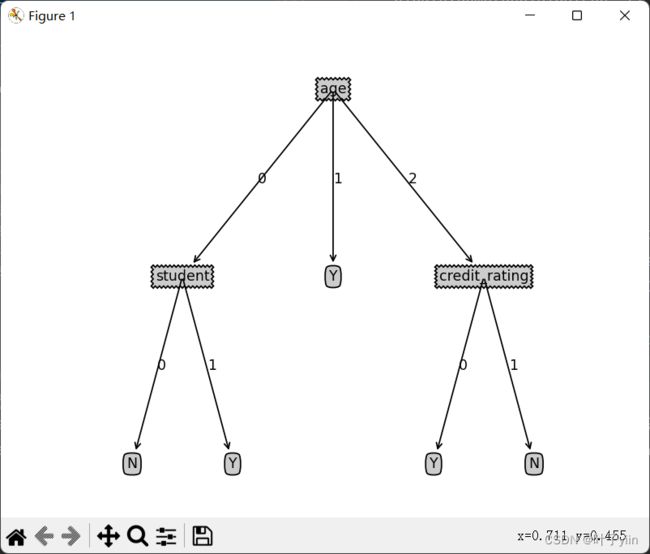
    treePlotter.createPlot(model)

树的可视化结果