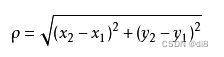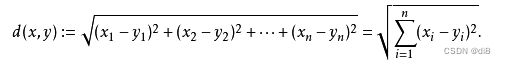knn算法

k近邻算法的概述
工作机制：给定测试样本，基于某种距离度量找出训练集中与其最靠近的k个训练样本，然后基于这k个“邻居”的信息来进行预测。通常，在分类任务中可使用“投票法”，即选择这k个样本中出现最多的类别标记作为预测结果；在回归任务中可使用“平均法”，即将这k个样本的实值输出标记的平均值作为预测结果；还可基于距离远近进行加权平均或加权投票，距离越近的样本权重越大。

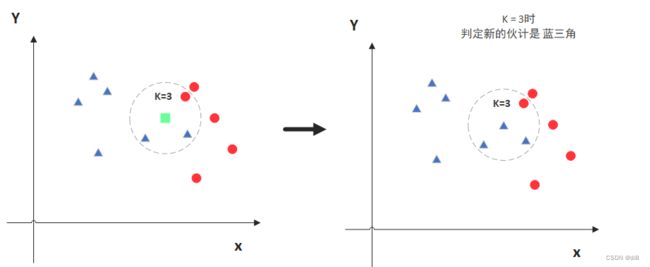
图中绿色的点就是要预测的那个点，假设K=3。那么KNN算法就会找到与它距离最近的三个点（这里用圆圈把它圈起来了），看看哪种类别多一些，比如这个例子中是蓝色三角形多一些，新来的绿色点就归类到蓝三角了。

但是，当K=5的时候，判定就变成不一样了

k-近邻算法一般流程

1.计算已知类别数据集中的点与当前点之间的距离；

2.按照距离递增次序排序；

3.选取与当前点距离最小的k个点；

4.确定前k个点所在类别的出现频率；

5.返回前k个点出现频率最高的类别作为当前点的预测分类

距离计算

要度量空间中点距离的话，有好几种度量方式，比如常见的曼哈顿距离计算，欧式距离计算等等。不过通常KNN算法中使用的是欧式距离，以二维平面为例，，二维空间两个点的欧式距离计算公式如下：

 拓展到多维空间，则公式变成这样:

K值选择

从选取一个较小的K值开始，不断增加K的值，然后计算验证集合的方差，最终找到一个比较合适的K值。

关于交叉验证：将样本数据按照一定比例，拆分出训练用的数据和验证用的数据，比如6：4拆分出部分训练数据和验证数据。

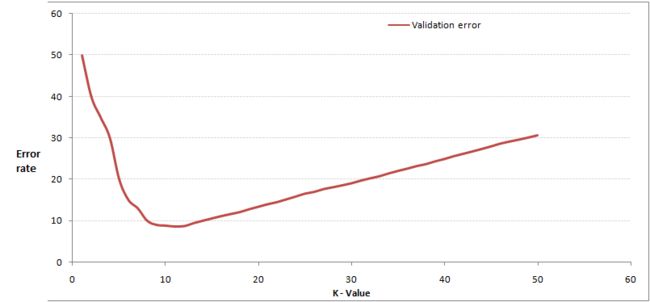
通过交叉验证计算方差后得到下面这样的图：

 随着k的不断增加，错误率会先降低，因为周围有更多的样本可以借鉴，分类效果会变好。但当K值更大的时候，错误率会更高。这也很好理解，假设一共有35个样本，当K增大到30的时候，KNN基本上就没意义了。

KNN算法的优势和劣势

了解KNN算法的优势和劣势，可以帮助我们在选择学习算法的时候做出更加明智的决定。那我们就来看看KNN算法都有哪些优势以及其缺陷所在！

KNN算法优点

1. 简单易用，相比其他算法，KNN算是比较简洁明了的算法。即使没有很高的数学基础也能搞清楚它的原理。
2. 模型训练时间快，上面说到KNN算法是惰性的，这里也就不再过多讲述。
3. 预测效果好。
4. 对异常值不敏感

KNN算法缺点

1. 对内存要求较高，因为该算法存储了所有训练数据
2. 预测阶段可能很慢
3. 对不相关的功能和数据规模敏感

knn算法实例

代码实现（以鸢尾花类型判别为例）

鸢尾花数据集地址：UCI Machine Learning Repository: Iris Data Sethttps://archive.ics.uci.edu/ml/datasets/Iris

 数据集划分

def create_data():
    #导入数据
    path="D:\data\iris.data"
    df=pd.read_csv(path)
    np_tests=np.array(df)
    #分割数据集与测试集，数据集占70%，测试集占30%
    train = np_tests[:int(len(np_tests) * 0.7)]
    test = np_tests[int(len(np_tests) * 0.7):]
    #分别将数据集的数据与标签赋值给两个不同的变量
    x_train = train[:,0:4]
    y_train = train[:,-1]
    #分别将测试集的数据与标签赋值给两个不同的变量
    x_test = test[:,0:4]
    y_test = test[:,-1]
    return x_train,y_train,x_test,y_test

（数据集大致长这样，前四个为属性，最后为鸢尾花类别）

 误差函数

def error_rate(a):
    x=0
    y=0
    for i in a:
        if i=='true':
            x+=1
        else:
            y+=1
    error=y/(x+y)
    return round(error,2) 

 knn算法

#计算目标点到样本点的距离（这里采用欧式距离计算公式）
def calculate_dis(x_train, x_test1, k = 3):
     dis = (x_train - x_test1)**2
     dis = dis.sum(axis = 1)**0.5
     dis = dis.argsort()  # 距离值以从小到大排序，将对应索引赋给dis
     small_k = dis[:k]  #将dis前k个值取出，即k个离目标点最近的点
     return dis,small_k

# 确定预测点所属类别
def pre_result(small_k, y_train):
    dic = {}  #定义一个字典，用来保存不同标签值对应的样本数量
    for i in small_k:
        if y_train[i] in dic.keys(): #dic.keys()是保存键（标签）的序列
            dic[y_train[i]] += 1 
        else:
            dic[y_train[i]] = 1   #没出现过的标签赋值为1
    c=sorted(dic.items(), key=lambda x: x[1],reverse=True)#将字典的键对应的值从大到小排列
    b=c[0]  #取出值最大（标签数最多）的键值对
    return b[0] #返回标签数最多的键

整体代码

#导包
import numpy as np;
import pandas as pd;
from sklearn.preprocessing import MinMaxScaler
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt

def create_data():
    #导入数据
    path="D:\data\iris.data"
    df=pd.read_csv(path)
    np_tests=np.array(df)
    #分割数据集与测试集，数据集占70%，测试集占30%
    train = np_tests[:int(len(np_tests) * 0.7)]
    test = np_tests[int(len(np_tests) * 0.7):]
    #分别将数据集的数据与标签赋值给两个不同的变量
    x_train = train[:,0:4]
    y_train = train[:,-1]
    #分别将测试集的数据与标签赋值给两个不同的变量
    x_test = test[:,0:4]
    y_test = test[:,-1]
    return x_train,y_train,x_test,y_test


#计算目标点到样本点的距离（这里采用欧式距离计算公式）
def calculate_dis(x_train, x_test1, k):
     dis = (x_train - x_test1)**2
     dis = dis.sum(axis = 1)**0.5
     dis = dis.argsort()  # 距离值以从小到大排序，将对应索引赋给dis
     small_k = dis[:k]  #将dis前k个值取出，即k个离目标点最近的点
     return dis,small_k

# 确定预测点所属类别
def pre_result(small_k, y_train):
    dic = {}  #定义一个字典，用来保存不同标签值对应的样本数量
    for i in small_k:
        if y_train[i] in dic.keys(): #dic.keys()是保存键（标签）的序列
            dic[y_train[i]] += 1 
        else:
            dic[y_train[i]] = 1   #没出现过的标签赋值为1
    c=sorted(dic.items(), key=lambda x: x[1],reverse=True)#将字典的键对应的值从大到小排列
    b=c[0]  #取出值最大（标签数最多）的键值对
    return b[0] #返回标签数最多的键

# 误差函数
def error_rate(a):
    x=0
    y=0
    for i in a:
        if i=='true':
            x+=1
        else:
            y+=1
    error=y/(x+y)
    return round(error,2)

 #可视化
def show(error_list):
  plt.figure(figsize=(6, 3), dpi=100)
  k =[3,4,5,6,7,8,9,10,11,12]
  error_rate = error_list
  plt.plot(k, error_rate)
  plt.show()
   
def main():
    x_train, y_train,x_test,y_test= create_data()
    error_list=[] #定义一个数组，存放错误率

    for k in [3,4,5,6,7,8,9,10,11,12]:
       array=[] #存放true和false值的数组
       j=0

       for i in x_test:  #测试集测试
         dis, small_k = calculate_dis(x_train,i,k)
         pre = pre_result(small_k, y_train)
         if pre == y_test[j]: #将测试结果与真实值作比较
             array.append('true')
             j+=1
         else:
             array.append('false')
             j+=1
       error=error_rate(array) #代入误差函数求取错误率
       error_list.append(error) #将错误率存入该数组
       
    print(error_list)
    show(error_list) 

if __name__ == '__main__':
    main()

array(测试结果序列）

错误率可视化

 

错误率

通过实验发现，随着k值的增大误差也在逐渐增大。

总结：通过knn算法，可以实现基本的分类问题。k值较大，比较稳定，但过于平滑。k值较小，分类结果容易受噪声影响，出现过拟合。由于数据较少，在计算错误率时发现，无法更加细致地算出错误率的多少，对k值的判断不够准确。