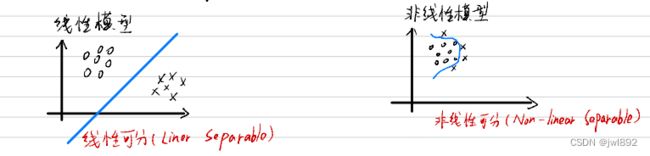支持向量机(Support Vector Machine)
支持向量机(Support Vector Machine)
SVM是最大化间隔（Margin）的分类算法。
在此之前，我们先说两个机器学习中常见的定理：
1.No Free Lunch Theorem：
如果我们不对特征空间有先验假设，则所有算法的平均表现是一样的。
2.我们认为：特征差距小的样本更有可能是同一类。
一、线性模型
1.定义
如果存在一条直线，可以划分两个样本集，则必然存在无数条直线，那么哪条直线式最好的？
如下图，三条直线哪条线式最好的？为什么？
我们可以从不同的方面来讨论一下：
（1）所有的特征向量最后的影响差不多：
①对x轴对应的特征进行划分，最好的一条线是L2；
②对y轴对应的特征进行划分，最好的一条线是L1。
（2）对错误的容忍程度大小，最好的是L3。（因为左上角的点下移，右下角的点上移，都会造成误差，如下图）
（3）定义一个性能指标（每条线都有的性能指标），此时L3能算到最大。为什么？
证明：
随便形成一个能划分两个数据集的线（此时不必为最优线），这条线往左侧移动，直到碰到第一个（或同时几个）O点为止，同样，这条线向右移动，碰到第一个（或同时几个）X点为止 ，这两条绿线之间的距离为 d d d（margin)，然后不断反复尝试，寻找指标 d d d最大的两条绿线，这两条绿线之间 d 2 \frac{d}{2} 2d的位置的那条线就是我么寻找的最优的那条线。被两条绿线插到的向量叫支持向量（support vectors）。
1.2数学描述
1.首先我们定义：
（1）训练数据及标签
( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x n , y n ) (x_1,y_1),(x_2,y_2),\cdots,(x_n,y_n) (x1,y1),(x2,y2),⋯,(xn,yn)
其中 x 1 x_1 x1为向量， y 1 y_1 y1为标签。在上面证明里的图中， x 1 x_1 x1为二维向量， y i = { + 1 − 1 y_i=\begin{cases}+1 \\ -1 \end{cases} yi={+1−1。
（2）线性模型参数： ( ω , b ) (\omega,b) (ω,b)
ω ⊤ x + b = 0 （ 超 平 面 − H y p e r p l a n e ） \omega^{\top} x+b=0 \qquad （超平面-Hyperplane） ω⊤x+b=0（超平面−Hyperplane）
ω \omega ω为一个维度与 x x x一样的向量， b b b为常数。
要做的事：用方程限定一个模型，用训练样本和算法算出 ω \omega ω和 b b b。
（3）线性可分：一个训练集 { ( x i , y i ) } i = 1 N \left \{(x_i,y_i) \right \} _{i=1}^N {(xi,yi)}i=1N线性可分是指存在 ( ω , b ) (\omega,b) (ω,b)，使对任意i=1~N，有：
①若 y i = + 1 y_i=+1 yi=+1，则 ω ⊤ x + b ≥ 0 \omega^{\top} x+b \ge 0 ω⊤x+b≥0；
②若 y i = − 1 y_i=-1 yi=−1，则 ω ⊤ x + b < 0 \omega^{\top} x+b < 0 ω⊤x+b<0。
即
y i [ ω ⊤ x + b ] ≥ 0 ⋯ 公 式 ( 1 ) y_i[\omega^{\top} x+b] \ge 0 \qquad \qquad \cdots公式(1) yi[ω⊤x+b]≥0⋯公式(1)
2.优化问题（二次规划问题）
m i n 1 2 ∥ ω ∥ 2 s . t . y i [ ω ⊤ x i + b ] ≥ 1 min\frac{1}{2}\left \| \omega \right \|^2 \\ s.t. \quad y_i[\omega^{\top} x_i+b] \ge 1 min21∥ω∥2s.t.yi[ω⊤xi+b]≥1
为什么这里变成了 y i [ ω ⊤ x + b ] ≥ 1 y_i[\omega^{\top} x+b] \ge 1 yi[ω⊤x+b]≥1了呢？为什么要最小化 ω \omega ω呢？这里是我认为在这个知识点里比较难理解的部分，下面进行一些解释：
事实1： ω ⊤ x + b = 0 \omega^{\top} x+b=0 ω⊤x+b=0与 a ω ⊤ x + a b = 0 a\omega^{\top} x+ab=0 aω⊤x+ab=0是同一平面（ a ∈ R + a\in R^+ a∈R+）。
若 ( ω , b ) (\omega,b) (ω,b)满足公式（1），则 ( a ω , a b ) (a\omega,ab) (aω,ab)也满足公式（1）。
事实2：点到平面的距离公式：假设平面 ω 1 x + ω 2 y + b = 0 \omega_1x+\omega_2y+b=0 ω1x+ω2y+b=0， ( x 0 , y 0 ) (x_0,y_0) (x0,y0)到此平面的距离：
d = ∣ ω 1 x 0 + ω 2 y 0 + b ∣ ω 1 2 + ω 2 2 d=\frac{\left | \omega_1x_0+\omega_2y_0+b\right | }{\sqrt {\omega_1^2+\omega_2^2}} d=ω12+ω22∣ω1x0+ω2y0+b∣
向量 x o x_o xo到超平面 ω ⊤ x + b = 0 \omega^{\top} x+b=0 ω⊤x+b=0的距离：
d = ∣ ω ⊤ x 0 + b ∣ ∥ ω ∥ d=\frac{\left | \omega^{\top} x_0+b\right | }{\left \| \omega \right \|}\\ d=∥ω∥∣∣ω⊤x0+b∣∣
其中 ∥ ω ∥ = ω 1 2 + ω 2 2 + ⋯ + ω n 2 \left \| \omega \right \|=\sqrt{\omega_1^2+\omega_2^2+\cdots+\omega_n^2} ∥ω∥=ω12+ω22+⋯+ωn2。
我们可以用 a a a去缩放 ( ω , b ) → ( a ω , a b ) (\omega,b)\to (a\omega,ab) (ω,b)→(aω,ab)，最终使在支持向量 x 0 x_0 x0上，有
∣ ω ⊤ x 0 + b ∣ = 1 \left | \omega^{\top} x_0+b\right |=1 ∣∣ω⊤x0+b∣∣=1
此时，支持向量与平面的距离为
d = 1 ∥ ω ∥ d=\frac{1 }{\left \| \omega \right \|}\\ d=∥ω∥1
不是支持向量的点必然 ∣ ω ⊤ x 0 + b ∣ > 1 \left | \omega^{\top} x_0+b\right |>1 ∣∣ω⊤x0+b∣∣>1，由于点存在正负，综合出来就是
y i [ ω ⊤ x + b ] ≥ 1 y_i[\omega^{\top} x+b] \ge 1 yi[ω⊤x+b]≥1
解释完毕。
顺便说一下二次规划（Quadratic pragramming），它使属于凸优化里的一种，需要满足以下条件：
①目标函数使二次项；
②限制条件是一次项。
二次规划要么无解，要么只有一个极值。
二、非线性模型
如果样本集不是线性可分的，那么我们就不能像上面的处理方式一样求出 ω \omega ω和 b b b。
处理非线性：
1.最小化：
m i n 1 2 ∥ ω ∥ 2 + C Σ i = 1 N σ i s . t . y i [ ω ⊤ x i + b ] ≥ 1 − σ i σ i ≥ 0 min\frac{1}{2} \left \| \omega \right \|^2+C\Sigma_{i=1}^N \sigma _i \\ s.t. \quad y_i[\omega^{\top} x_i+b] \ge 1-\sigma _i\\ \sigma _i\ge 0 min21∥ω∥2+CΣi=1Nσis.t.yi[ω⊤xi+b]≥1−σiσi≥0
其中， σ i \sigma _i σi为松弛变量（Slack variable），C为事先设定的参数，i=1~N。此时， y i y_i yi和 x i x_i xi是已知的， ω \omega ω, b b b, σ i \sigma _i σi是未知的。