数据结构学习笔记(7.查找 8.排序)
文章目录
- 第七章 查找
-
- 查找--基本概念
- 顺序查找
- 折半查找(二分法查找)--重要考点
- 分块查找
- 二叉排序树BST
- 平衡二叉树--AVL--重要考点
- 平衡二叉树的删除操作
- 红黑树--RBT
- 红黑树的插入
- 红黑树--删除操作
- B树
- B树的插入和删除
- B+树
- 散列查找
- 第八章 排序
-
- 排序--基本概念
- 插入排序
- 希尔排序
- 冒泡排序
- 快速排序
- 简单选择排序
- 堆排序
- 堆--插入和删除
- 归并排序
- 基数排序
- 外部排序
- 败者树
- 置换--选择排序
- 最佳归并树
第七章 查找
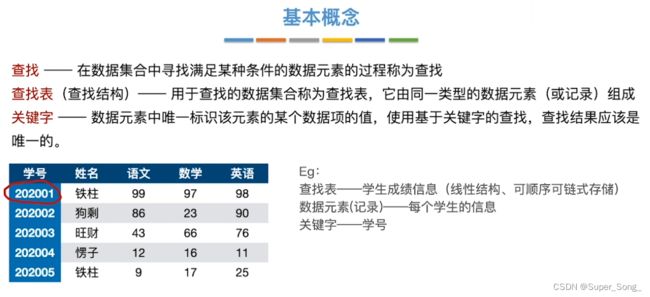
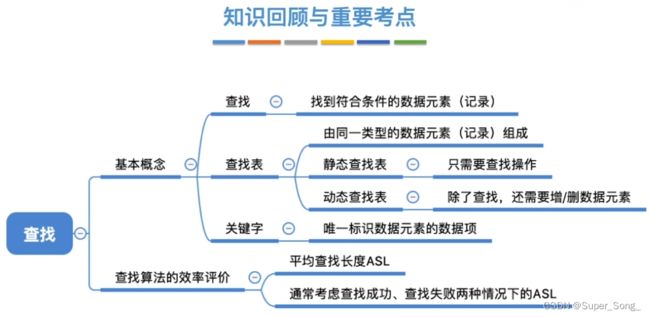
查找–基本概念
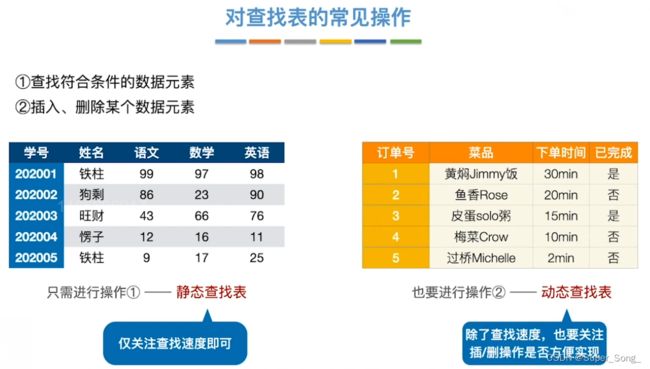
- 只查找,静态查找表
- 插入,删除,动态查找
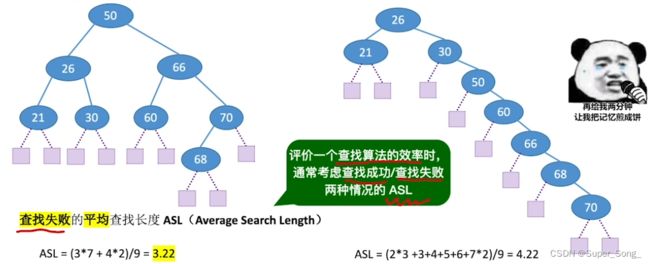
- 查找长度,平均查找长度,默认查找任何一个元素的概率相等
- asl的数量级,反映了查找算法时间复杂度
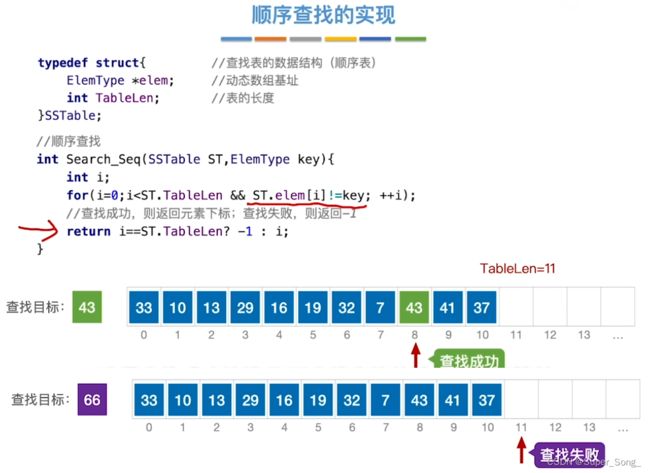
顺序查找
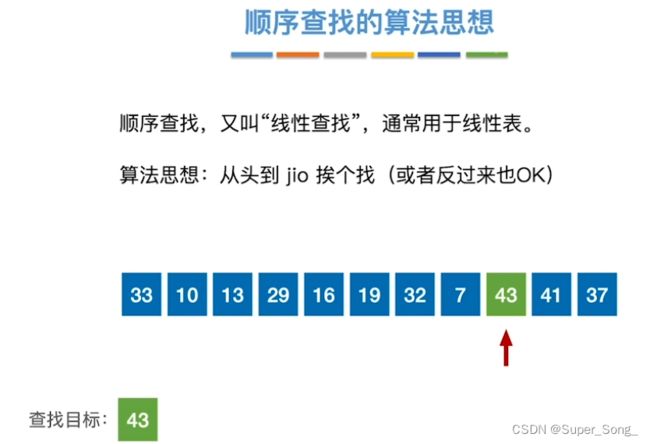
- 不论顺序表还是链表,都是从头到脚向后查
- 增加了哨兵,用来保存要查找的元素
- 从后向前查找,如果一直到0号位,才相同,说明没有查到
- 效率略有提高,但不明显,因为循环到0号位自动结束,不需要长度的判断
- 成功还是失败,时间复杂度都是O(n)
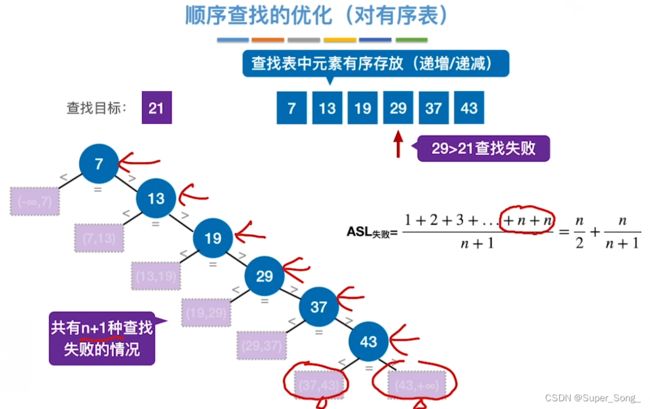
- 如果查找表原本就是有序的
- 查找21,结果发现到了29还没有,说明就已经查找失败了
- n个元素,有n+1中失败的情况
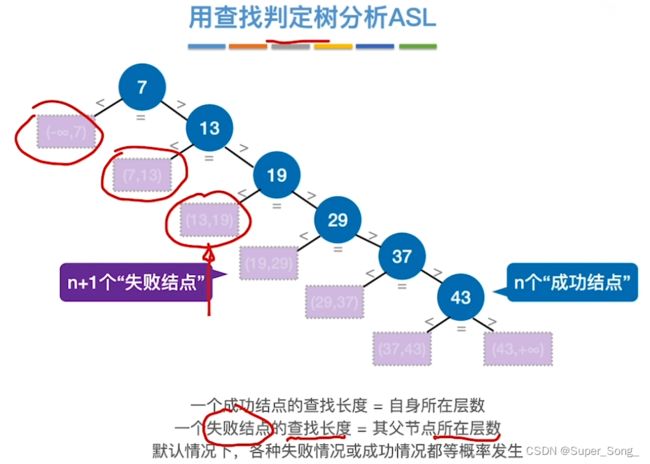
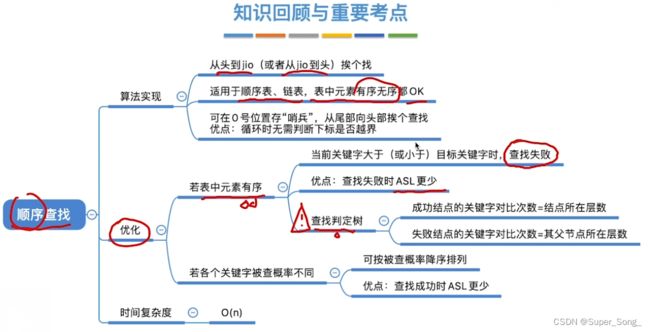
- 成功结点的查找长度=自身所在层数,比如查19,19在3层,查找长度就是3
- 失败结点的查找长度=父节点所在层数,比如查找的数在(13,19)区间,其父节点就是19,19在3层,查找长度就是3
- 要学会画查找判定树,利用查找判定树来分析查找效率
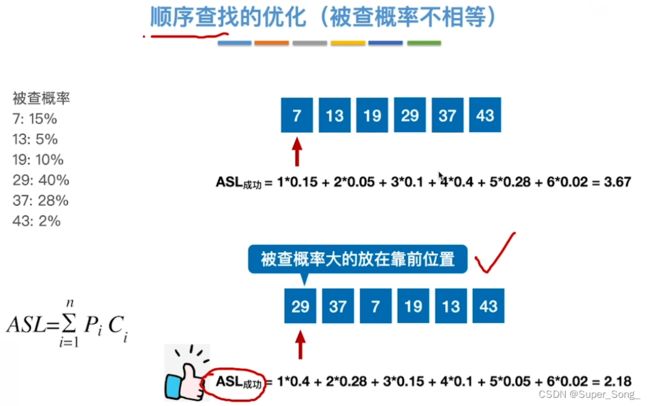
- 可以将被查概率大的元素放在靠前的位置
- 对于查找成功来说,降低了平均查找长度
- 但是由于顺序的错乱,对于查找失败的判断,还是要查找全部
- 还是要结合实际应用来决定哪一种查找优化
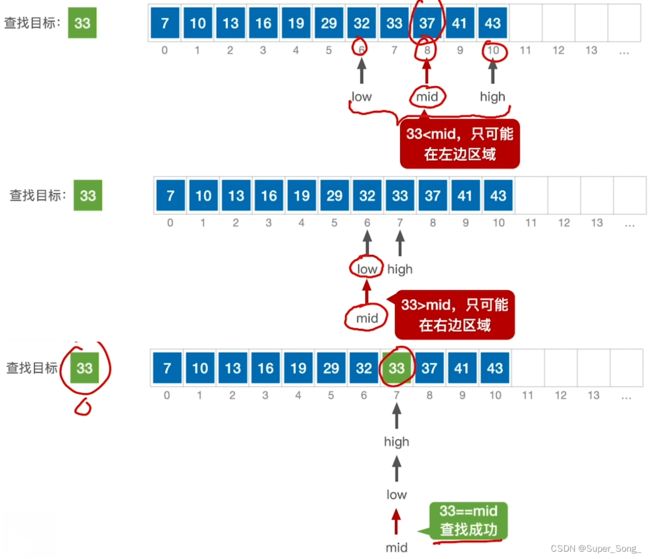
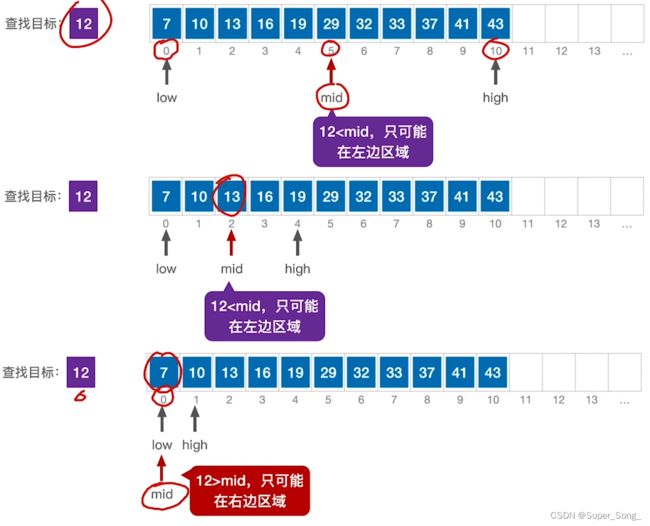
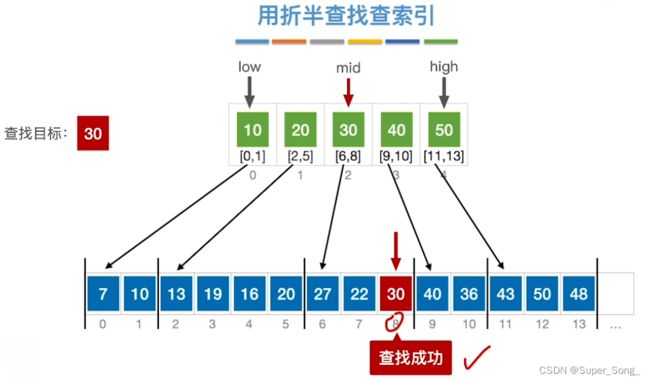
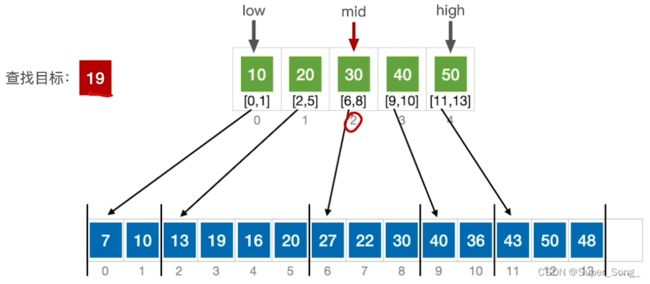
折半查找(二分法查找)–重要考点
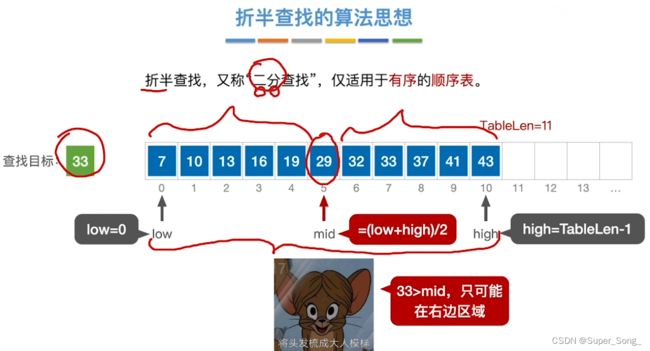
- 仅适用于有序的顺序表
- 查找成功过程
- 基于查找表是升序排列
- 仅适用于有序的顺序表,链表做不到,因为不能随机访问
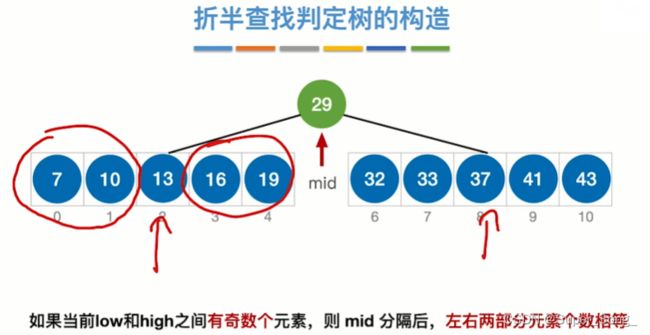
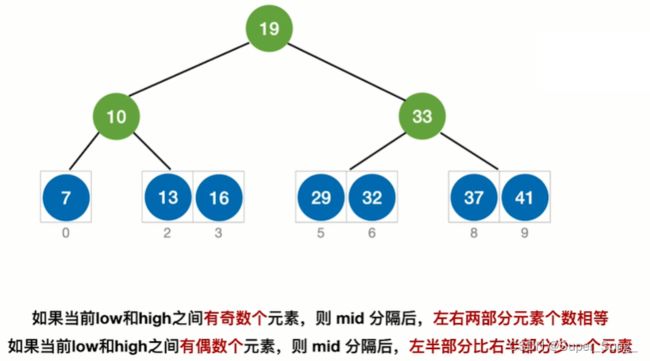
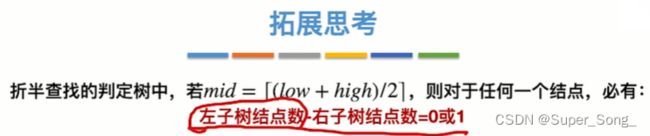
- 如果mid是向下取整得来的
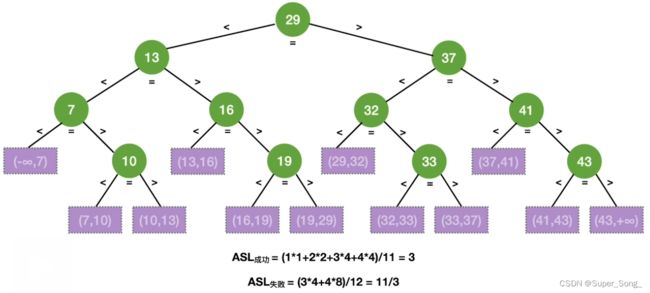
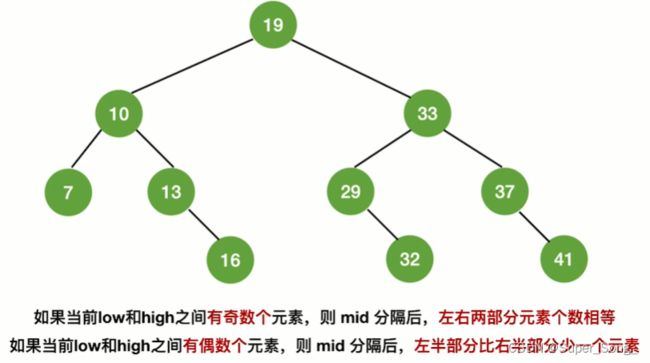
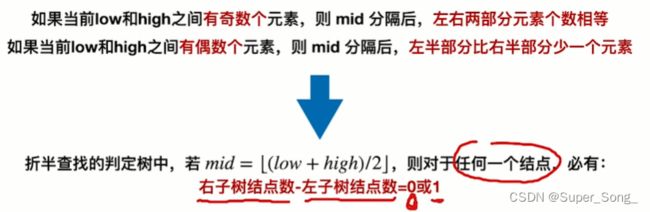
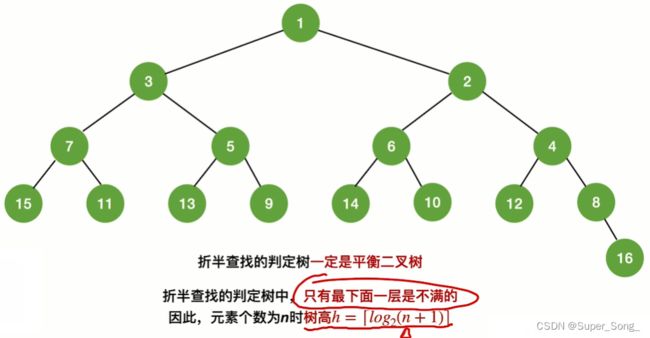
- 无论有多少元素,查找表所对应的折半查找判定树一定满足,右子树结点比左子树结点多一个,或者相等;否则就不对
- 所以已元素的个数,我们就可以推算出折半查找判定树长什么样
- 一定是个平衡二叉树
- 任意结点的左右子树的深度之差都不会超过1
- 只有最下面一层才可能是不满的
- 与完全二叉树的树高求法一样
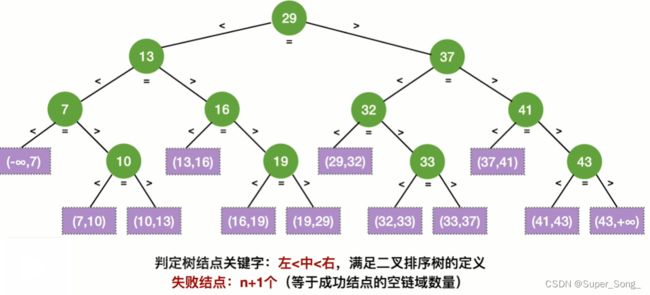
- 折半查找判定树的结构也符合二叉排序的特点
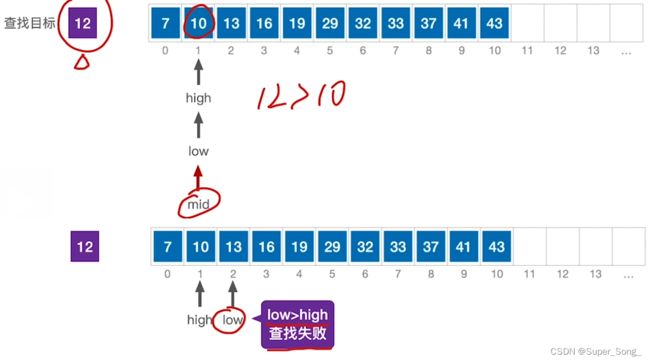
- n个结点的判定树,对应的失败结点判定是n+1个,
- 其实,这些失败结点正好连在了各个成功结点的空链域上
- 左子树的结点数就会比右子树多一个,或者相当
分块查找
选择题居多,重点介绍算法思想,能手算模拟即可
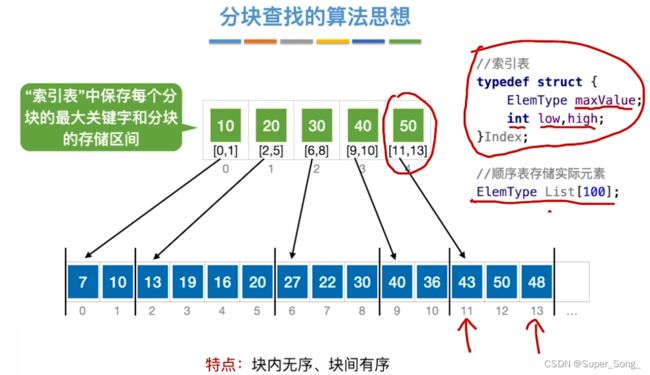
分块查找的算法思想
- 给定一组数据,看似无序,其实是,块内无序,块间有序
- 给查找表建立索引表,索引表保存每个分块的最大关键字和分块的存储区间
- 由于索引表本身也是有序且顺序存储,对索引表的查询可以采用折半查找
- 又称索引顺序表
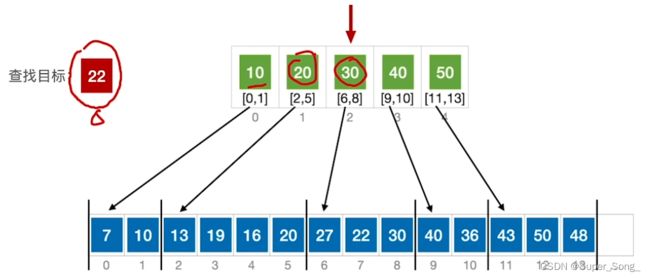
- 结合折半查找的代码来理解
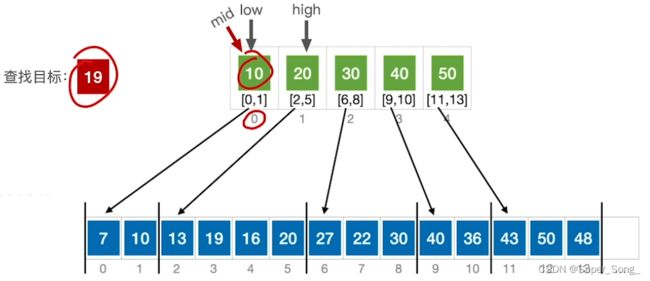
- 最终导致low>high,且low分块的最大值比high分块的最大值还要大,这个时候要进入到low的分块内查找
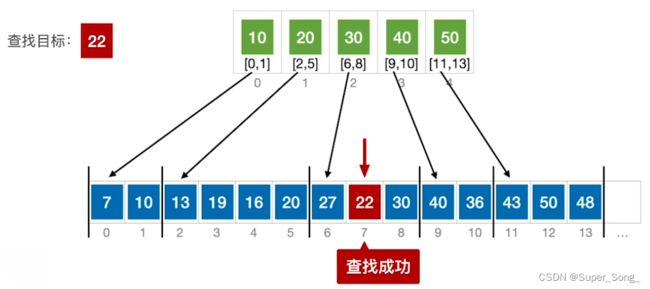
- 遍历块内元素,直到查找成功
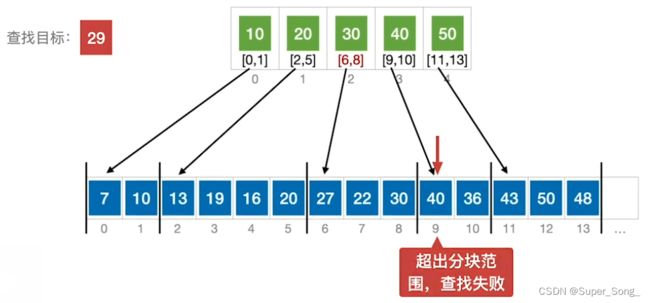
- 可能是目标关键直接超出了索引表范围
- 也可能是进入道分块内,遍历分块发现没有这个元素
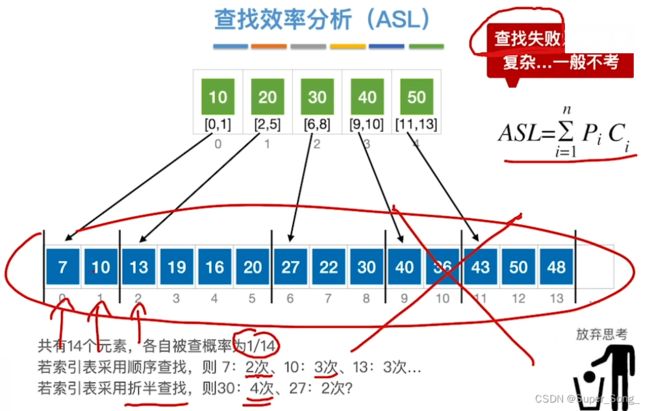
- n个元素,每个元素被查到的概率是n分之一
- 分别求出找到每个元素的所需的对比次数,求出数学期望
- 这样很麻烦,实际考试不会出这么复杂的情况
- 查找失败的效率分析情况更复杂,一般不考
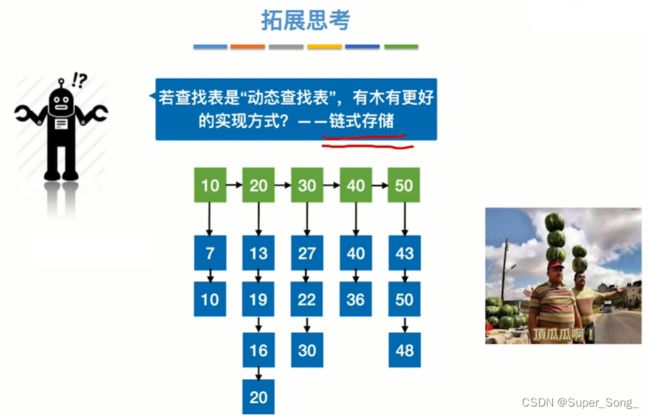
- 则索引表和块内元素都可以顺序查找,
- n个元素,分成b块,每块s个元素,n=sb
- 带入求出平均查找长度
- 给平均查找长度求导,得出最小查找长度
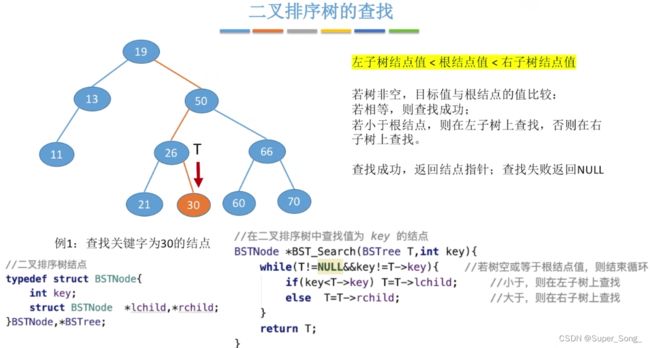
二叉排序树BST
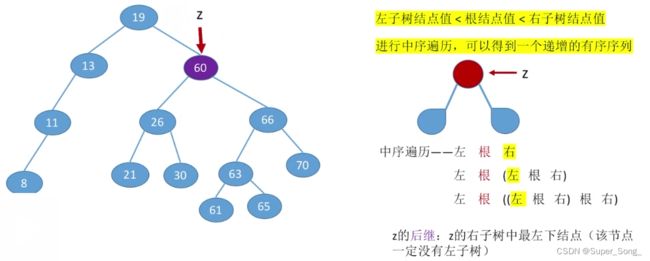
- 任意结点,左子树值<根结点值<右子树值
- 将二叉排序树中序遍历,得到的是递增的有序序列
- 适用于元素的有序组织,搜索
- 非递归实现效率更高,因为只调用一层函数栈,空间复杂度只有O(1)
- 注意不允许插入重复的结点
- 新插入的点一定是叶子结点
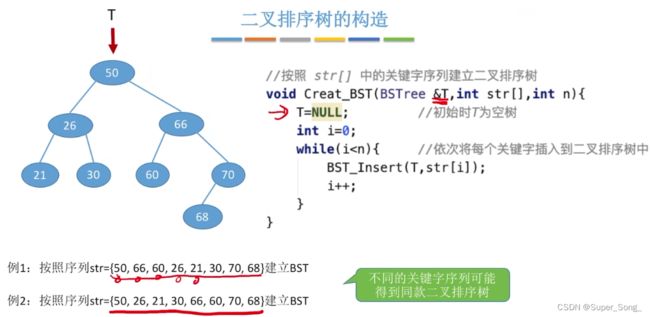
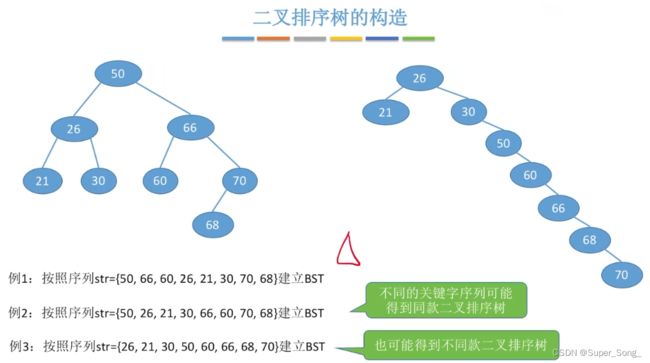
- 按照给定序列的默认顺序,构造二叉树
- 不同的默认顺序,可能会得到不同的二叉排序树
- 常考点,给定一组序列,构造二叉排序树
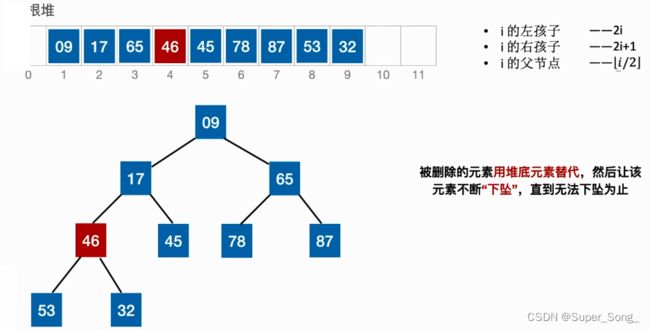
- 删除的叶子结点,直接删除,不会破坏二叉排序树
- 删除的是分支结点,分支结点只有一颗子树,删除后,让子树上来替代即可
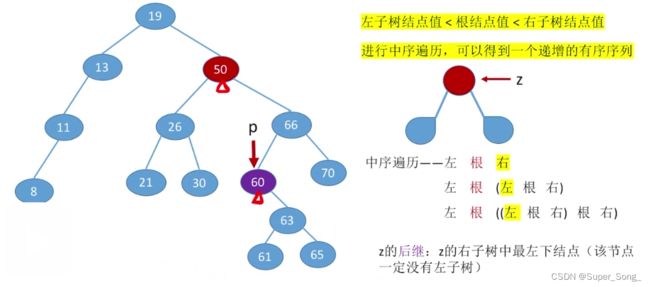
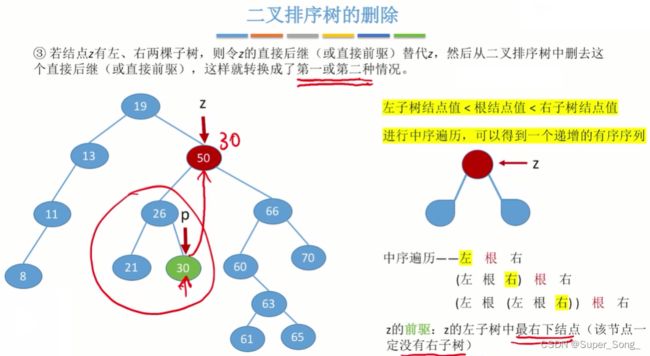
- 删除的是分支结点,在右子树找值最小的结点来替代,右子树中最左下的结点就是值最小的点;这个最左下的结点一定是没有左子树的,可能有右子树,再对这个结点执行删除操作
- 用左子树最大的值替代被删除的结点,也能实现功能
- 左子树最大的结点,就是左子树中最右下的结点
- 要重点关注,考试的重点
- 因为平均查找长度的数量级就是这棵二叉排序树的查找操作的时间复杂度
- 无论插入,删除操作,开始都需要查找操作
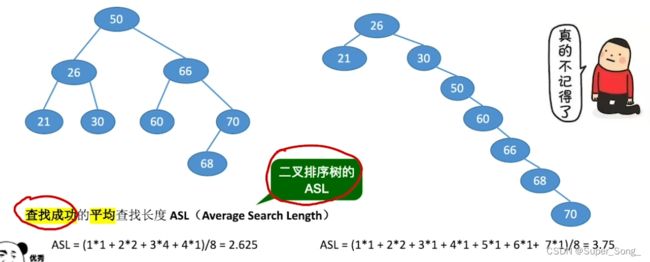
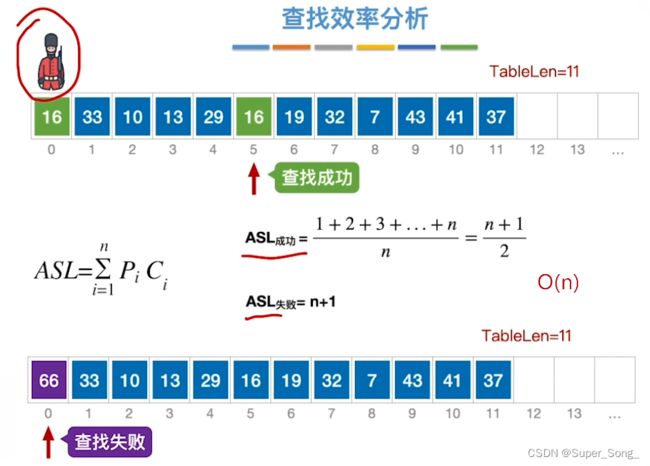
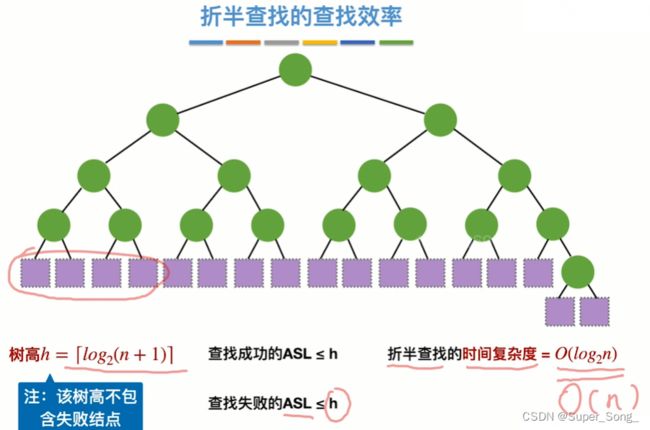
查找效率分析–查找成功
- 查找长度,就是需要对比关键字的次数,可以反应操作时间复杂度
- 计算平均查找长度
- 查找长度一定不会超过树高h
- 因此最好和最坏查找长度根据树高的最大和最小来确定
- 我们应该尽量降低树高,来降低查找长度
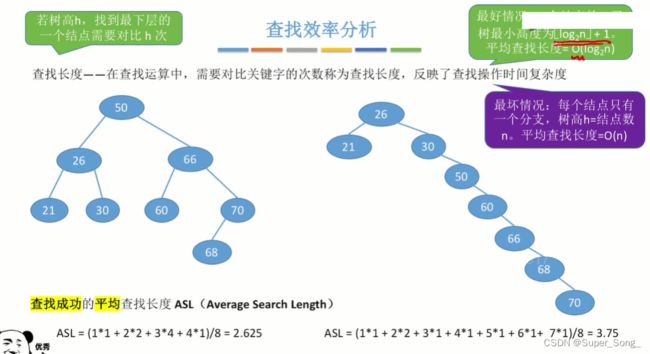
构建平衡二叉树可以尽可能减小树高
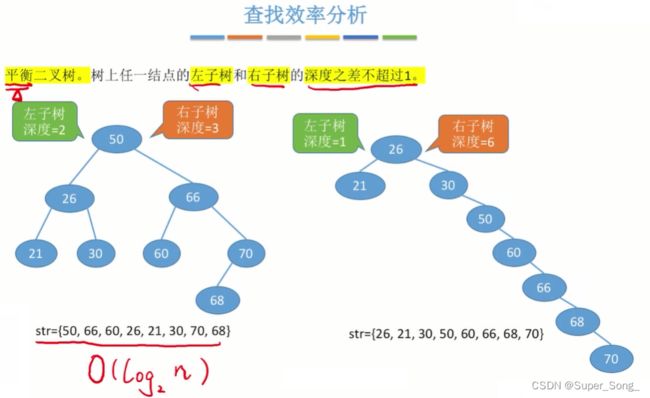
查找效率分析–查找失败

知识点小结
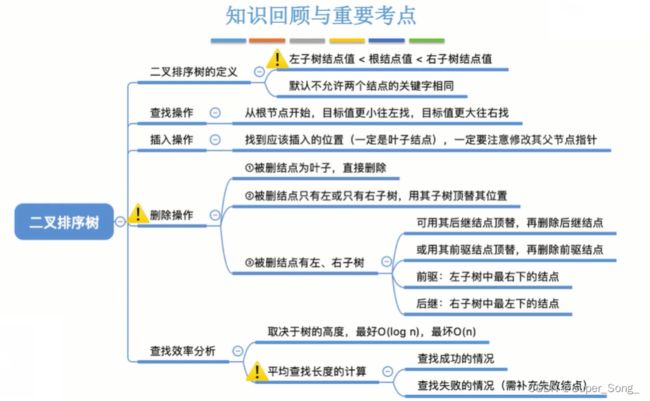
平衡二叉树–AVL–重要考点
- 考试可能出现缩写,注意和ASL平均查找长度区分
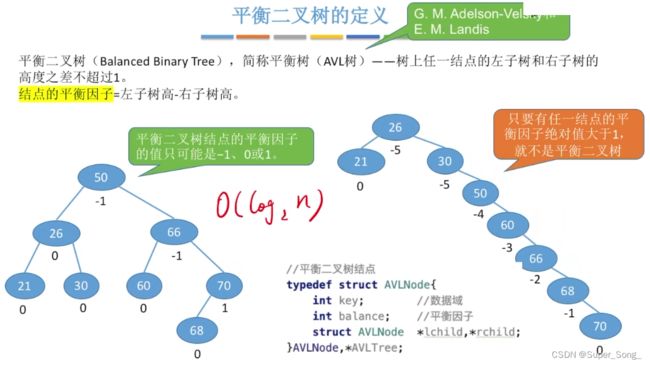
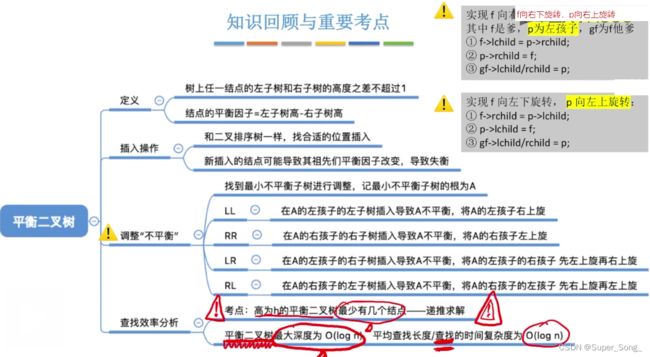
- 任意节点的左子树和右子树的高度之差不能超过1
- 结点的平衡因子 = 左子树高-右子树高
- 平衡二叉树的平衡因子的值只能是1 0 -1
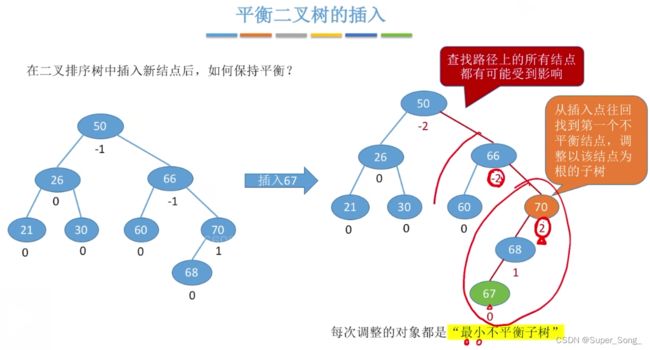
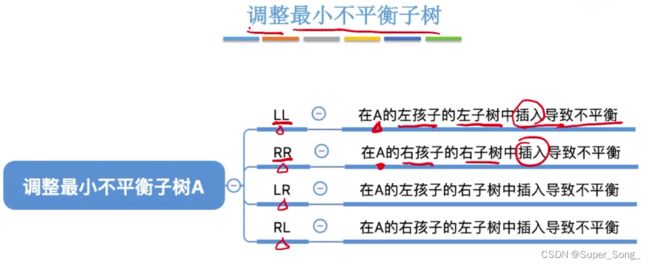
- 如何保持平衡
- 沿着新插入的结点往上游找祖先,直到出现第一个不平衡的结点
- 这个第一个出现的不平衡结点为根的子树,叫做最小不平衡子树
- 事实证明,只要把最小不平衡子树调整平衡,那么其他祖先结点都会恢复平衡
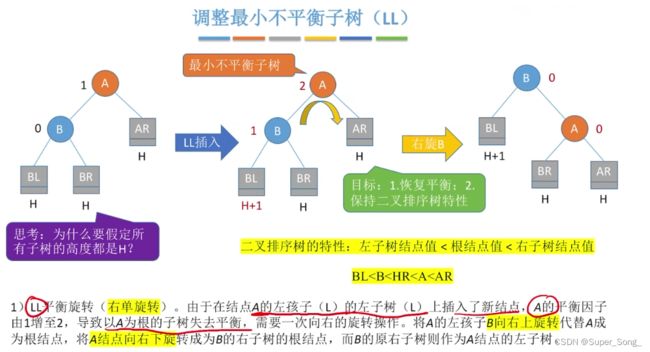
- 为什么要假定所有子树的高度都是H,因为只有这样,才会出现原来平衡,LL插入后不平衡
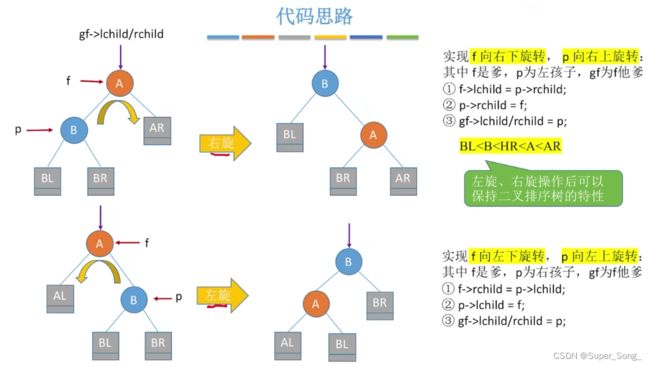
- 调整为平衡的目标:恢复平衡;保持二叉树的特性,即结点值的顺序
- 右旋B,再让B的右子树挂在A的左子树上
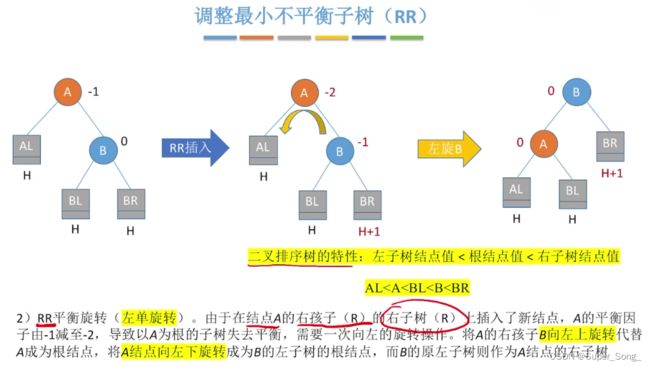
- 与LL的状态刚好左右对称
- 左旋B,再让B的左子树挂在A的右子树上
- 注意的指针替换的顺序,以免覆盖错了
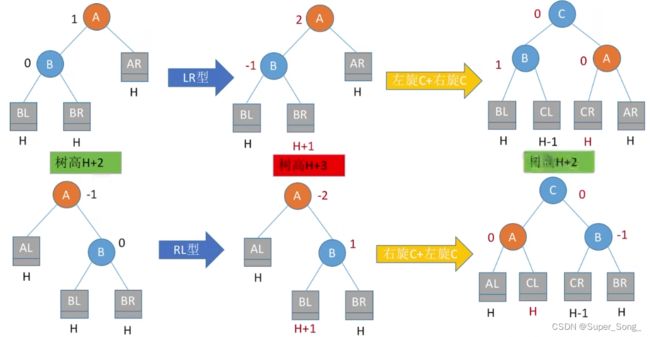
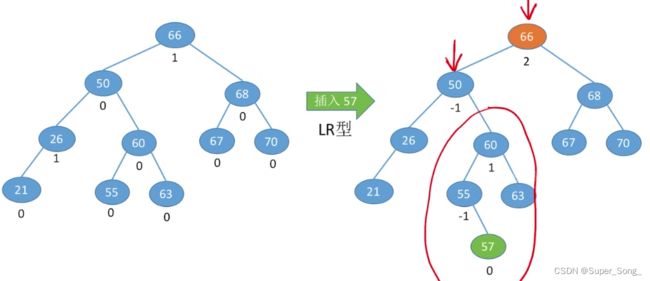
- 左孩子的右子树增加高度,导致出现了不平衡结点
- 还是假定所有的子树高度为H,原理同上
- BR的高度+1,导致了A成为不平衡结点
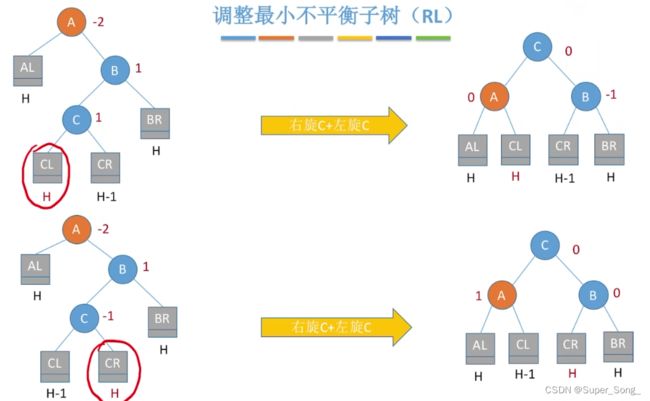
- 先把C结点进行左旋,再把C进行右旋;左旋和右旋的规则和前面基本一样
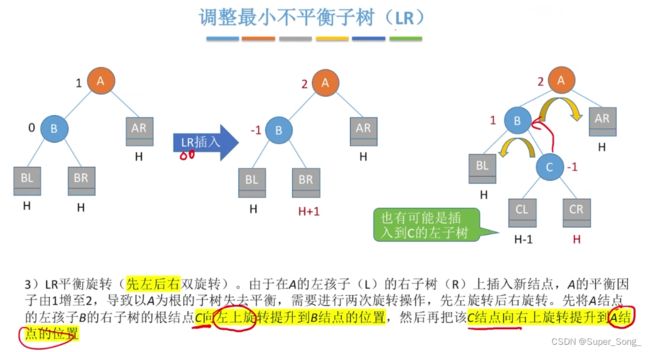

不论之前C是左孩子插入的,还是C是右孩子插入的,这样处理完都满足要求
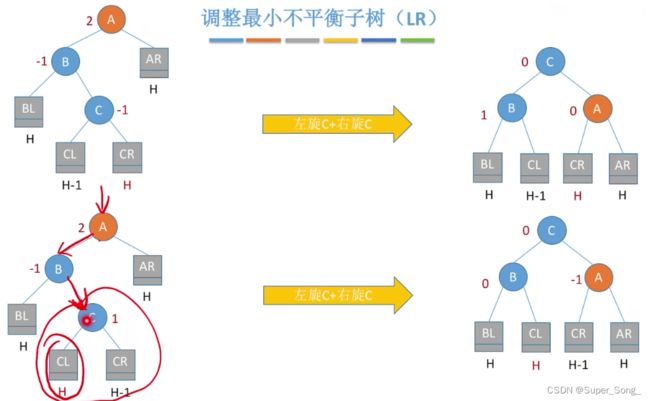
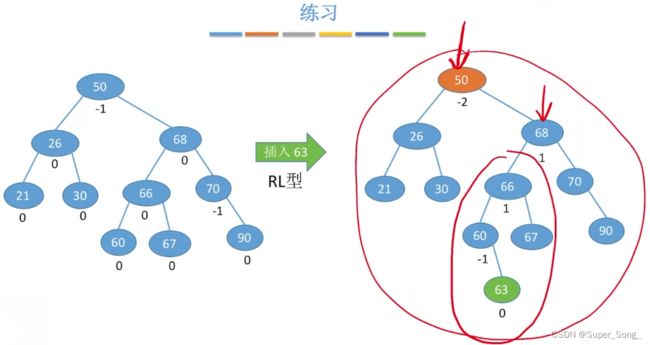
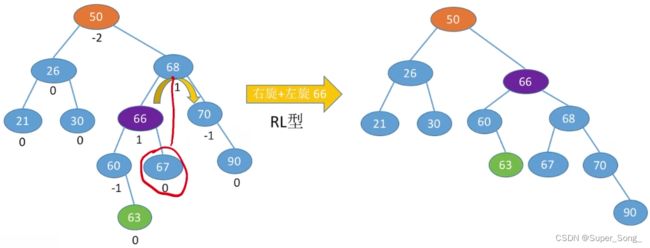
调整最小不平衡子树RL
- 处理方法刚好与LR的方法相对称
- 结合左右规律来记忆
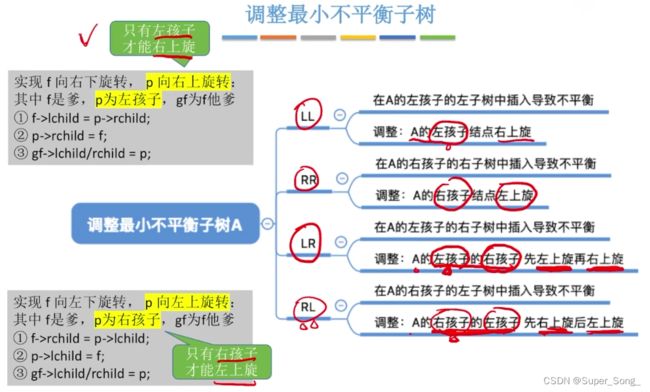
填坑-开头的问题如何解决
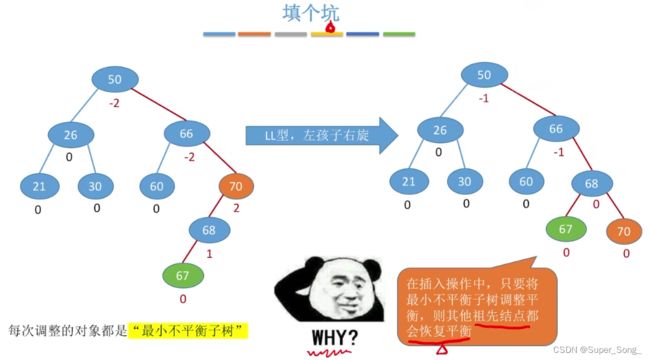
为什么只要将最小不平衡子树调整平衡,其他祖先结点就会恢复平衡
- 正是因为插入操作,导致了这个结点的高度+1,成为了最小不平衡结点
- 调整过后,这个结点的高度恢复为H,对于上面的父结点,高度也都不会变化
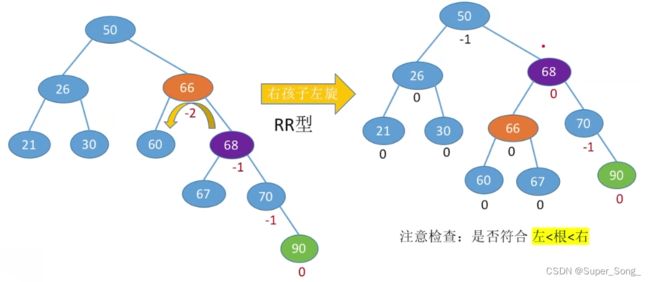
![]()
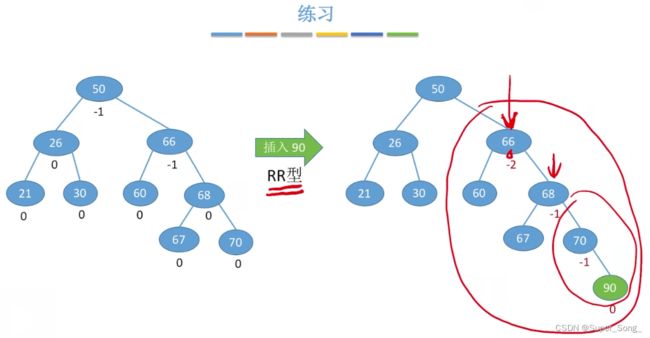
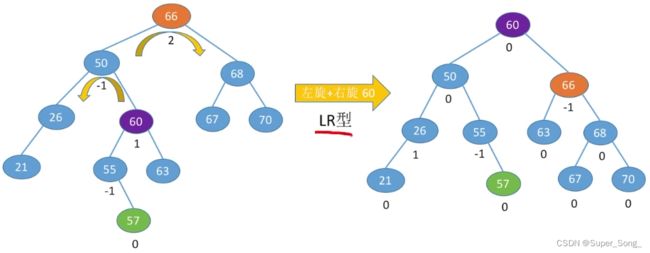
- 其实熟练以后可以一步到位的移动
- 本例中,60的左子树作为50的右子树,60的右子树作为66的左子树;
- 最后,60成为根结点,左右分别是50的子树,68的子树
- 看树高,时间复杂度不会超过O(h)
- 理解递推公式的含义,结点总数=左子树结点数+右子树结点数+根结点
- 有了递推公式,给定一个平衡二叉树的结点数,可以得出最大树高h
- h就是最坏情况,最大的查找长度
- 即平衡二叉树的最大深度为O(log2n),如何由递推公式得到这个,不好证明,记住就好
平衡二叉树的删除操作
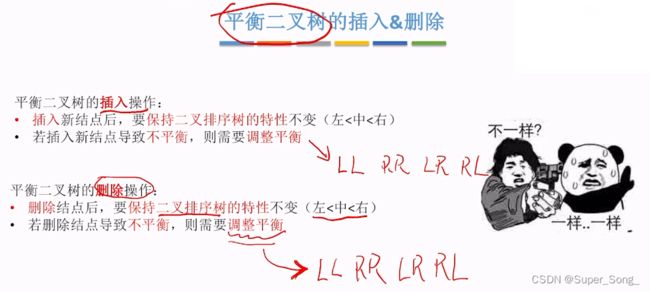
- 首先保证删除结点后,二叉排序树的特性不变
- 若删除结点导致不平衡,再调整平衡
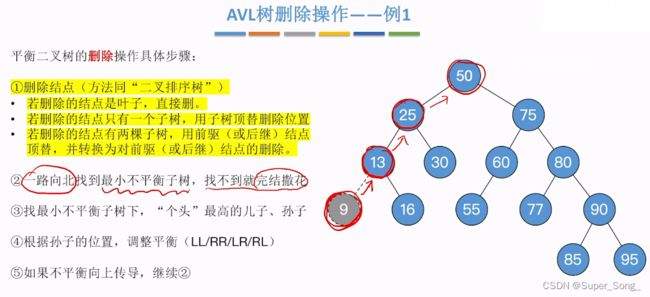
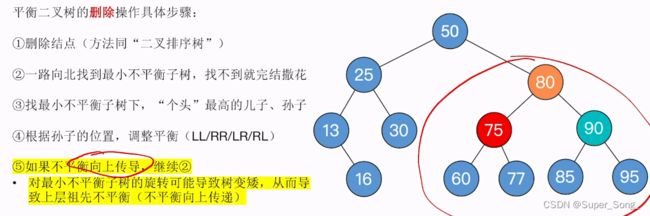
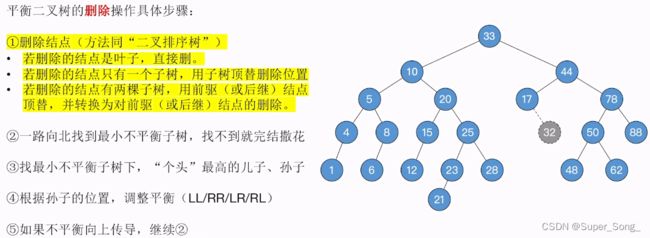
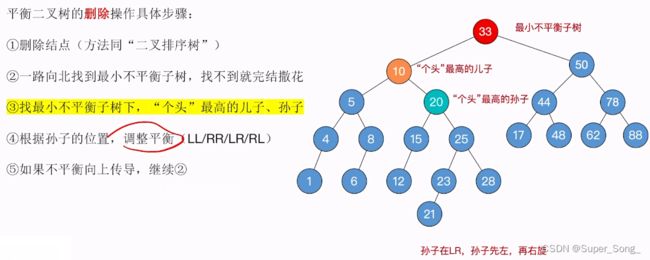
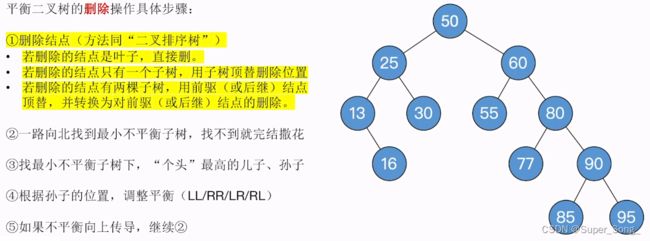
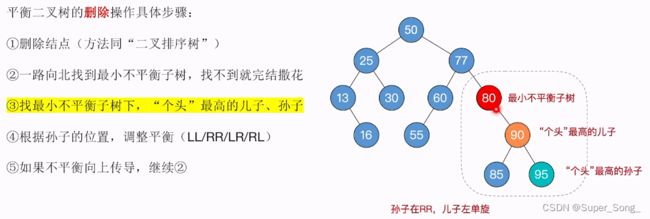
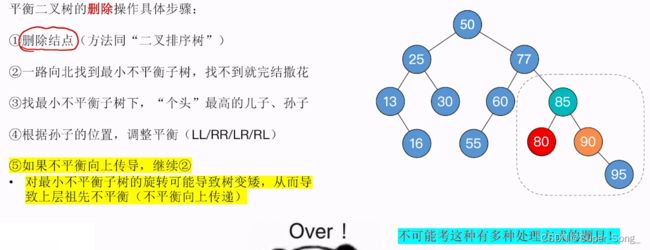
- 平衡二叉树的删除步骤:
- 1.正常执行二叉树排序树删除结点的操作,(前面的小结有具体步骤)
- 2.从被删除的结点开始,向上找,找到最小不平衡子树,早不到就拉倒
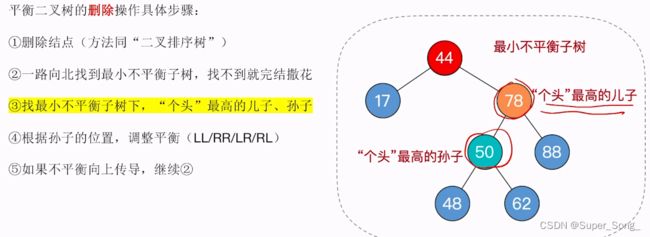
- 3.找到最小不平衡子树,下面,个头最高的儿子,孙子
- 4.根据孙子的位置,调整平衡(LL RR LR RL),调整方法与前面的插入一模一样
- 5.如果调整导致了不平衡向上传导,则继续2步骤的操纵
- 删除9号,没有造成任何不平衡结点,删完不做任何调整
- 删除55,基于上一个树继续
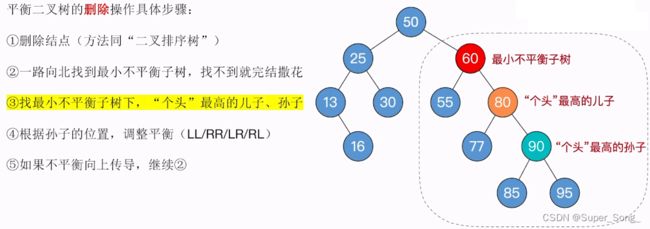
- 发现75结点出现最小不平衡子树
- 找到75下边个头最高的儿子,也就是80右子树;在从这个个头高的儿子下边,找个头最高的孙子,即90右子树
- 根据这个孙子结点的位置,决定选择哪一种类型调整,调整方法遵循前面的LL RR LR RL
- 不难发现,这个RR型,需要对80结点进行左旋操作
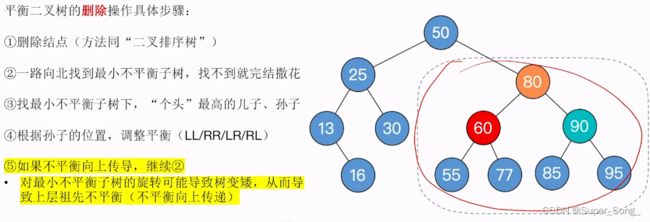
- 调整后,红框内已经恢复平衡,且高度-1,但是有可能导致上级祖先结点不平衡,还要向上检查
- 不难发现,这里没有出现问题,调整结束
- 删除32结点
- 找到最小不平衡子树结点32,找到下面个头最高的儿子,孙子
- 根据孙子的位置发现,这个RL型,需要对孙子先右旋,再左旋
- 调整过后,二叉树恢复了平衡,调整完毕
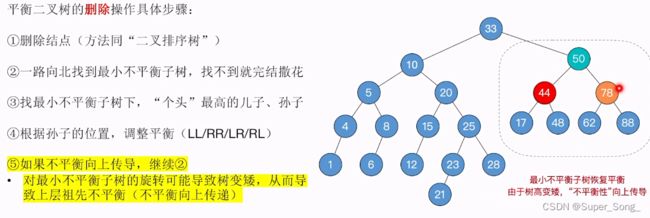
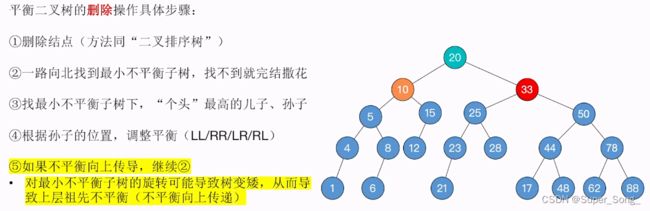
- 本例中的右子树与例3一样,
- 还是删除32结点,先出现然44子树不平衡,后按照例3进行调整,得到新的50子树平衡
- 但是,不平衡向上传导,导致整个33子树不平衡
- 继续重复第二步操作,从50结点向上找到最小不平衡子树33
- 找到33下面个头最高的儿子,孙子,然后开始调整平衡,显然这是LR型
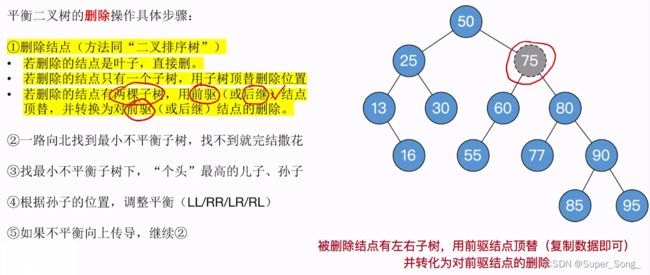
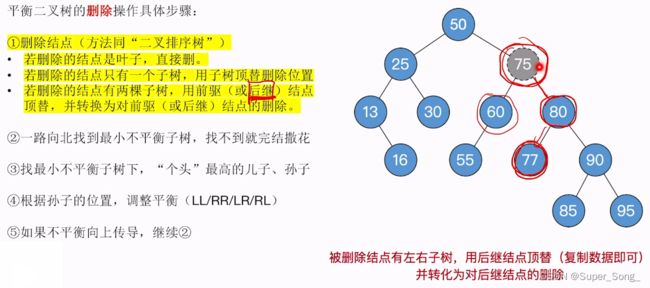
- 删除75结点,删除规则要按照二叉排序树的规则来删除
- 可以用75的前驱或者后继来顶替75结点的位置
- 1.如果采用75的前驱,就是找75左孩子的最右下
- 75左孩子的最右下是60,把60的数据覆盖在75上
- 对75的删除转为对前驱结点60的删除,
- 此时60只有一个子树,删除旧的60以后,子树顶上即可;这里的顶替不是数据的复制,而是让55实体挂到新的60上面;释放旧的60结点
- 由于刚才删除的其实是就得60点,也就是新的55结点位置,所以从55结点向上找最小不平衡子树
- 找到60,对60子树进行调整,执行RR型操作
- 调整完毕,检查不平衡性是否向上传导
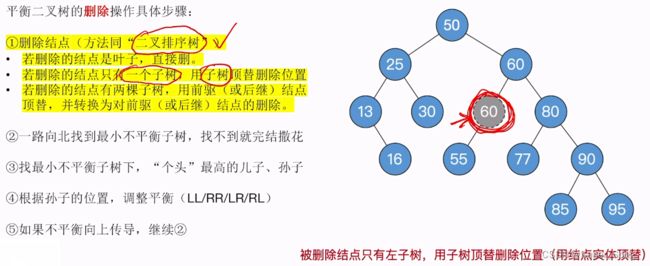
- 删除75结点,删除规则要按照二叉排序树的规则来删除
- 可以用75结点的前驱或者后继来顶替75结点的位置
- 2.如果采用75结点的后继,就是找75右孩子的最左下
- 找到75的后继是77,将77的数据覆盖到75上,转化为对旧的77的删除操作
- 77是叶子节点,直接删
- 77的删除导致80结点成为最小不平衡子树,因此对80子树进行调整
- 80的孙子有两个,选谁都一样
- 考试基本不会出现这种有争议的结果
- 这里删除之后,检查发现并没有出现不平衡,删除完毕
- 咸鱼认为,考试应该不至于出到删除并调整之后,还要向上传导的情况;能掌握最好
- 重点掌握1.2.3,理解4,了解5.6
- 2022年之前没有考过,以后考的概率也比较低
红黑树–RBT
为什么要发明红黑树
- 二叉排序树,平衡二叉树,红黑树都是用于查找
- 如果对平衡二叉树插入或删除,很容易导致不平衡,需要频繁调整数的形态,时间开销较大
- 而对红黑树的插入和删除,不会破坏红黑特性,无需频繁调整树的形态,调整的时间开销也较小
- 平衡二叉树适合:查找多,增删少的场景
- 红黑树适合:增删多的场景,实用性更强,2022年新增考点
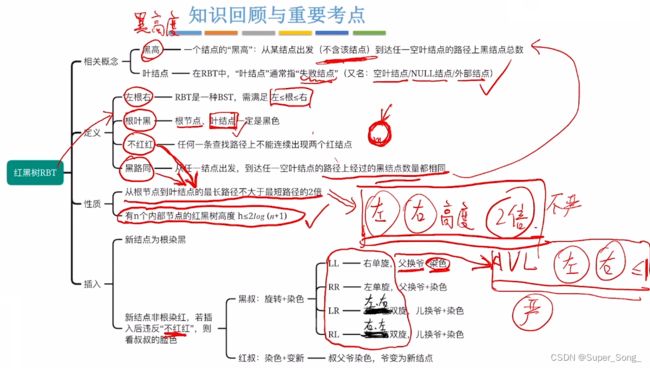
- 红黑树是二叉排序树的优化,首先它是二叉排序树
- 红黑树比普通二叉排序树多了一些要求
- 每个结点是红色或黑色
- 对比平衡二叉树,AVL存的是平衡因子,RBT存的是颜色
- 根结点固定为黑色
- 叶结点为黑色,这里的叶结点,不是我们说的叶子结点,而是查找失败结点,外部结点,null结点
- 不存在两个相邻的红结点,相邻指的是指针的直接指向,兄弟结点不算
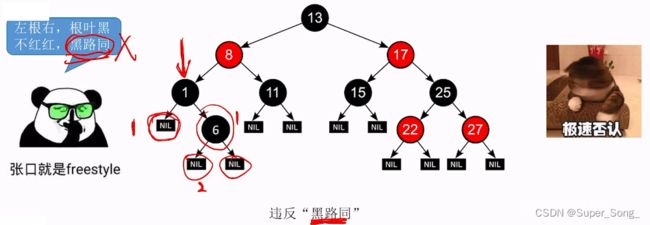
- 对于每个结点,从该结点出发,到任意叶结点的简单路径上,所含黑结点数目相同
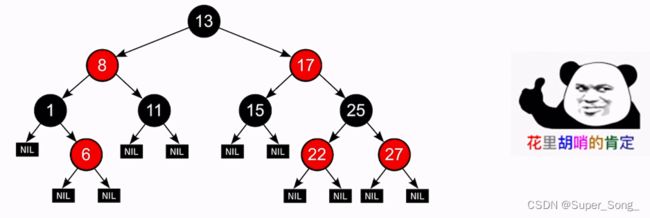
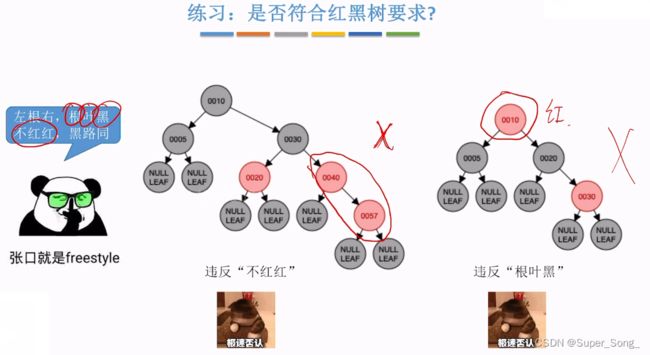
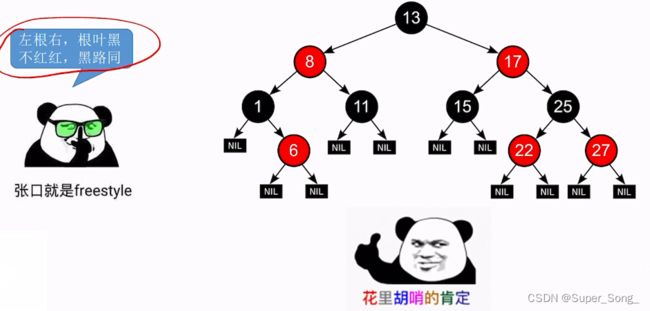
- 口诀:左根右,根叶黑,不红红,黑路同
- 1.根结点到叶结点的最长路径不大于最短路径的2倍
- 首先根结点到叶结点的各个路径,包含的黑结点数相同
- 路径最长的情况就是红黑穿插,路径最短的情况,就是没有红色
- 2.有n个内部结点的红黑树的高度h<=2log2(n+1),证明过程暂时不管
- 得到了树高,就能得出查找操作时间复杂度为O(log2n)
- 与BS和AVL相同,从根出发,左小右大,若查找到一个空叶子节点,则查找失败
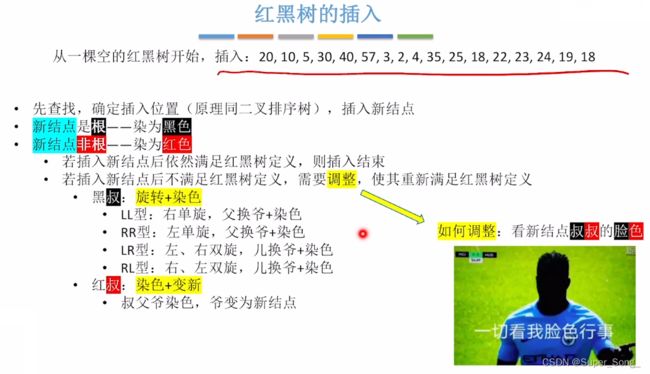
红黑树的插入
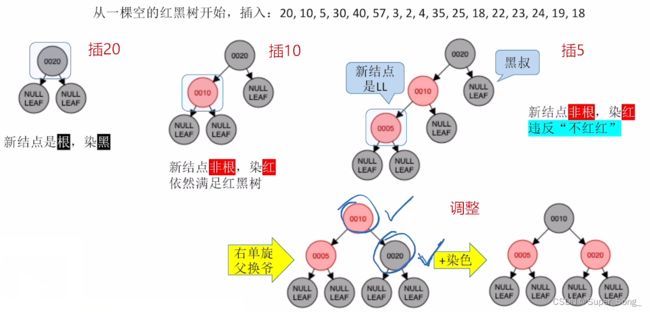
- 思考:为什么插入新结点,除了根结点,要染红色?
- 因为如果插黑色,一定会导致本路径黑结点总数增加,破坏黑路同的规矩;插红色不影响
- 黑叔:旋转+染色
- LL型:右单旋,相当于父10上位,爷20下去;父爷再分别染色,即取反,红变黑,黑变红
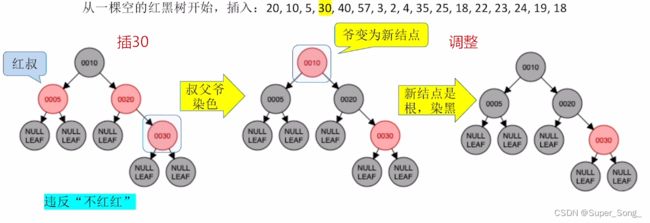
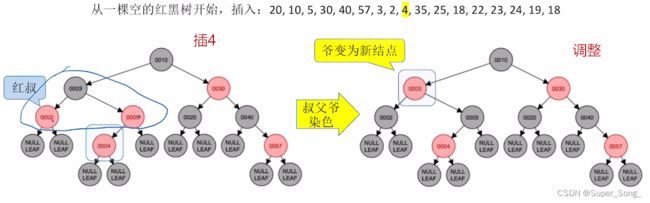
- 红叔:染色+变新
- 叔父爷染色,即都取反,黑变红,红变黑
- 爷结点此时视为新增加的结点,如果为根,就染黑,如果不为根,就染红;
- 再检查这个“新增”的爷结点,是否满足红黑树定义;满足则拉倒,不满足,则基于这个“新增”结点,继续调整
- 插入结点,如果违反红黑树定义,一定是违反了“不红红”
- 左根右,不可能,本来就是按位置插的;
- 根叶黑,不可能,如果插的是根,本来就给黑色,叶结点本来也一直都是黑色
- 黑路同,不可能,因为插入的不是根,则给红色,不会增加路径上的黑结点
- 所以插入非根结点,重点关注是不是违反了不红红
- 出现违反,且黑叔:旋转+染色
- RR型:左单旋,相当于父30上位,爷20下去;父爷再分别染色,即取反,红变黑,黑变红
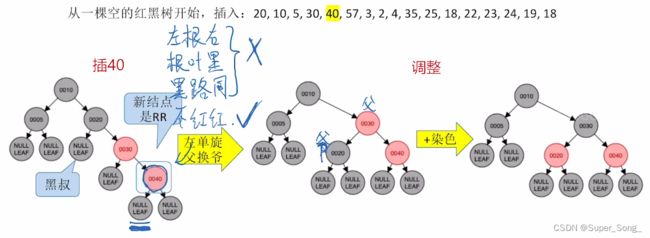
继续插入,重复的情况直接跳过
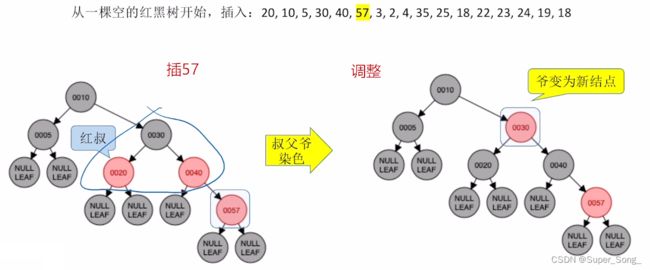
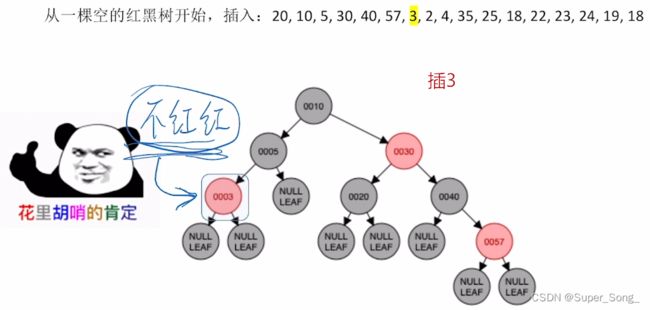
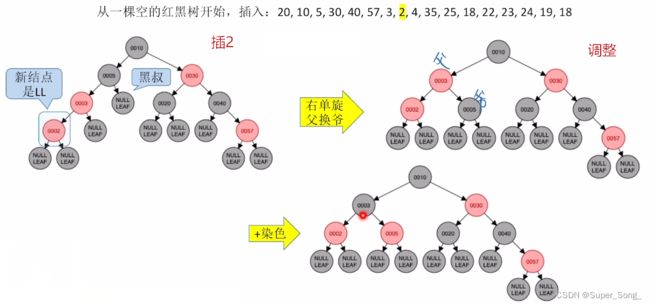
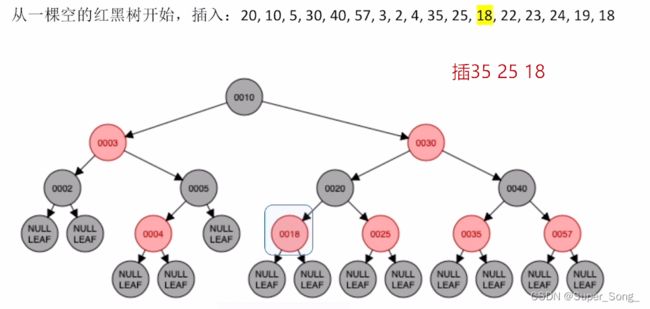
当发现根结点是红色时,直接染黑

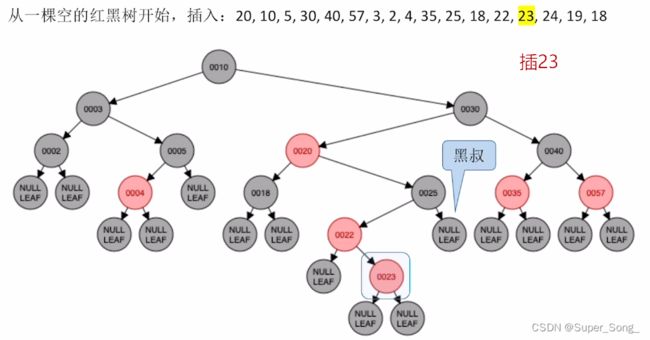
- 黑叔:旋转+染色
- LR型,左,右双旋,再对原来的儿和爷染色,即取反
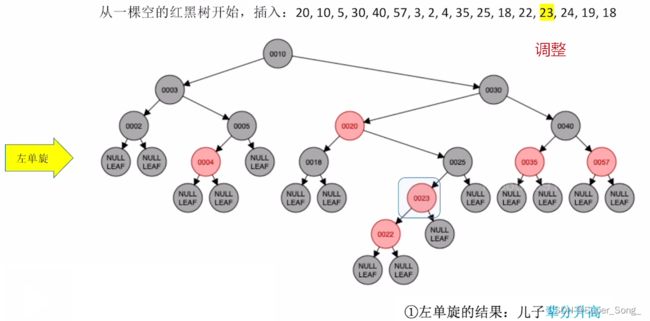
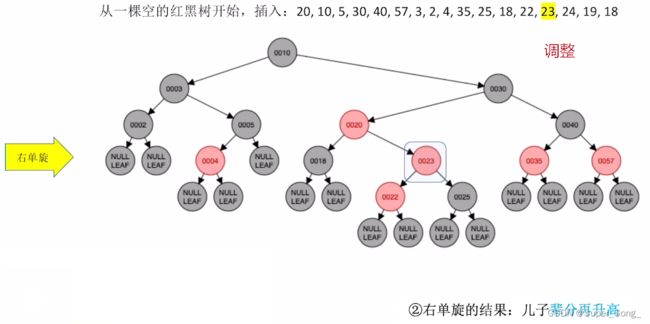


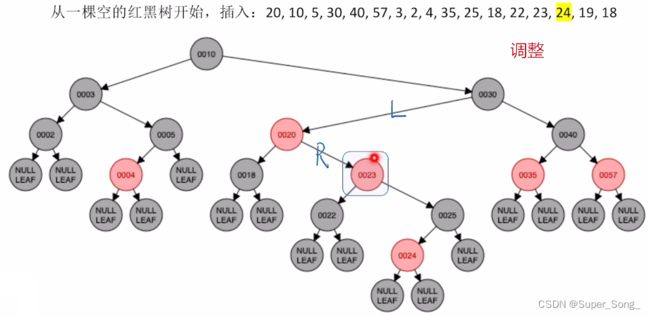
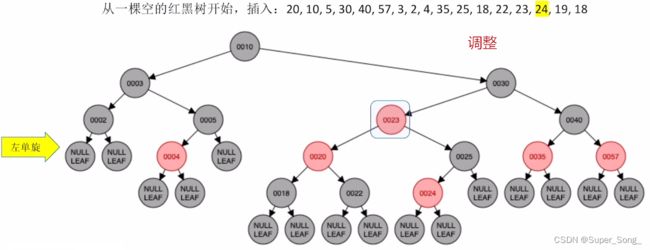

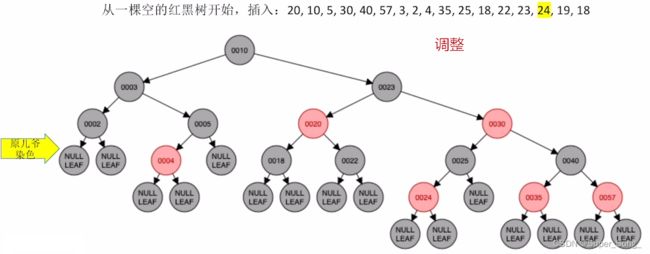
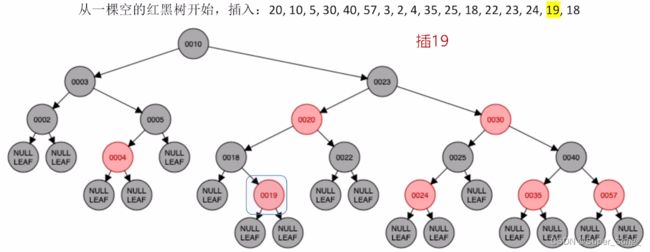
遇到插入重复的元素,根据自己情况决定;比如这里放在了19的左下

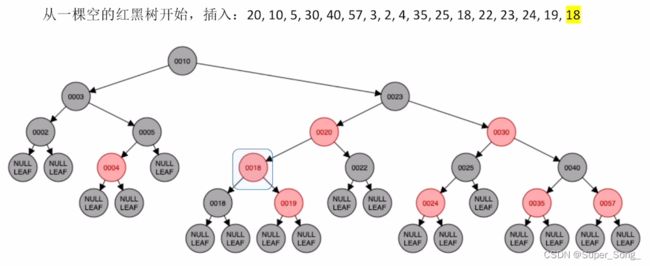
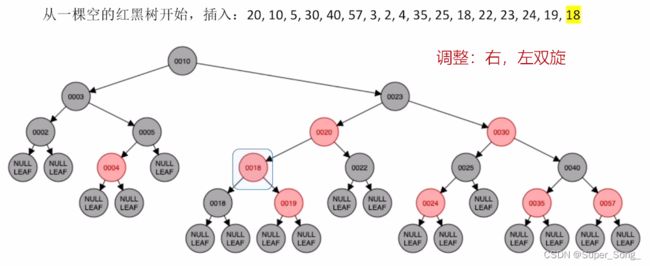
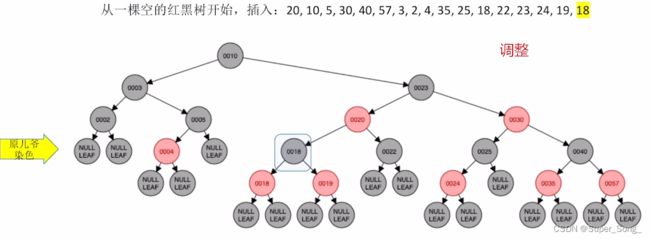
知识点小结
- 本例覆盖了所有红黑树插入的调整情况,考试不可能考这么复杂的树
- 所谓的叶结点就是个空指针,视为黑色结点,有利于我们分析红黑树
- 从根结点到叶结点的最长路径不大于最短路径
- 由此延伸,一个结点左右子树高度差,不会超过两倍,相对来说条件不算苛刻
- 平衡二叉树则要求不能超过1,相对而言比较严格,所以调整起来就会很频繁
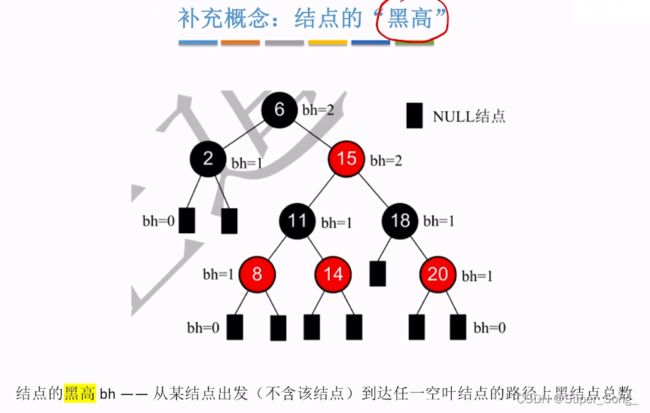
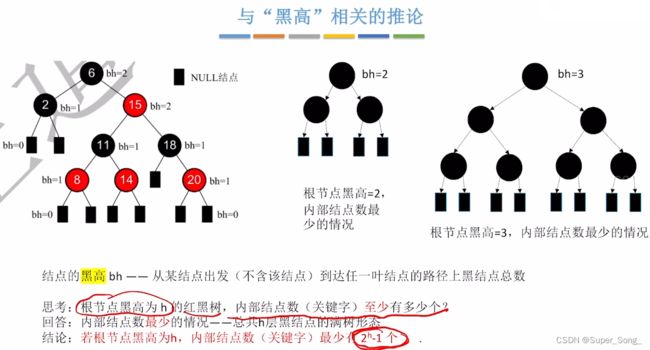
- 黑高:从某结点出发,到达任意叶结点的路径上黑结点的个数
- 思考:根结点黑高为h的红黑树,内部节点至少有多少个;内部节点指有实体的结点,排除掉null结点
- 答案:内部结点最少的情况,总共h层黑节点的满树形态
- 全为黑节点可以理解
- 为什么是满树,因为如果不为满树,某些地方为空,就会导致黑路同不符合要求
- 若根结点黑高为h,内部结点数最少有2的h幂-1
红黑树–删除操作
红黑树的删除操作比插入操作还要难很多
- 22年刚上考纲,23 24年不可能考红黑树的删除,不建议深入学习
- 最多考红黑树的定义,性质,选择题型
B树
考点
- 咸鱼认为是数据结构排名前三的难点
- 侧重考查B树的性质,插入,删除,查找的手算操作,代码一般不要求掌握
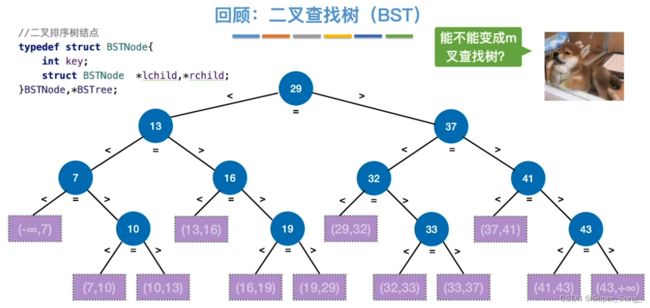
回顾二叉查找树BST
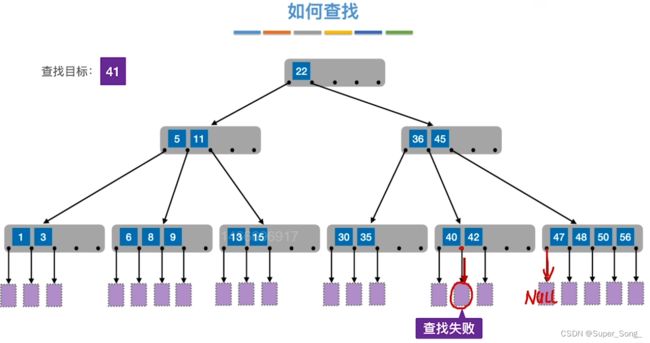
- 二叉查找树其实就是,不断的将查找范围分成两部分
- 思考:能否由二叉查找树扩展为5叉查找树
- 原理和二叉查找树都是类似的
- 如果结点有一个关键字,就把当前所在区间分成两个区间;如果结点有两个关键字,就把当前所在的区间分为三个区间;以此类推
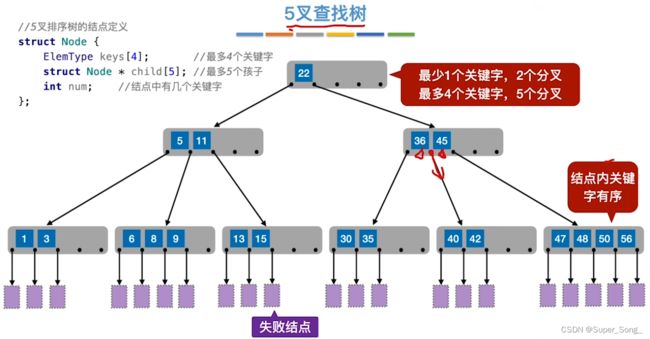
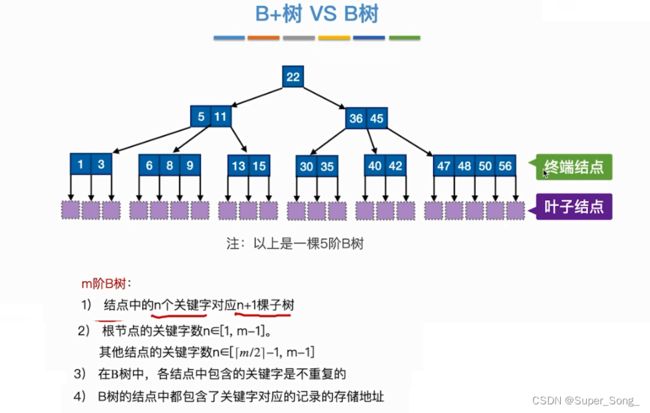
- 结点的定义:最少1个关键字,2个分叉;最多4个关键字,5个分叉;结点内的关键字是有序的
- 如果查找落在失败结点的范围,即查找失败
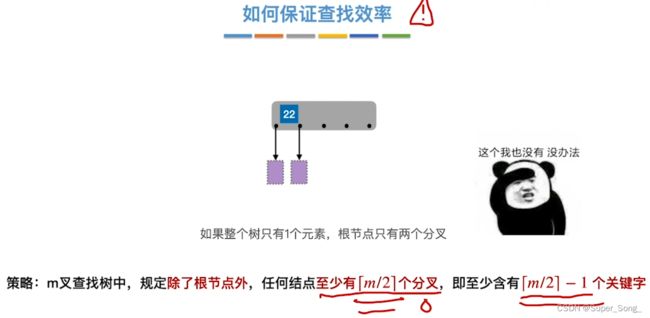
- 每个结点内关键字越少,树就越高,查找的层数越多;
- 所以可以指定策略,尽量增加结点内关键字个数,降低树高
- 根结点除外,因为如果整个树只有一个元素,就保证不了分叉个数
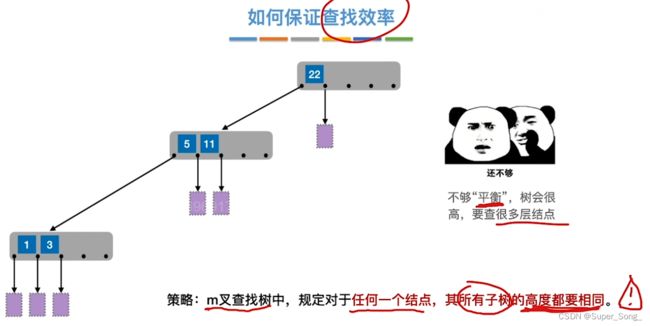
- 如果查找树不够平衡,也会导致树高过大,查找效率低
- 可以借鉴平衡二叉树的思想,限制子树的树高之差
- 由于多叉查找树限制子树的树高之差不超过1会很麻烦,所以直接简单粗暴规定,子树树高必须相同
- 规定任何结点至少有一定的分叉数量
- 绝对平衡,子树树高必须相同
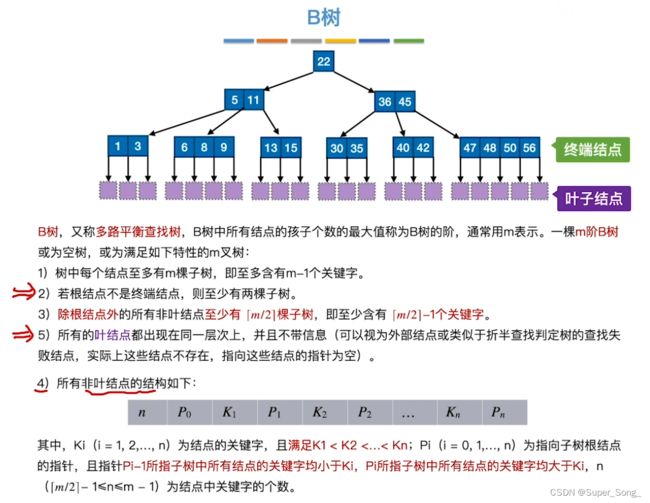
- 我们习惯将最下面的含有实际数据的结点成为终端结点,最下面的失败结点称为叶子结点
- 注意理解每一条的含义,这些含义,在前面的举例中,已经都包含在内了
- 第一次学习B树就直接看定义,会很懵,因为要求太多
- 课本方法
![]()
B树的插入和删除
插入举例–5阶B树
- 明确一点,5阶B树,每个节点最多4个关键字,5叉
- 在一个节点中,关键字与分叉指针是交替相间的
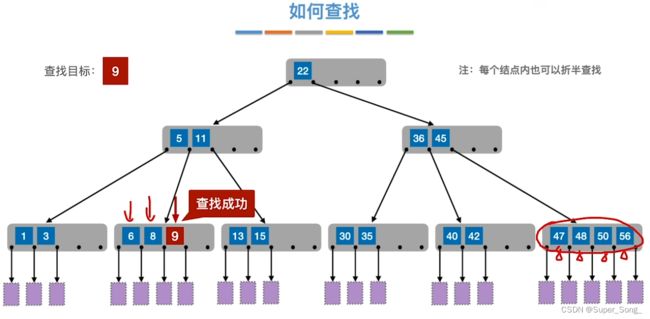
- 查找时,遍历当前节点,找到关键字就是找到了;没找到关键字,就进入到,对应区间的分叉上去,进入到下层继续查找

插入25,38,49,60,正常存入结点,插80,结点满了,开始分裂结点

从中间开始分裂,中间节点49提上去,作为父结点;注意,新插入的元素一定是先插到最底层,有调整那是后话
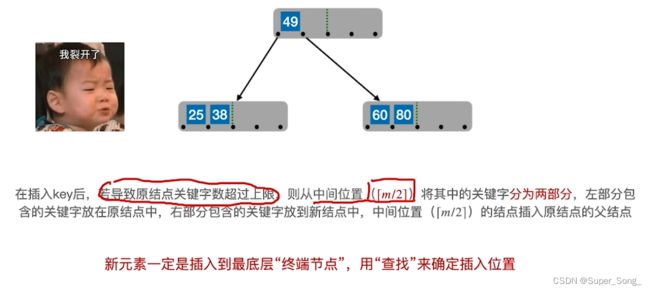
要确保错误节点只能在最底层;如果90插到错误位置,会导致错误结点出现在上面
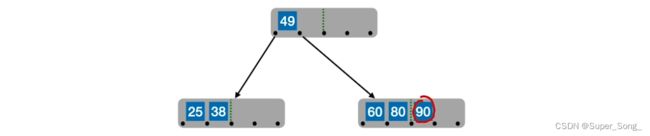
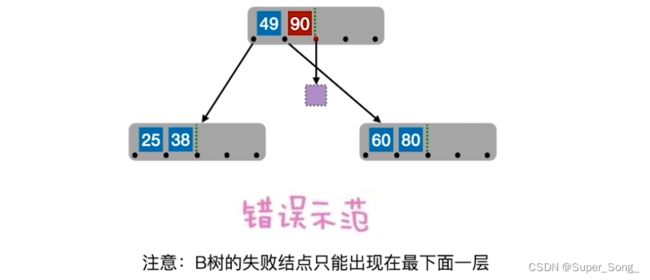
插99,正常;插88,节点满了
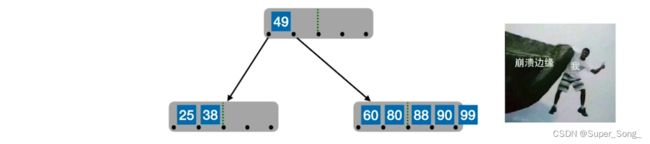
从中间结点88开始分裂,提升为父节点;父节点里还有坑位,正常存入88
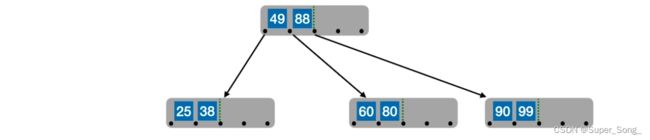
插入83,87,正常进入结点,插入70,结点已满,开始分裂
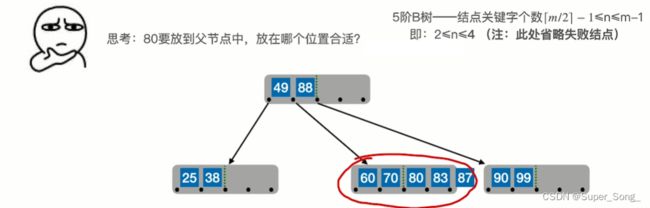
80提升到父节点,也要满足父节点关键字有序排列;即,80应该放到原本这个指针的右侧位置上
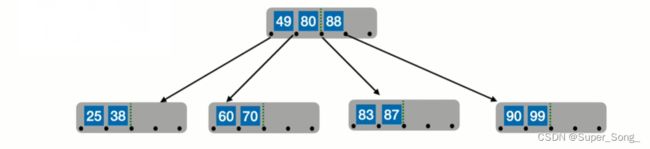
插入92,93,94,结点已满,需要分裂
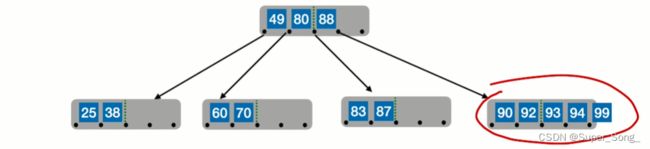
把93提升到原本这个结点所对应的指针的右边,也就是88右侧的指针的右边
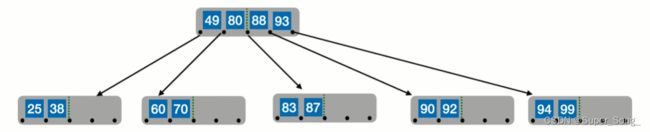
插入73,74,75,结点已满,需要分裂
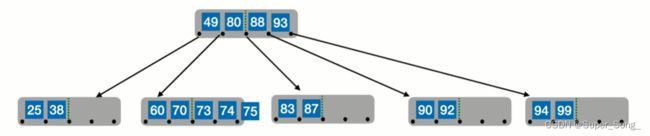
分裂之后,73提升至父节点,父节点已满,需要分裂

与之前的分裂一样,提升父节点,如果没有上一级结点,就新建结点;根结点可以只有一个关键字
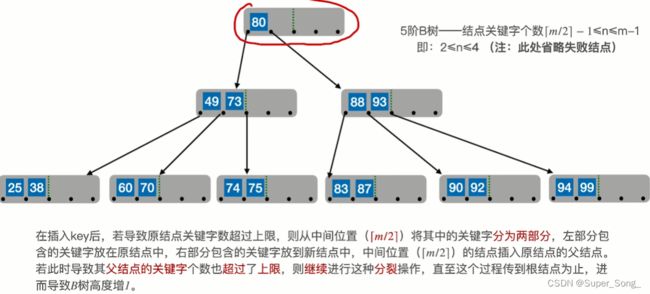
B树插入小结
- 除了根结点之外,其他结点应满足关键字个数
- 子树中的关键字与结点上的关键字应满足数值的顺序
- 新元素插入,一定是先插到终端结点,用查找来确定位置;后续再根据需要提升结点
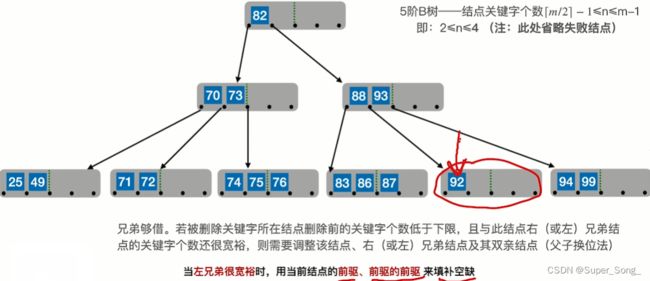
删除60,60在终端,正常删;删除后,结点总数符合要求
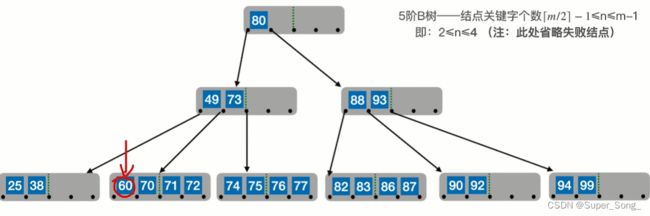
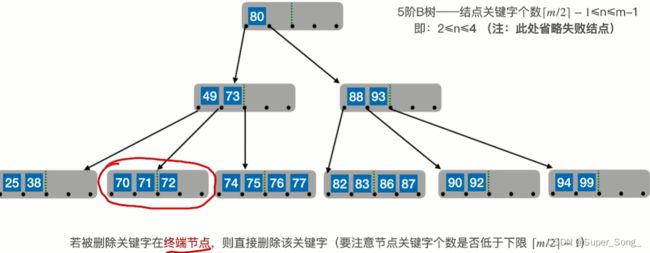
删除80,80不是终端结点;需要使用80的直接前驱或直接后继来顶替
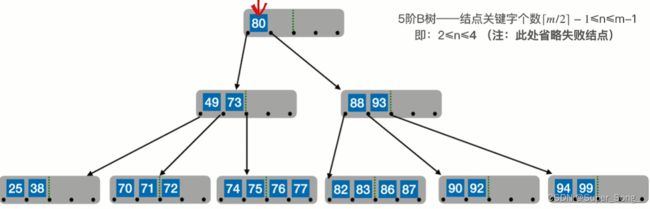
如果使用80的直接前驱77来顶替,即80的左侧的指针所对应的子树,的最右下
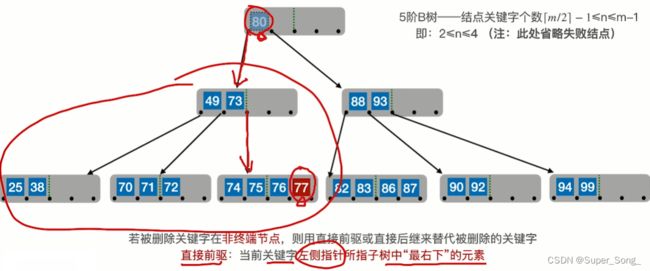
这种操作,相当于对非终端的操作转换成了,对终端节点的操作
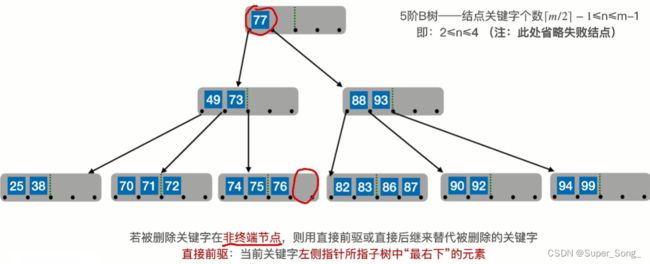
继续删除非终端结点77,这次使用77的直接后继82来顶替
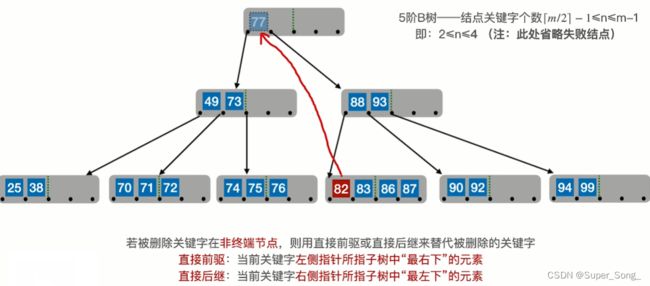
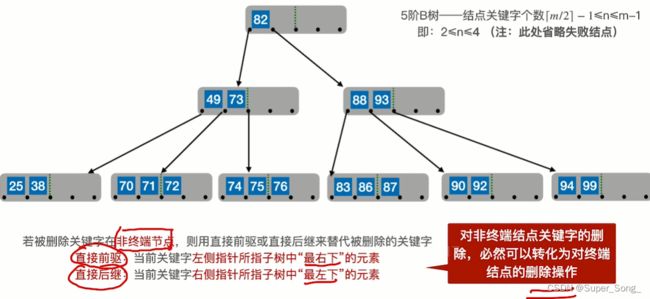
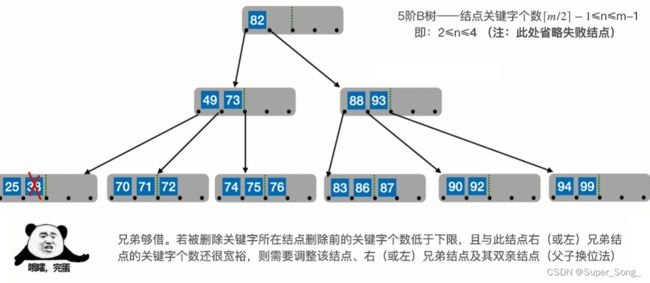
删除终端节点38,发现节点关键字个数不够了;分情况讨论
- 若兄弟够借,以升序为例,右兄弟贡献最左侧的,左兄弟贡献最右侧的;
- 父节点贡献关键字给下边不足的结点,兄弟贡献的关键字再给父节点补上
- 注意时刻确保结点关键字符合B树的规则
- 这里就是,父节点49补下来,右兄弟70顶上去
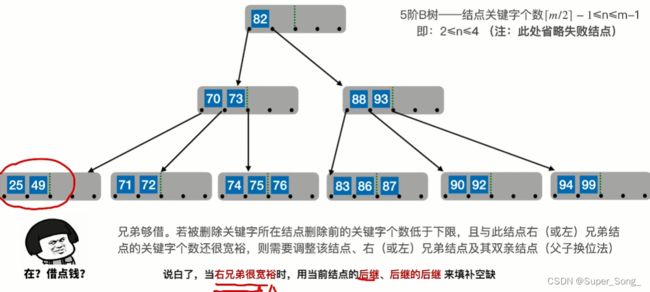
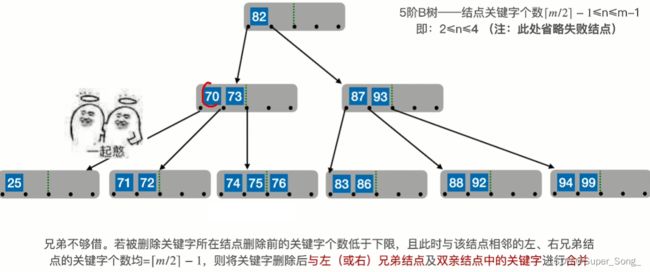
删除90,结点关键字不足;找左兄弟借关键字 - 当前节点的前驱是88,前驱的前驱是87
- 88下来,87顶上去
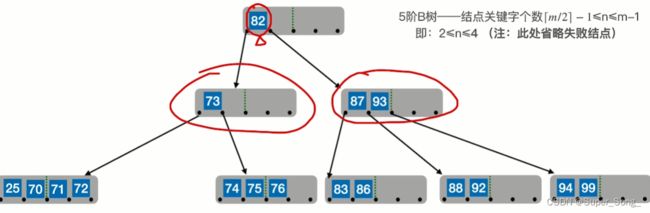
- 两个结点合体,还要把这两个结点的中间的结点70拉下来,一起合体
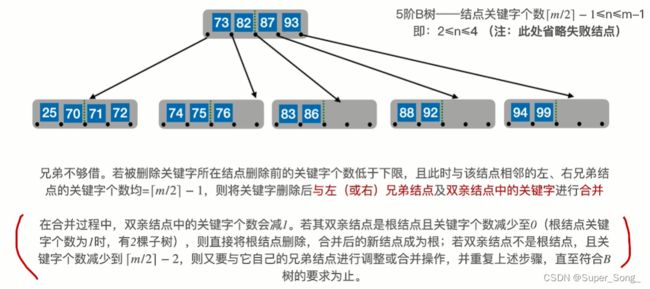
- 父节点和右兄弟合体,同时把父节关键字82点拉下来;
- 旧的根结点删除
- 注意核心要求
- 实际不可能再出比5阶更难的B树
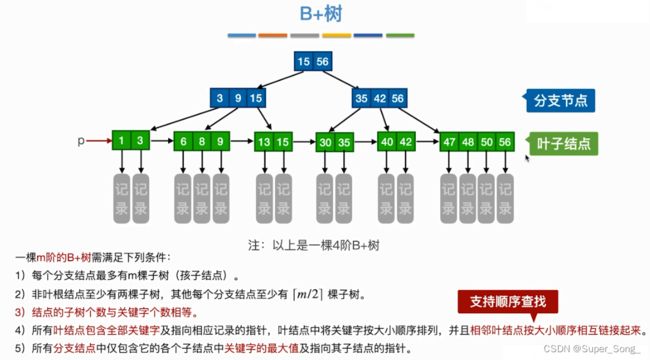
B+树
概念
- 考试一般不会太深,主要考察概念性的知识,且容易伴随着B树对比着考察
- B+树的数据结构类似于分块查找
- 通常把最下面的一层的结点,成为叶子结点
- 所有的叶子节点包含的所有关键字就是全部的元素
- 非叶子节点中的关键字,表示的是自己所负责的区间内的最大的元素
- 非叶根节点:不是叶子结点的根节点
- 因此,从叶子节点的起始点向后遍历,也能得到所有元素,支持顺序查找
- 这里的叶子结点指的是一整块结点,里面可能包含多个元素
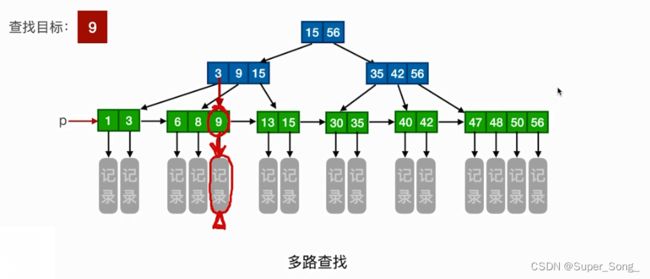
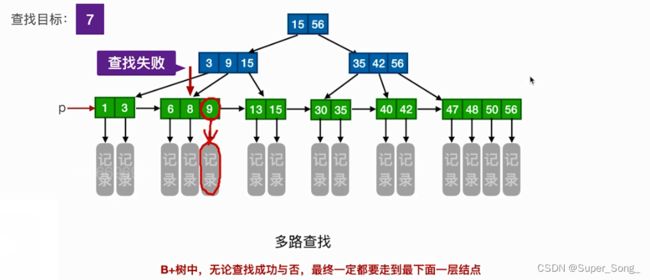
- 看查找的元素值落在结点的哪个关键字所负责的区间里
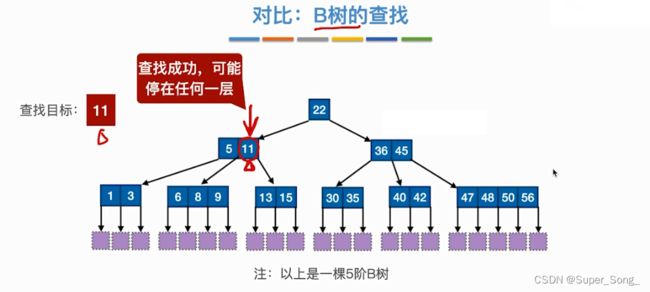
- 如果在非叶子节点找到了关键字值相等,也不要停,继续找到叶子节点,因为信息都存在叶子节点内
- 可能停在任意一层,就查找成功了
- 树的结点信息其实是存储在磁盘块中,系统将磁盘块读到内存的时间开销很大
- B+树的非叶子结点保存的信息更精简,使得一个磁盘块可以存更多的关键字,间接减少了切换读取磁盘块的次数,查找更快
- 每切换结点查找的时候,其实都要切换磁盘
- 磁盘块的大小固定的,所以关键字越小,磁盘块就能存的越多
- 结点的关键字越多,分支就越多,树的阶就越大,树就越矮
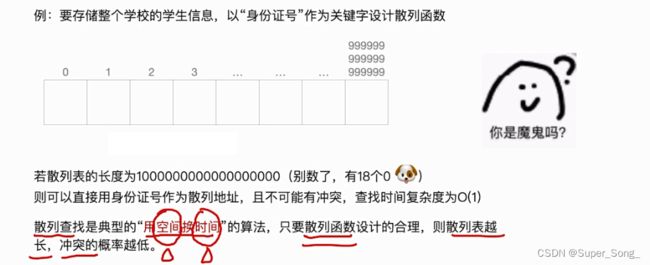
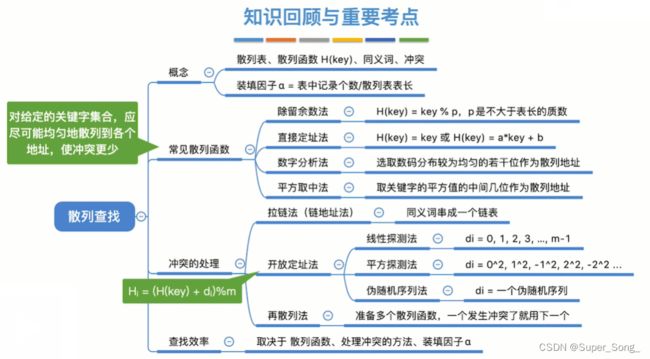
散列查找
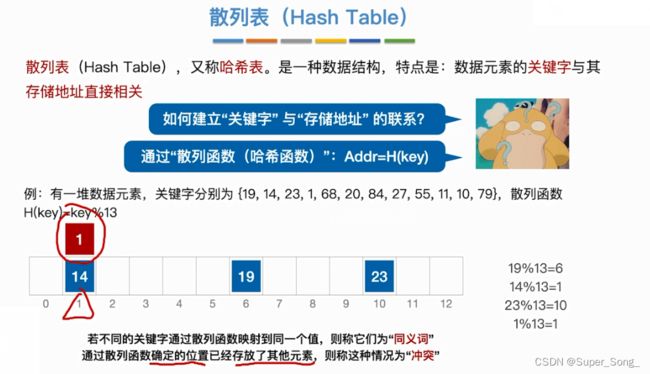
散列表 Hash Table
- 散列表,散列函数,哈希表,哈希函数,都是同一个东西
- 哈希函数是人为设计的,根据不同需要可能定义的函数不一样;
- 归根到底就是为了将关键字的值映射到指定的存储地址上
- 同义词,冲突
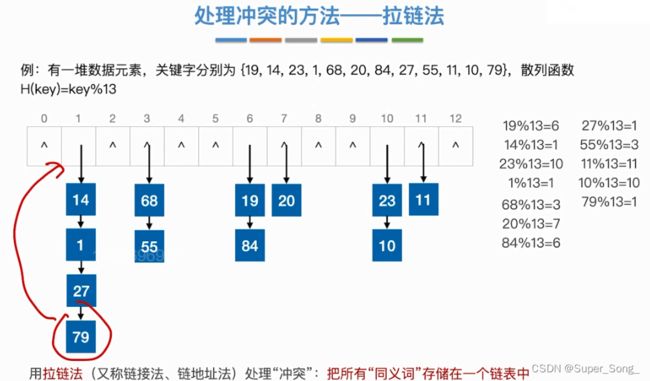
- 数组不再存储关键字,而是保存关键字的指针
- 遇到有冲突的关键字,直接在冲突的关键字上连接指针
- 指针是前插还是后插先不必纠结
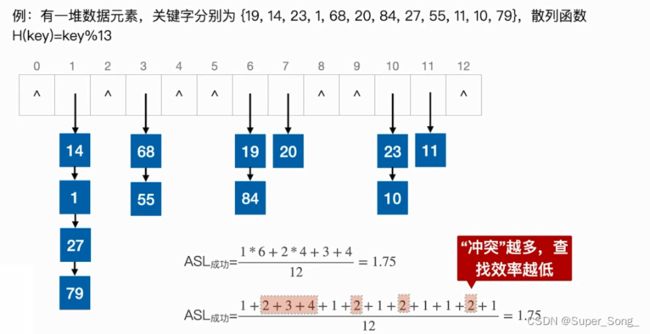
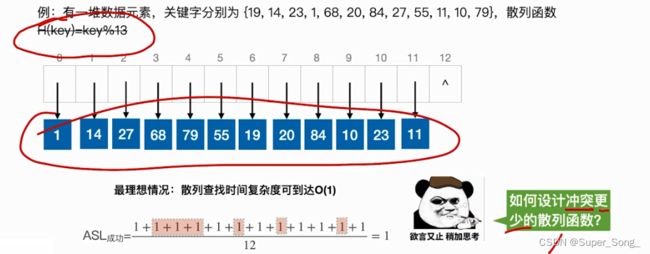
- 散列表设计的足够大,没有出现同义词,则查找的时间复杂度为O(1)
- 假设,关键字映射到各个坑位的概率相等
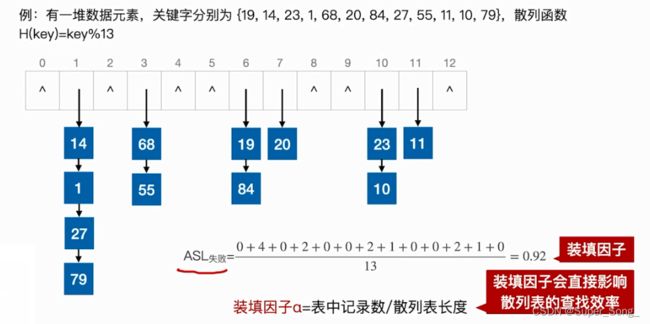
- 查找失败的平均查找长度,其实也叫装填因子
- 装填因子表示散列表装的有多满,越大则越满,越满则越容易出现冲突
- 这里主要介绍常见的散列函数
除留余法
- 为什么取得是质数?为了让不同的关键字尽可能减少冲突
- 余数,可以自己是试试
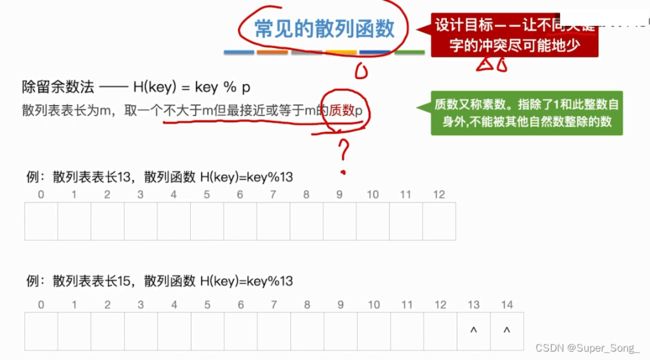
如果给出的关键字是连续的,看起来取得数是不是质数没什么影响
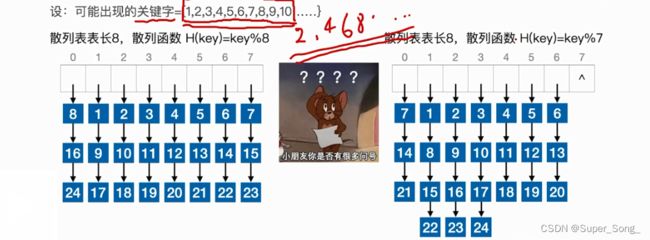
如果关键字都是偶数,或者有一些公约数的时候,取质数的优势就出来了,即使有个别位置浪费,也是划算的
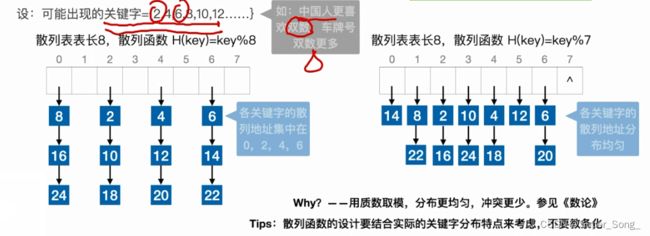
直接定址法

数字分析法
- 取分布均匀的一段数码位作为散列地址
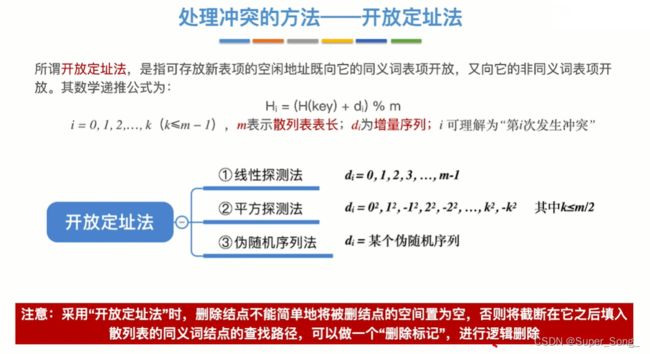
- 拉链法的数组里只存放元素指针,开放地址法的数组里可以用来存放元素
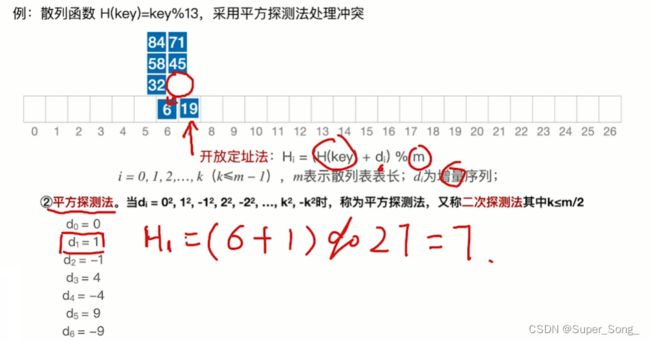
- 数学递推公式:原本哈希函数算出的地址,加上一个增量di,对散列表长取模
- 其实就是发生冲突的时候,不再存放原来的位置,而是基于原来的位置发生偏移
- 偏移量是多少,和当前是第几次冲突有关系
- 偏移量di的取法,可以有三种,线性探测法,平方探测法,伪随机序列法
- 注意,经过线性探测之后,如果新的位置发生冲突,还会根据新的地址,重新探测

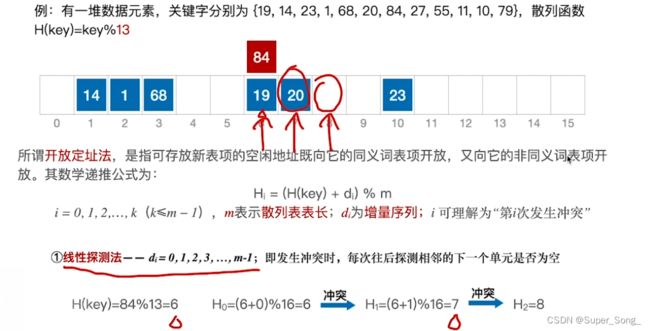

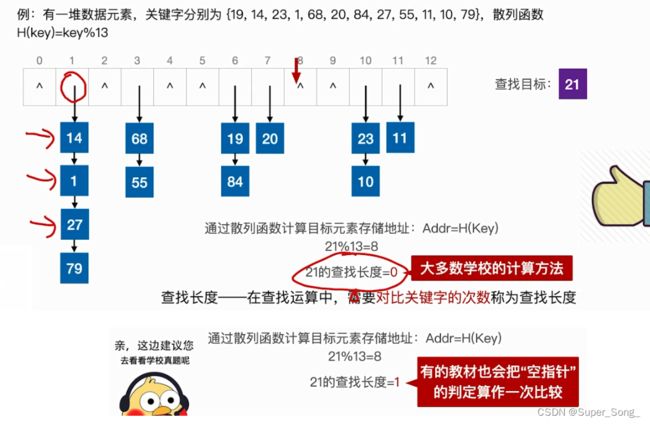
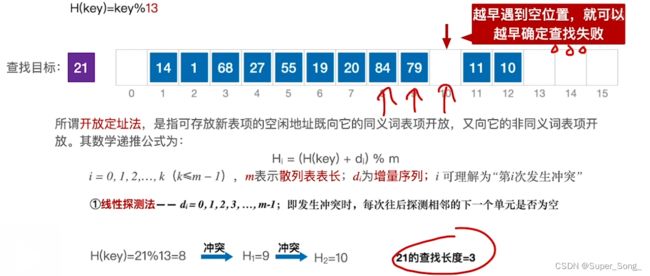
取模长度 - 哈希表长度16,小于16的质数为13,
- 不冲突的时候,是对13取模;冲突时,采用线性探测,偏移量是对表长16取模
- 这么做也是为了能充分利用地址
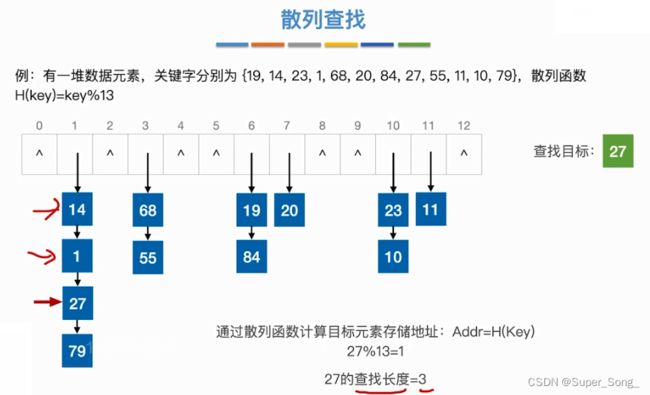
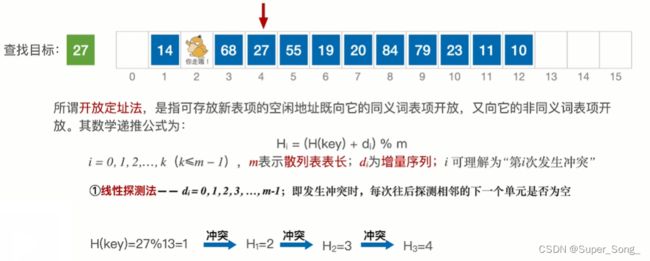
- 找到的元素与查找目标不等其实就是冲突
- 按照偏移规则,找下个位置,再比较;直到元素与查找目标相等,就是查找成功
- 本例中,找到27之前,查找了14 1 68,其中14和1与27是同义词,14和68不是同义词
- 同义词和非同义词都会被检查到,这是因为偏移导致的
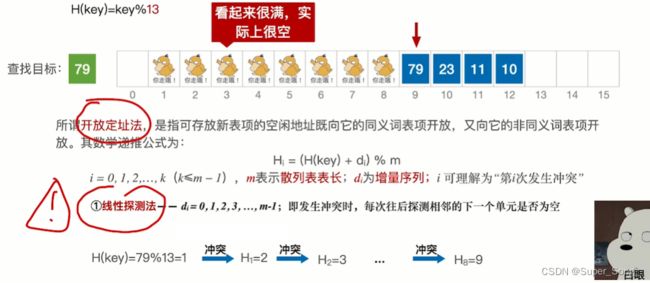
- 注意,对空位置的探测也算作一次查找;这里要和拉链法区别
- 为什么?因为拉链法数组里不保存元素,而开放地址法的数组里保存元素,
- 越早遇到空位置,越早确定查找失败
- 不能单纯的删除某一元素,否则后续的元素查找并偏移经过这里时,会被截断,因为这里时空,误认为查找失败
- 使用标记,表示这里已删除;其他查找经过这里时,不影响偏移
- 开放地址法弊端:删除过的元素较多时,会导致查找长度变长
- 成功
- 失败:初次探测的地址是对13取余得来的,所以只能是0-12,所以我们规定初次探测落到0-12的概率都是1/13
- 因此,查一个元素,如果初探落在0号位,直接失败;初探落在1号,要一直偏移到13号位置,才能失败;以此类推


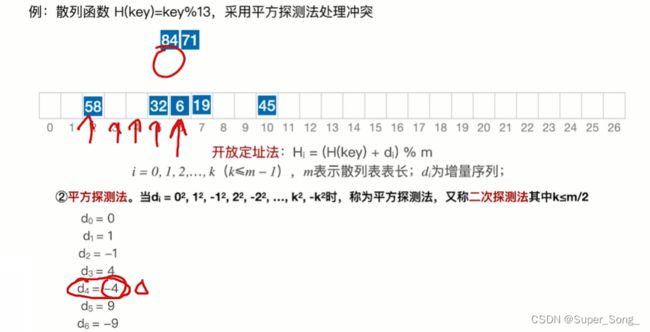
平方探测法 - 其实就是有原来的冲突次数di,变成了±冲突次数平方
- 6正常放入;
- 19对7取余,冲突;开始偏移,偏移时对表长27取余;
- 比起线性探测法,平方探测法更不容易出现堆积
- 散列表长度必须可以表示成4j+3的时候,才能探测到所有位置;
- 为什么,可以亲自试一试,记住结论就好,原理在《数论》里
- 增量序列,改为一个伪随机序列,其余相似
- 以严慰敏为主,王道书的解释有问题
第八章 排序
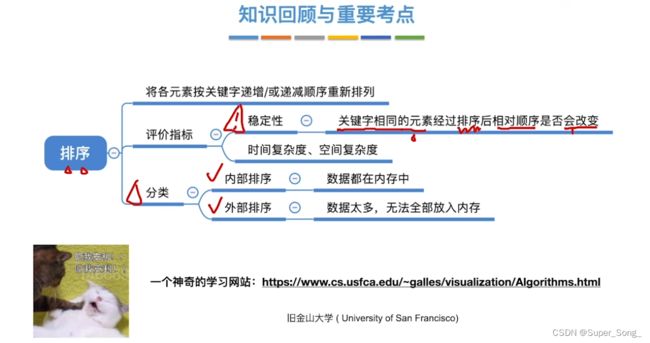
排序–基本概念
什么是排序
重新排列元素,使其关键字有序,递增或递减,难免会到关键字相同的情况
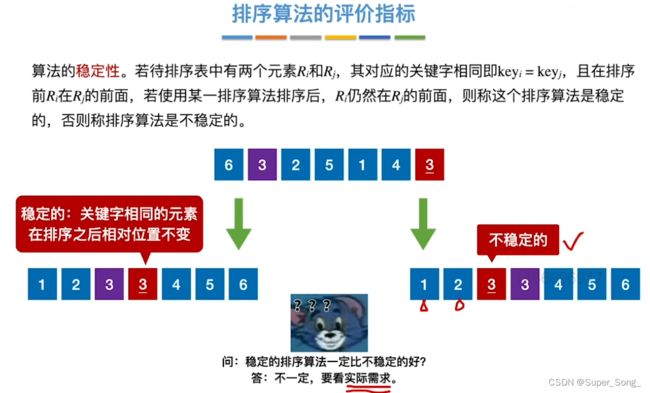
排序算法的评价指标
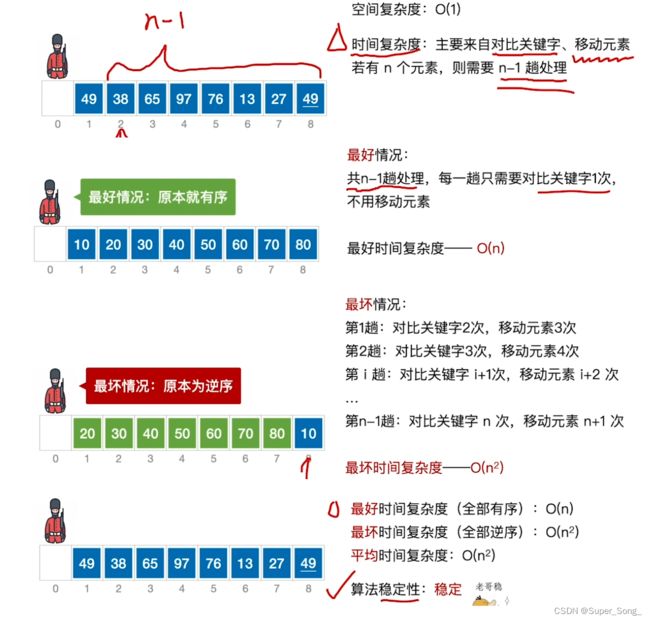
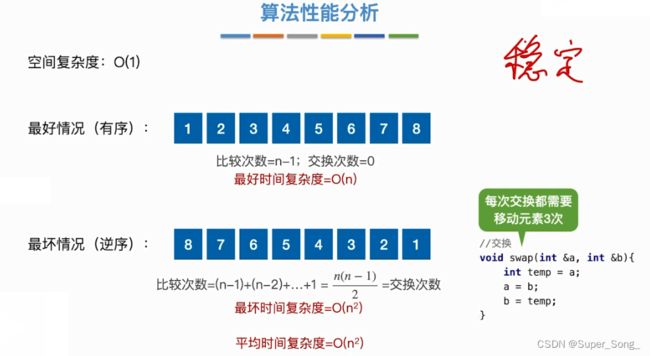
- 时间复杂度,空间复杂度
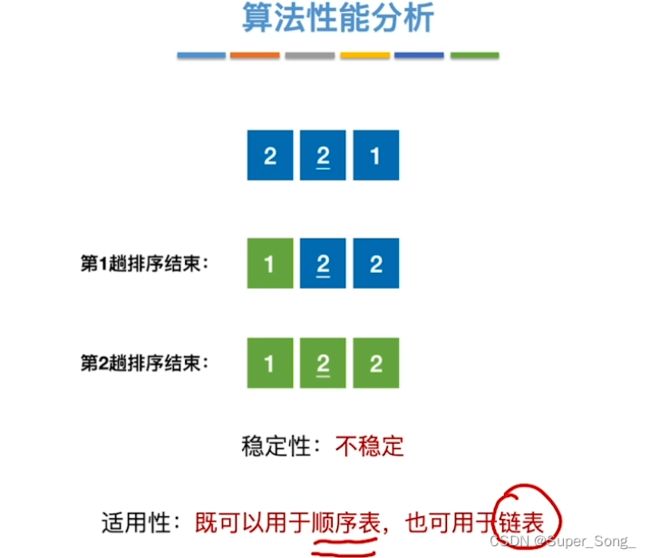
- 两个关键字值相同的元素,在排序之后,相对位置没有改变,排序算法就是稳定的;否则就是不稳定的;选择题常考
- 稳定的排序算法一定比不稳定好?结合需求看,看需不需要;如果本来就不可能出现关键字重复的情况,稳定与否也无所谓了
插入排序
算法思想
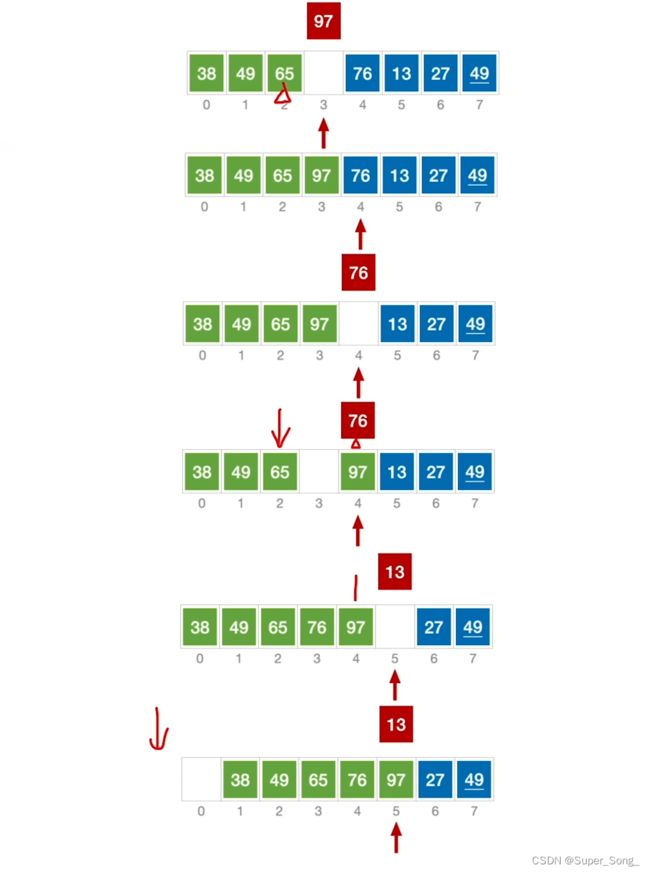
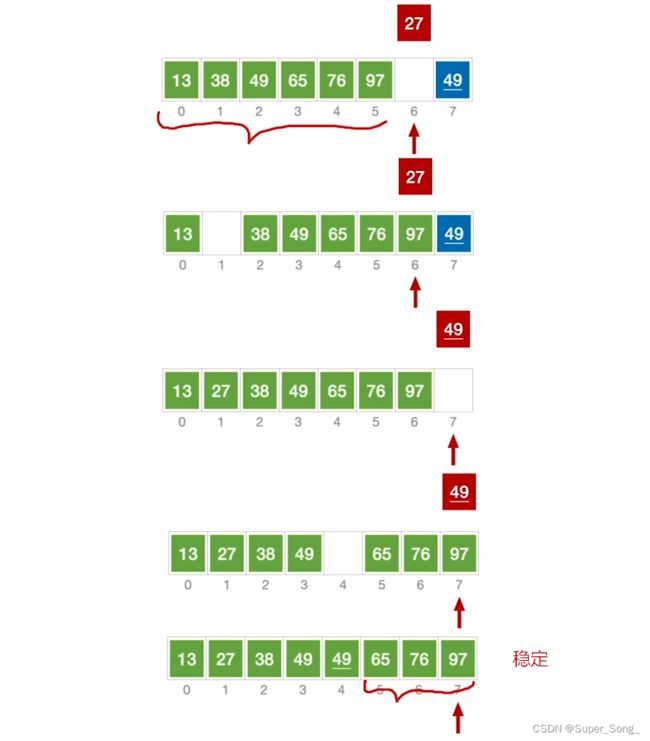
- 每次将一个待排序的记录,按其关键字大小插入到前面已经拍好的子序列中,知道全部插入完成
- 自行看动画
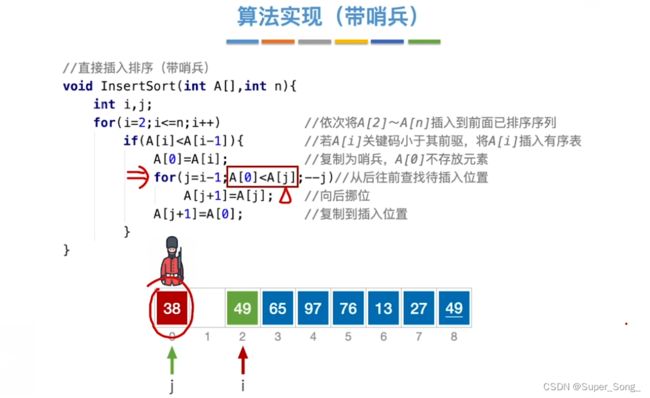
- 从编号1,即第2个元素开始往前插入;0号元素,假定他就是排好序的子序列;
- 与前面的本质一样,只是改为由0号位保存临时元素
- 前面的是通过j>=0 && a[j]>temp 结束内层循环;带哨兵的, 通过一个a[0]
- 咸鱼推荐前面的,因为思路清晰,更好理解记忆
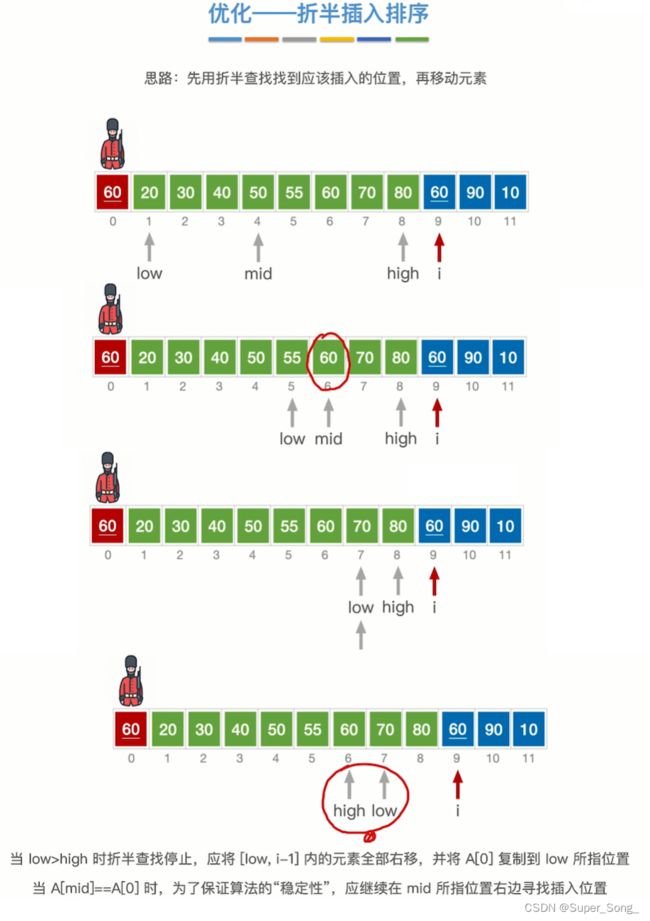
- 对前面已经排好序的子序列进行折半,用mid跟待插入的数据比较;然后进一步决定找mid左边,还是右边
- 当出现low>high,此时从low开始向右平移,待插入元素放在原来low的位置上
- 当出现子序列中有元素和待插入元素相等时,原本的插入排序停止比较,直接插入;
- 在折半优化中,为了保证插入的稳定性,待插入元素应该插到相等元素的右侧,所以此时折半不能停,还要继续
- 直到出现low>high时,并插入到相等元素的右侧
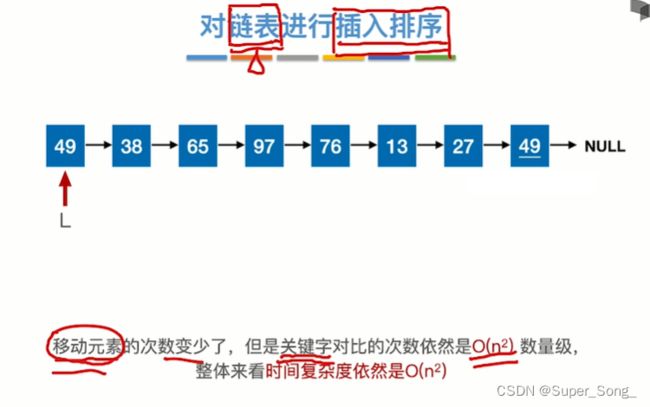
- 只是较少了关键字的比较次数,插入时,移动元素的次数没有发生改变,时间复杂度没有减少
- 移动元素的次数变少了;但是还是要顺序的一次对比关键字,所以时间复杂度还是没有改变
希尔排序
希尔排序
- 插入排序:如果原本就是有序的或者部分有序,使用插入排序就会效率很高
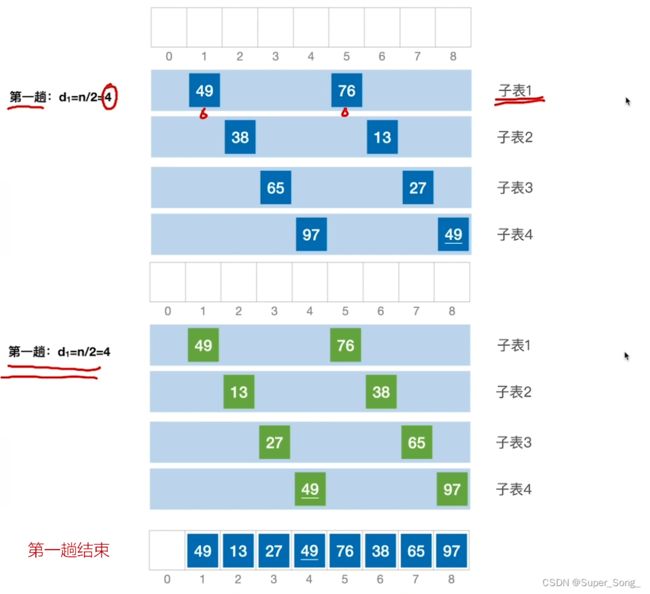
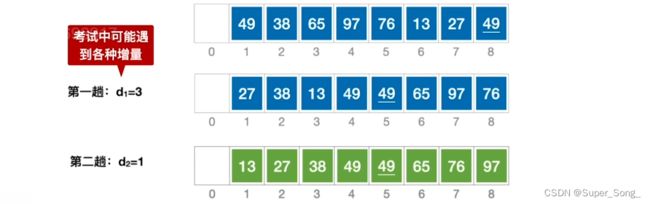
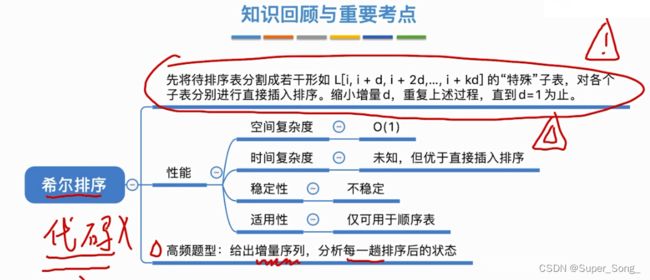
- 希尔排序:将待排序表分割成若干个子表,将每个子表进行插入排序,间接使得整体表变得更加有序
- 如何分割子表?从第一个元素开始,每间隔d取一个元素,收集成一个子表;再从第二元素开始,以此类推,收集成子表;直到所有元素都有了自己的子表
- 所有的子表是相互交错形成的大表,所以子表排序了,大表就会变得更加有序;
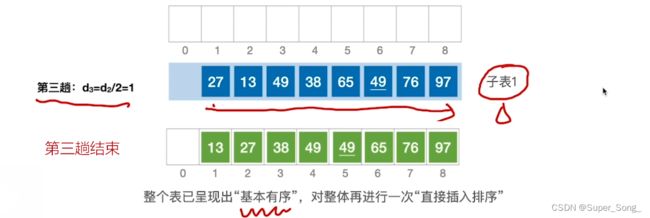
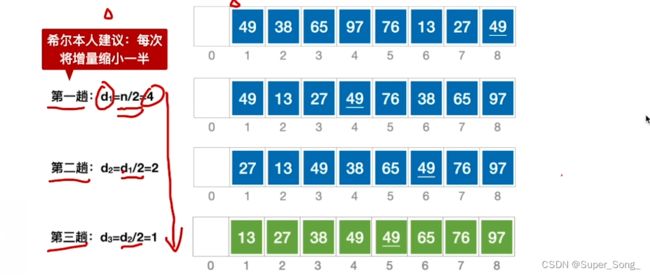
- 第一轮取d间隔;第二轮取d/2间隔;以此类推,直到最后,d=1,此时就会只有一个表,也就是对整体的插入排序;
- 希尔推荐每次d除以二,实际考试中,什么样的d都可能;
- 常考点:给定一组元素,规定d的值,问这一趟排序后,新的序列是多少
- 比较巧妙的地方在于,实现插入排序的时候是基于增量为d;
- 最外层循环是从d的维度进行的,表示第几趟,直到d=1,代表最后一轮的插入排序
- 第二层循环是从子表的维度进行,需要拿当前的元素和子表中的前面的元素一一比较,找可以插入的位置;有意思的是,这里的i++的过程,其实是各个子表再交替的进行插入排序,不理解可以看动画
- 第三层循环,即找到了可以插入的位置以后,待插入位置以后的元素依次后移让位置
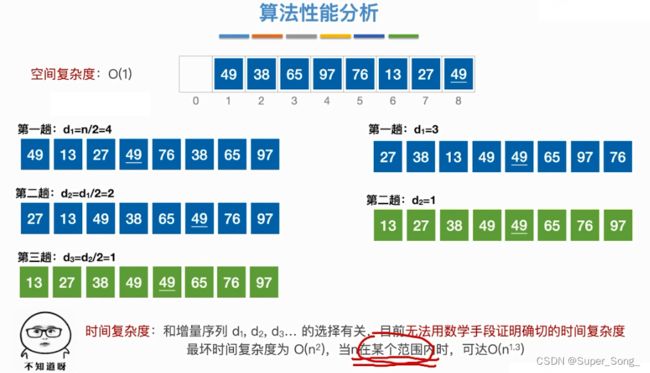
- 时间复杂度不确定,但通常比直接插入好一些
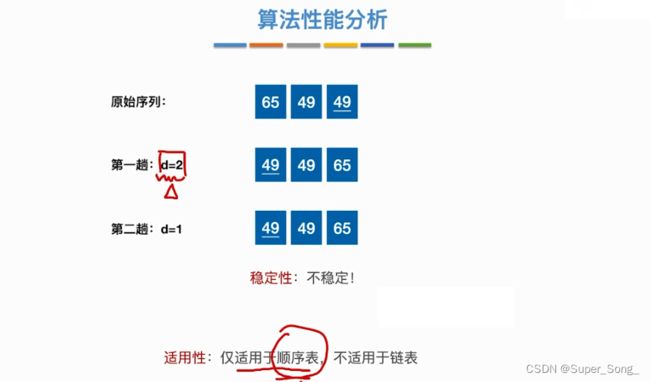
- 不稳定
- 仅适用于顺序表,因为希尔排序需要具有随机访问的能力
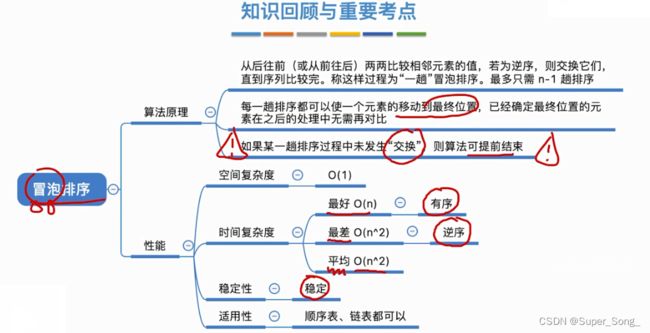
冒泡排序
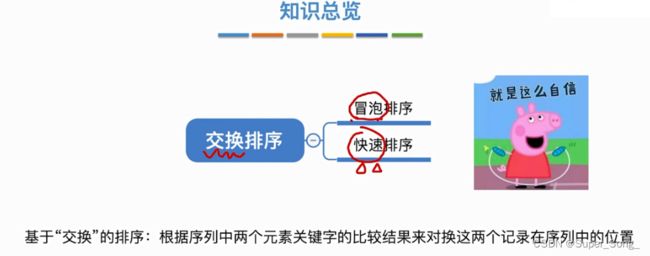
快速排序
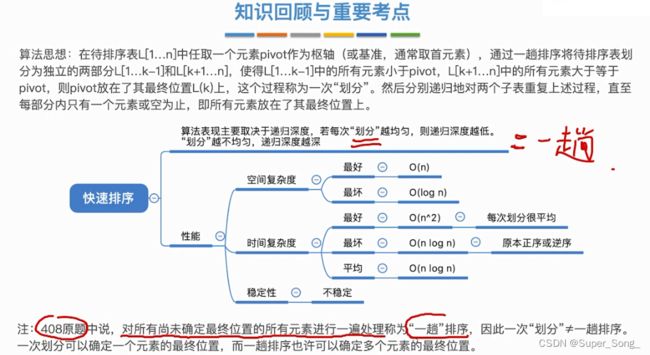
快速排序
- 是一种交换排序
- 是我们接触的内部排序中最优秀的排序算法
- 重要考点,考代码
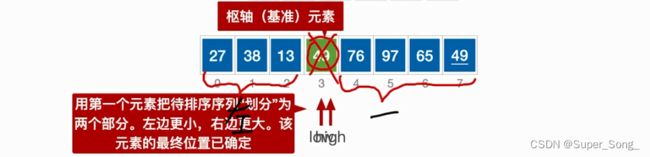
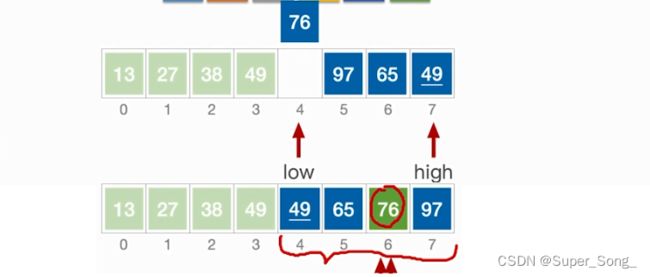
- 基于交换的排序:找一个基准,然后从首位两头开始,指针向中间移动,左边发现比基准达到就对丢到对面,右侧发现比基准小的,就丢到对面;
- 最终剩下的空位留给基准,这样基准左侧就是小的,基准右侧就是大的;这个过程叫一次划分
- 分别对左右两部分再进行地柜调用快速排序
- 通常选首元素作为基准
- low和high重合的剩余坑位就是基准元素的位置
- 一次划分确定了一个元素的位置;这个元素不用再管;
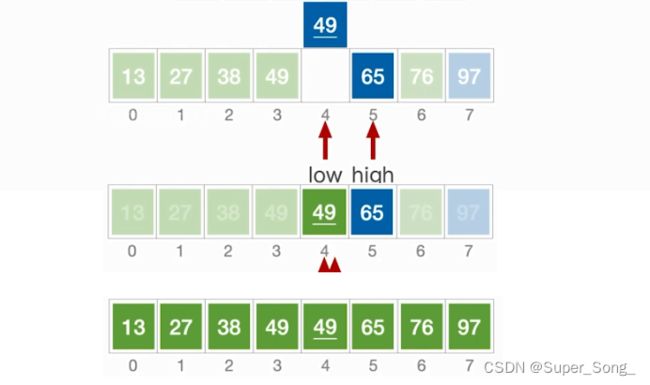
- 通过递归调用在对基准元素两边的两个子表进行分别划分,
- 直到子表中起始状态时low=high,其实就是子表只剩一个元素了,不需要再划分了
- quicksort中的判断,当出现low=high时,子表中只剩一个元素了,无需再划分了
- partition中的第一层while判断,是因为当low和high相互逼近到重合时,无需再逼近
- partition中的第二层的两个while判断,就是low和high不断向中间逼近的过程,直到找到一个比枢轴大或者小的元素,才能结束循环,并且把元素丢过去
- partition划分函数,返回的就是low和high重合的位置,即当前子表的枢轴应该放在的位置
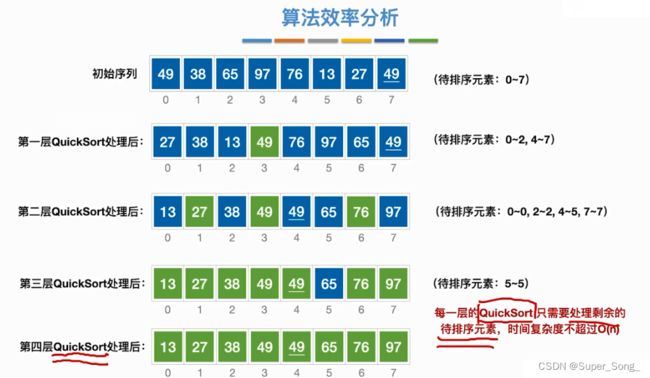
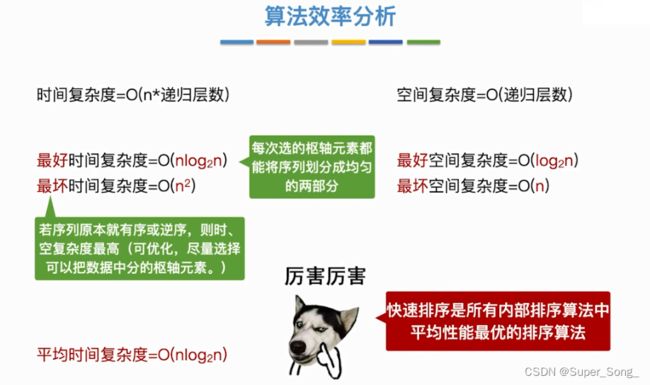
- 时间复杂度:每层不会超过O(n),总的调用次数与层数相关
- 空间复杂度:O(层数)
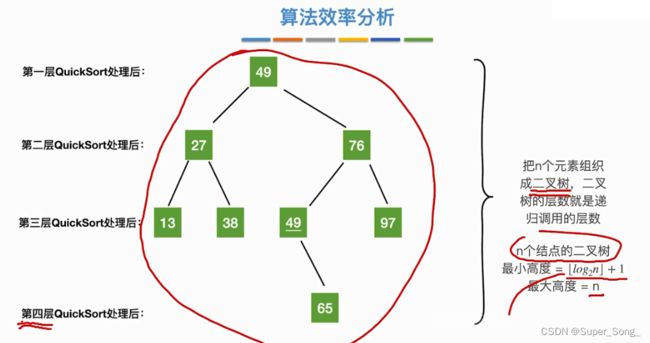
- 将每层调用分离出来,其实就是个二叉树
- 调用层数就是二叉树的高度;调用层数的范围就是二叉树的高度范围
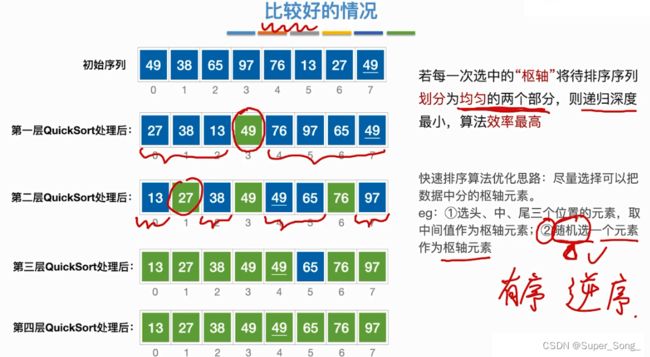
- 最好情况:每次枢轴都能将序列划分均匀,效率最高
- 最坏情况:如果序列本身就是有序的,就导致选中的枢轴总是在一端,大大增加了调用层数
- 优化思路:尽可能的选可以中分的枢轴元素
- 在实际应用,快排效率更加接近O(nlog2n)
- 因此,快排是内部排序中平均性能最优的排序算法
- 我们普遍认为的一趟排序,就是对某一子表进行一次划分,即调用了一次partation函数;所以一次划分,可以得出一个元素的最终位置
- 408原题认为的一趟排序,相当于图中的一层排序,要对所有元素都过一遍,里面可能包含多块划分,因而一趟排序可能会确定多个元素
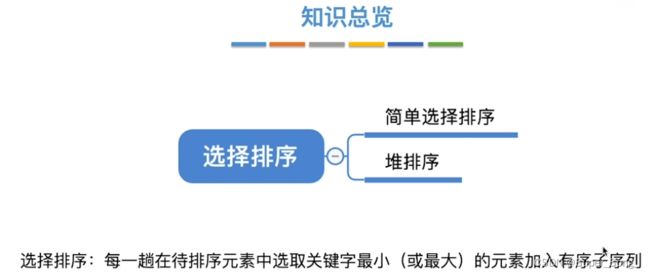
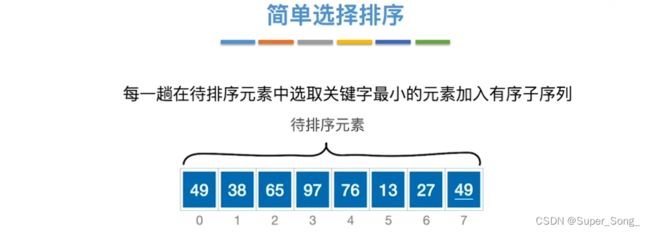
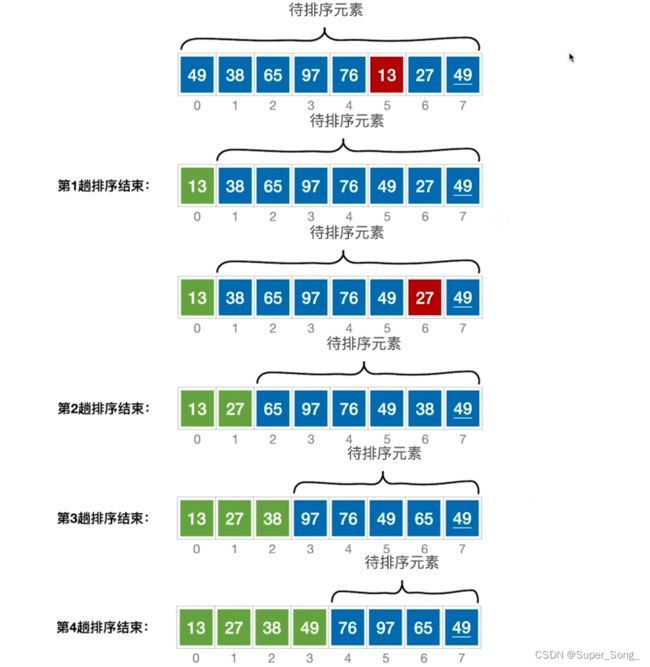
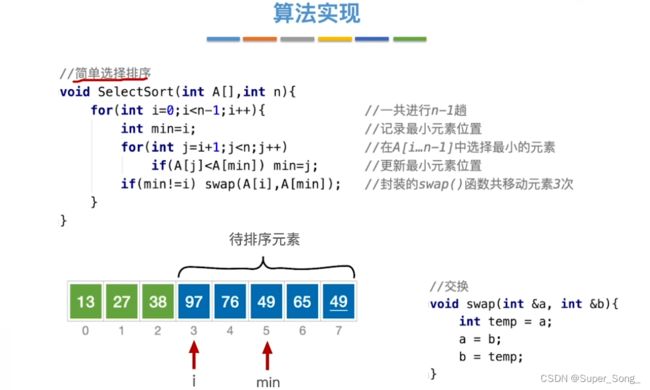
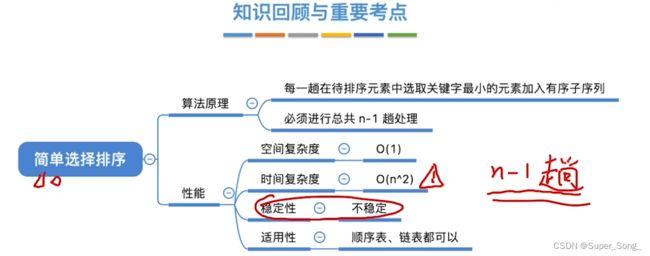
简单选择排序
- 与冒泡有一点相似,都是每一趟找出最小的,放到序列的一侧元素交换
- 区别在于,冒泡是两两的比较,简单选择排序是扫描整个待排序列,找出最小的
- 非常简单
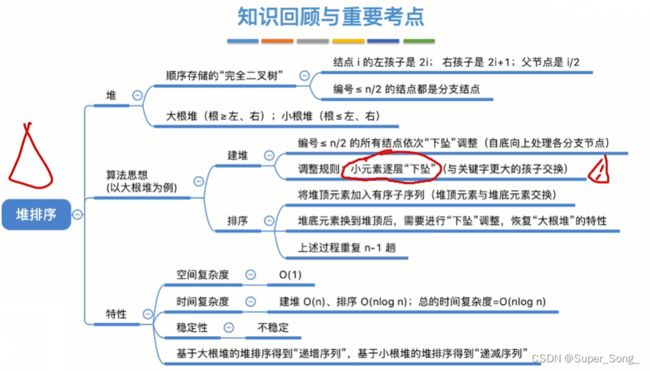
堆排序
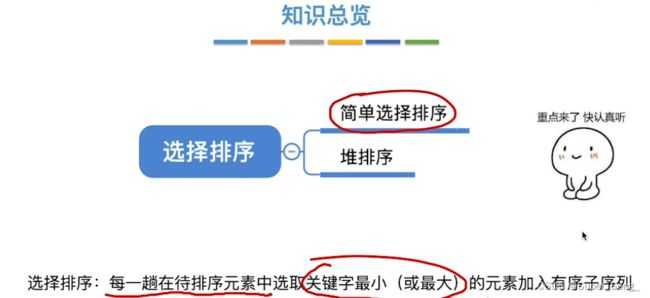
堆排序
- 选择排序的一种
- 难理解,又重要考点
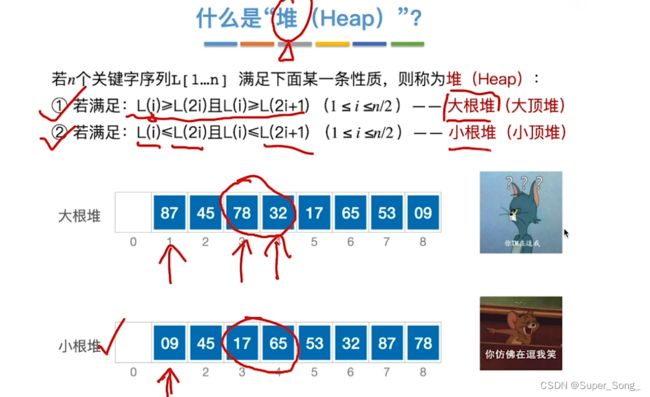
- 层序遍历建立的完全二叉树
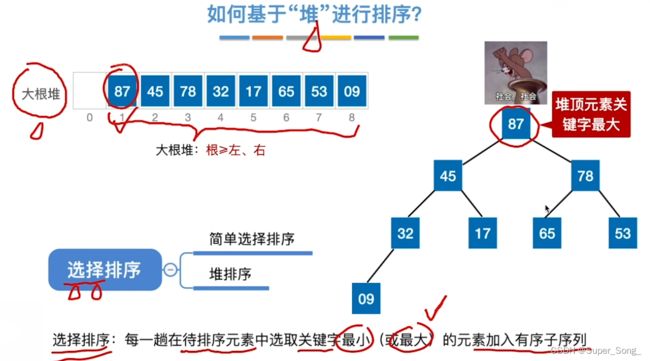
- 大根堆:完全二叉树的任意节点的值都大于左子树和右子树的值
- 小根堆:完全二叉树的任意节点的值都小于左子树和右子树的值
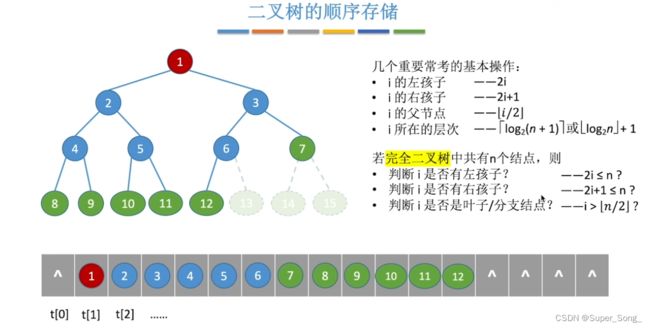
- 完全二叉树按照层寻遍历存储到顺序表中
- 父节点下标与子节点下标满足一定的数值关系
- 从存储视角看,大根堆是个连续的数组;从逻辑视角看,是个完全二叉树;
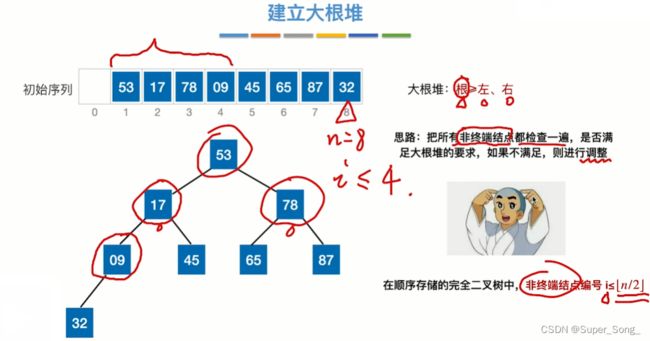
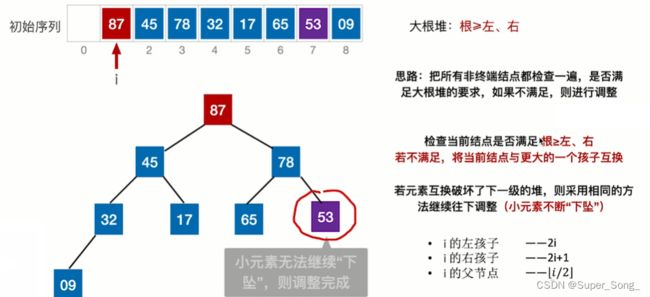
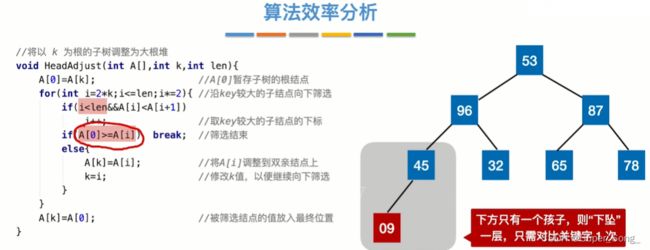
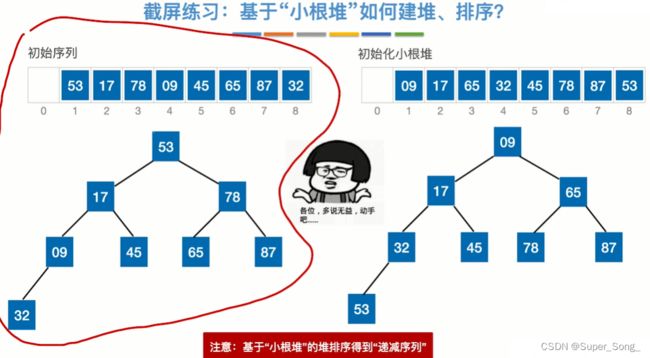
- 建立大根堆
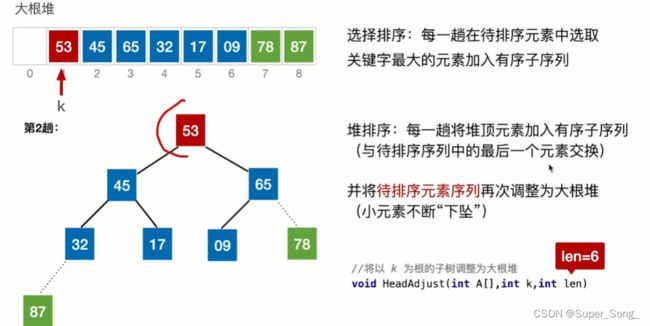
- 鉴于大根堆的特性,堆顶元素最大,取出最大元素,并存放到数组中;
- 重新维护大根堆的结构,再取出堆顶元素,存放到数组中;
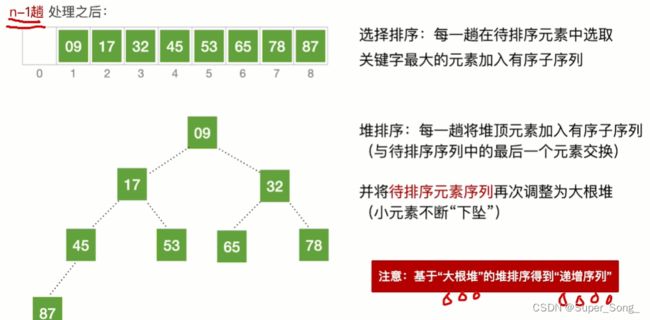
- 不断重复,最终得到的就是有序的数组
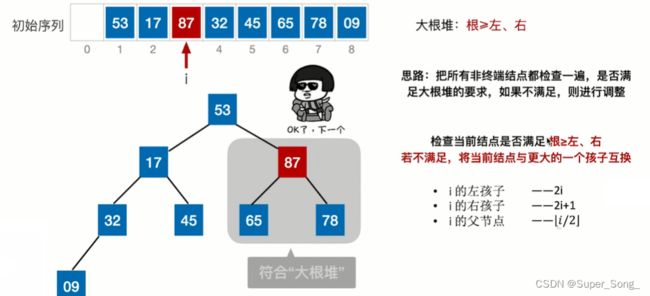
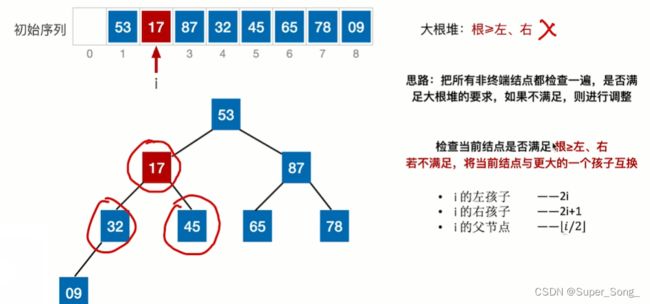
- 为什么是把所有非叶子结点检查一遍?
- 因为通过非叶子结点可以通过父子的编号关系找到所有叶子结点,即可以把所有的子树都比较一遍,不断的向上筛选出最大值,建立大根堆
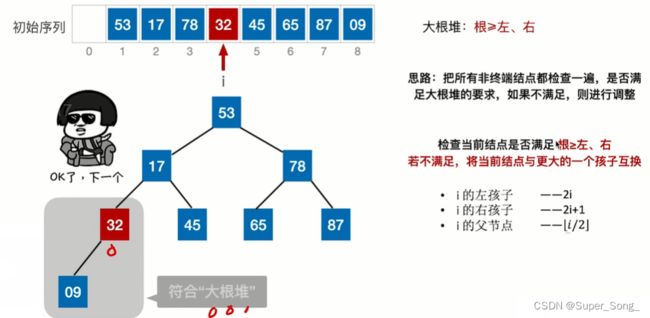
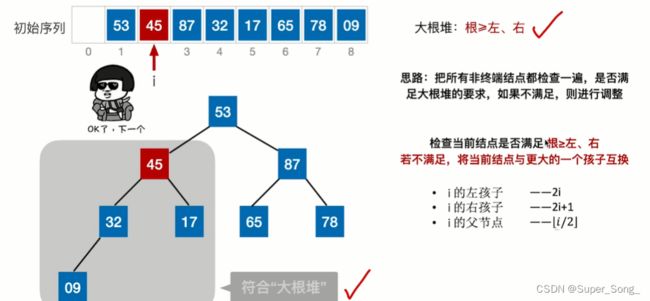
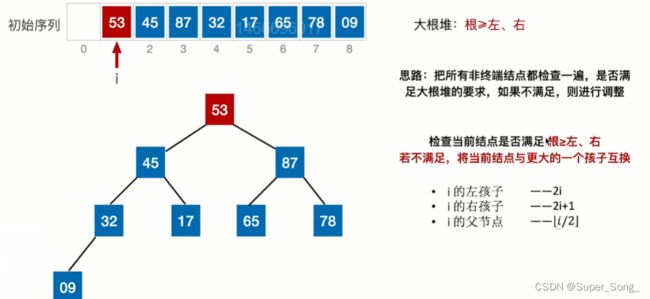
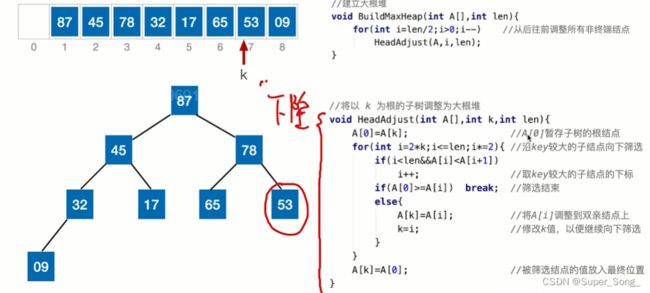
- 前面的调整省略
- 最后一步的调整,除了87升为堆顶;下沉的53还要继续下沉
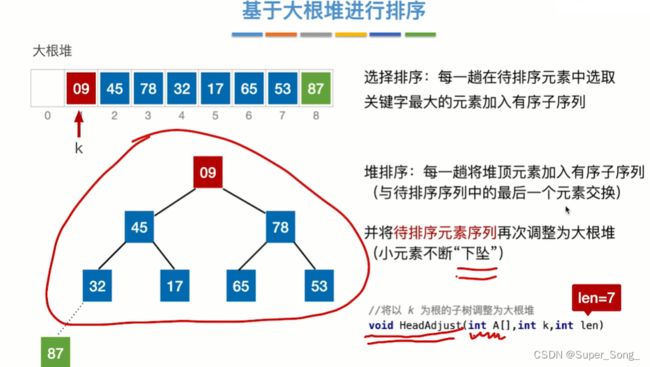
- 取出堆顶元素与堆底进行互换,这样堆底就是最大值
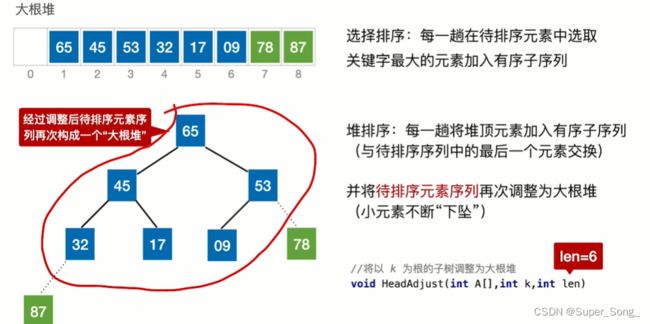
- 我们把堆底的后取出来的元素排除掉,剩余元素形成的新的堆,对这个堆进行维护
- 后面以此来类推
- 不断替换堆顶元素,形成新的堆
- 不断的从堆顶开始调整,下沉值小的元素,上浮值得大的元素
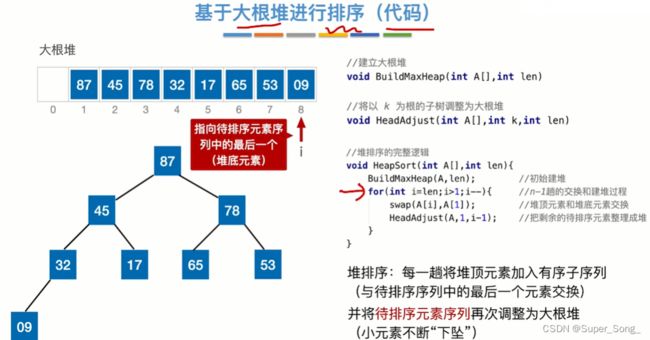
- 步骤:
- 1.建立大根堆
- 2.取出堆顶元素并保存到顺序表中
- 3.维护大根堆的结构
- 4.重复2-3步,直到大根堆中所有元素均保存到顺序表中
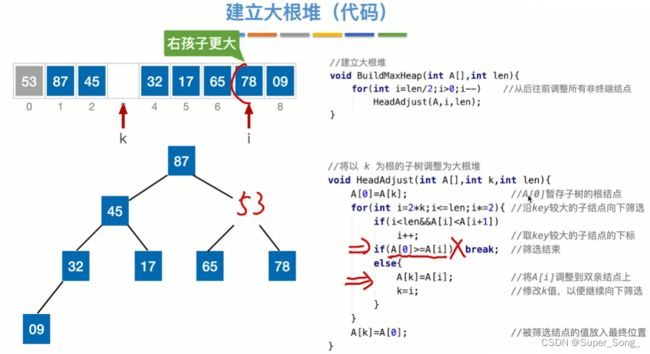
- 建立大根堆的过程:
- 从下标为n/2的元素,向前遍历,可以把所有的有孩子的子树都对比一遍,确保任意子树的父结点值最大
- 为什么从n/2开始?因为n/2的元素就可以找到n元素
- 建堆的过程更像是将树的最大值不断上浮到堆顶的过程,只不过是从n/2处出发,向1标位置遍历
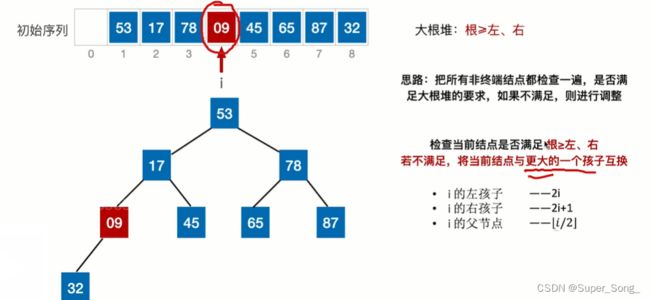
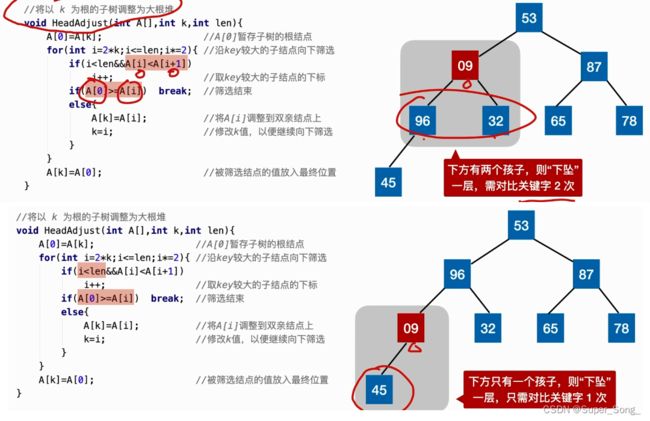
- 维护大根堆的过程:
- 从堆顶元素开始比较,如果左右孩子中有比堆顶大的元素,就和堆顶调换;
- 再分别对左右孩子下面的结点进行比较,让数值小的元素不断下沉
- 维护堆的过程也是将较大的值上浮的过程,只不过是从堆顶出发,不断的向子节点下标的位置遍历
- 调整函数既要将较大值上浮,又要将较小值下沉,并且是一直下沉到不能再沉为止
- 需要注意的是,这里的例子中,我们用来保存大根堆的数组是从下标1开始的,0标用来暂存
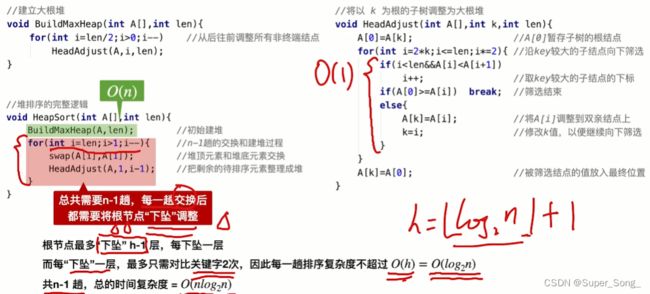
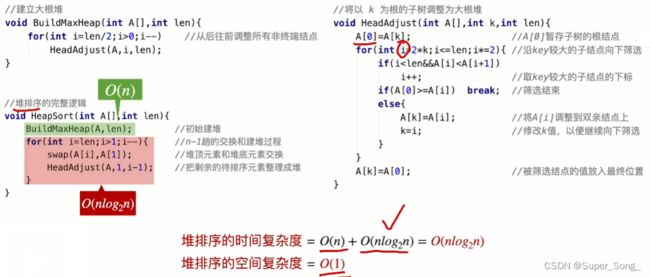
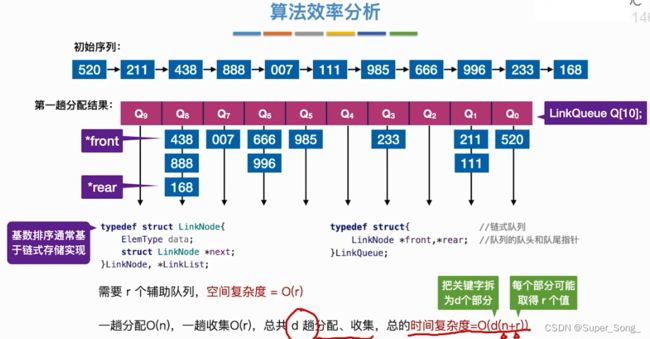
算法效率分析
- 重点在于分析下坠调整的函数
- 需要结合前面的二叉树的节点数,层数,树高之间的关系推导
- 能理解就理解,不能理解记住结论就好
- 建立堆的时间复杂度为O(n)
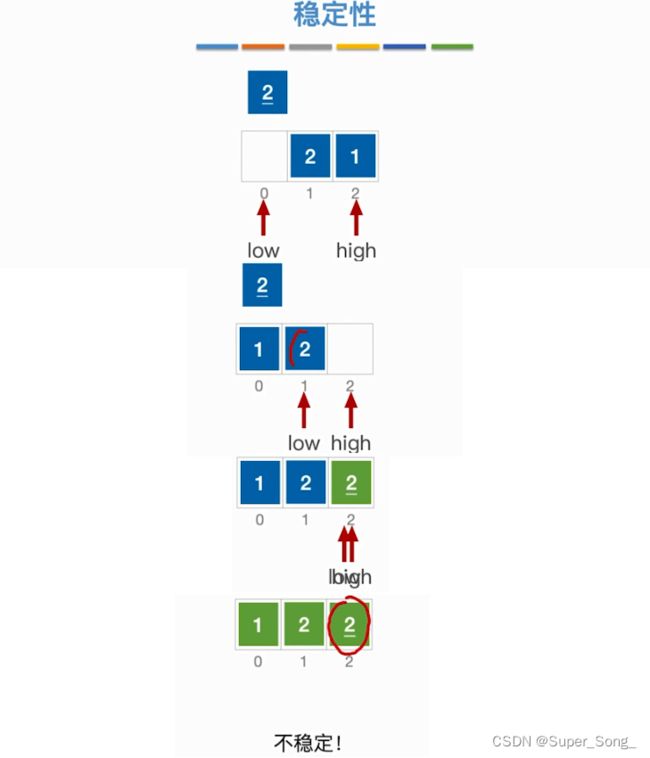
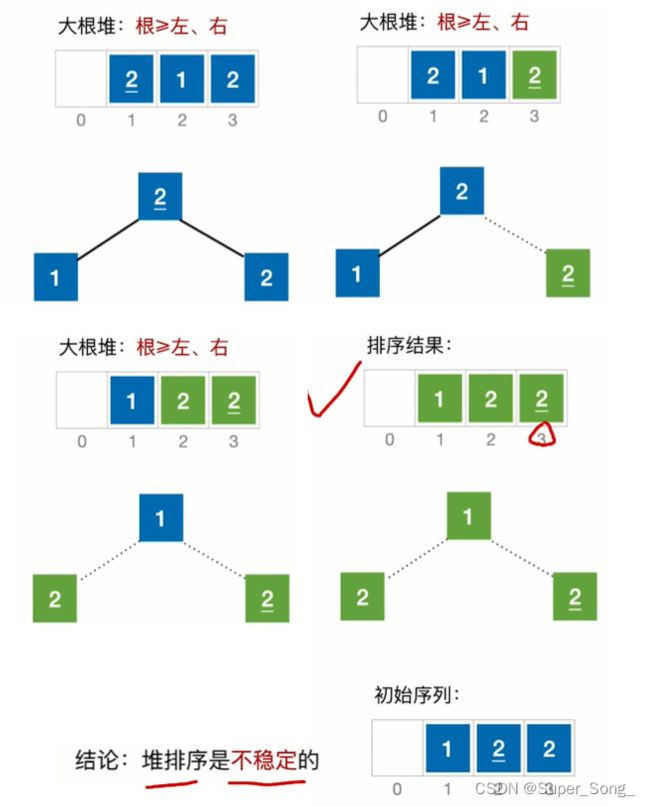
- 堆排序不稳定
堆–插入和删除
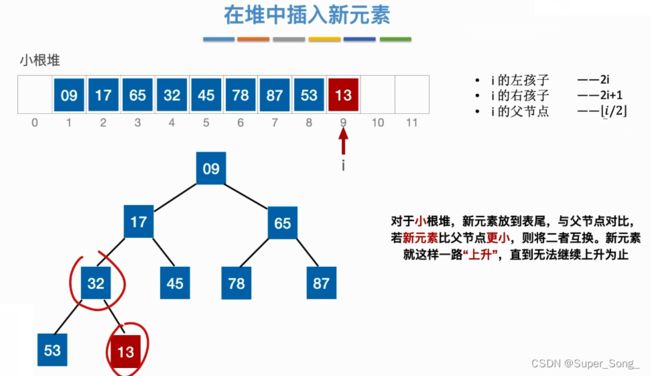
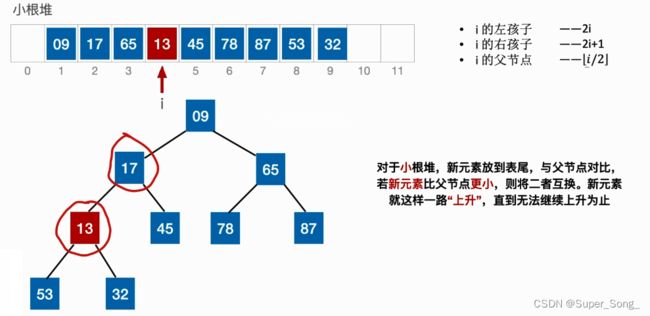
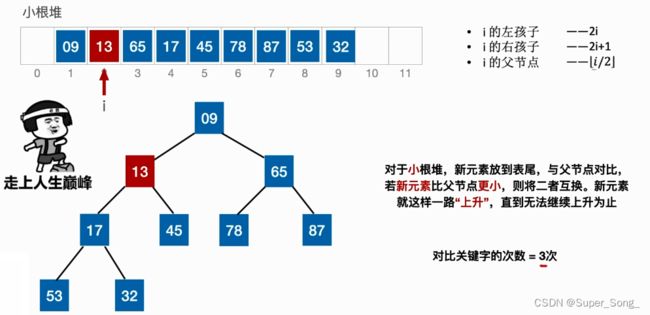
堆的插入
- 本案例以小根堆为例
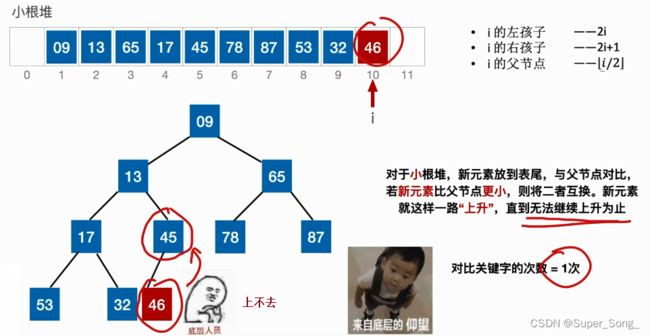
- 新插入的元素首先放在堆底,即表尾
- 找到插入元素的父节点比较,如果比父节点小,就和父节点调换
- 如果调换之后,在新的位置上再和父节点比较,不断上浮较小的元素
- 如果比父节点大,不用调换,则插入结束
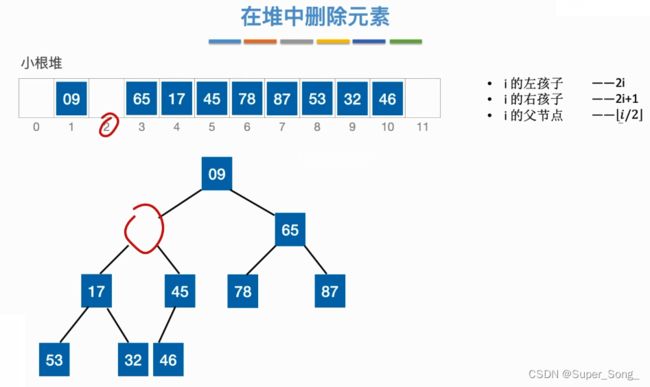
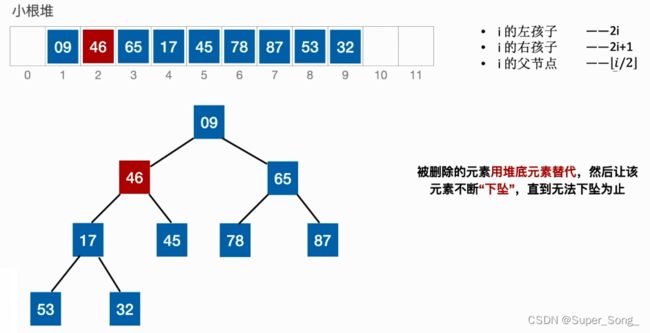
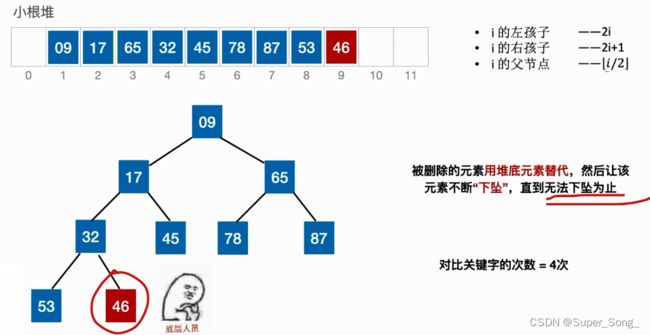
- 删除堆中的某一元素之后,用堆底的元素顶替被删除的位置
- 然后试图将这个元素下沉,跟左右孩子比较,找更小的孩子调换,如果比孩子都打,则删除结束
- 和更小的孩子调换之后,再新的位置上再和孩子比较,直到不能调换为止
- 为什么一开始从堆底顶替过来的时候不用跟父节点比较?因为父节点一定会比这里大
- 堆的插入和删除,考试常考对比次数
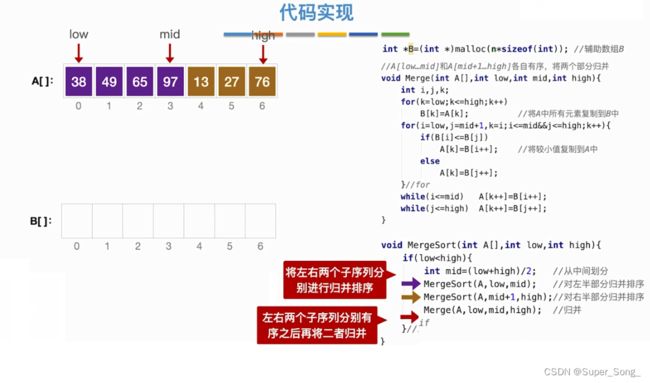
归并排序
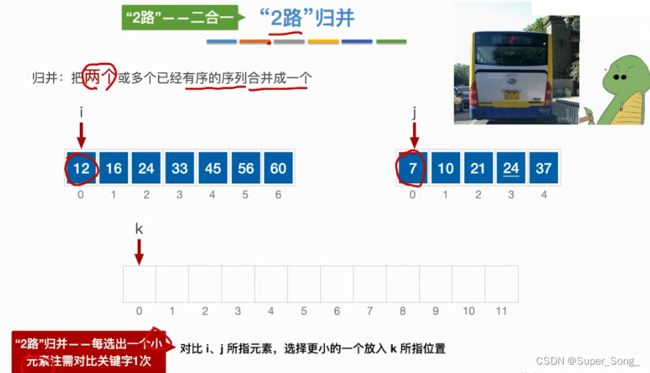
归并,合并
- 把两个或多个有序的序列合并成有序序列
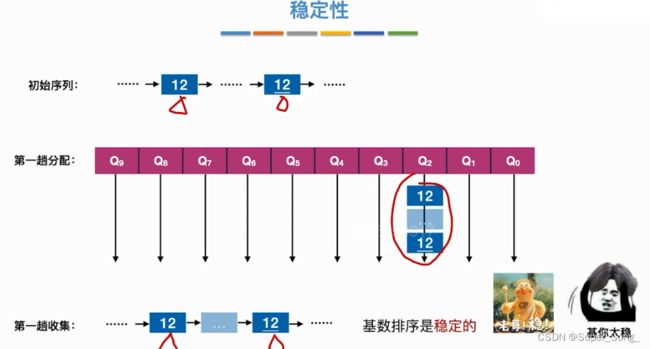
- 遇到相同元素的时候,我们定义规则,确保算法的稳定性


二路归并 - 把两个有序序列合并成一个有序序列
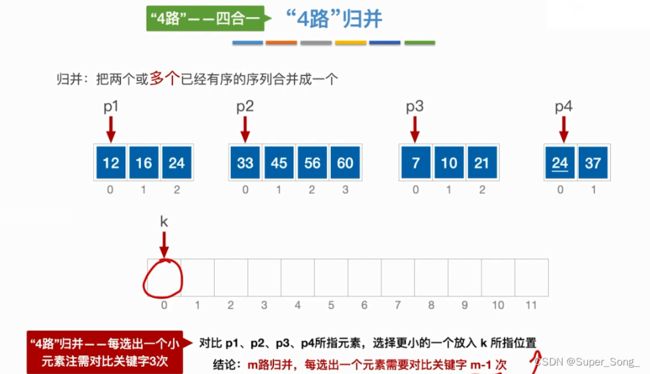
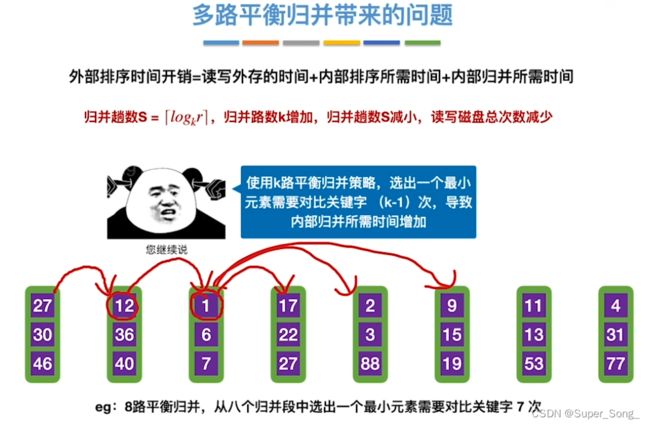
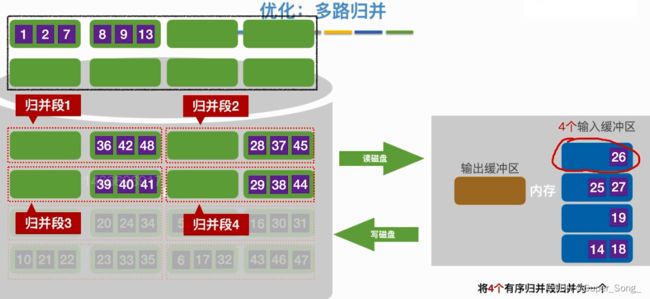
- 多路归并,类似
- 我们使用的归并排序使用的就是二路归并
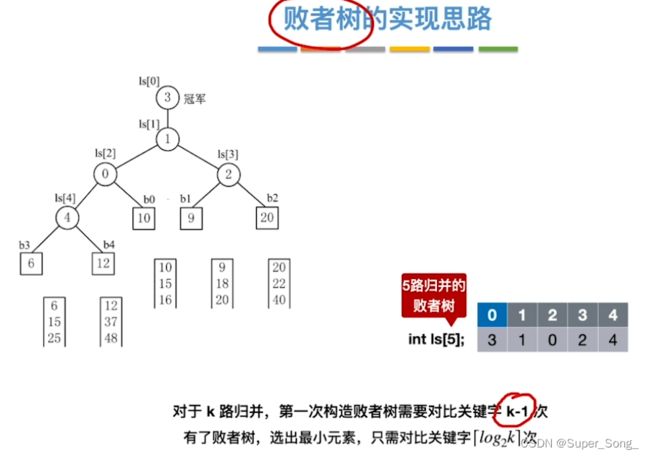
- n路归并,每次选出一个元素需要对比关键字n-1次;这里的二路归并就是1次
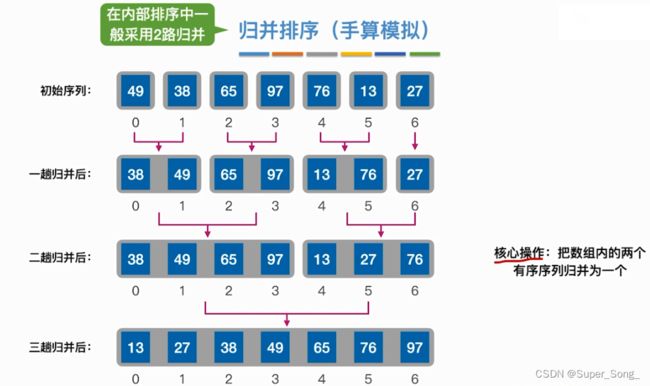
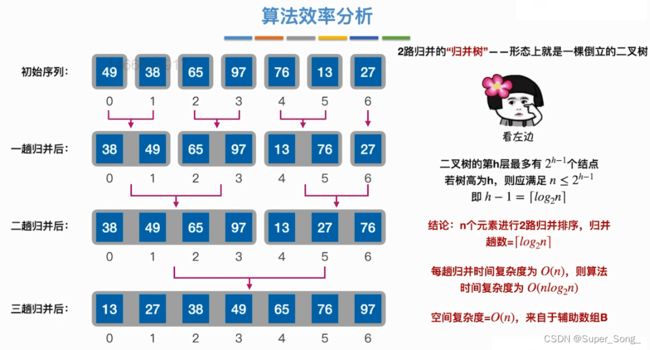
- 从紧挨着的单个元素开始两两合并,直至合成一个大的有序序列
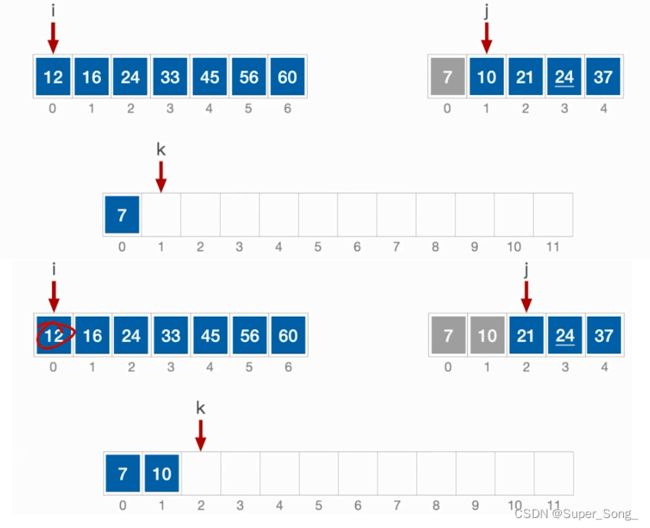
- 核心操作:将两个有序序列合并成一个有序序列
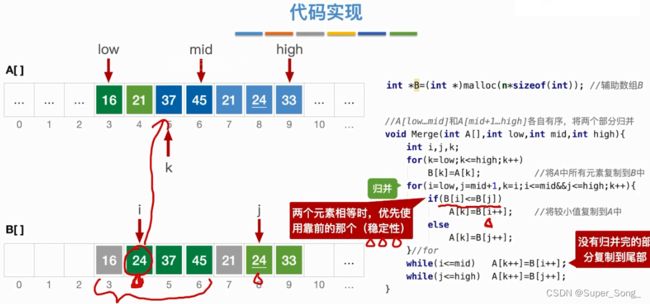
- 用low/mid/high来区分出两个子序列的范围
- 第一个for循环,用一个新的辅助数组临时保存两个子序列
- 第二个for循环,不断的从辅助数组中,取出两个子序列中较小的元素,并写入到原来的数组中
- 最后两个while循环,当其中一个序列没有元素后,另一个序列的元素全部保存到原数组中,无需再对比
- 遇到相等元素,优先复制靠前的那个,保证算法稳定性
- 将数组进行左右拆分,再归并
- 在归并排序函数中对左右两个部分进行递归调用归并排序,
- 实际上,递归调用的最底层就是相邻的两两元素进行归并,逐层返回,继续归并,最终整体归并完成
- 其中空间复杂度:包含辅助数组和递归调用栈,但是递归调用栈的不会超过递归的趟数,即log2n
- 所以空间复杂度最终还是根据辅助数组定,即O(n)
基数排序
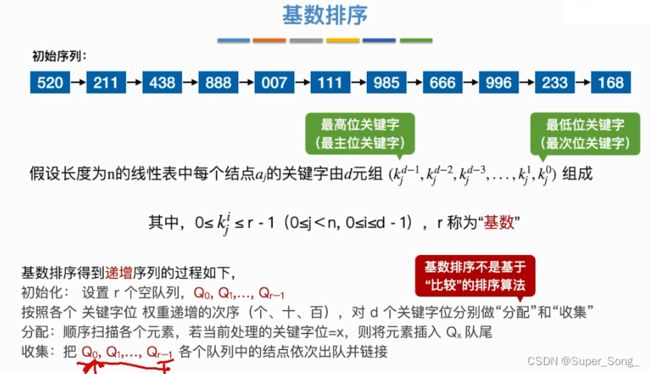
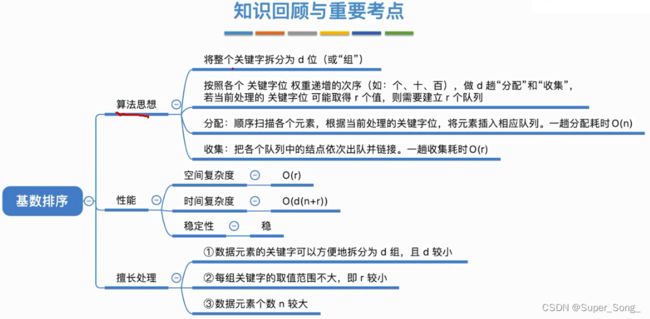
基数排序
- 之前的排序算法是基于比较进行的排序
- 基数排序跟之前不一样,比较神奇
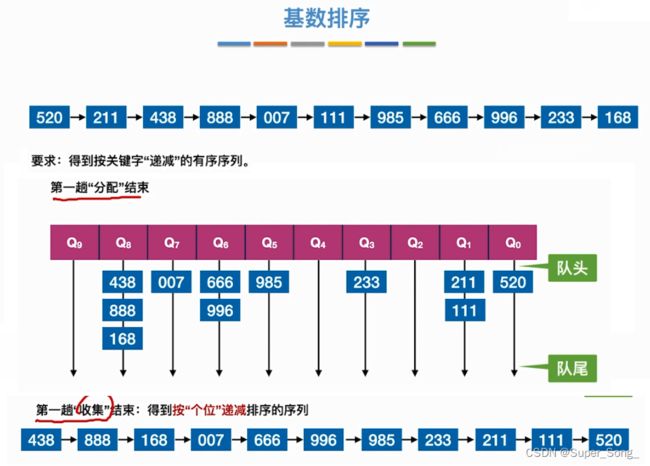
- 举例演示:
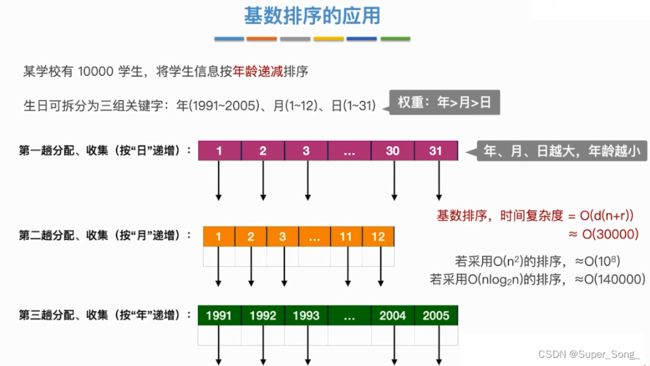
- 所有关键都可以拆分为个十百三个位,每一位的取值都为0-9十种情况
- 辅助队列由10个链表组成,分别容纳位数为0-9的情况
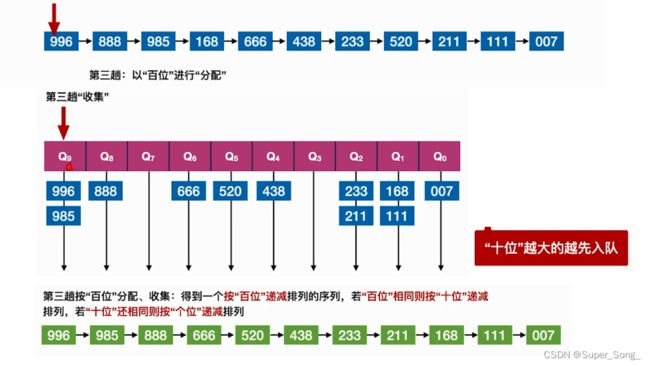
- 第一趟,按照个位的数字进行归类,完成后,再重新组成序列,此时的序列特点,个位数字大的靠前
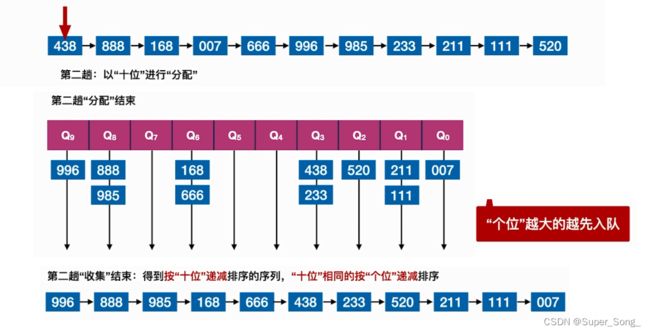
- 第二趟,基于上一个序列,按照十位数字进行归类,再重新组成序列,此时的序列,十数字大的靠前,在十位数字相同的基础上,个位数字大的靠前,
- 第三趟,以此类推,结果就是,百位大的最靠前,百位相同看十位,十位相同看个位
- 注意辅助队列中要保持先后顺序,队头的元素先收集回序列
- 以递减为例,递增同理
- 拆分组的方式,每组的各种情况,可以灵活变化;不只局限于个十百…的0-9
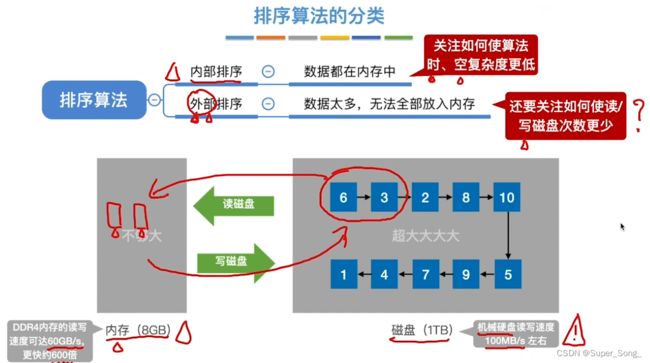
外部排序
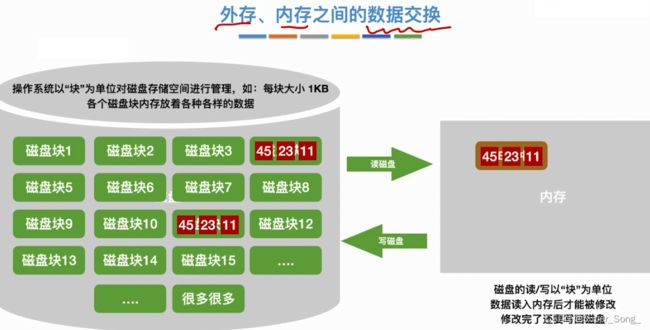
- 数据元素太多,无法一次全部读入内存,由操作系统分块存储在外存中
- 如何读取,修改?内存读一块,在内存中修改,再写入外存
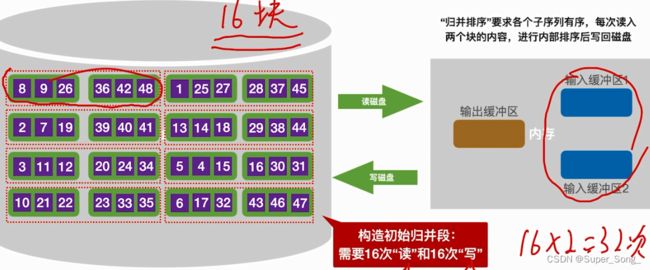
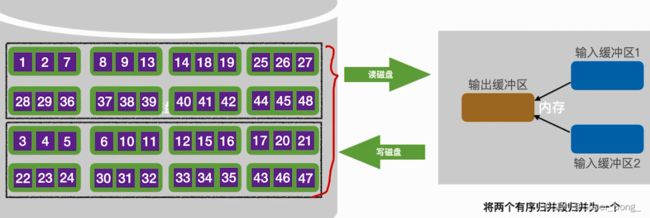
外部排序原理 - 排序过程看视频动画
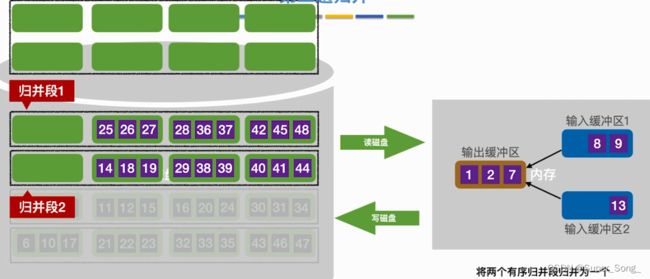
- 原理来自于归并排序
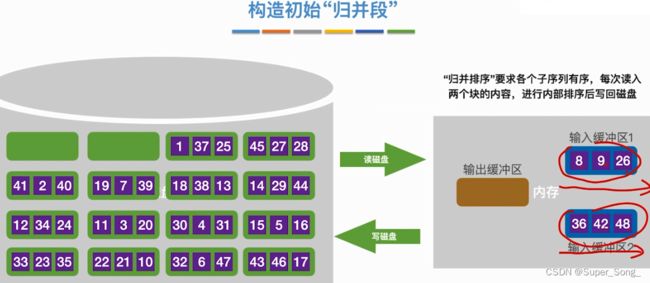
- 内存中需要至少三个缓冲区,一个用来保存归并后的序列,另外两个用来保存归并前的两个子序列
- 两个子序列可以先内部排序一下,再进行归并
- 归并缓冲区如果满了,就写入外存;存子序列的缓冲区如果空了,也立即从外存读磁盘块
- 这和杨一趟下来,外存中得到的就是两两一组的有序序列
- 至此完成了构造初始归并段
- 两两一组进行二路归并


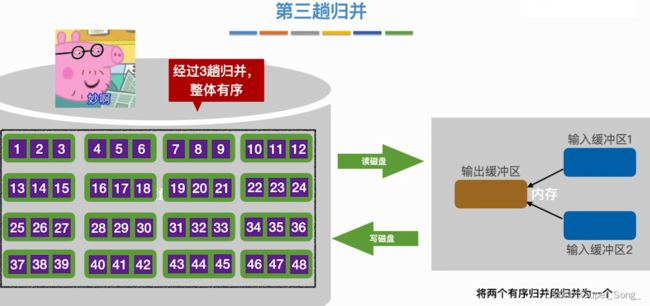
第二趟归并 - 需要注意的是,归并后的序列其实放在另一个磁盘区域中的,原有的会被系统回收
- 这里是为了美观放在了原处
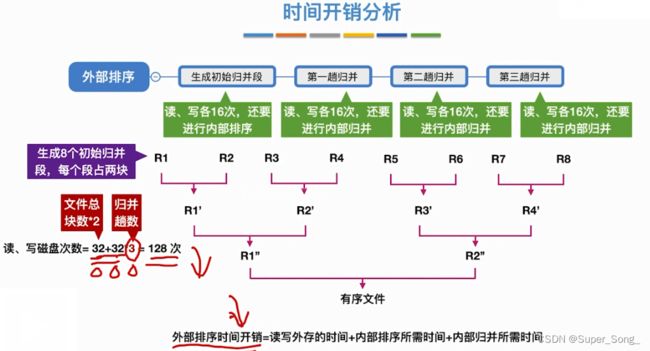
时间开销分析 - 时间开销主要在于磁盘读写
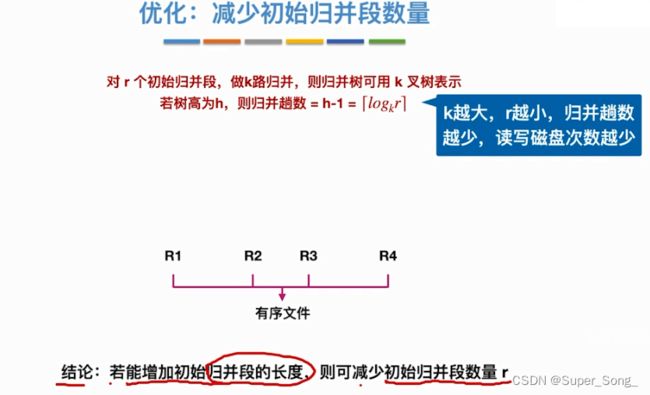
- 若想减少磁盘读写次数,文件总块数不会改变,可以减少归并趟数
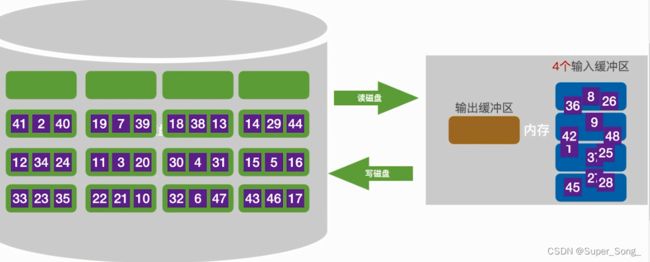
算法优化–多路归并

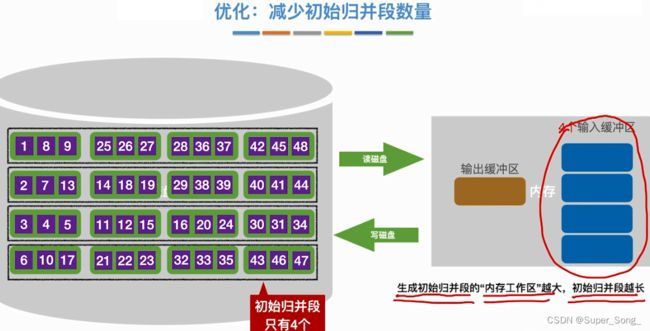
算法优化–减少初始归并段数量
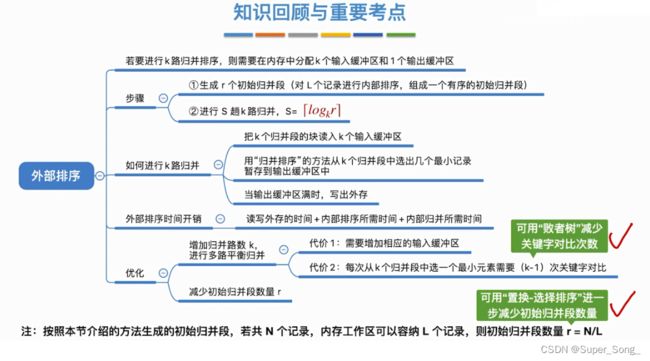
知识点小结
纠正
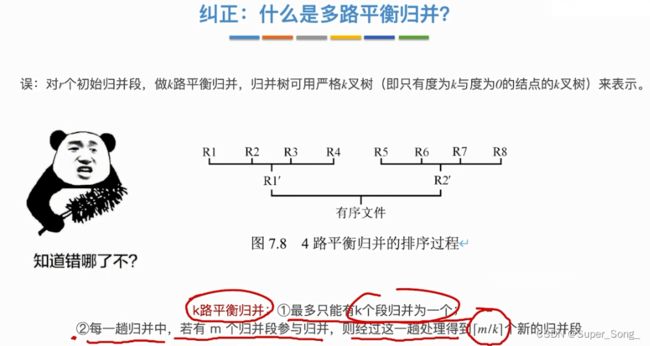

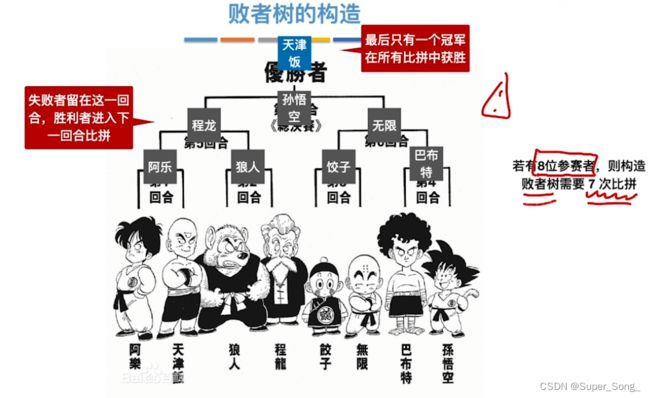
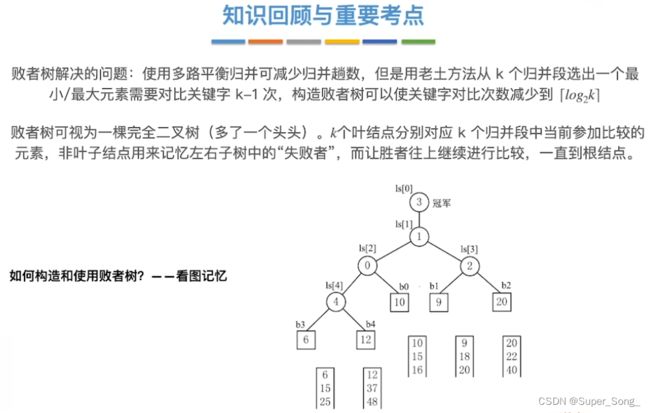
败者树
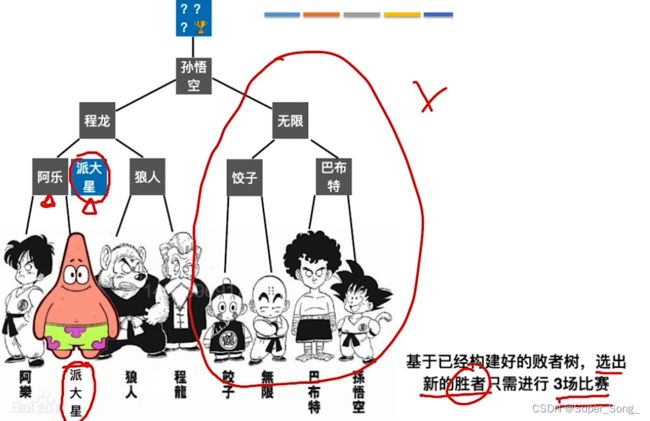
- 是否需要所有人均重新比赛一次?
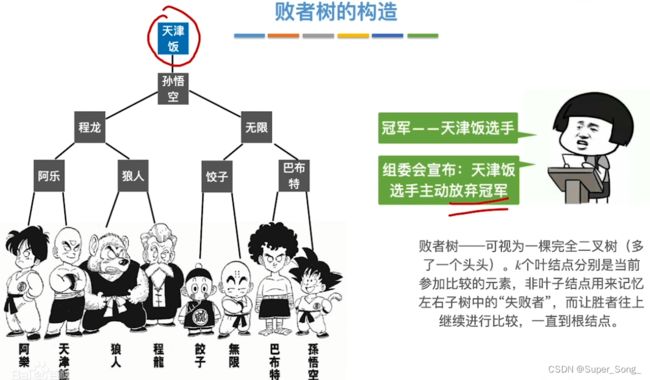
- 其他人无需比赛,派大星只需要沿着天津饭的败者树向上打即可,
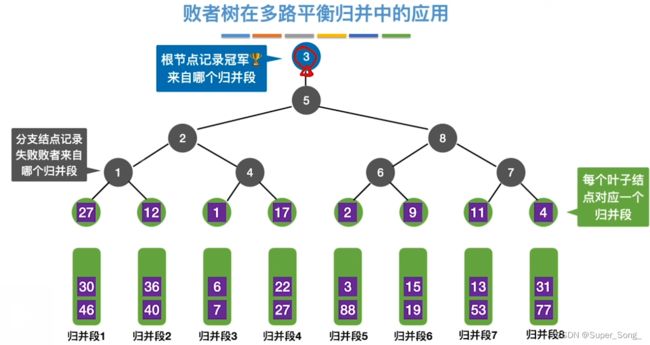
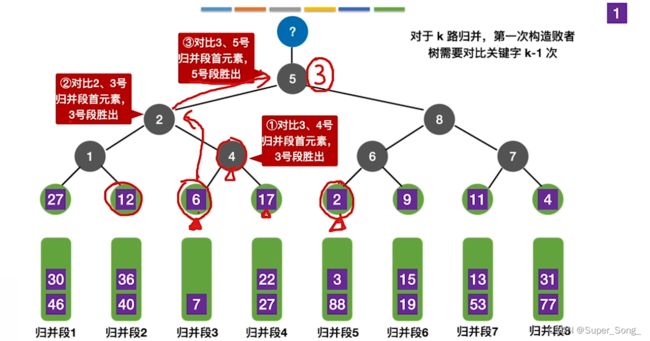
- 第一轮比较时先构建败者树,分支节点记录失败者来自哪个归并段
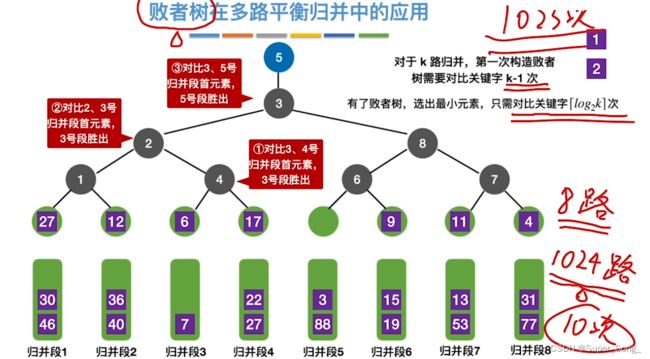
- 当归并3路的1元素离队,新来的元素需要沿着败者树,向上比较,直至重新选出新的最小值
- 归并3路补上6元素
- 考试出现概率不高,即使出现,也是手算
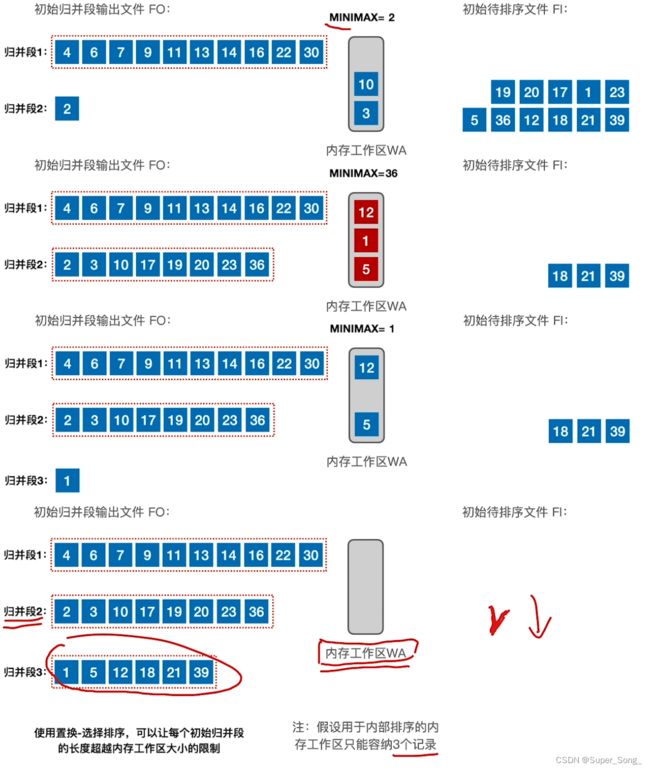
置换–选择排序
外部排序
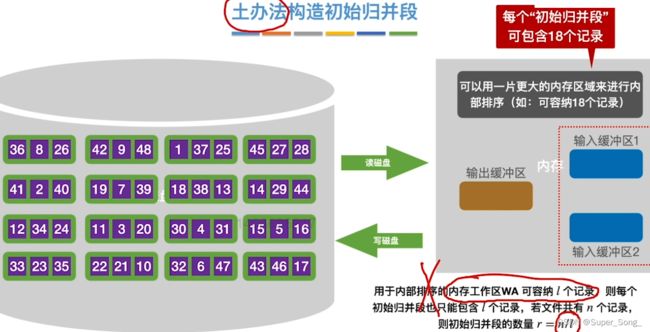
- 减少初始归并段数量,可以降低磁盘的读取次数
- 之前的土办法,一次读取的记录数量,受到内存工作区的限制
- 想减少初始归并段,只能增加内存工作区的大小
- 注意:
- 这里的初始待排文件其实是已经从磁盘读取到缓冲区了,然后再进入到工作区,而不是一个一个元素的从磁盘读
- 从内存工作区输出也是,先写到输出缓冲区,在整体写入到外存中,而不是一个一个元素的写到磁盘
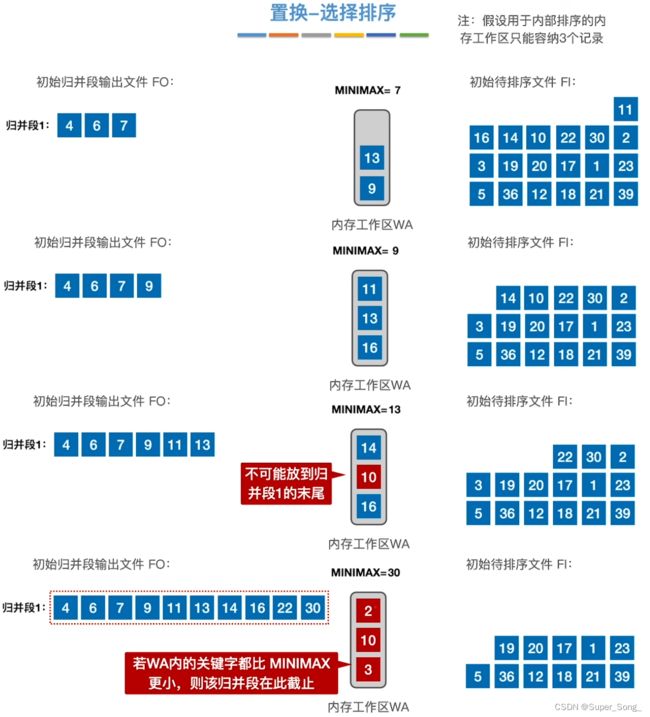
- 从内存工作区不断的选出最小元素,写到输出文件,有空位立刻从待排文件中补上;
- 输出文件中只能从小到大排列,如果遇到更小的,无法再写入,留在工作区,
- 直到工作区满了,无法再写到这个输出文件,这就是一个归并段完成,另起一个归并段,输出
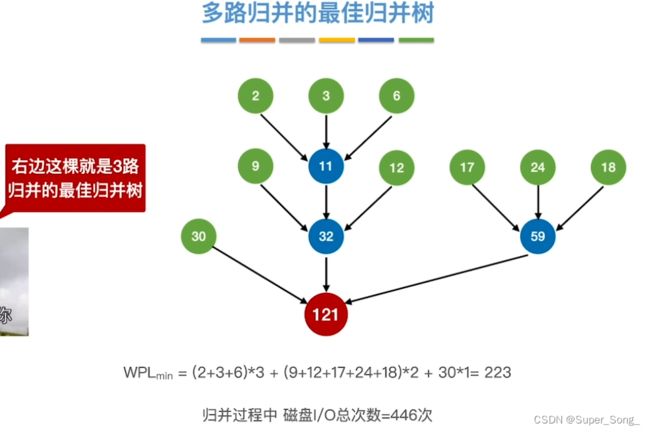
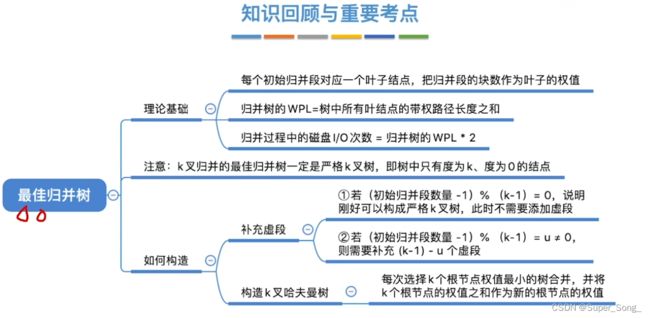
最佳归并树
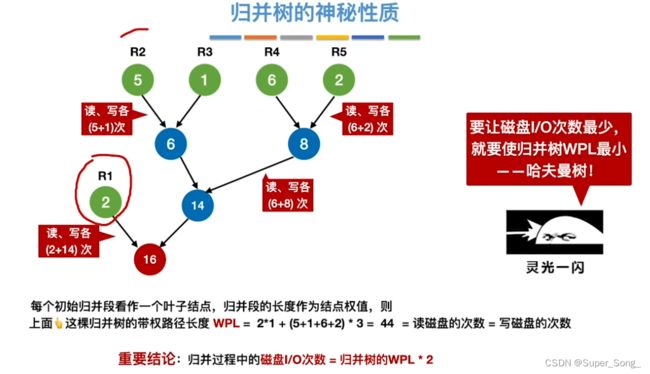
归并树的性质
- 由置换排序构建的初始归并段可能长度各不相同,有些包含较多磁盘块,有些较少
- 每进行一次归并,读写总次数=涉及的所有磁盘快的数量*2
- 这里以二路归并为例,得出二路归并树
- 总结得出,这棵树的带权路径长度*2刚好就是归并树的总的读写次数
- 要想归并树的读写总数最小,就是让树的带权路径最小,即求出哈弗曼树
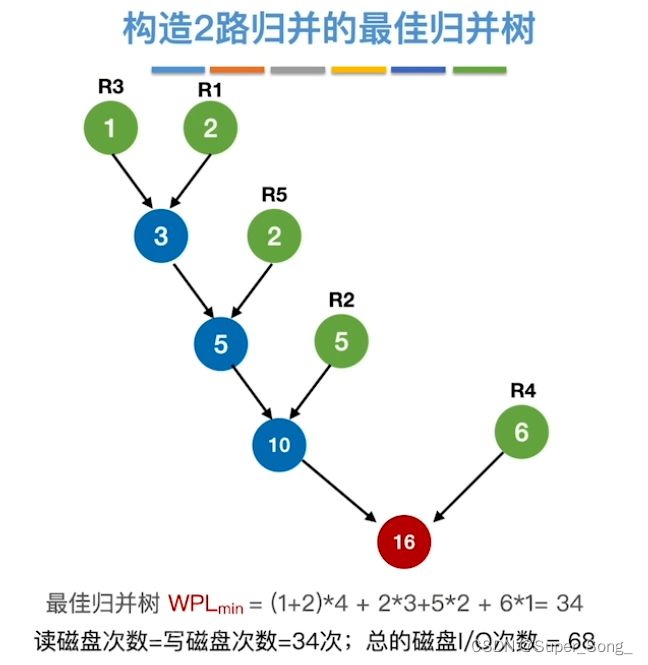
- 让权值最小的两个结点成兄弟
- 新的根结点的权值就是子节点的权值之和
- 再在这些节点(含新节点)中找出权值最小的两个成兄弟
- 以此类推,直至合并至根结点,求出带权路径长度34;总IO次数68比前面的88次减小很多
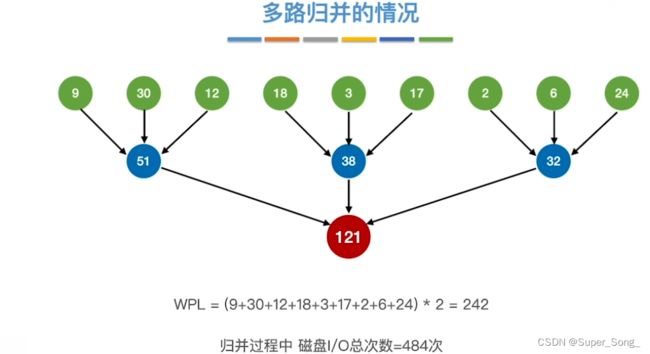
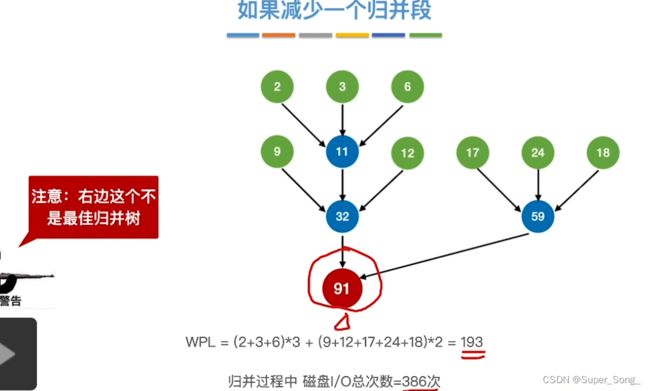
- 导致一个节点少了一路
- 这样构造的归并树不是最佳归并树
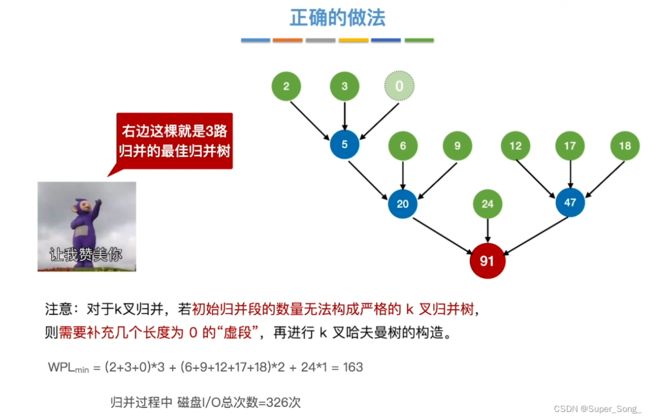
- 正确做法,补上若干个权值为0的节点(虚段),保证归并树的度只能是0和3
- 长度为0的虚段其实就是什么都没有,只是用来占位,辅助我们建立哈弗曼树