深度学习入门之感知机
深度学习入门之感知机
参考书籍:深度学习入门——基于python的理论与实现
文章目录
- 深度学习入门之感知机
- 前言
- 一、感知机是什么?
- 二、简单逻辑电路
-
- 1.与门
- 2.与非门
- 3.或门
- 小结
- 三、感知机的实现
-
- 1.简单实现与门
- 2.导入权重和偏置
- 总结
前言
本文将简单介绍感知机(perceptron)这一算法,感知机是由美国学者Frank Rosenblatt在1957年提出的,为什么要介绍感知机算法呢?主要是因为感知机是作为神经网络(深度学习)的起源的算法。
一、感知机是什么?
感知机接收多个输入信号,输出一个输出信号,但是感知机的信号只有0和1,0表示不传递信号,1表示传递信号。从另外一个角度来讲,感知机也称为‘人工神经元’或者‘朴素感知机’。
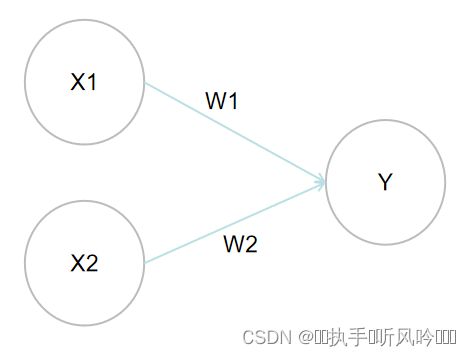
由上图可知,一个接收两个输入信号的感知机,输入信号X1和X2,Y为输出信号,W1和W2是各个输入信号到输出信号的权重。图中的圆圈o称为‘神经元’或者‘节点’。输入信号送进神经元,经过和各自的权重相乘(X1W1、X2W2),得到的结果会被送入输出信号进行求和,只有当这个总和超过了某一个限定值,输出信号才会输出1,这个也称作神经元激活,这个设定值我们称为阈值,用 Q表示。
如果用数学公式表示,感知机的运作过程如下:
当 (X1W1+X2W2≤Q)时,Y输出0;
当(X1W1+X2W2>Q)时,Y输出1.
感知机的多个输入信号都有各自固有的权重参数,这些权重参数控制着各个输入信号的重要性,权重越大,输入信号的重要程度就越高。
二、简单逻辑电路
1.与门
从感知机原理上来说,与门相当于一个两输入一输出的门电路,真值表如下:
| x1 | x2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
如果考虑使用感知机来表示这样一个与门电路的逻辑,只要我们将感知机的权重参数W和输出阈值Q进行一定的设定就可以完成与门逻辑。(W1,W2,Q)满足上述真值表的情况的设定,可能取(W1,W2,Q)=(0.5,0.5,0.7),使用计算公式可以发现:
| x1 | w1 | x2 | w2 | Q | 符号 | y |
|---|---|---|---|---|---|---|
| 0 | 0.5 | 0 | 0.5 | 0.7 | 0x0.5+0x0.5<0.7 | 0 |
| 1 | 0.5 | 0 | 0.5 | 0.7 | 1x0.5+0x0.5<0.7 | 0 |
| 0 | 0.5 | 1 | 0.5 | 0.7 | 0x0.5+1x0.5<0.7 | 0 |
| 1 | 0.5 | 1 | 0.5 | 0.7 | 1x0.5+1x0.5>0.7 | 1 |
通过计算可以很好的发现,感知机实现了与门逻辑。此外,满足这样计算的权重参数不唯一,还有(W1,W2,Q)=(0.5,0.5,0.8)以及(1.0,1.0,1.0)都满足与门逻辑的真值表。
2.与非门
从感知机原理上来说,与非门相当于一个两输入一输出的门电路,其就是相当于将与门的逻辑输出进行一个取反操作,真值表如下:
| x1 | x2 | y |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
如果考虑使用感知机来表示这样一个与非门电路的逻辑,只要我们将感知机的权重参数W和输出阈值Q进行一定的设定就可以完成与非门逻辑。由于只是将输出取反,因此(W1,W2,Q)满足上述真值表的情况的设定,可能取(W1,W2,Q)=(-0.5,-0.5,-0.7),使用计算公式可以发现:
| x1 | w1 | x2 | w2 | Q | 符号 | y |
|---|---|---|---|---|---|---|
| 0 | -0.5 | 0 | -0.5 | 0.7 | 0x-0.5+0x-0.5>-0.7 | 1 |
| 1 | - 0.5 | 0 | -0.5 | 0.7 | 1x-0.5+0x-0.5>-0.7 | 1 |
| 0 | - 0.5 | 1 | -0.5 | 0.7 | 0x-0.5+1x-0.5>-0.7 | 1 |
| 1 | - 0.5 | 1 | -0.5 | 0.7 | 1x-0.5+1x-0.5<-0.7 | 0 |
通过计算可以很好的发现,感知机实现了与非门逻辑。此外,满足这样计算的权重参数也是不唯一,还有(W1,W2,Q)满足与非门逻辑的真值表。
3.或门
从感知机原理上来说,或门相当于一个两输入一输出的门电路,真值表如下:
| x1 | x2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
如果考虑使用感知机来表示这样一个或门电路的逻辑,只要我们将感知机的权重参数W和输出阈值Q进行一定的设定就可以完成或门逻辑。(W1,W2,Q)满足上述真值表的情况的设定,可能取(W1,W2,Q)=(0.5,0.5,0.4),使用计算公式可以发现:
| x1 | w1 | x2 | w2 | Q | 符号 | y |
|---|---|---|---|---|---|---|
| 0 | 0.5 | 0 | 0.5 | 0.4 | 0x0.5+0x0.5<0.4 | 0 |
| 1 | 0.5 | 0 | 0.5 | 0.4 | 1x0.5+0x0.5>0.4 | 1 |
| 0 | 0.5 | 1 | 0.5 | 0.4 | 0x0.5+1x0.5>0.4 | 1 |
| 1 | 0.5 | 1 | 0.5 | 0.4 | 1x0.5+1x0.5>0.4 | 1 |
通过计算可以很好的发现,感知机实现了或门逻辑。此外,满足这样计算的权重参数也是不唯一,还有很多(W1,W2,Q)满足或门逻辑的真值表。
小结
以上过程,利用简单的感知机原理实现了对与、与非、或逻辑,只是权重参数W和阈值Q的变化就使得感知机可以实现不同的逻辑运算。
但是有人可能会发现以上运算,我们都是预先知道了结果,可以说是我们通过结果拼凑出的感知机参数,但是实际上在计算机上,它们并不会如此选择参数。所以学习合适的参数的过程,就是机器学习的学习过程,将训练数据交给计算机,计算机自动决定参数值。
三、感知机的实现
1.简单实现与门
代码如下(示例):
def and(x1,x2):
w1,w2,theta = 0.5,0.5,0.7
temp=x1*w1+x2*w2
if temp <= theta:
return 0
elif temp > theta:
return 1
else
print('error!')
在函数内初始化权重参数w1,w2,阈值参数theta,,当输入信号的加权总和超过阈值就返回1,否则为0.
| 输入函数 | 输出结果 |
|---|---|
| and(0,0) | 0 |
| and(0,1) | 0 |
| and(1,0) | 0 |
| and(1,1) | 1 |
通过上述结果,发现输出结果和与门逻辑的真值表一致,就简单实现了与逻辑。按照相同的步骤,我们也可以实现与非门、或门逻辑,只是对应的权重参数以及阈值参数不同而已。
2.导入权重和偏置
上述简单的与门实现,比较直接简单,但是考虑到后续方便,我们将其形式改为另一种形式,即将偏置参数Q换为-b,感知机的行为如下:
当 (X1W1+X2W2+b≤0)时,Y输出0;
当(X1W1+X2W2+b>0时,Y输出1.
只是换了一种形式而已,结果完成一致,b称为偏置,W1和W2称为权重,整个运算过程:感知机计算输入信号的加权和,并再和偏置相加得到最后的结果,结果大于0则输出1,否则输出为0。这种结构,我们可以更好使用Numpy来实现。
代码如下(示例):
import numpy as np
def and(x1,x2):
x=np.array([x1,x2])
w=np.array([0.5,0.5])
b=0.7
temp=np.sum(w*x)+b
if temp <= 0:
return 0
else
return 1
权重参数W和偏置参数b控制作用不同,权重参数控制输入信号的重要性程度,偏置参数控制整个神经元被激活的容易程度,如b=-0.1,则只需要输入信号的加权和超过0.1,神经元就会被激活,但是如果b=-20,那么输入函数的加权和就必须达到20,神经元才会被激活。
因此,只要改变权重参数和偏置参数,就可以很简单的实现其他逻辑,例如与非门:
import numpy as np
def Nand(x1,x2):
x=np.array([x1,x2])
w=np.array([-0.5,-0.5])
b=-0.7
temp=np.sum(w*x)+b
if temp <= 0:
return 0
else
return 1
总结
简单对感知机进行介绍,也通过感知机原理实现了与逻辑、与非逻辑、或逻辑,但是现在描述的感知机还是处于较为简单的,属于单层感知机,功能还是比较单一,单层感知机只能够通过一根直线划分空间,只能进行线性空间划分,但是实际上,我们遇到的问题大都为非线性空间,即需要使用曲线进行划分,这个对单层感知机来说,还无法实现,这也是单层感知机的一个局限性。