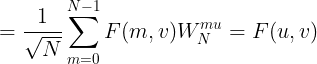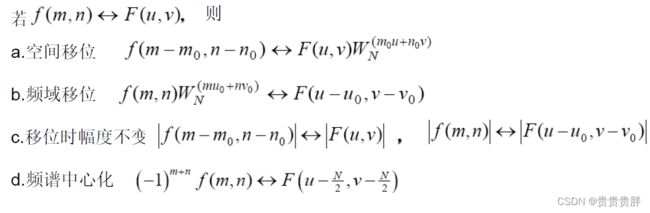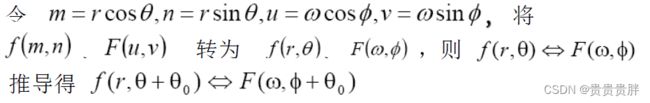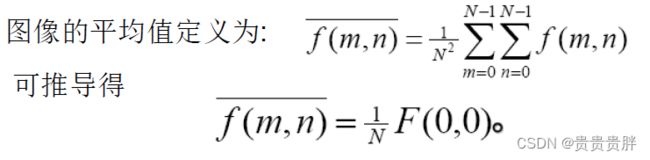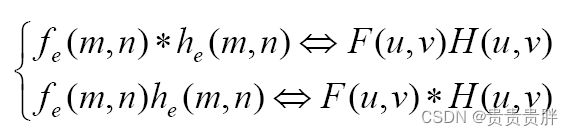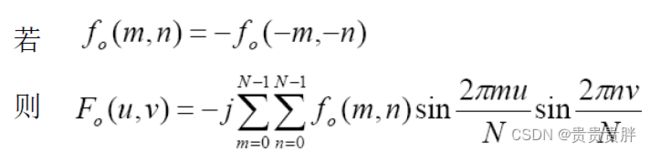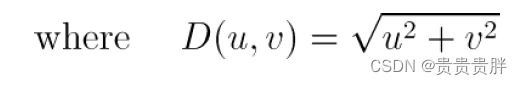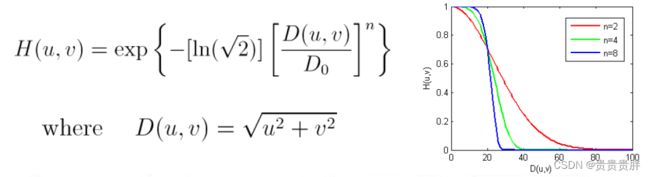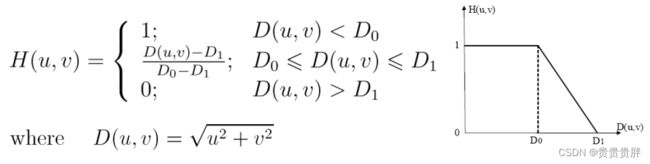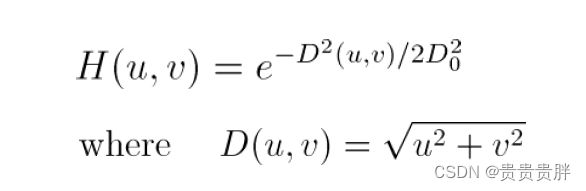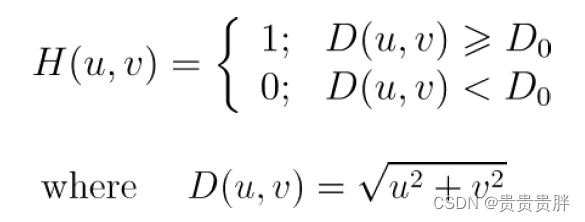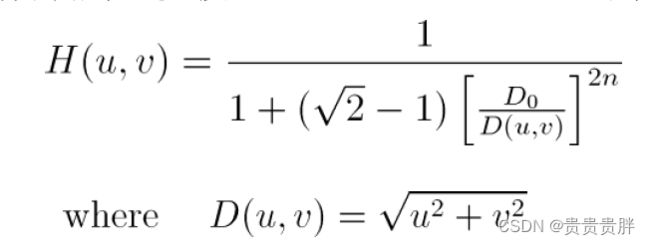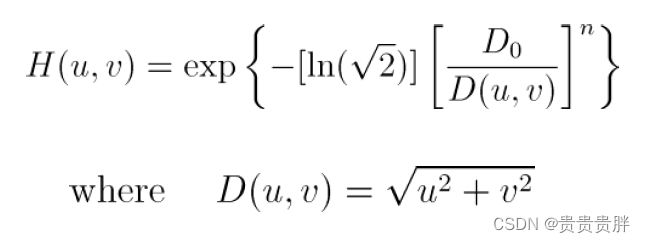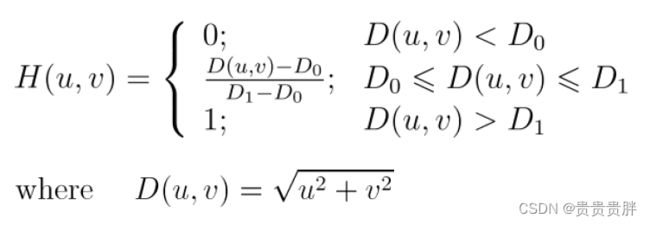第四章 图像频域滤波
本章主要内容为二维傅立叶变换及其反变换,频域平滑滤波器、频域锐化滤波器,以及同态滤波器的相关介绍。
本章要求重点掌握图像频域滤波的基本流程及表示;二维离散傅里叶变换的表示及特点;频域平滑滤波器的基本原理和目的,三种典型滤波器;频域锐化滤波器的基本原理和目的,三种典型滤波器;同态滤波器的基本原理和目的。
本章科普内容为图像变换域滤波;离散傅里叶变换;频域带通滤波器。
4.1 二维傅里叶变换及其反变换
4.1.1 图像变换域滤波
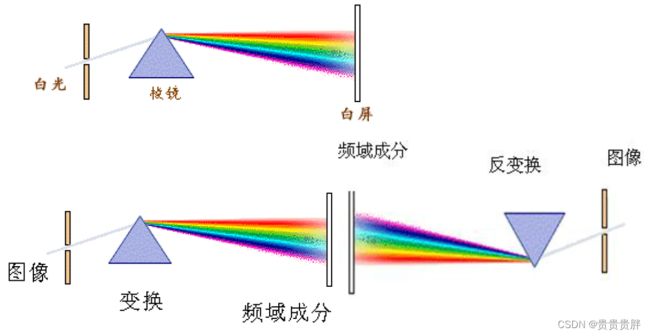
图像虽然具有明确视觉意义,但人眼并不能从中直接看出频域信息。通过变换,找出图像的频率成分,有助于图像的增强、去噪。
4.1.2 图像频域滤波
频率滤波需要先进行傅里叶变换,将图像的空域信息转换到频域进行处理,然后再反变换回空域还原为图像,具体流程如下:
参考二维傅里叶变换及逆变换公式:
上述模型中用到的FFT和IFFT对应于快速傅里叶变换与快速傅里叶反变换,空域滤波对应的频域滤波可依次由以下三个公式简单表示:
4.1.3 正弦型变换:离散傅里叶变换(DFT)
4.1.3.1 一维离散傅里叶变换(1D-DFT)
对于有限长序列f(n) (n = 0, 1, 2, ·····, N-1),其DFT为:
1D-DFT矩阵表示:
其中U称为变换矩阵,从U的构成形式可知:
![]()
![]()
由此可知,U是一个酉矩阵,且
![]()
所以1D-DFT是正交变换,其反变换为:
![]()
4.1.3.2 二维离散傅里叶变换(2D-DFT)
令f(x, y)表示一幅大小为M×N像素的数字图像,其中x=0, 1, 2, ···, M-1,y=0, 1, 2, ···, N-1。由F(u,v)表示的f(x, y)的二维离散傅里叶变换(DFT)及二维离散傅里叶反变换由下式给出:
其中,m, n, u, v均为整数,0 ≤ m, n, u, v ≤ N-1。使用确定频率的变量u和v,可以将指数项展开为正弦函数和余弦函数。频率域是使用u和v作为(频率)变量,由F(u, v)构成的坐标系,而空间域是使用x和y作为(空间)变量,由f(x, y)构成的坐标系。
傅里叶变换表示为复数形式:
![]()
傅里叶变换表示成为指数形式:
![]()
幅度谱: ![]()
功率谱: ![]()
4.1.3.3 2D-DFT的性质
(1)变换核的可分离性
在离散傅里叶变换中,变换核为:
![]()
![]()
变换核的可分离性说明2D-DFT可通过两次1D-DFT完成,具体计算如下:
因此,我们无论从行方向还是列方向开始对 ![]() 进行1D-DFT,都可以得到最终的二维傅里叶变换:
进行1D-DFT,都可以得到最终的二维傅里叶变换:
(2)移位特性
(3)周期性和共轭特性
(4)旋转不变性
(5)比例尺(尺度变换)
(6)平均性
(7)卷积定理
(8)实偶函数的DFT
![]()
(9)实奇函数的DFT
4.2 图像频域滤波
4.2.1 频域低通滤波器
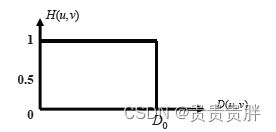
(1)理想低通滤波器(ILPF)
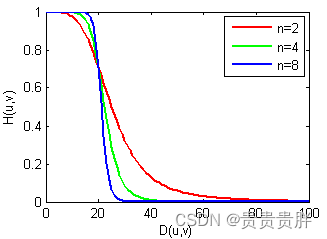
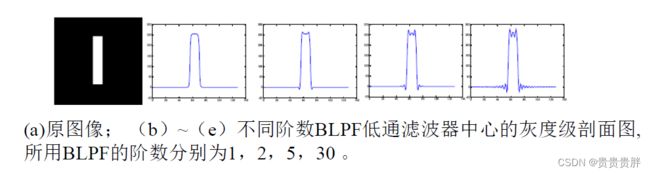
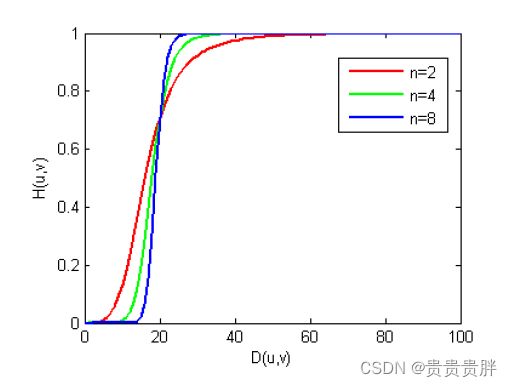
(2)Butterworth低通滤波器(BLPF)
n为整数,称为滤波器的阶数,n越大,通带和阻带的近似性越好,过渡带也越陡。
(3)指数低通滤波器(ELPF)
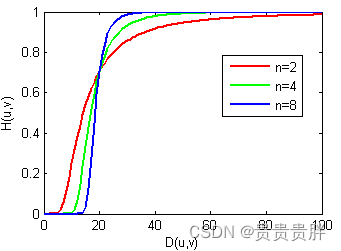
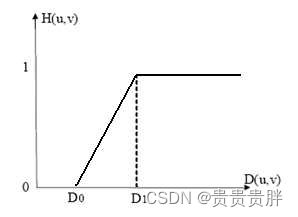
(4)梯形低通滤波器(TLPF)
(5)高斯低通滤波器(GLPF)
高斯滤波器的空域和频域形式相同,从频域来看没有振铃现象。
4.2.2 频域高通滤波器
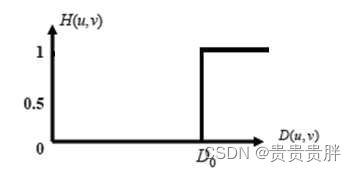
(1)理想高通滤波器(IHPF)
(2)Butterworth高通滤波器(BHPF)
(3)指数高通滤波器(EHPF)
(4)梯形高通滤波器(THPF)
4.2.3 频域带通滤波器
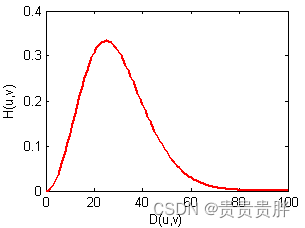
(1)双高斯差带通滤波器(DOG)
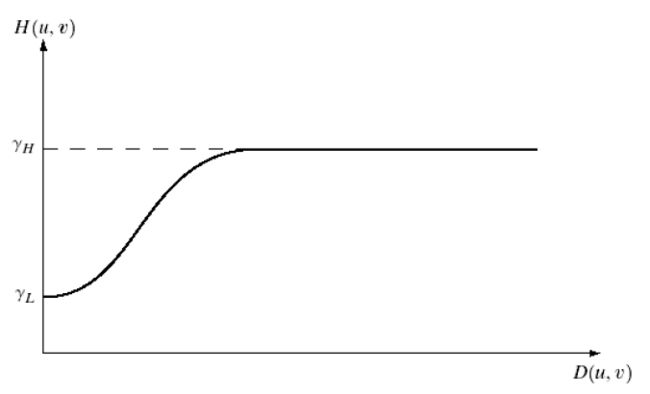
4.3 同态滤波
同态滤波是一种把频率过滤和灰度变换结合起来的图像处理方法。它根据图像的照度反射模型,利用压缩亮度范围和增强对比度来改善图像质量。
同态滤波主要为了解决:(1)光照不均匀,则使图像上对应于照度暗的区域,无法分辨细节;(2)动态范围过大,如在夏日强光照射下成像,景物细节无法区分。
同态滤波可以增强图像暗区细节,同时又不损失图像亮区细节。
![]()
入射分量 ![]() 在空间缓慢变化,处于低频区域;
在空间缓慢变化,处于低频区域;
反射分量![]() 反映细节,处于高频区域。
反映细节,处于高频区域。
同态滤波的滤波滤波步骤:
(1)图像光照模型建模:
![]()
(2)变换到对数坐标系(注意条件!!!)
![]()
(3)变换到频域
![]()
![]()
(4)用传递函数H实施频域滤波
![]()
(5)变换回时域
![]()
(6)变换回原坐标
![]()

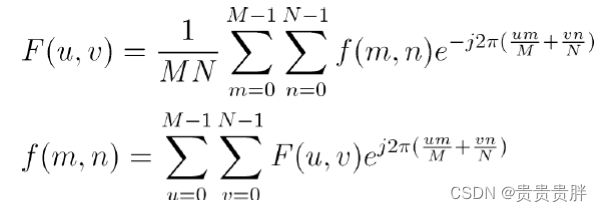

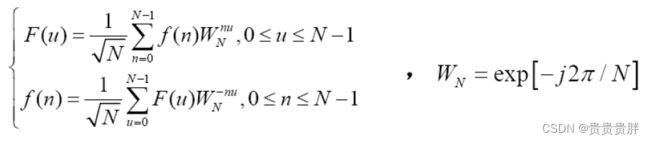
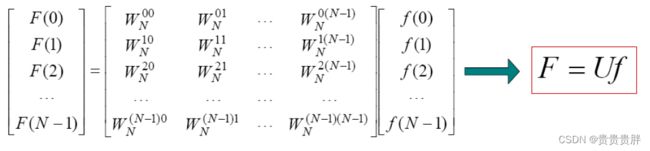
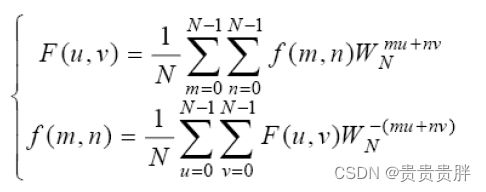
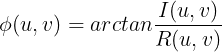
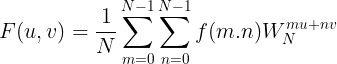
![\large =\frac{1}{\sqrt{N}}\sum_{m=0}^{N-1}[\frac{1}{\sqrt{N}}\sum_{n=0}^{N-1}f(m,n)W_{N}^{nv}]W_{N}^{mu}](http://img.e-com-net.com/image/info8/091a45563cb840129974d54c4dad909a.gif)