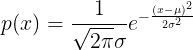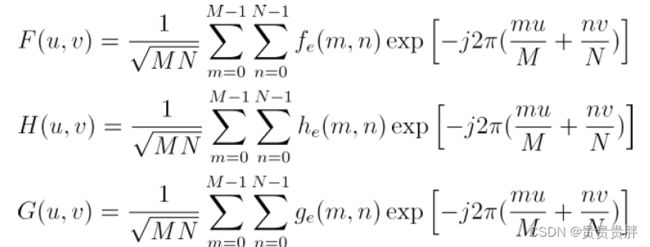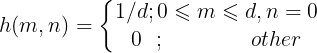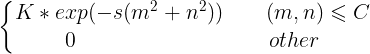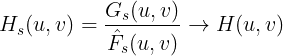第五章 图像复原

        本章主要内容为图像退化模型与噪声模型、图像的空域复原和频域复原方法、退化函数的估计方法、逆滤波、维纳滤波、约束最小二乘滤波。

        本章要求重点掌握的内容为四种典型的图像噪声的表现特点；图像退化的数学模型；三种典型的退化函数；退化函数的估计方法。

        本章科普内容为图像退化过程的产生原因；图像退化函数的辨识；Wiener滤波。

5.1 图像噪声

5.1.1 白噪声（White Noise）

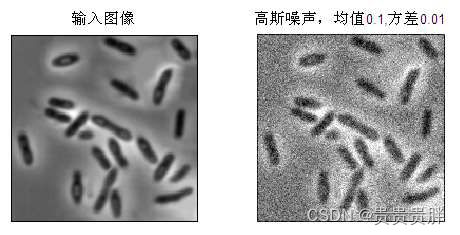
        白噪声具有常量的功率谱，其一个特例是高斯噪声（Gaussian Noise），其直方图曲线服从一维高斯模型分布：

         为均值与标准差。MATLAB函数为 J=imnoise(I, 'gaussian', M, V)，M,V为均值和标准差。

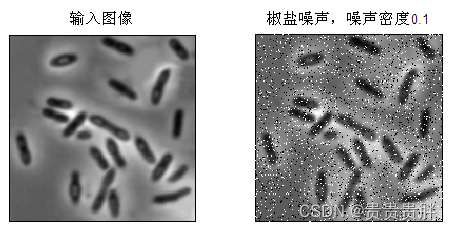
 5.1.2 椒盐噪声（Pepper & Salt Noise）

        椒盐噪声是一种在图像中产生黑色、白色点的脉冲噪声。该噪声在图像中显现较为明显，对图像分割、边缘检测、特征提取等后续处理具有严重破坏作用。

        MATLAB函数为J=IMNOISE(I, 'salt & pepper', D)，D为噪声密度。

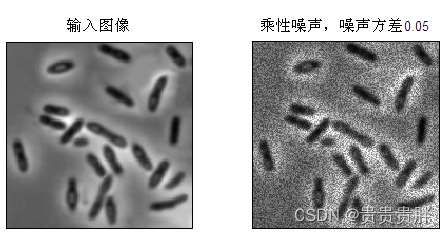
 5.1.3 乘性噪声（Multiplication Noise）

        乘性噪声与加性噪声对应，加性噪声一般指热噪声、散弹噪声等，它们与原始信号的关系是相加，不管有没有原始信号，噪声都存在。而乘性噪声一般由信道不理想引起，它们与信号的关系是相乘，依附于信号而存在。

        MATLAB产生函数为J=imnoise(I, 'speckle', V)，V为噪声方差。

 5.1.4 量化噪声（Quatization Noise）

        在量化级别不同时出现的噪声。例如，将图像的亮度级别减少到1/16时会出现伪轮廓。量化噪声可以从直方图分布予以分析。

5.2 图像退化 

5.2.1 图像退化形式、图像复原目的

        图像复原是早期图像处理的主要内容之一，目的在于消除或减轻在图像获取及传输过程中造成的图像品质下降即退化现象，恢复图像的本来面目。

        退化包括由成像系统光学特性造成的歧变，以及噪声和相对运动造成的模糊等情况。

        图像复原是试图利用退化过程的先验知识，去恢复已被退化图像的本来面目。

        图像复原的基本思路是先建立退化的数学模型，然后根据该模型对退化图像进行拟合。图像复原可以在空域进行处理，也可以在频域进行处理。

5.2.2 图像退化产生原因

        图像退化产生过程包括：光学系统的像差、大气流的扰动效应、摄影胶片的非线性、图像运动造成的模糊、光学系统中的几何畸变、传感器非线性。

 5.2.3 图像退化的数学模型

        设一成像系统的物像映射关系（或说退化图像）为：

        模型表示为：

        可以理解为成像系统作用的运算符，实际成像系统在一定条件下可近似看作线性移不变系统，图像恢复过程中往往使用线性移不系统模型。

        复杂激励f(x, y) 等于无数个函数激励之和。   

        函数选择性：

        系统脉冲响应（点扩散函数，PSF: Point-Spread Function）:

        先求出系统对基元函数的响应（输出）表达式（即系统脉冲响应），再乘以相应权重因子后求和，就可以得到退化图像。

        根据移不变性质：

        近代光学中用成像概念来描述的退化图像（degraded image）的数学表达式。

        图像退化过程一般看作是噪声的污染过程，且假定噪声是加性白噪声，这时退化后的图像为：

        模型表示为：

         H[]可理解为综合所有退化因素的函数，实际成像系统在一定条件下可近似看作是线性以不变系统，图像恢复过程中往往使用线性移不变的系统模型，利用矩阵模型表示为：

        g, f, n为图像排成的列向量。

        图像频域的退化公式：

        模型表示为： 

        利用FFT，可以将g, f, n转化到频域：

 5.2.4 常见退化函数

 5.2.4.1 线性运动退化函数

        由于目标与成像系统间的相对匀速直线运动形成的退化。水平方向的线性运动可表示为：

 5.2.4.2 焦散退化函数

        几何光学分析表明，光学系统焦散造成的图像退化对应的点扩散函数应该是一个均匀分布的圆形光斑，可表示为：

 5.2.4.3 高斯退化函数

         高斯退化函数是许多光学测量系统和成像系统最常见的退化函数。在这些系统中，由于决定系统点扩散函数的因素较多，其综合效果往往使最终的点扩散函数趋近于高斯型。

        其中K是归一化常数，是一个正常数，C是圆形支持域。下图为高斯退化图像。

5.3 图像退化函数的辨识

5.3.1图像观察法

        对于一幅模糊图像，首先提取包含简单结构的一小部分图像，然后根据这部分图像中目标和背景的灰度级，就可以构建一幅不模糊的图像，该图像与观察到的子图像具有相同的大小和特性。

        

5.3.2 试验估计法

        使用与获取退化图像的设备相似的设备，那么利用相同的系统设置，就可以由成像一个脉冲（小亮点）得到退化函数的冲击响应。亮点必须尽可能的亮，达到减少噪声干扰的目的。由于冲激响应的DFT为常量，有：

5.3.3 数学建模法

        利用引起退化的物理环境来建立退化模型，如Hufnagel和Stanley提出的基于大气湍流图例推行的退化模型：

5.4 图像恢复

5.4.1 无约束恢复和有约束恢复

5.4.1.1 无约束恢复

        从前面建立的模型可知，无约束是令||n||²最小：

5.4.1.2 有约束恢复

·        令Q是f的线性算子，有约束是令||Qf||²最小：

5.4.2 维纳滤波

        令  是原始图像和噪声的相关矩阵，其中：

令

        则原始图像在最小均方误差准则下的最佳恢复解为：

         维纳滤波的频域表示：