数值分析实验三 线性方程组数值解法
一、目的与要求：
1、熟悉求解线性方程组的有关理论和方法；
2、会编制列主元消去法、LU 分解法、雅可比及高斯—塞德尔迭代法德程序；
3、通过实际计算，进一步了解各种方法的优缺点，选择合适的数值方法。
二、实验内容
1、列主元高斯消去法
- 算法
将方程用增广矩阵
表示
1.消元过程
对k=1,2,…,n-1
①选主元，找使得
②如果
，则矩阵A奇异，程序结束；否则执行③。
③如果
，则交换第k行与第
行对应元素位置，
j=k,┅,n+1
④消元，对i=k+1, ┅,n计算
对j=l+1, ┅,n+1计算
2.回代过程
- 程序与实例
- 程序代码
#include
double A[10][10];
double B[10];
double X[10];
int n;
void swap_row(int a, int b)
{
double t;
int i;
for (i = 1; i <= n; i++)
{
t = A[a][i];
A[a][i] = A[b][i];
A[b][i] = t;
}
t = B[a];
B[a] = B[b];
B[b] = t;
}
int find_rowmax(int k, int n){
int rowmax = k;
double max = 0;
int i;
for (i = k; i <= n; i++)
{
if (max < fabs(A[i][k]))
{
max = fabs(A[i][k]);
rowmax = i;
}
}
if (rowmax != k)
swap_row(rowmax, k);
if (max == 0)
{
return 1;
}
else return 0;
}
void print_matrix(int k)
{
int i;
int j;
printf("\n step %d\n",k);
printf("Augmented matrix: \n");
for (i = 1; i <= n; i++)
{
for (j = 1; j <= n; j++)
{
printf("%f", A[i][j]);
printf(" ");
}
printf("%lf", B[i]);
printf("\n");
}
}
int main()
{
int i,j,k,l,m;
double t;
clrscr();
printf("Please enter the order of the coefficient matrix:");
scanf("%d", &n);
printf("Please enter augmented matrix: \n");
for (i = 1; i <= n; i++)
{
for (j = 1; j <= n; j++)
{
scanf("%lf", &t);
A[i][j] = t;
}
scanf("%lf", &t);
B[i] = t;
}
for (k = 1; k < n; k++)
{
int flag = find_rowmax(k, n);
if (flag == 1)
{
return 0;
};
for (l = k + 1; l <= n; l++)
{
double q = A[l][k] / A[k][k];
for (m = k; m <= n; m++)
{
A[l][m] -= q * A[k][m];
}
B[l] -= q * B[k];
}
print_matrix(k);
}
for (i = n; i >= 1; i--)
{
for (j = n; j > i; j--)
{
B[i] -= A[i][j] * X[j];
}
X[i] = B[i] / A[i][i];
}
printf("result:");
for (i = 1; i <= n; i++)
{
printf("\nx[%d] = %lf", i,X[i]);
printf(" ");
}
getch();
} - 实验结果
2、矩阵直接三角分解法
- 算法
将方程组Ax=b 中的A分解为A=LU，其中L为单位下三角矩阵，U为上三角矩阵，则方程组Ax=b化为解2个方程组Ly=b，Ux=y，具体算法如下：
①对j=1,2,3,…,n计算
对i=2,3,…,n计算 
②对k=1,2,3,…,n:
a. 对j=k,k+1,…,n计算
b. 对i=k+1,k+2,…,n计算
③
，对k=2,3,…,n计算
④
,对k=n-1,n-2,…,2,1计算
注：由于计算u的公式于计算y的公式形式上一样，故可直接对增广矩阵
施行算法②，③，此时U的第n+1列元素即为y。
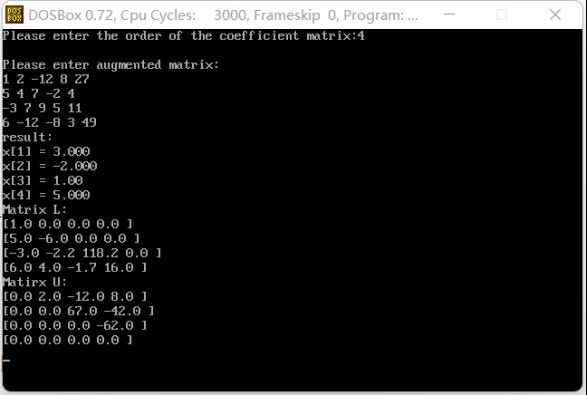
- 程序与实例
- 程序代码
#include
#include
double a[20][20],x[20];
int main()
{
float aaa,*bbb=&aaa;
int n;
int i, j, k,r;
double* x;
clrscr();
printf("Please enter the order of the coefficient matrix:");
scanf("%d", &n);
if (n > 20)
{
return 1;
}
if (n <= 0)
{
return 1;
}
printf("\nPlease enter augmented matrix: \n");
for (i = 0; i < n; i++) {
for (j = 0; j < n+1; j++)
{
scanf("%lf", &a[i][j]);
}
}
x = (float*)malloc(n * sizeof(float));
for (r = 0; r <= n - 1; r++)
{
for (i = r; i <= n; i++)
for (k = 0; k <= r - 1; k++)
a[r][i] -= a[r][k] * a[k][i];
for (i = r + 1; i <= n - 1; i++)
{
for (k = 0; k <= r - 1; k++)
a[i][r] -= a[i][k] * a[k][r];
a[i][r] /= a[r][r];
}
}
for (i = n - 1; i >= 0; i--)
{
for (r = n - 1; r >= i + 1; r--)
a[i][n] -= a[i][r] * x[r];
x[i] = a[i][n] / a[i][i];
}
printf("result:\n");
for (i = 0; i < n; i++) {
printf("x[%d] = %.3f\n", i+1, x[i]);
}
printf("Matrix L:\n");
for (i = 0; i < n; i++)
{
printf("[");
for (j = 0; j <=i ; j++)
{
printf("%.1f ",a[i][j]);
}
for (j = i+1; j < n; j++)
{
printf("0.0 ");
}
printf("]\n");
}
printf("Matirx U:\n");
for (i = 0; i < n; i++)
{
printf("[");
for (j = 0; j <= i; j++)
{
printf("0.0 ");
}
for (j = i+1; j < n; j++)
{
printf("%.1f ", a[i][j]);
}
printf("]\n");
}
getch();
return 0;
} 
3、迭代法
3.1 雅可比迭代法
- 算法
设方程组Ax=b系数矩阵的对角线元素
,M为迭代次数容许的最大值,ε为容许误差。
①取初始向量
，令k=0。
②对i=1,2,…,n 计算
③如果
，则输出
，结束；否则执行④。
④如果k≥M,则不收敛，终止程序；否则
,转②。
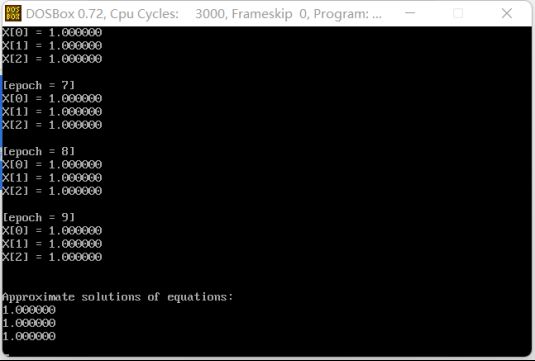
- 程序与实例
- 程序代码
#include
#include
#include
#define MaxSize 20
double A[MaxSize][MaxSize];
double B[MaxSize];
double D[MaxSize][MaxSize];
double E[MaxSize][MaxSize];
double F[MaxSize];
double X[MaxSize];
double X1[MaxSize];
float e;
int n;
int epoch;
void InitMatrix()
{
int i, j;
for (i = 0; i < n; i++)
for (j = 0; j < n; j++)
{
if (i == j)
{
D[i][j] = 1 / A[i][i];
E[i][j] = 0;
}
if (i < j)
E[i][j] = A[i][j];
if (i > j)
E[i][j] = A[i][j];
}
}
void Jacobi()
{
int i, j, k, r;
double sum1, sum2 = 0;
for (i = 0; i < n; i++)
for (j = 0; j < n; j++)
{
sum1 = 0;
for (k = 0; k < n; k++)
{
sum1 = sum1 + D[i][k] * E[k][j];
}
E[i][j] = -sum1;
}
for (i = 0; i < n; i++)
{
sum2 = 0;
for (k = 0; k < n; k++)
{
sum2 = sum2 + D[i][k] * B[k];
}
F[i] = sum2;
}
for (r = 1; r < epoch; r++)
{
int flag = 0;
double sum3;
for (i = 0; i < n; i++)
X1[i] = X[i];
for (i = 0; i < n; i++)
{
sum3 = 0;
for (k = 0; k < n; k++)
{
sum3 = sum3 + E[i][k] * X1[k];
}
X[i] = F[i] + sum3;
}
for (j = 0; j < n; j++)
if (fabs(X[j] - X1[j]) < e)
flag++;
if (flag == n)
{
printf("\nThe %d iteration time satisfies the accuracy!\n", r);
break;
}
printf("\n[epoch = %d] \n", r);
for (i = 0; i < n; i++)
printf("X[%d] = %lf\n", i, X[i]);
}
}
void input()
{
int i, j;
printf("Please enter coefficient matrix A:\n");
for (i = 0; i < n; i++)
for (j = 0; j < n; j++)
scanf("%lf", &A[i][j]);
printf("Please enter vector b:\n");
for (i = 0; i < n; i++)
scanf("%lf", &B[i]);
printf("Please enter the initial vector X:\n");
for (i = 0; i < n; i++)
scanf("%lf", &X[i]);
printf("Please enter the allowable error E:\n");
scanf("%f", &e);
printf("Please enter the number of iterations Epoch:\n");
scanf("%d", &epoch);
}
void print()
{
int i;
printf("\n\nApproximate solutions of equations:\n");
for (i = 0; i < n; i++)
printf("%lf\n", X[i]);
}
int main()
{
clrscr();
printf("Please enter the order of the coefficient matrix: \n");
scanf("%d", &n);
printf("\n");
input();
InitMatrix();
Jacobi();
print();
getch();
return 0;
} 
3.2 高斯-塞尔德迭代法
- 算法
设方程组Ax=b的系数矩阵的对角线元素,
,M为迭代次数容许的最大值,ε为容许误差
①取初始向量
,令k=0。
②对i=1,2,…,n计算
③如果
，则输出
,结束；否则执行④。
④如果
则不收敛，终止程序；否则
,转②。
- 程序与实例
- 程序代码
#include#include #include #define MaxSize 20 double A[MaxSize][MaxSize]; double B[MaxSize]; double D[MaxSize][MaxSize]; double E[MaxSize][MaxSize]; double F[MaxSize]; double X[MaxSize]; double X1[MaxSize]; float e; int n; int epoch; void InitMatrix() { int i, j; for (i = 0; i < n; i++) for (j = 0; j < n; j++) { if (i == j) { D[i][j] = 1 / A[i][i]; E[i][j] = 0; } if (i < j) E[i][j] = A[i][j]; if (i > j) E[i][j] = A[i][j]; } } void GauseSeidel() { int i, j, k, r; double sum1, sum2 = 0; for (i = 0; i < n; i++) for (j = 0; j < n; j++) { sum1 = 0; for (k = 0; k < n; k++) { sum1 = sum1 + D[i][k] * E[k][j]; } E[i][j] = -sum1; } for (i = 0; i < n; i++) { sum2 = 0; for (k = 0; k < n; k++) { sum2 = sum2 + D[i][k] * B[k]; } F[i] = sum2; } for (r = 1; r < epoch; r++) { int flag = 0; double sum3; for (i = 0; i < n; i++) X1[i] = X[i]; for (i = 0; i < n; i++) { sum3 = 0; for (k = 0; k < n; k++) { if (k < i) { sum3 = sum3 + E[i][k] * X[k]; } else{ sum3 = sum3 + E[i][k] * X1[k]; } X[i] = F[i]+sum3; } } for (j = 0; j < n; j++) if (fabs(X[j] - X1[j]) < e) flag++; if (flag == n) { printf("\nThe %d iteration time satisfies the accuracy!\n", r); break; } printf("\n[epoch = %d] \n", r); for (i = 0; i < n; i++) printf("X[%d] = %lf\n", i, X[i]); } } void input() { int i, j; printf("Please enter coefficient matrix A:\n"); for (i = 0; i < n; i++) for (j = 0; j < n; j++) scanf("%lf", &A[i][j]); printf("Please enter vector b:\n"); for (i = 0; i < n; i++) scanf("%lf", &B[i]); printf("Please enter the initial vector X:\n"); for (i = 0; i < n; i++) scanf("%lf", &X[i]); printf("Please enter the allowable error E:\n"); scanf("%f", &e); printf("Please enter the number of iterations Epoch:\n"); scanf("%d", &epoch); } void print() { int i; printf("\n\nApproximate solutions of equations:\n"); for (i = 0; i < n; i++) printf("%lf\n", X[i]); } int main() { clrscr(); printf("Please enter the order of the coefficient matrix: \n"); scanf("%d", &n); printf("\n"); input(); InitMatrix(); GauseSeidel(); print(); getch(); return 0; } 
三、分析思考
本次实验实现了在C语言下用列主元消去法，直接三角分解法和迭代法求解线性方程组。在不计浮点数位数带来的舍入误差的情况下，列主元消去法和直接三角分解法均能够求得精确解，但是迭代法则需要给定误差限来确定核算终止迭代。