机器学习（matlab版）| lesson 3 非监督学习（cluster）

非监督学习：只有data，没有标签，将其分类

一、硬聚类

K-means

K:所分的类别数目  K=3，将data分成三类  C1 C2 C3

两个条件

1)C1+C2+...+Ck=data

2）任何两个C的交集是空集

一个好的分类要求：所分的三个集群尽可能均匀。

COST FUNCTION:

欧氏距离/直线距离

K均值聚类算法steps：

1） 随机将数据分成三个群

2）计算每个群的中心（均值）

3）重新分群，将距离中心近的分成一群

重复2） 3）进行迭代

ps:要避免陷入局部最优解

因为聚类的结果依赖于随机的初值，最后我们得到的有可能是一个局部最优解而非全局最优解

我们需要多次运行算法->多次赋不同的初值，选择最优的结果

%k-means
load fisheriris
K=3;%分成三类
%只训练一次，容易陷入局部最优解
[ind,C,sumd]=kmeans(meas,K);
%ind：类别号
%C：三个中心
%sumd:损失函数的Loss值

figure;hold on;
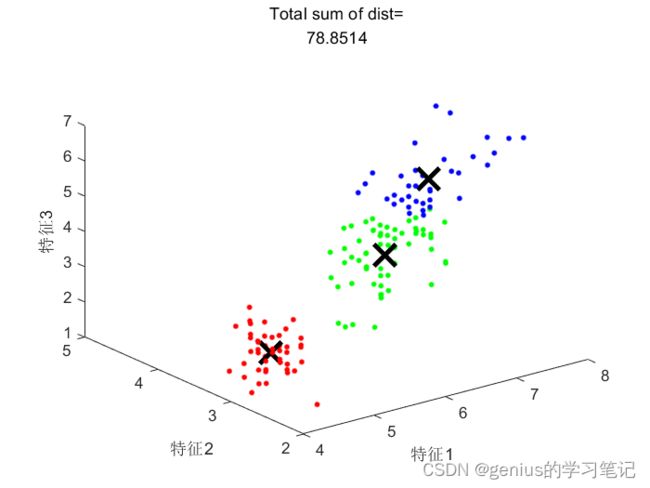
plot3(meas(ind==1,1),meas(ind==1,2),meas(ind==1,3),"r.","markersize",10);
plot3(C(1,1),C(1,2),C(1,3),"kx","markersize",20,"LineWidth",3);
plot3(meas(ind==2,1),meas(ind==2,2),meas(ind==2,3),"g.","markersize",10);
plot3(C(2,1),C(2,2),C(2,3),"kx","markersize",20,"LineWidth",3);
plot3(meas(ind==3,1),meas(ind==3,2),meas(ind==3,3),"b.","markersize",10);
plot3(C(3,1),C(3,2),C(3,3),"kx","markersize",20,"LineWidth",3);
view(3)
xlabel("特征1");ylabel("特征2");zlabel("特征3");
title(["Total sum of dist=",num2str(sum(sumd))]);
disp(["loss值为",num2str(sum(sumd))])

 调用函数多次kmeans

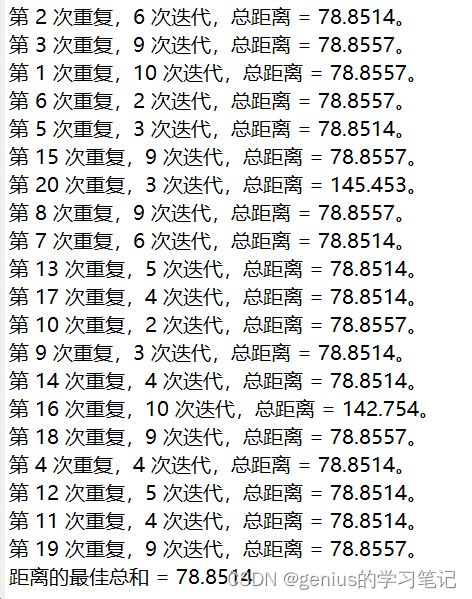
opts=statset('Display','final','UseParallel',1);
% opts=statset('UseParallel',1);
[ind,C,sumd]=kmeans(meas,K,'MaxIter',10000,...
    'Replicates',20,'Options',opts);

figure;hold on;
plot3(meas(ind==1,1),meas(ind==1,2),meas(ind==1,3),"r.","markersize",10);
plot3(C(1,1),C(1,2),C(1,3),"kx","markersize",20,"LineWidth",3);
plot3(meas(ind==2,1),meas(ind==2,2),meas(ind==2,3),"g.","markersize",10);
plot3(C(2,1),C(2,2),C(2,3),"kx","markersize",20,"LineWidth",3);
plot3(meas(ind==3,1),meas(ind==3,2),meas(ind==3,3),"b.","markersize",10);
plot3(C(3,1),C(3,2),C(3,3),"kx","markersize",20,"LineWidth",3);
view(3)
xlabel("特征1");ylabel("特征2");zlabel("特征3");
title(["Total sum of dist=",num2str(sum(sumd))]);

 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

Hierarchical Clustering（阶层式集群分析）

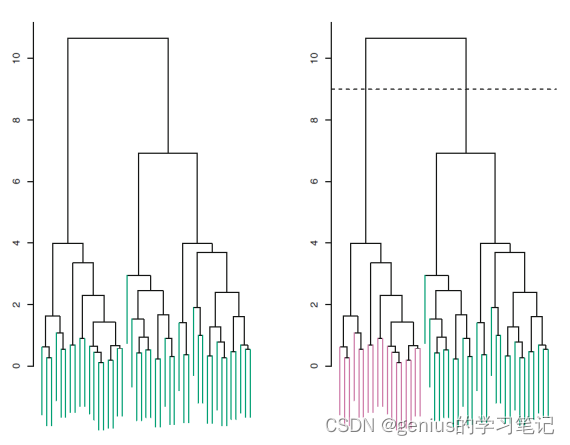
我们对K的值不是特别清楚，HC算法能帮助我们构建一个树状图

我们可以在不同高度“砍一刀”来分不同的类

 另外，越下面在一个树枝上说明二者越相似

HC算法

1）首先将所有数据都当做独立的组，分别计算互相的近似程度（欧氏距离），一共需要计算n(n-1)/2次

2)  For k=n,n-1,n-2,...,2:

a) 检测所有的k类集群，在它们之中找到最相近的两类，然后将这两个放到一起。

b) 在此计算新类的距离

重复迭代a 和b 

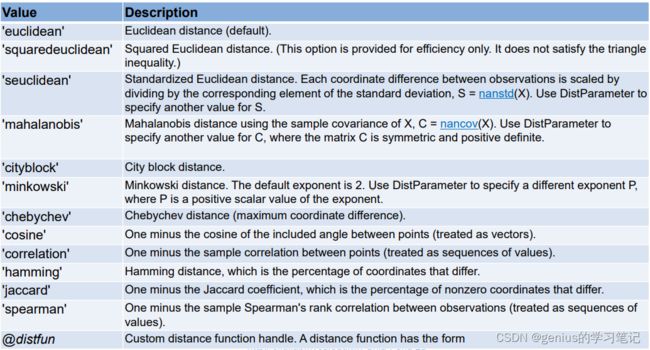
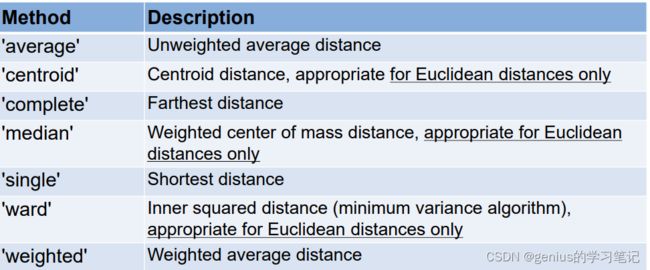
常用的计算距离的方式（matlab提供） 

'euclidean'通常比较常用

 ps:最后一个是自定义计算距离函数（当对数据集有更深刻认识的情况下可以这么做）

将数据合并了，如何计算新的组和其他数据的距离呢？

matlab提供了一些求算方式（linkage）

'average','complete','single'--比较常用

'average','complete'：看起来分布得更加均匀

'single'：结果可能比较零碎

linkage的选择也很重要

实例数据：

#NCI60数据集：60多种不同基因表现形的性状数据

close all;clc;clear all;

%数据读取
[numdata,CellLine,raw]=xlsread('NCI60data.csv');
%将第一行数据丢掉
numdata(1,:)=[];
%标准化数据,均值为0，方差为1
Z=zscore(numdata);

%HC算法的三个步骤
%1）pdist,计算相似度,每一行代表具体一个样本，每一列代表一个特征,计算出的数值越小表示越像
D=pdist(Z,'euclidean');
%2）linkage 连接
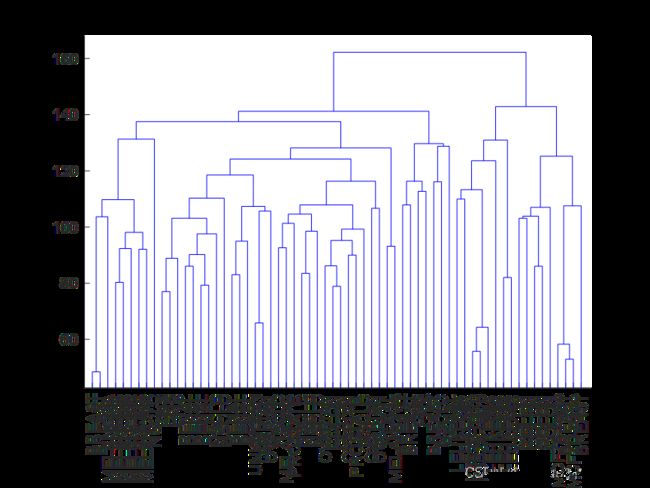
CT_complete=linkage(D,'complete');
figure;
%第二个参数是选择绘制数据的个数，如果是0代表全绘制，Label丢进去，不丢会显示数字不好看，最后那个参数改走向，top可以改成left
[H,T,outperm_complete]=dendrogram(CT_complete,0,'Labels',CellLine,'Orientation','top');
set(gca,'XTickLabelRotation',90);%将横轴标签转90度
title("complete")

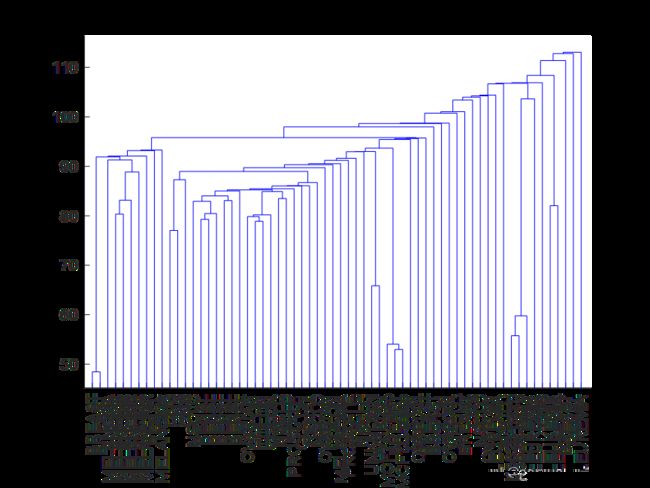
CT_avg=linkage(D,'average');
figure;
[H,T,outperm_avg]=dendrogram(CT_avg,0,'Labels',CellLine,'Orientation','top');
set(gca,'XTickLabelRotation',90);
title("average");

CT_sig=linkage(D,'single');
figure;
[H,T,outperm_sig]=dendrogram(CT_sig,0,'Labels',CellLine,'Orientation','top');
set(gca,'XTickLabelRotation',90);
title("single");

%3）cluster 砍树，决定分几类
K=5;
Clabel=cluster(CT_complete,"maxclust",K);

 

 

 二、软聚类

 提供额外的概率信息

比如说要分成三类，求算出每个样本分到三个集群的概率，比如说0.7,0.2,0.1

EA算法

最大化这个L，使得出现概率最大，但是uk和sigmak未知，我们要迭代求算

close all;clc;clear all;

%仿真数据
rng(0,'twister');
u1=[1 2];
sigma1=[3 .2;.2 2];
u2=[-1 -2];
sigma2=[2 0;0 1];
%生成 mvnrnd函数生成二维数据
X=[mvnrnd(u1,sigma1,200);mvnrnd(u2,sigma2,200)];

%绘制
figure;
plot(X(:,1),X(:,2),'k.',"markersize",10);
xlabel("feature 1");ylabel("feature 2");

%一个指令
K=2;
gm=fitgmdist(X,K);

%求算所有数据点的概率
P=posterior(gm,X);
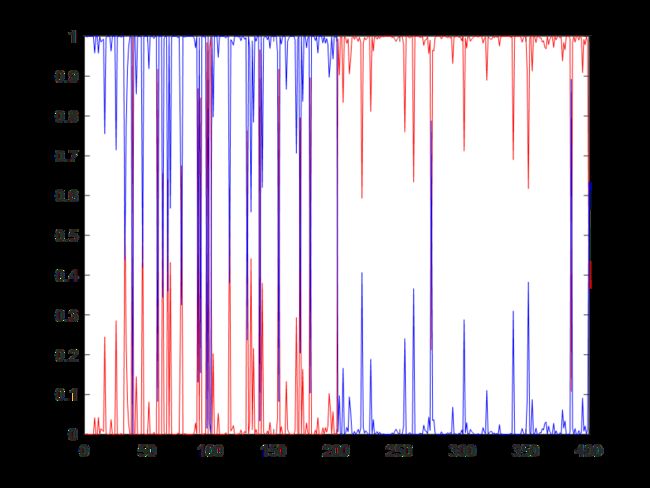
figure;
plot(P(:,1),'r');hold on;plot(P(:,2),'b');

label1=find(P(:,1)>0.6);
label2=find(P(:,1)<0.4);
label=find((P(:,1)>=0.4)&(P(:,1)<=0.6));
ind=cluster(gm,X);%硬聚类

%绘制
figure;
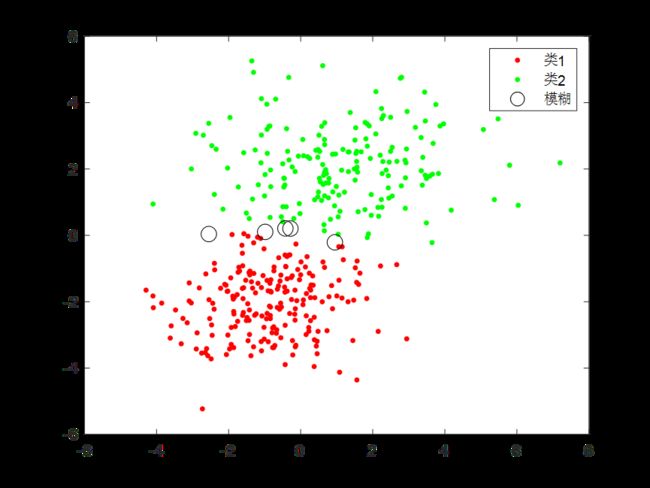
plot(X(label1,1),X(label1,2),'r.','markersize',10);hold on;
plot(X(label2,1),X(label2,2),'g.','markersize',10);hold on;
plot(X(label,1),X(label,2),'ko','markersize',10);hold on;
legend("类1","类2","模糊");

 总结：

核心指令就两个：

gm=fitgmdist(X,K),将数据X分成K类

P=posterior(gm)

其它操作都是为了实现数据可视化

在此，人工设定界限,P>0.6认为归类于1  P<0.4界定与类2；其它情况设定为模糊状态。

​​​​​​​