数字图像处理（三）空域增强+python

要求：

• 实现直方图均衡化的算法，对彩色图像进行直方图均衡化
• 彩色图像的去噪：对一副彩色图像分别添加高斯噪声和椒盐噪声； 编写一种线性滤波（如均值滤波）与一种非线性滤波（如中值滤波），对二种噪声图像进行去噪。
• 图像锐化：基于微分算子，编写程序实现一种锐化滤波，提取图像的边缘信息； 将上述步骤提取的图像，叠加到原图上，分析和比较锐化后的效果。

一、直方图均衡化

1.说明

直方图均衡化是对于一个图像，它有多个灰度级的像素，我们需要尽可能的让这些灰度级出现的频率相同。这样会有更好的对比度，细节展示的更好。作业1先计算当前直方图结果，然后再进行直方图均衡化，再显示出之后的直方图结果。

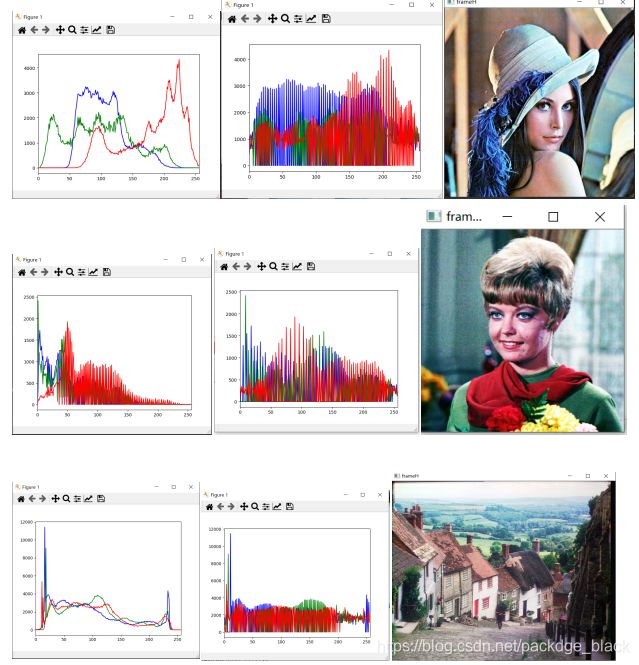
2.效果展示

采用3张图片，效果如下（从左到右依次为均衡前，均衡后，效果图）：

3.实验结果分析

可以从效果图中发现，均衡化之后的彩色图像，对比度增强了，细节也展示的更好了，虽然有的地方会出现色调的变化，就像LENA图，但是总体来讲还是很不错的。

4.代码

import os

import cv2
import numpy as np

import matplotlib.pyplot as plt

# 画出直方图
def channel_hist(image) :
    color =('b', 'g', 'r')  # 画笔颜色
    for i , color in enumerate(color):
        # 计算直方图
        # 第四个参数为直方图的灰度级数
        hist = cv2.calcHist([image], [i], None, [256], [0, 256])
        plt.plot(hist, color)
        plt.xlim([0, 256])
    plt.show()

# 直方图均衡化
# cv2.equalizeHist(img) 可以将输入图像进行图像均衡化处理
test = cv2.imread("goldhill.png")

# 通道分离，顺序BGR不是RGB
(b, g, r) = cv2.split(test)
# cv2.split函数分离出的B、G、R是单通道图像

# 图像直方图均衡化cv2.equalizeHist
bH = cv2.equalizeHist(b)
gH = cv2.equalizeHist(g)
rH = cv2.equalizeHist(r)

# 通道合并cv2.merge
frameH = cv2.merge((bH, gH, rH))

cv2.imshow('frameH', frameH)
channel_hist(test)
channel_hist(frameH)

二、彩色图像的去噪

1.说明

常用去噪方法：均值滤波、中值滤波、高斯滤波。

线性滤波使用均值滤波，非线性滤波使用中值滤波，对上述添加的两种噪声进行去噪。

 均值滤波对于图像中含有零均值下的高斯噪声或对图像尖锐性要求不高的情况下有很好的处理效果。但是它造成处于边缘的像素点变得模糊，丢失了最初图像的某些特征，对边缘特征的提取造成困难。

中值滤波是非线性滤波，很适合处理椒盐噪声。但是，由于边缘抖动，细节信息易被滤除，中值滤波用于细节丰富的图像时处理效果欠佳，同时不适用于处理高斯噪声。

2.效果展示

3.实验结果分析

和说明中的结果相似，两种滤波对两种不同的噪声有着不同的处理结果和其优势。中值滤波适合椒盐噪声，均值滤波适合高斯噪声。

4.代码

import numpy as np
import cv2

def Gauss(img, mean, sigma):
    image = np.array(img / 255, dtype=float)
    noise = np.random.normal(mean, sigma, image.shape)
    res = image + noise
    if res.min() < 0:
        low_clip = -1.
    else:
        low_clip = 0.
    res = np.clip(res, low_clip, 1.0)
    res = np.uint8(res * 255)
    return res

def sp(img, percetage):
    NoiseImg = img.copy()
    thres = 1 - percetage
    for i in range(img.shape[0]):
        for j in range(img.shape[1]):
            r = np.random.random()
            if r < percetage:
                NoiseImg[i, j, 0] = 0
                NoiseImg[i, j, 1] = 0
                NoiseImg[i, j, 2] = 0
            elif r > thres:
                NoiseImg[i, j, 0] = 255
                NoiseImg[i, j, 1] = 255
                NoiseImg[i, j, 2] = 255
            else:
                NoiseImg[i, j, :] = img[i, j, :]
    return NoiseImg


def medium(img, k = 3):
    res = img.copy()
    for i in range(int(k/2), img.shape[0]-int(k/2)):
        for j in range(int(k/2), img.shape[1]-int(k/2)):
            s1 = []
            s2 = []
            s3 = []
            for m in range(i - k // 2, i + k // 2 + 1):
                for n in range(j - k // 2, j + k // 2 + 1):
                    s1.append(img[m][n][0])
                    s2.append(img[m][n][1])
                    s3.append(img[m][n][2])
            s1.sort()
            res[i][j][0] = s1[(int(k * k // 2))]
            s2.sort()
            res[i][j][1] = s2[(int(k * k // 2))]
            s3.sort()
            res[i][j][2] = s3[(int(k * k // 2))]
    return res


if __name__ == "__main__":
    mean_filter = np.array([[1/9, 1/9, 1/9],
                            [1/9, 1/9, 1/9],
                            [1/9, 1/9, 1/9]])

    img = cv2.imread("goldhill.png")
    img_s = sp(img, 0.05)

    img_medium1 = medium(img_s)
    img_mean1 = cv2.filter2D(img_s, -1, mean_filter)

    img_g = Gauss(img, 0, 0.1)

    img_medium2 = medium(img_g)
    img_mean2 = cv2.filter2D(img_g, -1, mean_filter)

    cv2.imshow('add_sp',img_s) # 添加了椒盐噪声
    cv2.imshow('sp_medium1', img_medium1) # 中值滤波
    cv2.imshow('sp_mean1', img_mean1) # 均值滤波
    cv2.imshow('add_gauss', img_g) # 添加了高斯噪声
    cv2.imshow('gauss_medium2', img_medium2) # 中值滤波
    cv2.imshow('gauss_mean2', img_mean2) # 均值滤波

    cv2.waitKey(0)

三、图像锐化

1.说明

图像锐化主要用来增强图像的突变信息，图像的细节和边缘信息。

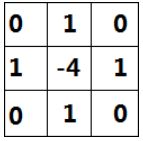
使用拉普拉斯算子进行图像锐化。

模板使用如下：

2.效果展示

3.实验结果分析

因为拉普莱斯算子，它的应用强调的是图像中的灰度突变，并不强调灰度级缓慢变化的区域。所以将原图像和拉普拉斯图像叠加在一起，就可以复原背景特性并保持拉普拉斯锐化处理的效果。

4.代码

import cv2
import numpy as np


def laplace(img):
    h = img.shape[0]
    w = img.shape[1]
    res = img.copy()
    L = np.array([[0, -1, 0],
                  [-1, 4, -1],
                  [0, -1, 0]])
    for i in range(h - 2):
        for j in range(w - 2):
            res[i + 1, j + 1] = abs(np.sum(img[i:i + 3, j:j + 3] * L))
    return np.uint8(res)


if __name__ == "__main__":

    img = cv2.imread("lena.tiff", 0)
    res = laplace(img)
    add=cv2.add(img,res)
    cv2.imshow('img', img)
    cv2.imshow('res',res)
    cv2.imshow('add',add)
    cv2.waitKey(0)