深度学习入门--感知机

单层感知机

数学表达式

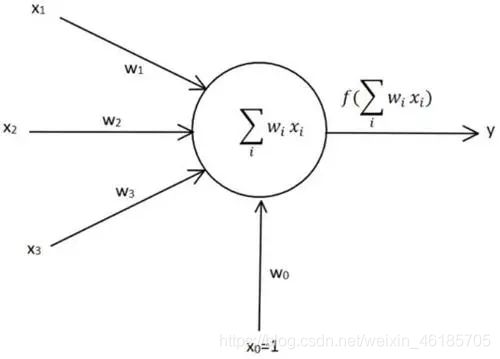
感知机是多个输入，一个输出，（0或者是1）的表达式
也可以理解为具有触发开关的神经元。

Y=0（W1X2+W2X2<=θ）
Y=1（W1X1+W2X2>θ）

W1,W2为权重 ，θ为某一个值

		   			图示

使用例子：与或非门，只是权重W1,W2不同，结果不一样。例子与门（W1=W2=0.5,输出为1，只有X1=X2=1时，才成立，也就是W1X1+W2X2=1）

逻辑电路的简单实现（与门）

def AND(x1,x2):
	w1,w2,theta=0.5,0.5,0.7
	tmp=x1*w1+x2*w2
	if(tmp<=theta):
		return 0
	elif tmp >theta:
		return 1
		
print(AND(0,0)) #0
print(AND(1,0)) #0
print(AND(1,1)) #1

导入权重和偏置

Y=0（W1X2+W2X2+B<=0）
Y=1（W1X1+W2X2+B>θ）

权重是控制输入信号的重要性的参数，偏置是调整神经元被激活的容易程度，偏置越大，输出1的概率越大。

逻辑电路的简单实现（与门/或门）

import numpy as np

def AND(x1,x2):
    x=np.array([x1,x2])
    w=np.array([-0.5,-0.5])
    b=-0.7
    tmp=np.sum(w*x)+b
    if tmp<=0:
        return 0
    else:
        return 1
#仅仅是权重不同 
def OR(x1,x2):
    x=np.array([x1,x2])
    w=np.array([0.5,0.5])
    b=-0.2
    tmp=np.sum(w*x)+b
    if tmp<=0:
        return 0
    else:
        return 1  
#非门             
def NAND(x1,x2):
    x=np.array([x1,x2])
    w=np.array([-0.5,-0.5])
    b=0.7
    tmp=np.sum(w*x)+b
    if tmp<=0:
        return 0
    else:
        return 1  

局限性

看数学表达式，可知，单层感知机是线性的，不能实现非线性的分割，因此不可以实现异或门。

多层感知机

多层感知机可以通过“叠加层”的方式来克服线性的问题，也就是可以通过这种方式实现异或门。

逻辑表达式：

根据表达式实现异或门

import numpy as np

def AND(x1,x2):
    x=np.array([x1,x2])
    w=np.array([-0.5,-0.5])
    b=-0.7
    tmp=np.sum(w*x)+b
    if tmp<=0:
        return 0
    else:
        return 1
#仅仅是权重不同 
def OR(x1,x2):
    x=np.array([x1,x2])
    w=np.array([0.5,0.5])
    b=-0.2
    tmp=np.sum(w*x)+b
    if tmp<=0:
        return 0
    else:
        return 1  
#非门             
def NAND(x1,x2):
    x=np.array([x1,x2])
    w=np.array([-0.5,-0.5])
    b=0.7
    tmp=np.sum(w*x)+b
    if tmp<=0:
        return 0
    else:
        return 1  

def XOR(x1,x2)    
	s1=NAND(x1,x2)
	s2=OR(x1,x2)
	y=AND(s1,s2)
	return y

这样就实现了3层的感知机，在上面例子中，无论是单层感知机还算多层感知机，都是需要手动确定权重和偏置，因此比较麻烦，这也是感知机的一个缺陷