李宏毅机器学习笔记p3-p4
文章目录
- 前言
- 一:Regression回归
-
- 1.线性模型
- 2.损失函数
- 3.梯度下降
- 二、验证模型好坏
-
- 过拟合
- 优化
-
- 1.模型的拆分
- 2.加入更多的参数,更多的input
- 3.正则化
- 三、代码的学习
- 总结
前言
经过上一篇章的学习,我们得知了有很多种深度学习,比如监督学习,无监督学习,强化学习等,监督学习算是深度学习的入门第一手,所以我们先学习监督学习中的回归
一:Regression回归
定义:前期学习(通过很多正确的输入和输出——>找到一个函数function),然后再输入特征x,输出一个结果。
步骤:
1.先选择模型
2.通过损失函数判断和结果的接近程度
3.通过梯度下降不断修正模型
1.线性模型
单个特征:
y = b + w x y = b + wx y=b+wx
多个特征:
y = b + ∑ w i x i y = b + \sum {{w_i}{x_i}} y=b+∑wixi
x:各种特征;w:各个特征的权重; b:偏移量。
多个特征——>联系到向量和矩阵,可以方便计算。
2.损失函数
作用:通过损失函数来评判模型的好坏
损失函数有很多种,一般是用均方误差和交叉熵误差等。
均方误差
E = 1 2 ∑ k ( y k − t k ) 2 E = \frac{1}{2}\sum\limits_k {{{({y_k} - {t_k})}^2}} E=21k∑(yk−tk)2
其中, E {E} E针对单个数据的损失函数, y k {y_k} yk表示神经网络的输出, t k {t_k} tk表示监督数据,k表示数据的维数。
交叉熵误差
E = − ∑ k t k log y k E = - \sum\limits_k {{t_k}\log {y_k}} E=−k∑tklogyk
其中, E {E} E针对单个数据的损失函数, y k {y_k} yk表示神经网络的输出, t k {t_k} tk表示正确解标签,只有正确解标签处的值才为1,其他都为0.
在老师讲课过程中,主要以均方误差来表示损失函数。
例如:统计10组原始数据 ( y ^ − f ( x n c p ) ) 2 {(\hat y - f({x^n}_{cp}))^2} (y^−f(xncp))2之和,和越小越好。
意思就是算出预测出来的值和真实的值的差越小越好。
L ( f ) = ∑ n = 1 10 ( y ^ n − f ( x n c p ) ) 2 L(f) = \sum\limits_{n = 1}^{10} {{{({{\hat y}^n} - f({x^n}_{cp}))}^2}} L(f)=n=1∑10(y^n−f(xncp))2
f ( x ) = y f(x) = y f(x)=y
y = b + w x c p y = b + w{x_{cp}} y=b+wxcp
将上文的三个式子总和可得最终损失函数Loss function:
L ( w , b ) = ∑ n = 1 10 ( y ^ n − f ( b + w x c p n ) ) 2 L(w,b) = \sum\limits_{n = 1}^{10} {{{({{\hat y}^n} - f(b + w{x_{cp}}^n))}^2}} L(w,b)=n=1∑10(y^n−f(b+wxcpn))2
拓展:此处 f ( x ) = y f(x) = y f(x)=y较为省略,更应该的是此处加一个激活函数,应更正为 f ( x ) = h ( y ) f(x) =h(y) f(x)=h(y)
3.梯度下降
为了使损失函数最小,结果更优,我们需要不断调整参数 ( w , b ) (w,b) (w,b),这里我们就用到梯度下降的方法。
先从只有一个参数w入手,任何可微分的L都可以
w ∗ = arg min x L ( w ) {w^*} = \arg \mathop {\min }\limits_x L(w) w∗=argxminL(w)
1.随机选出一个初始的点w0;
2.然后再计算切线斜率 d L d w ∣ w = w 0 \frac{{d{\rm{L}}}}{{d{\rm{w}}}}{|_{{\rm{w}} = {{\rm{w}}_0}}} dwdL∣w=w0,然后大于0往左移动,小于零往右移动。
3.跨步距离——学习率 η \eta η:事先定好的数值
4.移动: − η d L d w ∣ w = w 0 -\eta \frac{{d{\rm{L}}}}{{d{\rm{w}}}}{|_{{\rm{w}} = {{\rm{w}}_0}}} −ηdwdL∣w=w0
5.更新w0——> ω n + 1 = ω n − η d L d w ∣ w = w 0 {\omega _{n + 1}} = {\omega _n} - \eta \frac{{d{\rm{L}}}}{{d{\rm{w}}}}{|_{{\rm{w}} = {{\rm{w}}_0}}} ωn+1=ωn−ηdwdL∣w=w0
6.重复234.直到找到最低点
但是找到的只能说找到局部最小值而不是全局最小值。
两个参数:
同理,只不过是把导数变成偏导数。
∇ L = [ ∂ L ∂ w ∂ L ∂ b ] g r a d i e n t \nabla L = {\left[ {\begin{matrix}{} {\frac{{\partial L}}{{\partial w}}}\\ {\frac{{\partial L}}{{\partial b}}} \end{matrix}} \right]_{gradient}} ∇L=[∂w∂L∂b∂L]gradient
可以想想一个山坡,然后向最低的方向滚,然后通过往偏导方向走,那肯定是数值下降最快的方向。
但找到局部最优解,不一定是全局最优解。
但如果是在线性模型中,那肯定是局部最优解就是全局最优解。
二、验证模型好坏
过拟合
当有很多个数据点的时候,去拟合这个函数值。一元N次线性模型一般较为强大。
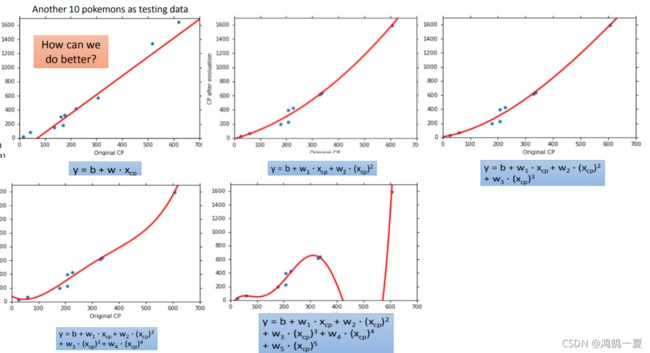
但是我们可以看到,并不是次数越高,就拟合效果越好,有时候过于追求每个点的精度,反而丢失了全局,造成过拟合问题。
优化
1.模型的拆分
将四个线性模型合并到一个线性模型中,只需要将对应模型板块的 δ \delta δ为1,不对应的为0,就可以避免混入其他线性模型中。
所以对于上文的线性拟合,如果知道其种类,把它分成三个线性模型,说不定可以得到更加精确的模型。
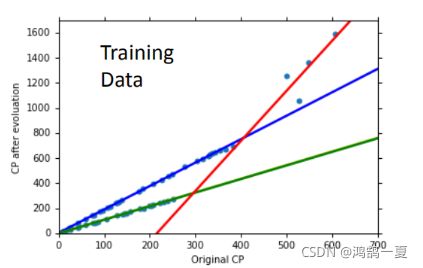
2.加入更多的参数,更多的input
设更多参数,加入更多input—>容易过拟合;
怎么办?
1.可以删掉相关性较小的input
2.加入正则化,重新定义我们的loss function
3.正则化
L = ∑ n ( y ^ n − ( b + ∑ w i x i ) ) 2 + λ ∑ ( w i ) 2 L = \sum\limits_n {{{({{\hat y}^n} - (b + \sum {{w_i}{x_i}} ))}^2} + \lambda \sum {{{({w_i})}^2}} } L=n∑(y^n−(b+∑wixi))2+λ∑(wi)2
加入 λ ∑ ( w i ) 2 {\lambda \sum {{{({w_i})}^2}} } λ∑(wi)2说明期望w越小越好
w越小越好——>比较平滑的——>output对输入的变化是不太敏感的。比较稳定——>可以避免一些干扰项的影响
λ \lambda λ越大的时候,说明我们越考虑函数的平滑。但也不能太平滑,所以我们需要不断的调整 λ \lambda λ
三、代码的学习
我于是对代码进行了研读。
用numpy的np.asarray来使列表变为数组。
我能理解lr的不断变动或许效果不是很好
所以将lr_b和lr_w分开
但我不大理解学习率用这种方式特化:
lr_b = lr_b + b_grad ** 2
lr_w = lr_w + w_grad ** 2
我想提前了解一下这种特化学习率的方法。
后经队长的指导,我了解到了原来是Adagrad方面的知识。
如果学习率固定,那针对不同的地方,学习率可能作用效果不同。
大致就是:
随着迭代次数增加,让学习率变小
初始迭代时,使用较大的学习率加速下降
迭代几次后,减小学习率防止振荡和越过
当然adagrad的相关知识之后也会学到,但是通过代码的调整,我提前了解到了adagrad的作用。在此感谢队长和相关伙伴的指导。
import numpy as np
import matplotlib.pyplot as plt
import time
from pylab import mpl
# matplotlib没有中文字体,动态解决
plt.rcParams['font.sans-serif'] = ['Simhei'] # 显示中文
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
#x_data正确输入数据 y_data 正确输出数据
x_data = [338., 333., 328., 207., 226., 25., 179., 60., 208., 606.]
y_data = [640., 633., 619., 393., 428., 27., 193., 66., 226., 1591.]
#用numpy将列表转化为数组
x_d = np.asarray(x_data)
y_d = np.asarray(y_data)
x = np.arange(-200, -100, 1)
y = np.arange(-5, 5, 0.1)
Z = np.zeros((len(x), len(y)))
X, Y = np.meshgrid(x, y)
# 求损失函数loss
for i in range(len(x)):
for j in range(len(y)):
b = x[i]
w = y[j]
Z[j][i] = 0 # meshgrid吐出结果:y为行,x为列
for n in range(len(x_data)):
Z[j][i] += (y_data[n] - b - w * x_data[n]) ** 2
Z[j][i] /= len(x_data)
# 线性回归
b = -120
w = -4
lr = 1
#迭代次数
iteration = 100000
b_history = [b]
w_history = [w]
#把w和b的学习率分来
lr_b = 0
lr_w = 0
start = time.time()
for i in range(iteration):
b_grad = 0.0
w_grad = 0.0
for n in range(len(x_data)):
b_grad = b_grad - 2.0 * (y_data[n] - n - w * x_data[n]) * 1.0
w_grad = w_grad - 2.0 * (y_data[n] - n - w * x_data[n]) * x_data[n]
#不理解???lr_b的变动
lr_b = lr_b + b_grad ** 2
lr_w = lr_w + w_grad ** 2
# update param
b -= lr / np.sqrt(lr_b) * b_grad
w -= lr / np.sqrt(lr_w) * w_grad
b_history.append(b)
w_history.append(w)
# plot the figure
plt.contourf(x, y, Z, 50, alpha=0.5, cmap=plt.get_cmap('jet')) # 填充等高线
plt.plot([-188.4], [2.67], 'x', ms=12, mew=3, color="orange")
plt.plot(b_history, w_history, 'o-', ms=3, lw=1.5, color='black')
plt.xlim(-200, -100)
plt.ylim(-5, 5)
plt.xlabel(r'$b$')
plt.ylabel(r'$w$')
plt.title("线性回归")
plt.show()
总结
提示:今天主要学习了回归里面的线性模型,损失函数,还有梯度下降。还学到了过拟合以及防止过拟合的正则化。但其讲的时候省略了激活函数这一块知识。还研读了一下其代码,在他人的帮助下提前对adagrqd对知识有了一定的了解。