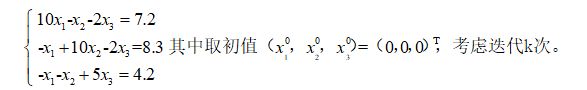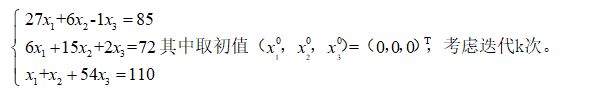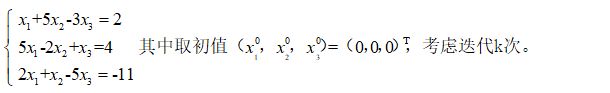线性方程组的数值解法

1 实验环境

Python实验环境

2 实验目的

掌握程序语言的基本知识，能够编写简单程序；

熟练掌握用Jacobi和Gauss-Seidel迭代法求线性方程组的问题。

3实验原理

4实验内容

1）实验方案

方案1、用Jacobi迭代法和Gauss-Seidel迭代法求解线性方程组）

思考：与教材结果比较。如果选取不同初值，会有影响吗？

方案2、用Jacobi迭代法和Gauss-Seidel迭代法求解线性方程组，要求精确到小数点后两位。

思考：考虑两种迭代法的收敛·性？.观察两种迭代法的收敛性性与收敛速度？观察比较并分析原因。

方案3、用Jacobi迭代法和Gauss-Seidel迭代法求解线性方程组，要求精确到小数点后两位。

思考：观察两种迭代法的收敛性性？观察比较并分析原因。如果是发散的，思考如何解决问题？

2）实验步骤

编写程序：

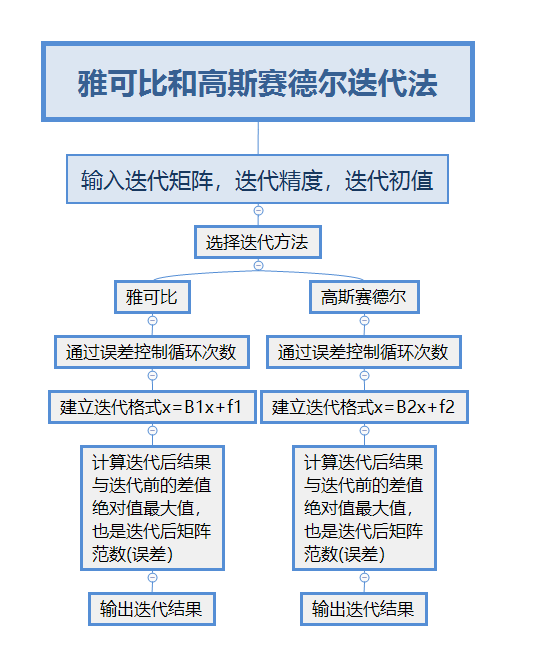
本次实验采用python进行编程，对于雅可比和高斯赛德尔迭代格式，其主要关键区别在于x^(k+1)与x^k。由于其系数矩阵，迭代精度，迭代初值均一样，所以我采用一个程序通过if判断选择迭代方法。程序大致框架如下。

迭代运算：

对于不同的题目，选择不同的系数矩阵，按照题目精度要求，初值要求进行迭代计算。

处理数据：

得出数据后，通过表格记录，收集数据并且处理数据。

5实验结论

方案一数据结论
结果	雅可比	赛德尔
e=0.000005X=[0，0，0]	迭代1次，x1=0.7200,x2=0.8300:x3=0.8400迭代2次，x1=0.9710,x2=1.0700:x3=1.1500迭代3次，x1=1.0570,x2=1.1571:x3=1.2482迭代4次，x1=1.0854,x2=1.1853:x3=1.2828迭代5次，x1=1.0951,x2=1.1951:x3=1.2941迭代6次，x1=1.0983,x2=1.1983:x3=1.2980迭代7次，x1=1.0994,x2=1.1994:x3=1.2993迭代8次，x1=1.0998,x2=1.1998:x3=1.2998迭代9次，x1=1.0999,x2=1.1999:x3=1.2999迭代10次，x1=1.1000,x2=1.2000:x3=1.3000迭代11次，x1=1.1000,x2=1.2000:x3=1.3000迭代12次，x1=1.1000,x2=1.2000:x3=1.3000迭代13次，x1=1.1000,x2=1.2000:x3=1.3000	迭代1次，x1=0.7200,x2=0.9020:x3=1.1644迭代2次，x1=1.0431,x2=1.1672:x3=1.2821迭代3次，x1=1.0931,x2=1.1957:x3=1.2978迭代4次，x1=1.0991,x2=1.1995:x3=1.2997迭代5次，x1=1.0999,x2=1.1999:x3=1.3000迭代6次，x1=1.1000,x2=1.2000:x3=1.3000迭代7次，x1=1.1000,x2=1.2000:x3=1.3000迭代8次，x1=1.1000,x2=1.2000:x3=1.3000
e=0.000005X=[1,1,1]	迭代1次，x1=1.0200,x2=1.1300:x3=1.2400迭代2次，x1=1.0810,x2=1.1800:x3=1.2700迭代3次，x1=1.0920,x2=1.1921:x3=1.2922迭代4次，x1=1.0977,x2=1.1976:x3=1.2968迭代5次，x1=1.0991,x2=1.1991:x3=1.2991迭代6次，x1=1.0997,x2=1.1997:x3=1.2997迭代7次，x1=1.0999,x2=1.1999:x3=1.2999迭代8次，x1=1.1000,x2=1.2000:x3=1.3000迭代9次，x1=1.1000,x2=1.2000:x3=1.3000迭代10次，x1=1.1000,x2=1.2000:x3=1.3000迭代11次，x1=1.1000,x2=1.2000:x3=1.3000	迭代1次，x1=1.0200,x2=1.1320:x3=1.2704迭代2次，x1=1.0873,x2=1.1928:x3=1.2960迭代3次，x1=1.0985,x2=1.1991:x3=1.2995迭代4次，x1=1.0998,x2=1.1999:x3=1.2999迭代5次，x1=1.1000,x2=1.2000:x3=1.3000迭代6次，x1=1.1000,x2=1.2000:x3=1.3000迭代7次，x1=1.1000,x2=1.2000:x3=1.3000
实验结论：通过数据比对，迭代初值不同，同精度下迭代次数也不同，同次数下迭代精度不同，但是迭代的结果不变。

方案二数据结论
结果	雅可比	赛德尔
e=0.5*10**(-2)X=[0，0，0]	迭代1次，x1=3.1481,x2=4.8000:x3=2.0370迭代2次，x1=2.1569,x2=3.2691:x3=1.8898迭代3次，x1=2.4917,x2=3.6852:x3=1.9366迭代4次，x1=2.4009,x2=3.5451:x3=1.9226迭代5次，x1=2.4316,x2=3.5833:x3=1.9269迭代6次，x1=2.4232,x2=3.5705:x3=1.9257迭代7次，x1=2.4260,x2=3.5740:x3=1.9260	迭代1次，x1=3.1481,x2=3.5407:x3=1.9132迭代2次，x1=2.4322,x2=3.5720:x3=1.9258迭代3次，x1=2.4257,x2=3.5729:x3=1.9260迭代4次，x1=2.4255,x2=3.5730:x3=1.9260
实验结论：雅可比迭代法求解此方程组收敛，迭代次数为7。高斯赛德也收敛，迭代次数为4；对比可以发现，求解此方程组，两种方法均收敛，高斯赛德尔迭代法比雅可迭代法收敛速度更快。原因是高斯赛德尔迭代时用代替。

方案三数据结论
结果	雅可比	赛德尔
B=[[1,5,-3,2],[5,-2,1,4],[2,1,-5,-11]]	迭代588次，x1=inf,x2=inf:x3=inf迭代589次，x1=nan,x2=inf:x3=inf	迭代315次，x1=77045919496045992896952013647348585254713962180759995434838328829224573182220312010704212682128377313280042437809756882541436612076863168895679775480347768173433462465595768619656582018675122239696889245544400276997914787039435852016622131657756367762007823274971904144532117140960509710937772666251963793408.0000,x2=inf:x3=inf迭代316次，x1=nan,x2=nan:x3=nan
B=[[5,-2,1,4],[1,5,-3,2],[2,1,-5,-11]]	迭代1次，x1=0.8000,x2=0.4000:x3=2.2000迭代2次，x1=0.5200,x2=1.5600:x3=2.6000迭代3次，x1=0.9040,x2=1.8560:x3=2.7200迭代4次，x1=0.9984,x2=1.8512:x3=2.9328迭代5次，x1=0.9539,x2=1.9600:x3=2.9696迭代6次，x1=0.9901,x2=1.9910:x3=2.9736迭代7次，x1=1.0017,x2=1.9861:x3=2.9942迭代8次，x1=0.9956,x2=1.9962:x3=2.9979迭代9次，x1=0.9989,x2=1.9996:x3=2.9975	迭代1次，x1=0.8000,x2=0.2400:x3=2.5680迭代2次，x1=0.3824,x2=1.8643:x3=2.7258迭代3次，x1=1.0006,x2=1.8354:x3=2.9673迭代4次，x1=0.9407,x2=1.9922:x3=2.9747迭代5次，x1=1.0020,x2=1.9844:x3=2.9977迭代6次，x1=0.9942,x2=1.9998:x3=2.9976迭代7次，x1=1.0004,x2=1.9985:x3=2.9999迭代8次，x1=0.9994,x2=2.0000:x3=2.9998
实验结论：在B=[[1,5,-3,2],[5,-2,1,4],[2,1,-5,-11]]情况下，两种方法都是发散的，将第一个方程和第二个方程交换位置，再利用用雅可比和高斯赛德尔迭代法求解都是收敛的。

源码：

方案1、用Jacobi迭代法和Gauss-Seidel迭代法求解线性方程组

程序

while True:     B=[[10,-1,-2,7.2],[-1,10,-2,8.3],[-1,-1,5,4.2]]     X=[0,0,0]#初值0     k=0     a=eval(input('请输入数字：'))#0雅可比，1赛德尔     e=eval(input('请输入精度：'))     c=100     if a==0:         while c>e:             XX = [0, 0, 0]             for i in range(3):                 XX[i] = 1 / B[i][i] * (B[i][3] - B[i][(i + 1) % 3] * X[(i + 1) % 3] - B[i][(i + 2) % 3] * X[(i + 2) % 3])             c=max(abs(XX[0]-X[0]),abs(XX[1]-X[1]),abs(XX[2]-X[2]))             X = XX             k=k+1             print('迭代{:}次，x1={:.4f},x2={:.4f}:x3={:.4f}'.format(k,X[0], X[1], X[2]))     else:         while c>e:             XX=X.copy()             for i in range(3):                 X[i] = 1 / B[i][i] * (B[i][3] - B[i][(i + 1) % 3] * X[(i + 1) % 3] - B[i][(i + 2) % 3] * X[(i + 2) % 3])             c = max(abs(XX[0] - X[0]), abs(XX[1] - X[1]), abs(XX[2] - X[2]))             k = k + 1             print('迭代{:}次，x1={:.4f},x2={:.4f}:x3={:.4f}'.format(k, X[0], X[1], X[2]))

结果	雅可比	赛德尔
e=0.000005X=[0，0，0]	迭代1次，x1=0.7200,x2=0.8300:x3=0.8400迭代2次，x1=0.9710,x2=1.0700:x3=1.1500迭代3次，x1=1.0570,x2=1.1571:x3=1.2482迭代4次，x1=1.0854,x2=1.1853:x3=1.2828迭代5次，x1=1.0951,x2=1.1951:x3=1.2941迭代6次，x1=1.0983,x2=1.1983:x3=1.2980迭代7次，x1=1.0994,x2=1.1994:x3=1.2993迭代8次，x1=1.0998,x2=1.1998:x3=1.2998迭代9次，x1=1.0999,x2=1.1999:x3=1.2999迭代10次，x1=1.1000,x2=1.2000:x3=1.3000迭代11次，x1=1.1000,x2=1.2000:x3=1.3000迭代12次，x1=1.1000,x2=1.2000:x3=1.3000迭代13次，x1=1.1000,x2=1.2000:x3=1.3000	迭代1次，x1=0.7200,x2=0.9020:x3=1.1644迭代2次，x1=1.0431,x2=1.1672:x3=1.2821迭代3次，x1=1.0931,x2=1.1957:x3=1.2978迭代4次，x1=1.0991,x2=1.1995:x3=1.2997迭代5次，x1=1.0999,x2=1.1999:x3=1.3000迭代6次，x1=1.1000,x2=1.2000:x3=1.3000迭代7次，x1=1.1000,x2=1.2000:x3=1.3000迭代8次，x1=1.1000,x2=1.2000:x3=1.3000
e=0.000005X=[1,1,1]	迭代1次，x1=1.0200,x2=1.1300:x3=1.2400迭代2次，x1=1.0810,x2=1.1800:x3=1.2700迭代3次，x1=1.0920,x2=1.1921:x3=1.2922迭代4次，x1=1.0977,x2=1.1976:x3=1.2968迭代5次，x1=1.0991,x2=1.1991:x3=1.2991迭代6次，x1=1.0997,x2=1.1997:x3=1.2997迭代7次，x1=1.0999,x2=1.1999:x3=1.2999迭代8次，x1=1.1000,x2=1.2000:x3=1.3000迭代9次，x1=1.1000,x2=1.2000:x3=1.3000迭代10次，x1=1.1000,x2=1.2000:x3=1.3000迭代11次，x1=1.1000,x2=1.2000:x3=1.3000	迭代1次，x1=1.0200,x2=1.1320:x3=1.2704迭代2次，x1=1.0873,x2=1.1928:x3=1.2960迭代3次，x1=1.0985,x2=1.1991:x3=1.2995迭代4次，x1=1.0998,x2=1.1999:x3=1.2999迭代5次，x1=1.1000,x2=1.2000:x3=1.3000迭代6次，x1=1.1000,x2=1.2000:x3=1.3000迭代7次，x1=1.1000,x2=1.2000:x3=1.3000

方案2、用Jacobi迭代法和Gauss-Seidel迭代法求解线性方程组，要求精确到小数点后两位。

程序

while True:     B=[[27,6,-1,85],[6,15,2,72],[1,1,54,110]]     X=[0,0,0]#初值0     k=0     a=eval(input('请输入数字：'))#0雅可比，1赛德尔     e=eval(input('请输入精度：'))     c=100     if a==0:         while c>e:             XX = [0, 0, 0]             for i in range(3):                 XX[i] = 1 / B[i][i] * (B[i][3] - B[i][(i + 1) % 3] * X[(i + 1) % 3] - B[i][(i + 2) % 3] * X[(i + 2) % 3])             c=max(abs(XX[0]-X[0]),abs(XX[1]-X[1]),abs(XX[2]-X[2]))             X = XX             k=k+1             print('迭代{:}次，x1={:.4f},x2={:.4f}:x3={:.4f}'.format(k,X[0], X[1], X[2]))     else:         while c>e:             XX=X.copy()             for i in range(3):                 X[i] = 1 / B[i][i] * (B[i][3] - B[i][(i + 1) % 3] * X[(i + 1) % 3] - B[i][(i + 2) % 3] * X[(i + 2) % 3])             c = max(abs(XX[0] - X[0]), abs(XX[1] - X[1]), abs(XX[2] - X[2]))             k = k + 1             print('迭代{:}次，x1={:.4f},x2={:.4f}:x3={:.4f}'.format(k, X[0], X[1], X[2]))

结果	雅可比	赛德尔
e=0.5*10**(-2)X=[0，0，0]	迭代1次，x1=3.1481,x2=4.8000:x3=2.0370迭代2次，x1=2.1569,x2=3.2691:x3=1.8898迭代3次，x1=2.4917,x2=3.6852:x3=1.9366迭代4次，x1=2.4009,x2=3.5451:x3=1.9226迭代5次，x1=2.4316,x2=3.5833:x3=1.9269迭代6次，x1=2.4232,x2=3.5705:x3=1.9257迭代7次，x1=2.4260,x2=3.5740:x3=1.9260	迭代1次，x1=3.1481,x2=3.5407:x3=1.9132迭代2次，x1=2.4322,x2=3.5720:x3=1.9258迭代3次，x1=2.4257,x2=3.5729:x3=1.9260迭代4次，x1=2.4255,x2=3.5730:x3=1.9260

方案3、用Jacobi迭代法和Gauss-Seidel迭代法求解线性方程组，要求精确到小数点后两位。

程序

while True:     B=[[1,5,-3,2],[5,-2,1,4],[2,1,-5,-11]]     X=[0,0,0]#初值0     k=0     a=eval(input('请输入数字：'))#0雅可比，1赛德尔     e=eval(input('请输入精度：'))     c=100     if a==0:         while c>e:             XX = [0, 0, 0]             for i in range(3):                 XX[i] = 1 / B[i][i] * (B[i][3] - B[i][(i + 1) % 3] * X[(i + 1) % 3] - B[i][(i + 2) % 3] * X[(i + 2) % 3])             c=max(abs(XX[0]-X[0]),abs(XX[1]-X[1]),abs(XX[2]-X[2]))             X = XX             k=k+1             print('迭代{:}次，x1={:.4f},x2={:.4f}:x3={:.4f}'.format(k,X[0], X[1], X[2]))     else:         while c>e:             XX=X.copy()             for i in range(3):                 X[i] = 1 / B[i][i] * (B[i][3] - B[i][(i + 1) % 3] * X[(i + 1) % 3] - B[i][(i + 2) % 3] * X[(i + 2) % 3])             c = max(abs(XX[0] - X[0]), abs(XX[1] - X[1]), abs(XX[2] - X[2]))             k = k + 1             print('迭代{:}次，x1={:.4f},x2={:.4f}:x3={:.4f}'.format(k, X[0], X[1], X[2]))

结果	雅可比	赛德尔
B=[[1,5,-3,2],[5,-2,1,4],[2,1,-5,-11]]	迭代588次，x1=inf,x2=inf:x3=inf迭代589次，x1=nan,x2=inf:x3=inf	迭代315次，x1=77045919496045992896952013647348585254713962180759995434838328829224573182220312010704212682128377313280042437809756882541436612076863168895679775480347768173433462465595768619656582018675122239696889245544400276997914787039435852016622131657756367762007823274971904144532117140960509710937772666251963793408.0000,x2=inf:x3=inf迭代316次，x1=nan,x2=nan:x3=nan
B=[[5,-2,1,4],[1,5,-3,2],[2,1,-5,-11]]	迭代1次，x1=0.8000,x2=0.4000:x3=2.2000迭代2次，x1=0.5200,x2=1.5600:x3=2.6000迭代3次，x1=0.9040,x2=1.8560:x3=2.7200迭代4次，x1=0.9984,x2=1.8512:x3=2.9328迭代5次，x1=0.9539,x2=1.9600:x3=2.9696迭代6次，x1=0.9901,x2=1.9910:x3=2.9736迭代7次，x1=1.0017,x2=1.9861:x3=2.9942迭代8次，x1=0.9956,x2=1.9962:x3=2.9979迭代9次，x1=0.9989,x2=1.9996:x3=2.9975	迭代1次，x1=0.8000,x2=0.2400:x3=2.5680迭代2次，x1=0.3824,x2=1.8643:x3=2.7258迭代3次，x1=1.0006,x2=1.8354:x3=2.9673迭代4次，x1=0.9407,x2=1.9922:x3=2.9747迭代5次，x1=1.0020,x2=1.9844:x3=2.9977迭代6次，x1=0.9942,x2=1.9998:x3=2.9976迭代7次，x1=1.0004,x2=1.9985:x3=2.9999迭代8次，x1=0.9994,x2=2.0000:x3=2.9998