神经网络:神经网络模型基础概念学习
1、数据集基本概念
训练集:是模型G实际接收到的数据。通常来说,为了使模型能在未知数据上表现得更好(也就是所谓的“泛化能力”更好),通常只会读取数据集的一部分作为训练集。
交叉验证集:是模型G“能看不能用”的数据。具体而言,G使用训练集来训练,并会时不时观察一下它在交叉验证集上的表现来决定是否继续训练,以及是否需要调节它自身的设置。
测试集:是用来评估G的性能的数据,是G“看不到”的数据。具体而言,只有在使用训练集来训练G并使用交叉验证集来监督训练后,才回使用使用测试集来看看G的表现究竟如何。
.
2、神经网络结构
2.1 神经元结构
神经元:神经元可以看作一个计算与存储单元,一个完整的神经元由“运算模型”与“激励函数”两部分构成。

运算模型:即该神经元在输入数据与数据权重之间进行的运算,通常为线性模型: y=wx+b,其中x为样本特征,w为权重矩阵b为偏置项。
激励(激活)函数:其作用是加入“非线性”因素,以及根据不同训练目的的需要,进行数学函数映射。
.
2.2 神经网络结构
神经网络结构:一个神经网络结构由输入层、隐含层、输出层组成。
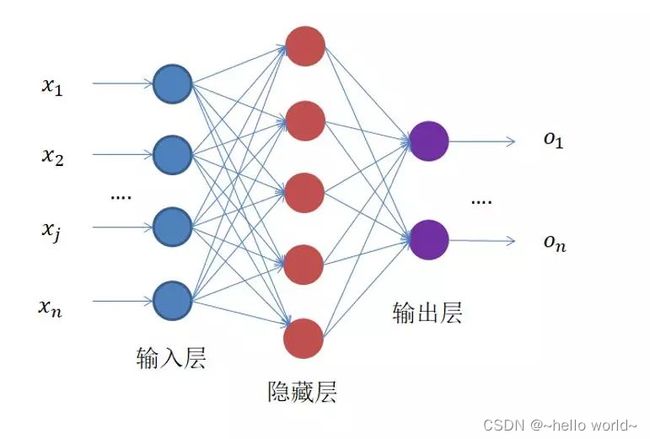
输入层:负责直接接受输入的数据,通常情况下不对数据做处理,也不计入神经网络的层数。
隐含层:是整个神经网络最为重要的部分,它可以是一层,也可是N层,隐含层的每个神经元都会对数据进行处理。
输出层:用来输出整个网络处理的值。
3、神经网络中的函数
3.1 激活函数
激活函数主要作用是对计算结果进行非线性变换,假如我们构建了一个多层的神经网络,那它每一层做的其实都是一个线性加权求和的运算,因此这个神经网络就只能做线性分类。当我们对每层网络中的各个节点都做非线性变换(使用激活函数)时,那么这个神经网络就可以做非线性分类任务了。
常用激活函数有Sigmoid激活函数、tanh激活函数、ReLu激活函数
Sigmoid函数
Sigmoid函数介于0~1之间,多用于输出层,常用作二分类。

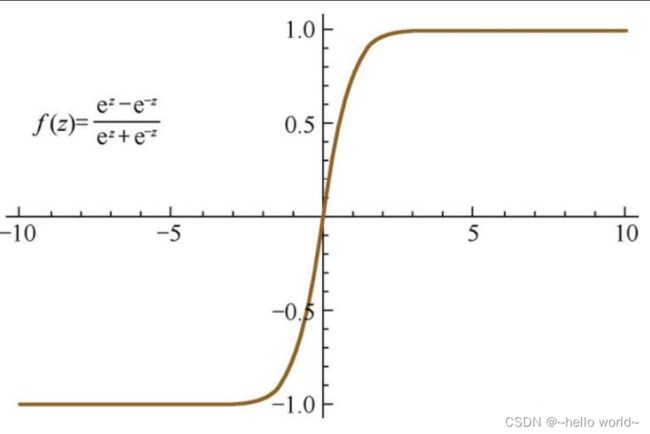
tanh激活函数
tanh函数(双曲正切函数)比Sigmoid函数表现得更好,它介于-1~1之间,激活函数的平均值就更接近0,多用于隐藏层。
ReLu激活函数
Sigmoid函数和tanh函数都有一个缺点,当自变量 x 非常大或非常小时,那么导数的梯度就很小,会严重影响梯度下降算法。ReLu函数(线性修正单元)解决了这个问题,当x大于0时,斜率为1;当x小于0时,斜率为0;当x等于0时,倒数没有意义。在实际生活中,当输出值为0和1或在做二分类时,那么Sigmoid函数很适合作为输出层的激活函数,其他所有层都用ReLu函数,能保证神经网络的学习速度。

LeakyReLU激活函数
ReLU 函数在 < 0时导数值恒为 0,也可能会造成梯度弥散现象,为了克服这个问题,LeakyReLU 函数被提出。中r为用户自行设置的某较小数值的超参数,如 0.02 等。当r =1时,LeayReLU 函数退化为 ReLU 函数;当r≠ 0时, < 0处能够获得较小的导数值r,从而避免出现梯度弥散现象。
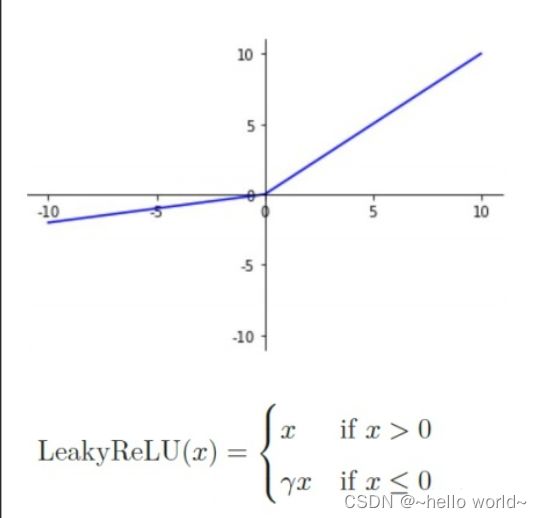
3.2 损失函数
损失函数是评估单个训练中预测值与真实值的接近程度,相当于预测值和真实值之间的误差,损失函数越小表明预测值与真实值更接近;神经网络训练或优化过程就是损失函数最小化的过程。
常用的损失函数有均方误差损失函数(MSE)、交叉熵损失函数(cross-entropy)、对数似然损失函数
均方误差损失函数(MSE)
#张量形式实现MSE
from tensorflow import keras
yi = tf.random.normal([2,10]) # 构造网络输出
y_onehot = tf.constant([1,3]) # 构造真实值
y_onehot = tf.one_hot(y_onehot, depth=10)
loss = keras.losses.MSE(y_onehot, yi) # 计算均方差
#MSE函数返回的是每个样本的均方差,需要在样本维度上再次平均来获得平均样本的均方差
loss = tf.reduce_mean(loss) # 计算样本均方差
print(loss)
tf.Tensor(1.6988729, shape=(), dtype=float32)
.
#层方式实现MSE
from tensorflow import keras
yi = tf.random.normal([2,10]) # 构造网络输出
y_onehot = tf.constant([1,3]) # 构造真实值
y_onehot = tf.one_hot(y_onehot, depth=10)
criteon = keras.losses.MeanSquaredError()
loss = criteon(y_onehot,yi) # 计算样本均方差
print(loss)
tf.Tensor(1.2020857, shape=(), dtype=float32)
.
交叉熵损失函数(cross-entropy)
在机器学习中,交叉熵能够衡量真实概率分布与预测概率分布之间的差异,交叉熵的值越小,模型预测效果就越好。交叉熵在分类问题中常常与softmax是标配,softmax将输出的结果进行处理,使其多个分类的预测值和为1,再通过交叉熵来计算损失。

其中,p(x)为真实概率分布,q ( x )为预测概率分布
.
对数似然损失函数
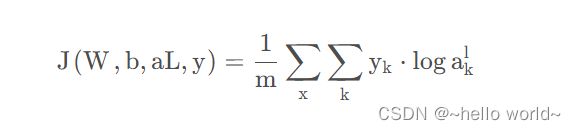
其中,(ak)^L表示网络的输出值,yk表示真值,取0或1。
.
4、梯度下降
梯度下降法的主要目的是通过迭代找到损失函数的最小值,或者收敛到最小值。
5、向量化
向量化计算是一种特殊的并行计算方式,可以简单理解为将普通运算转换成矩阵运算,向量化你的代码,会让程序运行得更快,常用向量化运算dot()来代替显式的for循环。
