利用numpy做图像旋转，以及对线性插值的个人理解

这是我第一次在CSDN上发表文章，如果文章有什么错漏之处敬请谅解。

前言

目前我正在就读数字媒体技术专业，需要涉及到图像处理和插值，这里我以图像旋转为例子来讲述一下numpy的简单使用和图像插值的做法，实际上，图像的放大，斜切等其他操作也可以套用这种方式
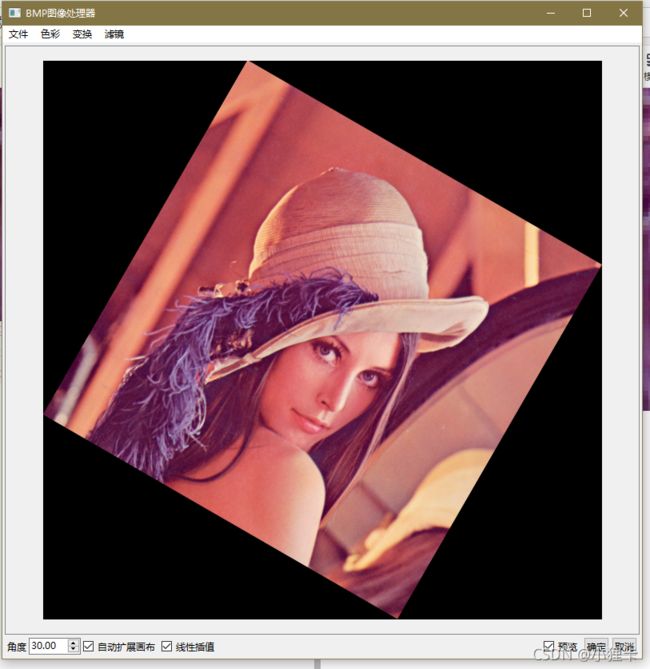
效果图如下：

获取旋转坐标矩阵

为了计算旋转后的坐标位置，我们需要获取到初始坐标。
这里以反变换为例子去做图像旋转，因为正变换几乎难以做插值，而且还要处理空穴。

计算结果图的尺寸

很简单，基本上高中数学知识就能算出来，注意计算之后要转换为整型。
$$\begin{gathered} wd=|\cos (\alpha )w{d}_0|+|\sin (\alpha )h{t}_0| \\ ht=|\cos (\alpha )w{d}_0|+|\sin (\alpha )h{t}_0| \end{gathered}$$

 wd = int(np.round(abs(cos(angle))*wd0+abs(sin(angle)*ht0)))
 ht = int(np.round(abs(sin(angle))*wd0+abs(cos(angle)*ht0)))

获取坐标矩阵

numpy提供了一个meshgrid(*xi, **kwargs)的方法用来生成坐标矩阵，对于图像处理来说，只需要提供两个一维序列作为参数即可。
在以下代码中i提供了点的x坐标，j提供了点的y坐标，值得注意的一点是坐标矩阵的shape是先行后列，与其他构造矩阵的方式略有不同。

>>> import numpy as np
>>> i = np.arange(0,8,1)
>>> j = np.arange(0,4,1)        #arange可以生成序列数组，类似于np.asarray(range(start,end,step))
>>> i
array([0, 1, 2, 3, 4, 5, 6, 7])
>>> j
array([0, 1, 2, 3])
>>> i,j = np.meshgrid(i,j)
>>> i
array([[0, 1, 2, 3, 4, 5, 6, 7],
       [0, 1, 2, 3, 4, 5, 6, 7],
       [0, 1, 2, 3, 4, 5, 6, 7],
       [0, 1, 2, 3, 4, 5, 6, 7]])
>>> j
array([[0, 0, 0, 0, 0, 0, 0, 0],
       [1, 1, 1, 1, 1, 1, 1, 1],
       [2, 2, 2, 2, 2, 2, 2, 2],
       [3, 3, 3, 3, 3, 3, 3, 3]])

移动轴心点

图像的旋转默认以(0,0)点作为旋转中心，即图像的左上角，但这并不是我们想要的，所以需要在构建旋转矩阵时把原点移动到中心，操作起来很简单，只需要在构建坐标矩阵之前减去半尺寸即可。

i = np.arange(0,wd,1)-wd//2
j = np.arange(0,ht,1)-ht//2
i,j = np.meshgrid(i,j)

效果类似于这样的感觉

>>> i
array([[-4, -3, -2, -1,  0,  1,  2,  3],
       [-4, -3, -2, -1,  0,  1,  2,  3],
       [-4, -3, -2, -1,  0,  1,  2,  3],
       [-4, -3, -2, -1,  0,  1,  2,  3],
       [-4, -3, -2, -1,  0,  1,  2,  3]])
>>> j
array([[-2, -2, -2, -2, -2, -2, -2, -2],
       [-1, -1, -1, -1, -1, -1, -1, -1],
       [ 0,  0,  0,  0,  0,  0,  0,  0],
       [ 1,  1,  1,  1,  1,  1,  1,  1],
       [ 2,  2,  2,  2,  2,  2,  2,  2]])

计算旋转坐标矩阵

旋转有两种思路
一种是正旋转，即从原图坐标变换到旋转后的坐标，正旋转的坐标表示旋转后的坐标
一种是反旋转，即从旋转后的坐标变换原图坐标，反旋转的坐标表示原图的坐标
由于我们并不知道旋转后的像素之间的关系，所以如果使用正旋转，会出现空穴
使用反旋转后，我们可以利用原图像素之间的关系来插值，以解决空穴
这里列出反旋转公式如下
$$\begin{gathered} i=i^{\prime }\ast \cos \alpha +j^{\prime }\ast \sin \alpha \\ j=-i^{\prime }\ast \sin \alpha +j^{\prime }\ast \cos \alpha \end{gathered}$$
反旋转的公式有很多文章已经做出证明，这里省略。
numpy的数组与常数相乘时会对数组逐项相乘，写代码还是挺方便的。
注意一定要用新的变量来接受结果值，否则可能会相互影响导致图像拉伸。

i = i1 * cos(angle) + j1 * sin(angle)
j = -i1 * sin(angle) + j1 * cos(angle)

把轴心点移动回去

前面的操作中轴心点的位置被移动到了中心，所以要移动回去。
由于我们已经通过反旋转公式将坐标矩阵转换为原图的坐标，所以这次需要加上原图的半尺寸才是正确的。

i = i + wd0//2
j = j + ht0//2

非法坐标的处理

对于超出原图范围的非法坐标，在生成图像时需要钳制到原图的坐标范围内，但如果不做处理的话会出现放射状边界。

在这里我提出了两种处理边界的方式

使用布尔矩阵记录非法坐标做遮罩

矩阵可以和常数或者同形状的矩阵做条件运算，返回值为布尔矩阵
值得注意的是numpy的矩阵并不支持python的区间比较的语法糖（如0 <= i < wd在numpy是不允许的），但是支持按位逻辑运算。
将布尔矩阵转换为任意形式的整型即可转换为01矩阵，将01矩阵与结果图相乘即可获得遮罩后的图像。

>>> mask = ((0 <= i) & (i < wd0) & (0 <= j) & (j < ht0)).astype(np.uint8)
>>> mask
array([[0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0],
       [0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0],
       [0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0],
       [0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
       [0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0],
       [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0],
       [1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0],
       [0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0],
       [0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0],
       [0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]], dtype=uint8)

注意彩图需要转换为RGB矩阵才能用，可以使用以下的代码升维并复制3份

mask = np.repeat(mask[:,:,np.newaxis],3,2)

效果如下，只能说勉强能用，但是边缘依然有锯齿

给原图添加一圈黑边

既然放射线是从图像的边缘发散出去的，那么只要图像的边缘是黑色的，黑色发散出去不就没有放射线了吗，而且黑边作为图像的一部分也可以和图像本身做插值解决图像边缘的锯齿问题。
代码也很简单，声明一个大一圈的0矩阵然后利用矩阵切片把原图数据插入进去即可

Extdata = np.zeros((ht0+2,wd0+2,3))
Extdata[1:ht0+1,1:wd0+1] = data
data = Extdata

注意由于长宽均增大了2个像素，所以对原点的修正相关代码也要修改（或者改wd0和ht0）

i = i + wd0//2 + 1
j = j + ht0//2 + 1

一句代码实现最近点插值

return data[np.clip(np.floor(j),0,ht0-1).astype(np.int32),np.clip(np.floor(i),0,wd0-1).astype(np.int32)].astype(np.uint8)

当然如果你看不懂的话可以看下面的分解版本，实际上只是多了个取整和钳制异常值的操作

i = np.floor(i).astype(np.int32)
j = np.floor(j).astype(np.int32)
i = np.clip(i,0,wd0-1)
j = np.clip(j,0,ht0-1)
return data[j,i].astype(np.uint8)

numpy具有非常强大的数组切片功能，这使得图像处理的代码可以完全矢量化，不需要使用循环，大大加快处理的速度。
注意i代表x坐标，j代表y坐标，而numpy的矩阵是先行后列，所以要j在前i在后。
也许有些人还是不太懂是什么意思，所以我们可以调试一下此处的代码看一下。

data.shape
(514, 514, 3)
data[j].shape
Evaluating: data[j].shape did not finish after 3.00 seconds.
(699, 699, 514, 3)
data[j,i].shape
(699, 699, 3)

还记得吗？i,j分别代表了变换前的的x坐标矩阵和y坐标矩阵，当坐标矩阵作为数组下标时，numpy会创建一个和矩阵同样大小的数组并提取对应位置的切片。
在这个例子里，j有699行699列，所以也会创建一个和j同样形状的数组，并且会根据j对应位置的值（y坐标）把data对应的行塞入到新数组内，相当于data[j]的第三维（长度为514的那一个维度）的值总是对应y坐标的整行像素。
data[j,i]后面的i会对data[j]做第二次筛选，注意第二个参数的形状一定要和第一个参数相同，此时会把整行像素的x坐标抽出来，得到一个点，此时data[j,i].shape为(699,699,1,3)，numpy会自动合并长度只有1的维度，最终将坐标矩阵转换为data上实际的像素点。
近邻法插值实现的效果如下，可以看出来毛边还是相当多的

2021年11月4日修订：
这里可以换一种方式来理解，就是把j,i联立成一个二维数组，然后作为下标取data的值并替换[j,i]的数据

小插曲：千万不要把下标写错了，虽然data[i][j]的写法通常情况下也能起到切片的作用，但是对于数组作为下标来说不适用，这种写法不会起到筛选作用，反而会将data[j]塞入到新数组中，于是data[j,i]的shape会变成
(699,699,699,514,3)
如果每一个数据占一个字节，则会占用526,642,496,658byte = 490.47GB

（网络图片，侵删）

线性插值的思路

获取权重矩阵

我总结了一个非常简单就能理解权重的方式：四个采样点的权重大小=对侧的矩形的面积：

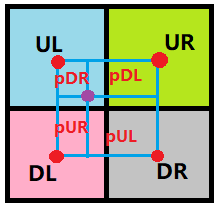
可以参考这篇文章：双线性插值算法的详细总结
这里提到了如果选择一个坐标系统使得 $f$ 的四个已知点坐标分别为 (0, 0)、(0, 1)、(1, 0) 和 (1, 1)，那么插值公式就可以化简如下，正好和我总结的对侧面积相同
（其实是我不太会用公式编辑器懒得写证明而已…）
$$f(x,y)\approx f(0,0)(1-x)(1-y)+f(1,0)x(1-y)+f(0,1)(1-x)y+f(1,1)xy$$
所以，为了计算权重，我们需要获取到四个采样点的坐标，这个获取起来很简单，只需要对坐标矩阵向下取整即可获得x0和y0的值，在此基础上加1即可获得x1和y1的值，通过对坐标的加减计算边长进而求出面积，即权重矩阵。
代码如下：

#坐标取整，左小右大，上小下大，通过这四个参数的组合得出四个采样点的坐标
iL = np.floor(i).astype(np.int32)
iR = iL+1
jU = np.floor(j).astype(np.int32)
jD = jU+1
#利用取整的坐标计算四个角的权重，注意RGB数组需要复制三份以向量化运算
pUL= (jD-j)*(iR-i);pUL=np.repeat(np.expand_dims(pUL,2),3,2)
pUR= (jD-j)*(i-iL);pUR=np.repeat(np.expand_dims(pUR,2),3,2)
pDL= (j-jU)*(iR-i);pDL=np.repeat(np.expand_dims(pDL,2),3,2)
pDR= (j-jU)*(i-iL);pDR=np.repeat(np.expand_dims(pDR,2),3,2)

一定要注意，不要使用np.ceil计算x1和y1，因为对于整数，floor和ceil的结果均为自身，这样计算权重时可能会出现负数，就会导致图片在某些角度下出现噪点。

计算插值后的图像

权重有了，四个采样点的坐标也有了，接下来我们就可以参照邻近插值的方式去计算线性插值的图像数据了
代码如下

#钳制点的范围
iL = np.clip(iL,0,wd0-1);iR = np.clip(iR,0,wd0-1)
jU = np.clip(jU,0,ht0-1);jD = np.clip(jD,0,ht0-1)
#权重与四个采样点求加权和
data = data[jU,iL]*pUL+data[jU,iR]*pUR+data[jD,iL]*pDL+data[jD,iR]*pDR
return data.astype(np.uint8)

这里建议先计算权重再钳制，以免边缘区域错误的权重导致出现锯齿

完整代码

Rotate(img:BMPFile,angle:float,islinear:bool,extend:bool)共有四个参数

• img:BMPFile:用来读取bmp文件信息的自定义图像类，其中BMPFile.data是一个RGB图像矩阵(shape=(ht0,wd0,3))
• angle:float:旋转的角度，以度为单位，所以需要处理成弧度才能用
• islinear:bool:是否使用线性过滤
• extend:bool:是否自动调整尺寸
  其中图像数据会被复制一遍以防止破坏原图

@staticmethod
def Rotate(img:BMPFile,angle:float,islinear:bool,extend:bool):
  tempimg = deepcopy(img)
  data = tempimg.data
  angle = radians(angle)
  wd0=tempimg.bmInfo.biWidth
  ht0=abs(tempimg.bmInfo.biHeight)
  #计算新图的尺寸
  if extend:
    wd = int(np.round(abs(cos(angle))*wd0+abs(sin(angle)*ht0)))
    ht = int(np.round(abs(sin(angle))*wd0+abs(cos(angle)*ht0)))
  else:
    wd=wd0;ht=ht0
  #旋转后的坐标系
  i1 = np.arange(0,wd,1)-wd//2
  j1 = np.arange(0,ht,1)-ht//2
  i1,j1 = np.meshgrid(i1,j1)
  #获取旋转前原图的坐标
  i = i1 * cos(angle) + j1 * sin(angle)
  j = -i1 * sin(angle) + j1 * cos(angle)
  #位置修正
  i = i + wd0//2 + 1
  j = j + ht0//2 + 1
  #加黑边
  Extdata = np.zeros((ht0+2,wd0+2,3))
  Extdata[1:ht0+1,1:wd0+1] = data
  data = Extdata
  #处理
  if(not islinear):
    tempimg.data = TranRotate.Nearly(data,i,j)
  else:
    tempimg.data = TranRotate.Linear(data,i,j)
  return tempimg 
  
#临近法
@staticmethod
def Nearly(data:np.ndarray,i:np.ndarray,j:np.ndarray):
  ht0,wd0 = data.shape[0],data.shape[1]
  ht,wd = i.shape
  i = np.floor(i).astype(np.int32)
  j = np.floor(j).astype(np.int32)
  i = np.clip(i,0,wd0-1)
  j = np.clip(j,0,ht0-1)
  return data[j,i].astype(np.uint8)
  
#插值法
@staticmethod
def Linear(data:np.ndarray,i:np.ndarray,j:np.ndarray):
  ht0,wd0 = data.shape[0],data.shape[1]
  ht,wd = i.shape
  #坐标取整，左小右大，上小下大，通过这四个参数的组合得出四个采样点的坐标
  iL = np.floor(i).astype(np.int32)
  iR = iL+1
  jU = np.floor(j).astype(np.int32)
  jD = jU+1
  #利用取整的坐标计算四个角的权重，注意RGB数组需要复制三份以向量化运算
  pUL= (jD-j)*(iR-i);pUL=np.repeat(np.expand_dims(pUL,2),3,2)
  pUR= (jD-j)*(i-iL);pUR=np.repeat(np.expand_dims(pUR,2),3,2)
  pDL= (j-jU)*(iR-i);pDL=np.repeat(np.expand_dims(pDL,2),3,2)
  pDR= (j-jU)*(i-iL);pDR=np.repeat(np.expand_dims(pDR,2),3,2)
  #钳制点的范围
  iL = np.clip(iL,0,wd0-1);iR = np.clip(iR,0,wd0-1)
  jU = np.clip(jU,0,ht0-1);jD = np.clip(jD,0,ht0-1)
  #权重与变换后的点相乘
  data = data[jU,iL]*pUL+data[jU,iR]*pUR+data[jD,iL]*pDL+data[jD,iR]*pDR
  return data.astype(np.uint8)

这个代码是我正在写的图像处理程序的一部分，图形界面基于PySide6编写（不过Qt方面我还是新手），如果大家感兴趣我也会把整个程序开源出来。

---

修订于2021-12-16日，对正旋转和反旋转做了区分，并修改了部分变量名以消除歧义