求勒让德n阶多项式、图像及求导 python实现

$$勒让德方程\frac{d}{dx}[(1-x^2)\frac{dy(x)}{dx}]+l(l+1)y(x)=0$$ $$勒让德多项式P_l(x)=\frac{1}{2^{l}l!}\frac{d^l}{d{x}^l}(x^2-1{)}^l$$
性质
1.正交性：

$${\int }_{-1}^1{P}_m(x)P_n(x)dx=\{\begin{array}{r}\frac{2}{2n+1},m=n\\ 0,m!=n\end{array}$$
2.递推关系
$$P_{n+1}(x)=\frac{2n+1}{n+1}x{P}_n(x)-\frac{n}{n+1}{P}_{n-1}(x)n=(1,2,...)$$

常用：
$$P_0(x)=1$$$$P_1(x)=x$$$$P_2(x)=(3x^2-1)/2$$$$P_3(x)=(5x^3-3x)/2$$

from sympy import *
x=symbols("x")
#legendre的n阶多项式
def legendre_polynomial(n):
    '''
    :param n: legendre多项式项数
    :return: legendre的n项展开
    '''

    P = [1, x]
    for i in range(1,n):
        m=(2*i+1)/(i+1)*x*P[i]-i/(i+1)*P[i-1]
        P.append(m)
    return P[n]

P_n=legendre_polynomial(3)
print(P_n)
#legendre的n阶多项式的m次导数
def Derivation(function,m):   #多阶求导
    """
    :param function : 待求导数的函数
    :param m: 求导阶数
    :return: legendre的n阶多项式的m次导数
    """
    for i in range(m):  #逐次求导  ，共m次
        derivation=diff(function,x)
        function=derivation
    return function

der=Derivation(P_n,2)
print(der)

结果：

legendre的n阶多项式: 1.66666666666667*x*(1.5*x**2 - 0.5) - 0.666666666666667*x
legendre的n阶多项式的m次导数: 15.0*x

绘制勒让德多项式图像以及legendre的n阶多项式的m次导数的图像：

from sympy import *
import matplotlib.pyplot as plt

x=symbols("x")
#legendre的n阶多项式
def legendre_polynomial(n):
    '''
    :param n: legendre多项式项数
    :return: legendre的n项展开
    '''

    P = [1, x]
    for i in range(1,n):
        m=(2*i+1)/(i+1)*x*P[i]-i/(i+1)*P[i-1]
        P.append(m)
    return P[n]
P_n=legendre_polynomial(3)
x1=[]
y1=[]
for i in range(200):
    x1.append(-1+0.01*i)
for i in x1:
    y1.append(P_n.subs('x',i))

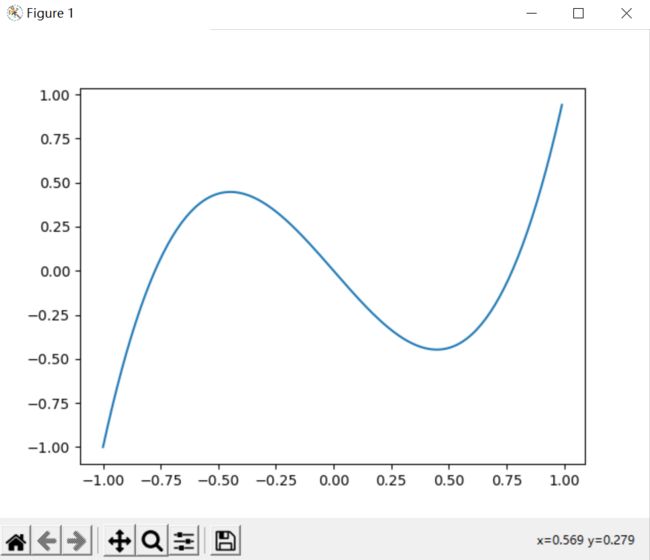
plt.plot(x1,y1)
plt.show()
#legendre的n阶多项式的m次导数
def Derivation(function,m):   #多阶求导
    """
    :param function : 待求导数的函数
    :param m: 求导阶数
    :return: legendre的n阶多项式的m次导数
    """
    for i in range(m):  #逐次求导  ，共m次
        f = diff(function, x, m)
    return f

der=Derivation(P_n,2)

y_value=[]
for i in x1:
    y_value.append(der.subs('x',i))

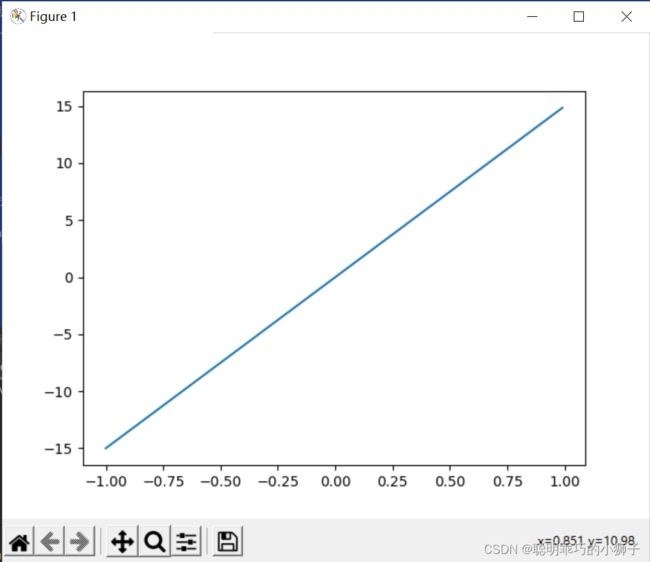
plt.plot(x1,y_value)
plt.show()

结果：

									3阶legendre多项式图像