归纳决策树ID3

使用ID3归纳决策树，根据新的气象指标数据判断是否去打球。

数据集weather.arff:

@relation weather
@attribute Outlook {Sunny, Overcast, Rain}
@attribute Temperature {Hot, Mild, Cool}
@attribute Humidity {High, Normal, Low}
@attribute Windy {FALSE, TRUE}
@attribute Play {N, P}
@data
Sunny,Hot,High,FALSE,N
Sunny,Hot,High,TRUE,N
Overcast,Hot,High,FALSE,P
Rain,Mild,High,FALSE,P
Rain,Cool,Normal,FALSE,P
Rain,Cool,Normal,TRUE,N
Overcast,Cool,Normal,TRUE,P
Sunny,Mild,High,FALSE,N
Sunny,Cool,Normal,FALSE,P
Rain,Mild,Normal,FALSE,P
Sunny,Mild,Normal,TRUE,P
Overcast,Mild,High,TRUE,P
Overcast,Hot,Normal,FALSE,P
Rain,Mild,High,TRUE,N

ID3算法

1、构造树的基本思想：

构造决策树的基本思想是随着树深度的增加，节点的熵迅速地降低，为了得到一课高度最矮的决策树，我们希望熵降低的速度越快越好。

2、计算信息熵：

已知weather.arff文件中，打球的概率是9/14，不打的概率是5/14。此时的熵为：

根据历史数据，属性outlook、temperature、humidity、windy在不同的取值下打球和不打球的次数统计如下：

outlook{（sunny:2P,3N），（overca：4P,0N），（rainy：3P,2N）}，

temperat{（hot：2P，2N），（mild：4P，2N），(cool:3P,1N)}，

humidity{(high:3P，4N)，（normal：6P，1N）}，

windy{（FALSE:6P，2N),(TRUE:3p,3N)},

已知变量outlook的值时，计算其信息熵：

outlook=sunny时，2/5的概率打球，3/5的概率不打球。

同理计算：

outlook=overcast时，Entropy=0

outlook=rainy时，Entropy=0.971

数据集中，outlook为sunny、overcast、rainy的概率分别是5/14、4/14、5/14，

所以变量outlook的信息熵为：5/14 × 0.971 + 4/14 × 0 + 5/14 × 0.971 = 0.693

此时，系统熵就从0.940降低到了0.693，

3、选取根节点：

同样的方法，计算出temperature、humidity、windy的信息增益，此时信息增益为：gain(outlook)=0.940-0.693=0.247>gain(humidity)=0.152>gain(windy)=0.048>gain(temperature)=0.029

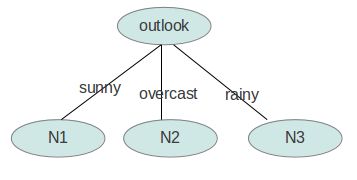
outlook的信息增益最大，它使系统的信息熵降低最快，所以决策树的根节点选取outlook。

4、建立决策树：

根节点选取后，如何确定N1取temperature、humidity还是windy?在已知outlook=sunny的情况，利用上述同样方法，根据历史数据，分别计算出信息增益gain(temperature)、gain(humidity)和gain(windy)，选最大者为N1。

依此类推，构造决策树，直到系统的信息熵降为0。