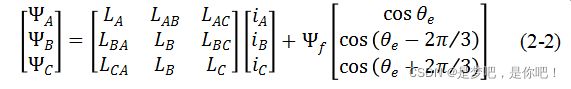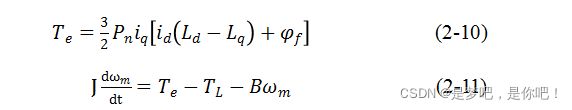永磁同步电机弱磁控制建模仿真

目录

1 绪论

1.1背景

1.2 永磁同步电机控制技术发展历史

1.3 弱磁控制的发展及现状

2 永磁同步电机的数学模型及控制技术 

2.1 永磁同步电机结构      ​

2.2 数学模型与矢量控制

2.2.1 abc三相静止坐标系下数学数学模型

2.2.2 αβ坐标系和dq坐标系模型及转换 

2.3 d-q坐标轴电流矢量图与MTPA控制

4 弱磁系统仿真模型及仿真结果  

4.1 弱磁控制数学模型

4.2 永磁同步电机弱磁调速系统仿真模型 

4.3 仿真结果及分析

4.3.1 仿真波形图

4.3.2 仿真结果分析

5 结论 

 参考文献

---

1 绪论

1.1背景

20世纪末，随着永磁同步电机在各个领域绽放光彩，永磁同步电机控制策略也得到了快速的发展。最开始是MTPA控制策略在永磁同步电机的恒转矩调速区的成功实现，这种方法大大的降低了电机和逆变器的损耗。而随着永磁同步电机在新能源汽车领域得到广泛应用后，人们对永磁同步电机控制策略的性能要求不断提高，需要支持电动汽车在不同环境下实现稳定高效的运行。于是对永磁同步单机的弱磁控制策略应运而生，并促使了永磁同步电机弱磁控制理论的不断发展和成熟。

永磁同步电机弱磁控制理论是在80年代中期，被以Brigette Sneyers和Thomas m. Jahns[1]为代表的的学者开创的，并且取得了卓越的成就。他们通过坐标变换把定子电流矢量从三相静止坐标系转换到了dq旋转坐标系，得到了id-iq电流矢量平面图。在d-q坐标系中分析了永磁同步电机的转矩和电流特性。在分析的基础上他们提出来控制定子电流工作点的弱磁思路，并且探究了d-q坐标系中电流MTPA曲线的确定方式。之后还分析了极限电压对工作点的约束和影响，当转速达到一定限度后，将导致工作点落到电压极限圆之外，这样定子侧的实际电流将无法跟踪上指令值。但当时那个时候弱磁控制还处在萌芽阶段，并不能详细全面的阐述弱磁控制理论及其本质规律。在之后的时间里，永磁同步电机弱磁调速策略慢慢走入人们的视野，并逐渐形成完善体系。今天，弱磁调速系统在各个领域中得到了广泛的使用，尤其是在电动汽车领域中取得了不可忽视的地位，也成为了电动汽车性能提升的重要研究方向之一[2]。

1.2 永磁同步电机控制技术发展历史

在控制技术还不够完善的初期，永磁同步电机控制技术还是以恒压频比控制（既u/f恒定）为主，这种方式是开环控制，不需要任何的反馈信号，所以有着简单的系统结构和低廉的成本[12-13]。不过开环控制也存在着弊端，就说难以实现高标准的稳定运行，电机的控制精度低且效率一般。正因为存在这些问题，所以恒压频比控制一般只能运用在风机、水泵等器械上。

在现代的闭环控制能够选择的控制方法之中，被广发接收的方法大致可以分为三种：矢量控制、模型预测控制和直接转矩控制，图1-1为同步电机一般的控制策略。

矢量控制（FOC）：在20世纪60年代，著名的德国学者Hasse正式第一次提出矢量控制理论。而德国学者Blasclke F[14]在1971年通过自己的理论研究，在他的论文中提出一个新的方向——利用矢量控制来解决电机的转矩控制问，也正是三相磁场控制理论的形成。矢量控制理论作为当今最耳熟能详的控制策略之一，其原理是将转子磁场定向，然后建立同步旋转的d-q坐标系，将旋转的三相电机数学模型转换成静止的两相数学模型。利用坐标变换能够将三相交流电转换成两相dq轴电流以达到解耦的目的，如此就能将交流电机的控制近似为直流电机控制，分别对励磁电流和转矩电流进行解耦控制，以达到电机调速驱动。

在各个领域被广泛接受的矢量控制可以主要是以下几种，最大转矩电流比控制（MTPA）是最主要也最常用的，其他还包括单位功率因数控制（cosθ=1）和id=0控制。单位功率因数控制是通过定子电流，使电机无功一直为0，也就是cosθ=1。系统不输出无功，能够大幅度提高效率节约能源。id=0控制是控制直轴去磁电流id为0，使得定子电流只剩下交轴分量id，如此就将直流去磁作用从电枢反应中剥离，避免由于直轴去磁电流带来的退磁现象。只需要控制交轴电流为所需值就可以得到需要的转矩，这样既降低了能力损耗也减小了电流，大大提高了效率。而最大转矩电流比控制最主要的思想就是在所需的电子转矩下找到能产生对应效果的最小定子电流，而凸极式的永磁同步电机控制方法大多数就是采取MTPA。通过对交、直轴电流分量的分别控制，就可以充分利用到d轴产生的磁阻转矩，使得电机和逆变器的损耗降低，以达到更高效的运行，而这也正好契合了电动车高转矩的要求。矢量控制能够做到对电机电流的精准控制，这有益于在矢量控制的基础上实现弱磁控制，这也是本文所重点研究的内容。

直接转矩控制（DTC）：在20世纪80年代，德国学者Depenbrock M和日本学者Takahashi I几乎同时提出了直接转矩控制策略，并将这种控制策略运用到了永磁同步电机控制中[15-16]。这种方式要求检测电机定子电压电流，并在ABC三相静止坐标系中实现电机的转矩和磁场的直接控制。通过这种直接控制避免了电流解耦的问题，不再需要像矢量控制那样将电流在不同坐标之间通过公式转换，控制系统也比较简单。不过也因此，直接转矩控制策略难以实现对电流的高精度控制，这也使得其不能实现更深层次的弱磁调速，这也大大限制了直接转矩控制的应用推广。

模型预测控制（MPC）：模型预测控制的概念早在20世纪70年代就已经提出，并且广泛的运用到了化工、石油等领域。但是模型控制理论运用到电机控制领域还是在数字电子和微处理器技术得到比较全面发展之后，直到2004年模型控制理论才正式运用到永磁同步电机控制。模型预测控制是反馈控制的一种，其控制原理是通过检测得到当前的被控对象输出量的测量值，并通过得到的测量值来设计模型，最后以模型来预测未来一段时间内被控对象的相关参数。只需要在之后不断重复这个过程，就能实现模型预测控制。模型预测控制能够实现多目标和多约束，而且其控制简单、稳定性好，在电机控制领域取得了不可忽视的地位，也成为了未来永磁同步电机控制的主要研究方向之一。

1.3 弱磁控制的发展及现状

永磁同步电机的转子上是永磁体，永磁体产生的磁场是固定不变的，所以无法通多改变其对应的磁场来调速。而直流的母线电压和直流电机相似，电压达到一定的限制之后是没办法再提高的，这也达到电压限制后导致不能再调压调速。所以为了能够扩大电机的调速范围，就必须采用弱磁调速（Flux-weaking,FW）来实现弱磁区的恒功率调速。电动汽车对电机的弱磁调速要求很高，需要达到一定的转速性能要求，甚至于电机的最高运行转速要达到基速的5倍以上。

表1-3 永磁同步电机弱磁控制方式比较

弱磁方法	优势	不足
开环控制	原理简单，直接规划电流轨迹	无参数鲁棒性，电机参数需要在线辨识：算法过程繁琐
查表法	结构简单；鲁棒性和动态响应能力较高；不依赖参数	数据标定工作量大，算法移植性差
电压幅值调节	不依赖电机参数；弱磁区间切换快速平滑	无法实现MTPV控制，深度弱磁区稳定性差
梯度下降	定子电流轨迹规划合理，能实现MTPV控制	算法复杂
单电流调节器	弱磁阶段对电压、电流进行调节的自由度一致，提高了深度	无法进行转矩控制，电机运行效率低，且只限于电动工况
混合式	动态性能好、鲁棒性高	极易出现过度修正，导致电机失控；使用场合有限

在Brigette Sneyers和Thomas m. Jahns等学者开创的PMSM弱磁调速萌芽阶段，虽然也对弱磁调速的做了粗略的介绍和分析，并且找到了弱磁调速控制的思路。但是由于那个时代的科技和技术的限制，当时的学者并不能对弱磁控制理论作出全面详细的解释。直到1990年日本学者Shigeo Morimoto[17]的出现，永磁同步电机的弱磁控制才得以系统化。他详细分析了弱磁控制在永磁同步电机中的使用，并且分析了控制过程中的各个阶段，按照转矩特性划分了三个工作区——恒转矩区、弱磁一区和弱磁二区。并且Morimoto按照划分的区域介绍了永磁同步电机的弱磁轨迹规划，推导出了相关的公式。随后，Morimot还引入了指令补偿器、电流解耦器等器件，用来提高弱磁调速的效率。这些工作也是奠定了弱磁控制的理论基础。

在弱磁调速理论提出之后，由于其对调速范围的大幅度提高，得到了各国学者的重视。直到今天，弱磁调速系统已经形成了完善的理论，并且在各个领域中得到了广泛的使用。而永磁同步电机的弱磁控制更是为电动汽车带来的新的活力，得到了快速的发展，现在永磁同步电机常用的弱磁控制方法包括如下几种：前馈开环控制法、查表法、电压幅值调节法、梯度下降法单电流调节器和混合式控制法。表1-3列举了永磁同步电机各种弱磁控制方法及比较，通过表中数据可以简单了解弱磁控制特点。

2 永磁同步电机的数学模型及控制技术 

2.1 永磁同步电机结构

          

                                            图2-1 永磁同步电机结构

         

图2-2 永磁同步电机转子结构

 如图2-1所示，PMSM主要的结构包括了转子、端盖、定子等部件。通过永磁同步电机的简单结构图2-1，可以看出带永磁铁的转子就是PMSM区别其他电机最大特点。对于一般的同步电机而言，产生永磁体相同作用的部件就是转子绕组，当直流电被通入到转子绕组，根据电磁理论就会产生恒定磁场，而定子绕组中会通入存在一定相角差的三相交流电，定子绕组就会产生旋转的磁场，两个磁场相互作用，就会带动转子同步旋转。而PMSM的永磁体会产生相同作用的恒定磁场来代替转子绕组作用。永磁同步电机分类主要是分为内嵌式和表贴式，两者的区别是永磁体安装在外壳内还是外壳外，如图2-2所示。而PMSM的定子部分和一般的感应电机差别并不大，主要作用是通入交流电后产生旋转磁场。

表贴式具有很多其他电机无法比拟的优势，包括其制造工艺相对简单且便利、转动惯性比比较小等等，这些优势都为其在工业上的广泛应用提供了条件。而且这种类型对于设计师进行更深层次的优化更加便利。不过表贴式的转矩相对而言就无法达到很大，在需要大转矩的场合解无法很好的嵌合。而内嵌式虽然结构相较而言比较复杂，但是其优点也是毋庸置疑的，由于其高气隙磁通密度的存在，内嵌式的电磁转矩可以达到很大。而且内嵌式的永磁体在转子内部，出现意外时风险可以降到最低，提高了其安全性能，也因此转子可以在更加高速的工况下安全运行。而内嵌式的这些优点都契合了电动汽车的生成要求，在电动汽车设计生产中被广泛使用，也是本论文的主要研究对象。

2.2 数学模型与矢量控制

对于永磁同步电机的研究，大多数的分析需要建立在数学模型之上，通过数学模型最终得到电机特性。但建立在abc三相静止坐标系的电机数学模型难以直接分析，一般通过坐标转换的方式将abc三相坐标系最终转换到d-q旋转坐标系，在d-q坐标系下进行相关的分析研究，就可以的到较为简单的表达式。坐标变换的的基本思想就是保证坐标变换前后的合成磁动势不变。

2.2.1 abc三相静止坐标系下数学数学模型

高阶和强耦合是永磁同步电机难以进行数学模型分析的重要原因，而要解决这个问题就需要实现模型上的简化，简化内容包括：1）忽略铁心饱和问题、2）忽略涡流、磁滞带来的电机运行损耗、3）忽略定子绕组参数变化。

abc三相静止坐标系下定子电压方程为：

     

其中：uA、uB、uC是定子绕组的相电压，RS是定子的电阻，iA、iB、iC是定子绕组相电流，ΨA、ΨB、ΨC是定子绕组的磁链。

三相定子磁链方程：

公式中LA、LAC、LBC、LCA等是三相定子绕组之间的互感和自感系数，θe是转子的电角度。

2.2.2 αβ坐标系和dq坐标系模型及转换 

建立在abc三相坐标系中的电机数学模型，由于电机中各个量都是交流量，具有时变的特性。而且各个物理量之间的关系非常复杂，难以实现数字化控制。于是选择相关的物理量进行坐标转换，根据磁动势相等的原则，在静止的α-β坐标系下可以找到对应电流产生相同磁场。在将α-β坐标系下转换到d-q旋转坐标系，得到解耦的电流分量iq、id。

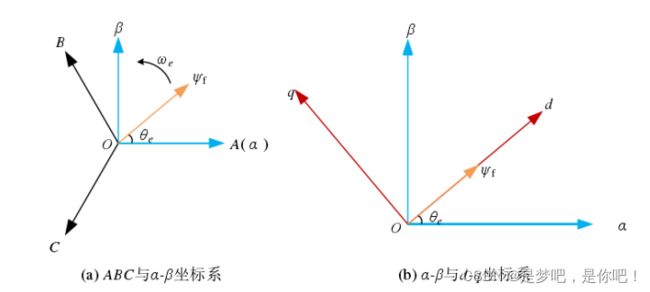
图2-2（a）是三相静止坐标系到静止α-β两相坐标系示意图。两个坐标的转换称为Clark变换与反Clark变换。方程如下：

     

                                            图2-3 坐标变换原理 

图2-2（b）描述了d-q旋转坐标系和α-β静止两相坐标系的示意图，二者的转换被称为Park转换与反Park变换，公式如下：

将公式（2-1）、（2-2）带入到公式（2-3）、（2-5）中进行坐标变换就可以得到d-q两相旋转坐标系下的电压方程：

式中：ud和uq是定子侧的电压；id和iq是定子侧的电流的d轴分量和q轴分量；Ld和Lq是定子侧电感的d轴分量和q轴分量；Ψd和Ψq是定子侧磁链的d轴分量和q轴分量；Ψf是永磁体磁链；R是定子的电阻；ωe为电角速度。

永磁同步电机的电磁转矩方程和机械运动方程：

式中：TL负载转矩、B阻尼系数、J转动惯量、Pn极对数、ωe转子机械角速度。

2.3 d-q坐标轴电流矢量图与MTPA控制

将abc三相坐标系中的电机数学模型转换到d-q两相旋转坐标系，得到了更简单的方程，这也为矢量控制提供了条件。矢量控制就是在d-q坐标系下对定子侧电流的d轴和q轴分量id、iq进行独立控制。图2-3即为d-q坐标系电流矢量图。

分析图2-4可知，图中的T1、T2都是等转矩曲线，当转矩曲线处在第二象限时代表的是电机向外输送转矩，也就是永磁同步电机处在电动状态，反之亦然。论文中主要分析的也是永磁电机的电动状态。电流矢量圆代表的是定子电流IS幅值相等的工作点的集合，其表达式是：

                 

图2-4 d-q轴电流矢量图

最大转矩电流控制是最常见的永磁同步电机控制之一，主要原理就是找到最小的电流产生最大的转矩，是高效且节能的电流控制法。由图2-4可以看出，对于每一个给定的电磁转矩Te，图中都有无数个工作点（id，iq）能够产生相应的转矩，而每一个工作点都对应于一个电流矢量Is，而最大转矩电流比控制则是找到所有有效的工作电流Is中幅值最小（离原点最近）的点。体现在图2-3中就是每个恒转矩曲线与电流矢量圆相切工作点。如果给定一系列连续的恒转矩曲线，则每个恒转矩曲线都有一个与矢量圆的切点，而这些切点的集合就是图中所示的MTPA轨迹曲线。在这条曲线上的工作点都是产生对应转矩需要的最小电流，可以减小能量消耗和电机损耗，有利于提高系统的效率和寿命。以下是MTPA曲线推导过程。

MTPA是找到对应转矩产生所需要的最小电流，可以转换为求取式（2-12）条件下，式（2-10）的极值问题。引入拉格朗日极值辅助函数：

id和iq的解析式求解出来比较复杂，而且现实情况一般更为复杂，通过计算找到轨迹的方法比较难以实现，所以我们一般会采用查表法或者曲线拟合法。 

4 弱磁系统仿真模型及仿真结果  

对于永磁同步电机的控制，由图3-3可知，当速度低于基速ωe时，电机是处于恒转矩区，采用的控制方式是MTPA。此时电压极限椭圆并不会对电流造成限制，电流矢量只需保持在电流极限圆内，通过MTPA就可以找到对应转矩所需要的最小电流，最大转矩电流比控制的工作点的集合即为如图所示的MTPA曲线。如图3-4当速度大于基速ωe时，最大转矩电流比工作点A落在了电压极限椭圆以外，无法再通过最大转矩电流比控制，此时为了得到最大的转矩，将A点沿着左下方位置移动，直到电压极限椭圆和电流极限圆的交点B点，得到转矩TB，此过程就是通过电流dq轴分量id、iq实现的弱磁控制。

4.1 弱磁控制数学模型

当电机转速还没有达到基速时，永磁同步电机采用最大转矩电流比控制，当电流达到极限电流Ilim时，电动机的id和iq分别为：

4.2 永磁同步电机弱磁调速系统仿真模型 

在Matlab2015b的Simulink环境下，利用所带的丰富的模块库，通过d-q坐标系下的矢量空间运行轨迹和弱磁数学控制模型，提出了永磁同步电机弱磁控制模型搭建策略，所搭建的弱磁仿真模型如图4-1所示。

         

                          图4-1 永磁同步电机弱磁调速系统仿真模型

       

4-2 弱磁调速模块和MTPA模块

由图4-1可知，所搭建的PMSM弱磁控制模型以电流反馈作为内环和转速反馈作为外环。整个系统包括矢量控制模块、弱磁控制模块、PI调节器、解耦模块、电源模块、MTPA模块等等。外环是转速负反馈，给定转速，将给定转速和实际反馈转速的差值作为控制信号输入，之后输入信号通过PI调节器和MTPA模块作用得到交轴和直轴在给定转速下的电流分量参考值id*和iq*。当弱磁模块判定电机电压超过极限电压，此时弱磁控制模块将会重新分配id和iq，就能分别得到新的交轴和直轴参考电流。所得到的参考电流与实际的反馈的电流一起组成电流内环，最后经过PI调节器输出控制电压ud和uq。控制电压在SVPWM模块中产生对应的控制波形，最终控制通用桥来控制电机的运行。

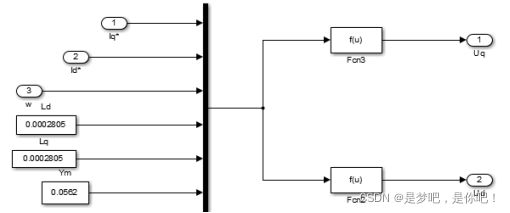
图4-2为MTPA模块和弱磁控制模块，通过d-q坐标系下的矢量空间的恒转矩区和弱磁Ⅰ区的轨迹规划和数学模型搭建，当转速没有达到基速只有MTPA工作，当转速达到基速后通过开关启动弱磁调速模块重新规划电流。所选择的模块包括：加法器、增益模块、公式Fcn模块、开关模块、积分器等等。子系统中的所使用的d轴、q轴电感设置为、，最大极限电压设置为。输入的电压ud和uq通过Fcn2得到电压矢量US，输入的角速度ω*通过Fcn3得到id2，所得到的US和id2通过加法器、减法器、积分和增益环节能够得到弱磁调速电流所需要的id，当电机的转速没有达到指定值3000时开关拨到，反之达到指定值后就会输出所求时id。iq输出则是通过Fcn2由id和输入ism计算得出。

模型中使用的电机选择了Simulink自带的模块Permanent Magnet Synchronous Machine。模块一共包括四个输入端，分别是A、B、C三相电流的输入端外加一个转矩输入端。当转矩T＞0时为电动状态，反之为发电状态。电机以直流电源通过逆变器产生的三相电作为供电输入，逆变器的触发信号由PWM模块的输出控制信号提供，如图4-3所示。永磁同步电机的参数：额定电压220V、相电阻、电枢电感0.00395H、极对数4、转动惯量J为。

图4-3 永磁同步电机电机模块

                                             图4-4 矢量控制模块结构

                  

图4-5 Subsystem5模块结构

                                            图4-6 解耦模块结构图

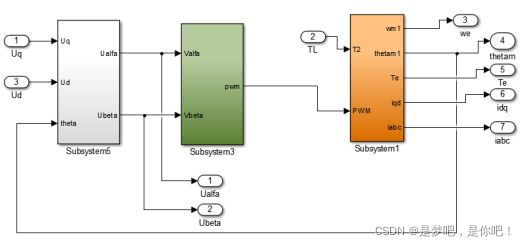
图4-4为矢量控制模块结构，整个矢量控制系统由三个子模块组成，分别是图中的Subsystem5、Subsystem1和Subsystem3。其中Subsystem5模块由mux模块、Fcn模块构成，如图4-5所示。模块是将输入的ud、uq和转矩角通过三相静止坐标系与两相静止坐标系的坐标转换公式得到uα、uβ。Subsystem3模块就是SVPWM模块，其作用是将得到的uα、uβ来通过SVPWM过程产生需要的PWM控制波，用于电动机逆变器的控制。Subsystem3即为电动机模块，如图4-3所示，主要器件包括直流电源、通用桥、永磁同步电机模块以及Fcn模块。直流电源设置为130V。通用桥的参数设置：缓冲电阻、缓冲电容Cs为正、器件选择为IGBT、、。

如图3-6所示是解耦模块的结构图，选择的器件包括：Mux、Fcn。选择的电感和MTPA模块相同。由MTPA模块产生的电流分量参考值id*、iq*和角速度ω经过解耦模块，根据相关公式和设定的参数，就可以得到电压分量ud、uq，用于输入矢量控制模块，最终控制电机。

4.3 仿真结果及分析

4.3.1 仿真波形图

                  

图4-7 转速变换波形图

                                                 图4-8 转矩变换波形图

图4-7为永磁同步电机的转速变换波形图。转速设置的参考值是，最终得到的稳定转速为实现调速要求。转速从零开始增长，在前转速基本成线性增加，增加的速度较快。到达之后，转速的增长速度明显下降，此时转速达到。转速缓慢增长到左右，转速达到最大值并开始减小，最终在左右趋于稳定。

图4-8为永磁同步电机转矩变化波形图。由图可知，调速开始之后，系统的转矩直接提高到，并且转矩在前之内一直保持在最大转矩的转态。一直到时，转矩在短时间内快速降低到左右并一直维持到左右的时间点，之后转矩转为负值，直到左右转矩变为零并保持稳定。

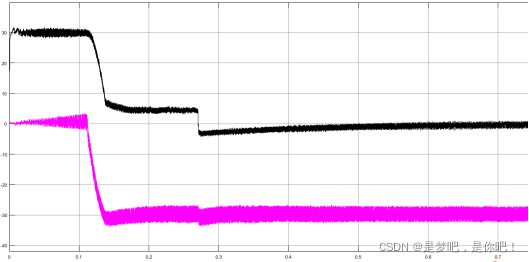
图4-9为永磁同步电机电流分量id、iq变化的波形图，上方的波形为iq的变换过程，下方的波形图为id的变换过程。在之前，电流iq的值一直保持在左右，此时电流id的值保持为。一直到左右，iq电流的值直接降为，id电流负方向增加到左右。在左右电流出现小幅波动，之后基本保持稳定。

                  

图4-9 电流分量id、iq矢量变换波形图

4.3.2 仿真结果分析

由转速波形图可以看出，电机的转速在前0.13s的时间里响应速度很快，速度随着时间成线性规律上升。由图4-5的转矩波形可以看到在前0.13s内转矩一直保持在最大状态，而由图4-6的电流波形可以看见id电流分量为0，电流矢量只由iq电流分量组成。可见此时电机处在恒转矩区,属于MTPA调速策略，根据MTPA轨迹使得转矩一直保持在最大状态，并且转速没有达到指定值，由开关控制保持。在0.13秒左右时电机速度达到基速转为弱磁调速，速度增长明显减慢，由转矩波形可以看出在0.13s左右的节点转矩出现下降。而由电流矢量波形所示，在进入弱磁调速后iq电流矢量下降为，id电流矢量负方向增大。在0.27秒左右电机速度达到最大值并开始下降，最终电机的速度在0.7秒左右趋于稳定，完成整个调速过程，转矩和电流也趋于稳定，没有出现再过大的波动。

整个仿真过程完整的实现了MTPA调速和弱磁调速过程，将电动机转速快速的调节到设定值，并通过弱磁调速实现在基速区以上的稳定调速，增大了调速范围。结果表明搭建的弱磁调速系统仿真模型成功实现了稳定调速的要求。

5 结论 

本文通过对永磁同步电机的控制策略进行分析，规划了d-q坐标系下的MTPA和弱磁控制轨迹，最后基于Simulink建立了永磁同步电机的最大转矩电流比弱磁控制。通过仿真得到的转矩、电流矢量和转速波形可以知道，基于电动机基速区和弱磁Ⅰ区而建立的弱磁系统仿真模型能够实现基速区以上的宽范围调速，并且能够达到较快的响应速度，实现电动机的迅速宽范围调速。在整个调速过程中电机的转速和转矩都能保持平稳，没有出现大幅度的波动，这都说明了所设计的系统具有较好的动态和静态性能。同时，无论电机的恒转矩区基于MPTA轨迹的升速过程还是弱磁调速过程，都和实际的理论分析吻合，从而证明所设计系统的可行性和正确性。

永磁同步电机相较于其他电机具有弱磁调速性能好、控制系统简单等有优点，所以当矢量控制策略被提出后，永磁同步电动机在电动车驱动系统中很快成为了主流。但是永磁同步电机也存在着其本身不可忽视的一些问题，比如永磁体的不可逆退磁和深度弱磁调速带来的振荡等等，这些都是永磁同步电机应用所面对的问题，同时也为电动车用永磁同步电机的调速带来了很多的阻碍，这都是永磁同步电机极需解决的问题，也是永磁同步电机可以持续发展的方向。永磁同步电机的不断发展，不仅能为电动汽车带来新的方向，同时也能为各个领域的电机选择提供更多可能，这会为国家的工业发展带来更大助力。

 参考文献

[1] Jahns T M .Flux-Weakening Regime Operation of an Interior Permanent-Magnet Synchronous Motor Drive[J].IEEE Transactions on Industry Applications,1985, IA-23(4):681-689.

[2] Chen H， Jin J , Chen J , Catching up in New Energy Vehicle Industry: Review of itsDe ve lopment and Policies in China[C]// Management of Innovation and Technology, 2008.ICMIT 2008.4th IEEE International Confeenee on. IEEE, 2008.

[3] 马建,刘晓东，陈轶嵩，等.中国新能源汽车产业与技术发展现状及对策[J].中国公路学报, 2018, 31(08): 1-19. .

[4]胡堋湫，谭泽富，邱刚，王欣煜，邓明.电动汽车发展综述[J]电气应用，2018, 37(20):79- 85.

[5] ChauK T ,ChanC C , Liu C .Overvie w of Permanent-Magnet Brushless D -rives for Eleetric and Hybrid Eleetric Vehicles[J]. IEEE Transactions on Industrial Eleetronics,2008,55(6):2246-2257.

[6]温传新，王培欣，花为.电动汽车驱动系统的研究现状与发展趋势[J].微电机, 2019,52(10): 103-109. .

[7] Widmer J D，Martin R , Kimiabeigi M . Electric Vehicle Traction Motors Without RaeEarth M agnets[J] slstainable Materials and Technologies, 2015, 3: 7-13.

[8] Zhai L ,Sun T , Wang J . Electonic stability Contuol Based on Motor Driving and Braking Torque Distnibution for a Four In-Wheel Motor Drive Electric Vehic -le[J]. IEEE Transac tionson Vehicular Technology, 2016, 65(6): 4726 4739. .

[9] Husin Z A , Sulaiman E , Khan F , et al. Design Studies and Effect of Various Rotor Pole Number of Field Excitation Flux Switching Motor for Hybrid Electric Vchicle Applications[C]// 2014 IEEE 8th International Power Engineering and Opti mization Conference(PEOCO2014), Langkawi, 2014, pp.144- 149.

[10] Uzhegov N , Kurvinen E . Nerg J ,ct al. Mutidiseiplinary Design Process of a 6-Slot 2-PoleHigh-S peed Permanent Magnet Synchronous Machine[J].IEEE Transactions on Industrial on Industrial Electronics,2016,63(2):784-795.

[11]彭海涛，何志伟，余海阔.电动汽车用永磁同步电机的发展分析[J].微电机，2010,43(06): 83-86.