李宏毅 2020机器学习作业1 详细解析

课程链接：http://speech.ee.ntu.edu.tw/~tlkagk/courses_ML20.html
要做这个作业的话需要一定的高数、线代的基础，而且尽量要会使用python的numpy模块。这篇文章大体还是按着baseline走的。

必要的前提条件

1.记得要把numpy、pandas、csv模块给安装好（网上有很多教程,找适用于你的开发环境的就好）。
2.学习一下numpy的使用：gitbook，直接看第四章即可
3.先去Kaggle把需要的数据下载好（点我跳转到kaggle）：

test.csv和train.csv都下载下来。这两个分别是测试和训练需要用到的数据（表格的形式呈现）。

1.分析问题

训练数据

给出空气品质监测网所一年每个月20天的观测记录，其中观测量有18个（AMB_TEMP, CH4, CO,PM2.5…）。每天每个小时测量一次所有观测量。

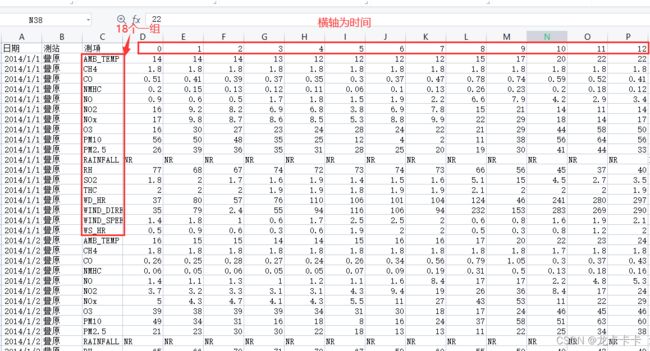
在train.csv中，观测量每18个为一组，表示一天的所有观测量。横轴表示的是一天内的时间点。

测试数据

测试数据中，给出了连续的9个小时的测量数据，我们需要根据这9个小时的测量数据来预测第10个小时的PM2.5的值。

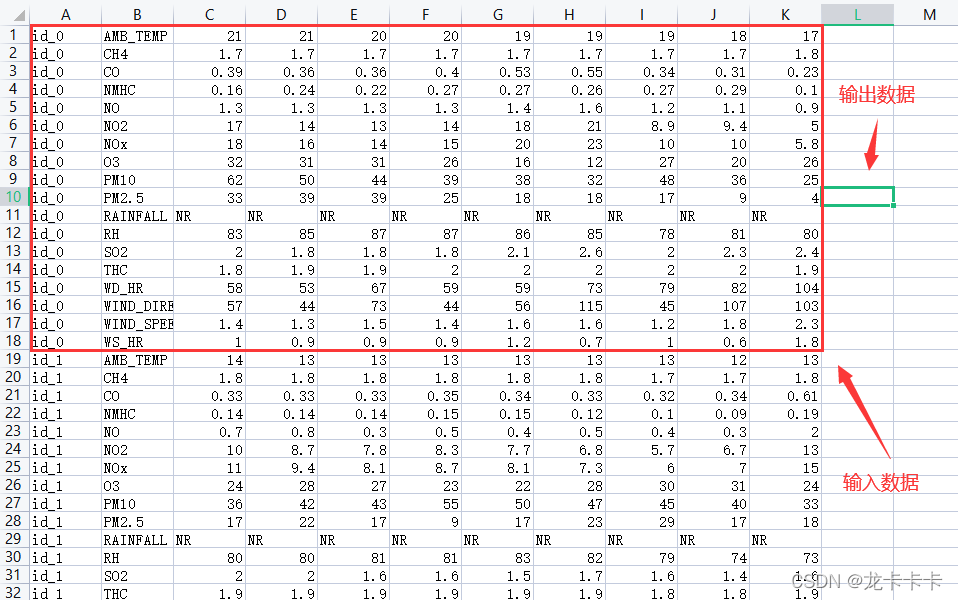
看上图可知，我们需要训练的Model的input应该是这18个测量数据在9个小时内的所有测量值，而output则是第10个小时的PM2.5的值。

2.数据的预处理

读入train.csv到内存中并简单处理

使用pandas读入数据，iloc的功能是将数据切片。
RAINFALL栏的值中出现了 ‘NR’ 字符（not rain：没有下雨），这个值我们是需要转换为整数值来处理的。由于没有下雨，所以将其值设为0（降雨量为0）即可。

import pandas as pd
import numpy as np
import csv
import math

#读取csv文件
#记得将下载的数据放到与该py文件相同的目录下
data = pd.read_csv('./train.csv', encoding = 'big5')#繁体中文->big5编码
#截取数据部分（去掉日期、測站、測項）
data=data.iloc[:,3:]#截取所有行（第一行是header，read_csv时不会放入data中），第3列以后的所有列
#将所有NR替换为0
data[data=='NR']=0  #这里的用法与numpy中的布尔型索引一样
# 从DataFrame转为ndarray
raw_data=data.to_numpy() #将数据转为numpy可处理的类型，以便后续使用Numpy模块处理

Extract Features（1）（提取特征）

由于每个月的数据是连续20天的，所以这20天的数据可以拼接起来使用。如上图，将每个月的数据拼接成一个长条状（不区分天数，我们只关心连续的10小时的数据）。

#将数据根据月份分组
month_data={}
for month in range(12):
    #将每个月20天的数据拼接起来
    linked=np.empty((18,480))
    for day in range(20):
        linked[:,day*24:(day+1)*24]=raw_data[month*20*18+day*18:month*20*18+(day+1)*18,:]
    month_data[month]=linked

Extract Features (2)

得到了每个月连续的480个小时的数据以后，我们要将这些数据转换为Function预测时的输入和输出。
刚刚说了，input就是连续9个小时的18个测量量的值，output是第10个小时的PM2.5的值。所以，可以将每个月连续的480个小时的数据进行切分。每次切10个小时的数据，然后对特征进行扁平化处理（即将特征矩阵转化为特征向量）（每个测量量每个小时的值作为一个特征，一共18*9个特征）。一个月一共480个小时，可提取471组数据。

#将数据整合为x和y的映射，对特征矩阵进行扁平化处理
x=np.empty((12*471,18*9))   #x[i][j] i号数据的第j个特征值
y=np.empty((12*471,1))

for month in range(12):
    for hour in range(471):#每月的471个数据
        x[month*471+hour]=month_data[month][:,hour:hour+9].reshape(1,-1)
        #[:,hour:hour+9]每次取9个小时的数据
        #reshape将矩阵扁平化为行向量
        y[month*471+hour]=month_data[month][9,hour+9]

Normalize 归一化

归一化，即对每个特征，求其均值和标准差。然后将每个数值都减去其均值后再除以标准差，这样特征的期望就变成了0，标准差变成1。至于为什么要标准化，参考：https://blog.csdn.net/weixin_42080490/article/details/108891002。

#对特征做Normalization
mean_x=np.mean(x,axis=0) #axis=0对列求均值，返回一个行向量（每个特征的均值）
std_x=np.std(x,axis=0) #axis=0对列求标准差，返回一个行向量（每个特征的标准差）

for i in range(18*9):
    if std_x[i] !=0:
        x[:,i]=(x[:,i]-mean_x[i])/std_x[i]

3.将数据分为训练集和验证集

如果需要对模型进行对比的话，需要做这个操作。

#将训练集划分为训练集和验证集,共分total组，取第i组作为验证集
def reArrangeTrainValidation(x,i=0,total=5):
    group_size = int(len(x) / total)  # 分total组
    x_train=np.concatenate((x[:group_size*i],x[group_size*(i+1):]),axis=0)
    y_train=np.concatenate((y[:group_size*i],y[group_size*(i+1):]),axis=0)
    x_validation=x[group_size*i:group_size*(i+1)]
    y_validation=y[group_size*i:group_size*(i+1)]
    return (x_train,y_train),(x_validation,y_validation)

4.Model的选择

Baseline中的model选择的是简单的一次函数，如果想要优化的话我们需要考虑次幂更高的函数。下面在GradientDescent的环节中采用的就是n次函数。

5.LossFunction

baseline中输出的时候采用的是 Root Mean Square Error（均方根误差），但是GradientDescent的时候还是使用的残差平方和来计算梯度。
至于梯度的计算过程以后再补上。

6.GradientDescent算法

采用Adagrad优化算法，不要觉得这个算法没见过就不想学了，其实该算法编写很简单，理解也不难 。该算法主要思想是根据⾃变量在每个维度的梯度值的⼤小来调整各个维度上的学习率，从⽽而避免统一的学习率难以适应所有（参数）维度的问题。
该部分主要难点在于矩阵的运算，想要理解的话还需要熟悉Loss函数及其偏导，对数学能力有一定要求。

def computeY(n,x,w):#根据权重和输入计算输出
    py = np.zeros([len(x), 1])
    for e in range(1 + n):#e为当前x的次幂。e=0表示常数项，这里常数项并没有合并为一个，而是一个特征一个常数项。
        py += np.dot(x ** e, w[e])#w[e]表示ax^e中的系数a构成的向量
    return py

def gradientDescent(n,x,y):#n:采用n次函数
    dim = 18 * 9
    # 采用adagrad算法
    w = [np.zeros([dim, 1]) for e in range(1 + n)]	#权重。就是每个特征变量前面的系数
    adagrad = [np.zeros([dim, 1]) for e in range(1 + n)]  # adagrad中的梯度累计变量
    learning_rate = 100
    iter_time = 10001
    eps = 0.0000000001  #用于避免除0错误
    for t in range(iter_time):
        py=computeY(n,x,w)
        loss = np.sqrt(np.sum(np.power(py - y, 2)) / len(x))
        if (t % 100 == 0):
            print(str(t) + ":" + str(loss))
        for e in range(1 + n):
            gradient = 2 * np.dot(x.transpose() ** e, py - y)#理解该过程的计算需先看懂上面矩阵运算那张图
            adagrad[e] += gradient ** 2	#统计梯度平方
            w[e] = w[e] - learning_rate / np.sqrt(adagrad[e] + eps) * gradient	#梯度下降
    for e in range(1+n):
        np.save(str(e)+'.weight.npy', w[e])

7.测试数据处理

对测试数据做与训练数据相同的处理

#载入testing data，对其做相同的处理
testdata=pd.read_csv('./test.csv',header = None,encoding='big5')#header=None说明没有头部，不写的话第一行不会读取到数据中
test_data=testdata.iloc[:,2:]
test_data[test_data=='NR']=0
test_data=test_data.to_numpy()
test_x=np.empty([240,18*9],dtype=float)
for i in range(240):
    test_x[i]=test_data[i*18:(i+1)*18,:].reshape(1,-1)

for i in range(18*9):
    if std_x[i] !=0:
        test_x[:,i]=(test_x[:,i]-mean_x[i])/std_x[i]

8.对testing data做预测

刚刚已经把训练过的权重保存在了文件中，现在将其从文件中读取出来:

#载入权重
w=[]
for e in range(1+n):
    w.append(np.load(str(e)+'.weight.npy'))

然后进行预测的计算:

py=computeY(n,test_x,w)

到这里基本已经结束了，剩下的就是将结果写入到文件中，然后我们就可以提交到kaggle上面看看分数如何了。

9.Save Prediction to CSV File(将预测结果保存至csv文件中)

with open('submit.csv', mode='w', newline='') as submit_file:
    csv_writer = csv.writer(submit_file)
    header = ['id', 'value']
    print(header)
    csv_writer.writerow(header)
    for i in range(240):
        row = ['id_' + str(i), py[i][0]]
        csv_writer.writerow(row)
        print(row)

10.将结果上传到kaggle做评测

在这里提交你的结果：https://www.kaggle.com/competitions/ml2020spring-hw1/submit


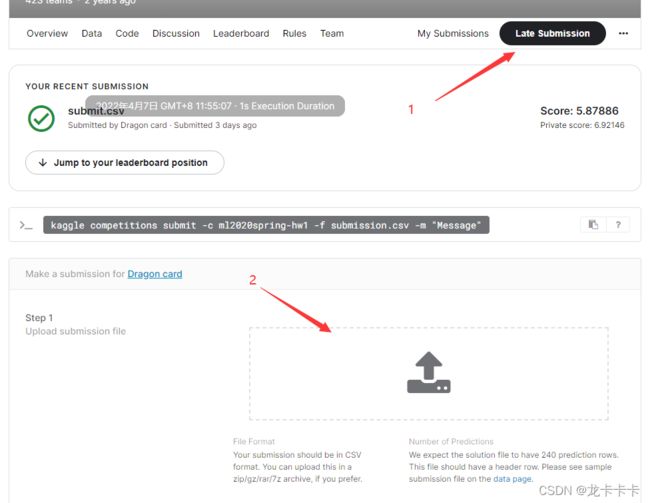
然后就可以看到我们的分数啦：

分数（误差）越低越好。如果分数不理想，那么可以通过调整GradientDescent时候的leaning_rate（学习率）和iter_time（迭代次数）来进一步优化。还可以尝试不同的Model（不同的次幂）。

模型的择优（验证集的使用）

利用该函数，可以查看模型在训练集和验证集上的Error。

def gradientDescentWithValidation(n,x_train, y_train, x_validation, y_validation):#n次幂函数的梯度下降
    dim=18*9 #每个次幂的维度
    # 采用adagrad算法
    w = [np.zeros([dim, 1]) for e in range(1+n)]
    adagrad=[np.zeros([dim,1]) for e in range(1+n)]# adagrad中的梯度累计变量
    learning_rate = 100
    iter_time = 5001
    eps = 0.0000000001
    for t in range(iter_time):
        py_train=np.zeros([len(x_train),1])
        py_validation=np.zeros([len(x_validation),1])
        for e in range(1+n):
            py_train+=np.dot(x_train**e,w[e])
            py_validation+=np.dot(x_validation**e,w[e])
        loss=np.sqrt(np.sum(np.power(py_train-y_train,2))/len(x_train))
        error=np.sqrt(np.sum(np.power(py_validation-y_validation,2))/len(x_validation))
        if (t % 100 == 0):
            print(str(t) + ":" + str(loss) + "," + str(error))
        for e in range(1+n):
            gradient=2*np.dot(x_train.transpose()**e,py_train-y_train)
            adagrad[e]+=gradient**2
            w[e] = w[e] - learning_rate / np.sqrt(adagrad[e] + eps) * gradient