A星(A*、A Star)路径规划算法详解(附MATLAB代码)
首先看看运行效果,分别有三种模式,代码运行前需要通过鼠标点击设置起点和终点。
第一种模式直接输出最短路径
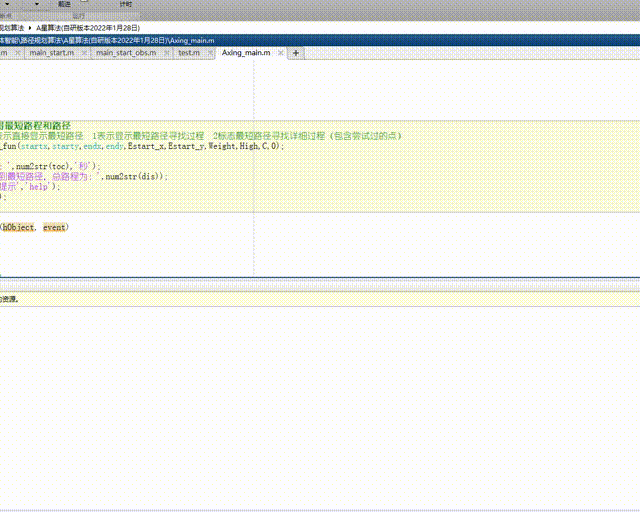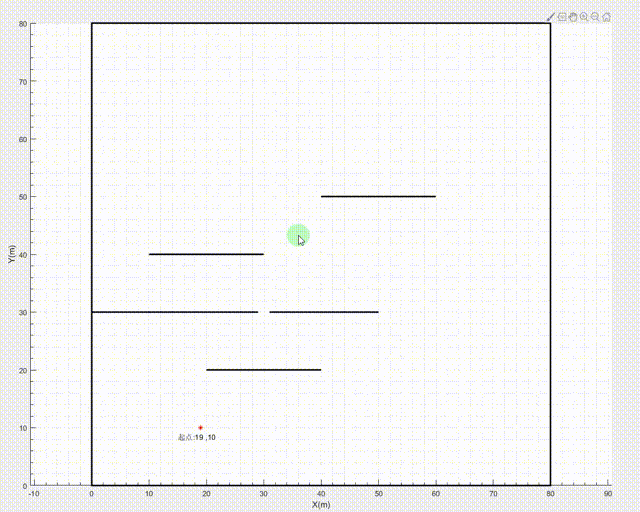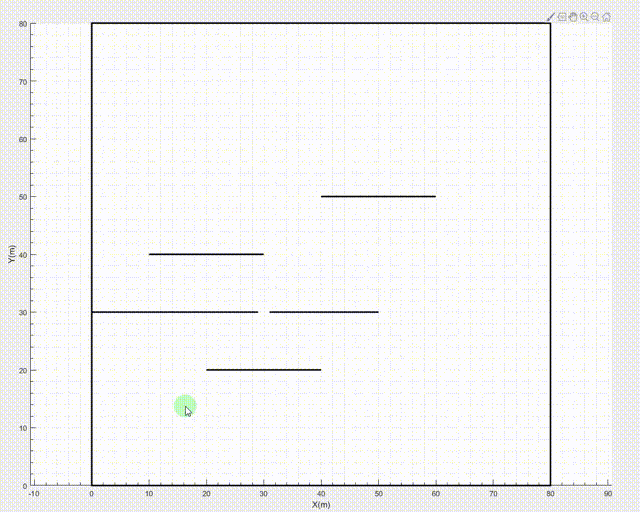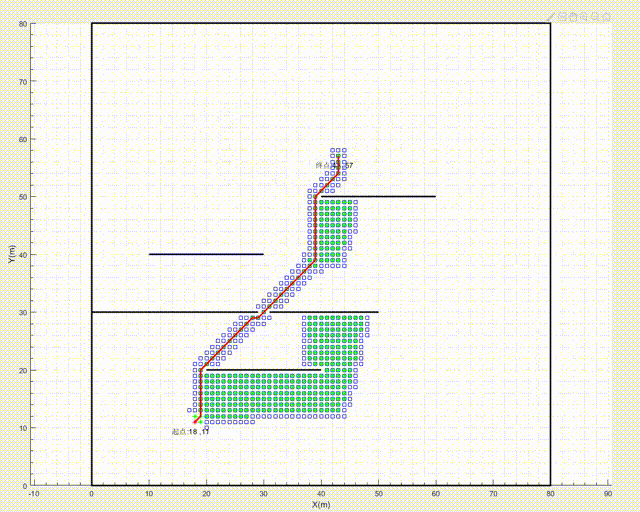
第二种模式输出最短路径的生成过程
第三种模式输出最短路径的生成过程和详细探索的过程
一、A* 算法原理
二、A* 算法实现步骤
三、A* 算法MATLAB代码
某站上我也发了视频,不过之前的版本没有添加鼠标点击功能,这里不能粘贴某站的链接,会被视为打广告,某站搜索“晨少的bili”,即可在主页上看到
一、A* 算法原理
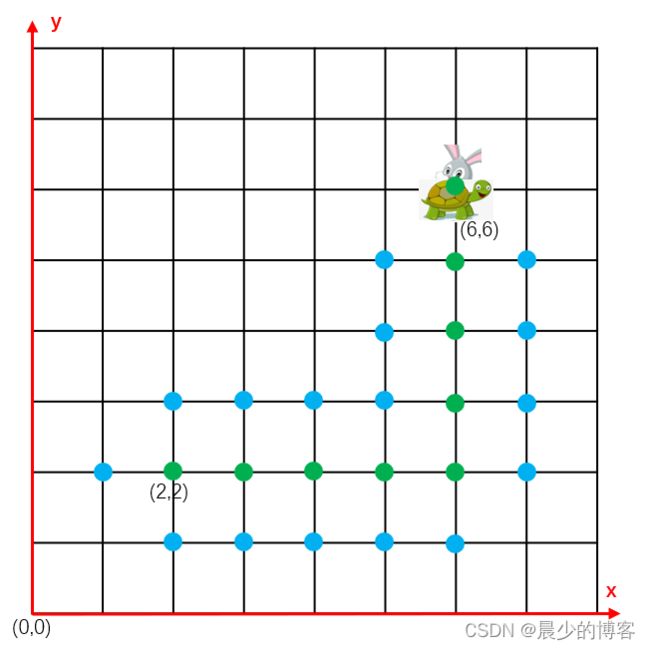
举个例子来说,A*算法通常要将地图网格化,如下图所示:
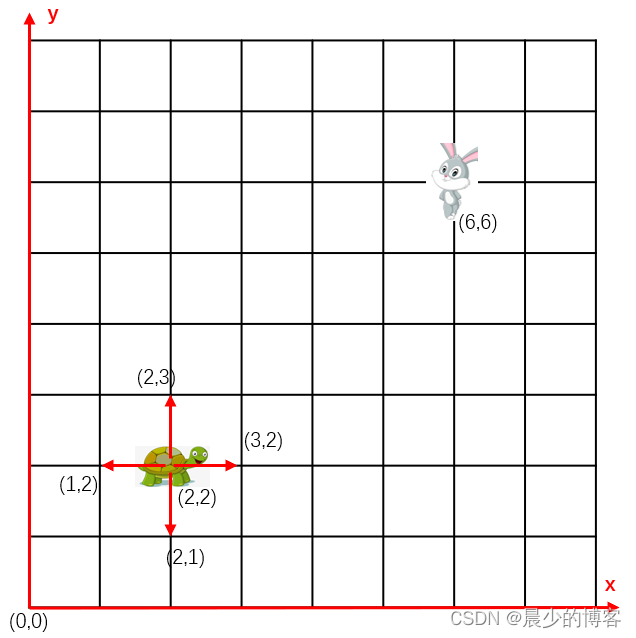
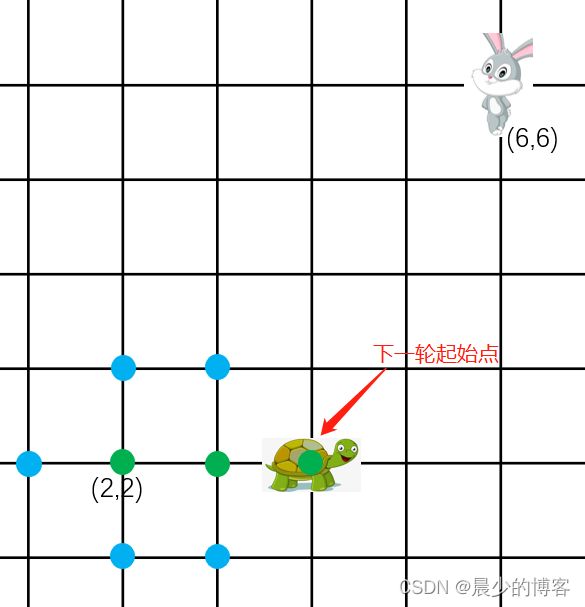
假设有一只乌龟在追小白兔,乌龟此时的位置是(2,2),小白兔的位置是(6,6),假设小白兔静止不动。
根据A *算法的原理,乌龟只能向左、向右、向上、向下走,那么(1,2)、(2,1)、(3,2)、(2,3)是乌龟下一轮可以到达的点,这些点叫做 待探索的点
步骤一
寻找下一步可以到达的节点,将这些待探索的点加入待探索数组 frontier 中,也叫边界数组。
计算出新加入点的代价,代价 = 当前代价 + 预估代价 , 公式表达为 F= G + H
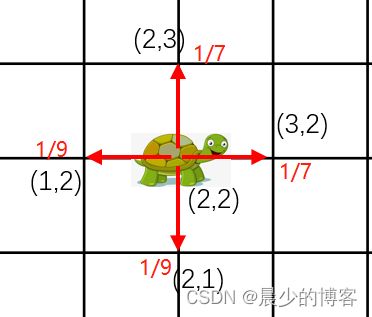
所谓 当前代价 G 就是从起点到达当前点所经过的路程,例如(1,2)、(2,1)、(3,2)、(2,3)这四个点的当前代价都等于(2,2)点到达其所需的路程,即为 1 。
所谓 预估代价 H 就是从当前点到终点的曼哈顿距离(横纵坐标差值之和,| x1 - x2| + |y1 - y2|)
所以(1,2)、(2,1)、(3,2)、(2,3)四个待探索点的预估代价分别为9、9、7、7 。
当前代价 / 预估代价结果如下图所示:
步骤二
将待探索点按照代价的大小升序排序,则排序后的待探索数组中待探索点的顺序为
(3,2)、(2,3)、(1,2)、(2,1)
接着取出第一个,即代价最小的点作为小乌龟的此轮目标点,即为下一轮的起始点,并把该点从待探索数组 frontier 中删去 ,加入 已探索数组 already_frontier 中,则会得到下面的情况:
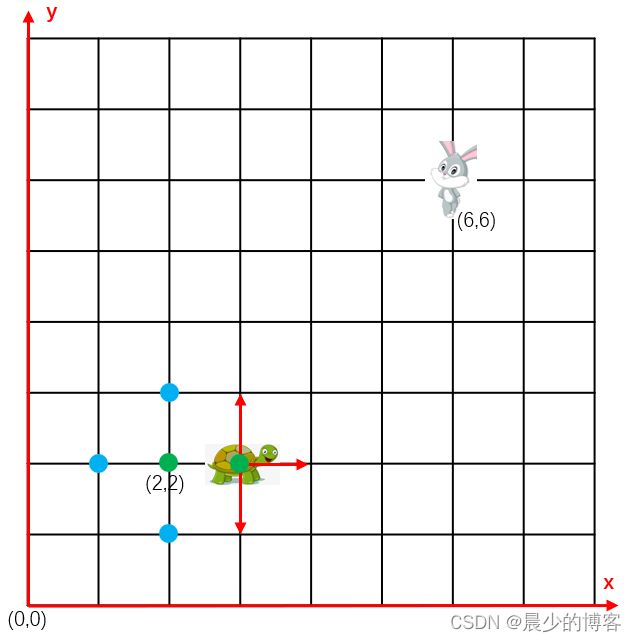
此时小乌龟在(3,2)位置,且为了更形象的表达,图中将待探索点标成了蓝色,已探索点标成了绿色(已探索点目前有(2,2)和(3,2),待探索点有(1,2)、(2,1)、(2,3))
步骤三
记录下当前点到起点的路径,可以这么记 [(2,2) , (3,2)],在matlab中可以表现为一个2行2列的矩阵
2 2
3 2
接着判断当前节点是否是终点,如果不是终点则继续步骤一,继续寻找下一步可以探索的点
为了便于大家的理解,再跟着步骤一、二、三进行下一轮
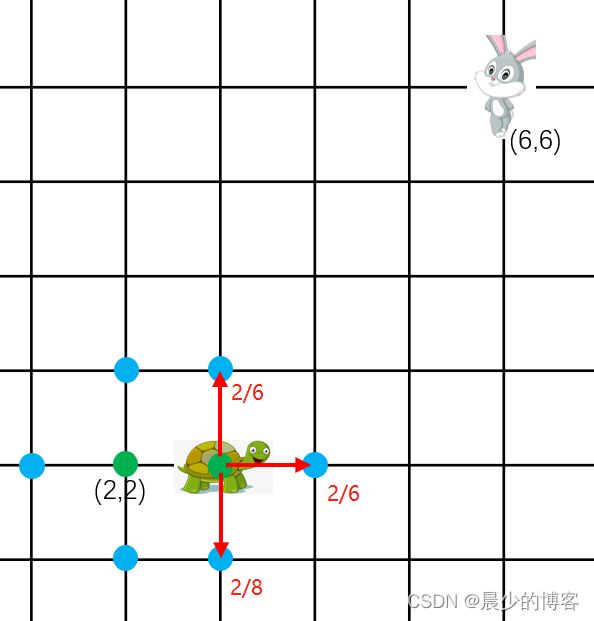
如上图所示,找出小乌龟下一轮可以去到的点,判断周围的点是否在已探索数组 already_frontier 中,如果在则忽略,接着判断这些点是否已经在待探索数组 frontier 中,如果在则比较该点的 当前代价G 与 如果经过小乌龟当前位置而到达该点现在位置所需的 当前代价G2 进行比较,如果G > G2则将该点的上一个节点(可以理解为父节点)改成小乌龟当前所在节点,更新其当前代价为G2。
最后计算出他们的代价,接着对待探索数组升序排序后,选出第一个代价最小的点作为下一轮的起始点。
由于我是以 左下右上 的顺序寻找待探索点的,所以前两次选择到的代价最小是(3,2)和(4,2),如果你按照 上右下左的顺序,则你选择到的代价最小会是(2,3)和(2,4),这个并不会影响到最终的最短路径长度,只是路径不同罢了
根据上面三个步骤一直循环,就可以得到一条最短的路径,下图绿色点表示的即为最短路径
当然也可以是先往上走,再往右走,根据每个人自己选择的待探索点的顺序来确定
二、A* 算法实现步骤
- 将起点加入待探索数组 frontier ,代价赋为 0
- 找出 frontier 中代价 F 最小的点,移出 frontier ,添加进已探索数组 already_frontier
- 判断该点是否是终点,如果不是则继续
- 将该节点周围的四个点找出,判断这四个点是否在 already_frontier数组中,如果在则忽略(当然这四个点也不能超出地图范围或者位于障碍物中)。
- 判断这些点是否已经在待探索数组 frontier 中,如果在,则将该点的 当前代价G 与 经过当前节点到达该点的 当前代价G2 进行,如果G > G2则将该点的上一个节点(可以理解为父节点)改成当前节点,更新其当前代价为G2,并更新其 代价F。(这一步非常重要,有利于找出更加短的路径)
- 将剩下符合要求的点添加进 frontier ,并计算 代价 F,对 frontier 数组按照 代价 F 排序
- 同时记录下路径,即每个节点都要记录其上一个节点,方便最后进行路径的回溯找出最短路径
- 循环 2 - 7 步骤,直到到达终点终止循环
补充:对于第四步来说,可以将可运动方向改为八个方向,即上、下、左、右、左上、左下、右上、右下,需要注意的是每次运动的步长就不只是 1 了,还有根号 2 ,我写的A*算法仿真(文章开头的那个演示)就是按照八个方向来写的,这样得出的路径会更贴合实际。
三、A* 算法MATLAB代码
代码是2022年除夕前一天完成的,博主写代码不易,还请各位大佬支持一下,哈哈
xian鱼APP里搜索用户 “晨少的咸鱼” ,主页里有你们想要的东西哦