A*算法详解一看就懂（python）

定义

A*算法，A*（A-Star)算法是一种静态路网中求解最短路径最有效的直接搜索方法，也是解决许多搜索问题的有效算法。算法中的距离估算值与实际值越接近，最终搜索速度越快。

定义解析

• A*算法是一个“搜索算法”，实质上是广度优先搜索算法（BFS）的优化。从起点开始，首先遍历起点周围邻近的点，然后再遍历已经遍历过的点邻近的点，逐步的向外扩散，直到找到终点。
• A*算法的作用是“求解最短路径”，如在一张有障碍物的图上移动到目标点，以及八数码问题（从一个状态到另一个状态的最短途径）
• A*算法的思路类似图的Dijkstra算法，采用贪心的策略，即“若A到C的最短路径经过B，则A到B的那一段必须取最短”，找出起点到每个可能到达的点的最短路径并记录。
• A*算法与Dijkstra算法的不同之处在于，A*算法是一个“启发式”算法，它已经有了一些我们告诉它的先验知识，如“朝着终点的方向走更可能走到”。它不仅关注已走过的路径，还会对未走过的点或状态进行预测。因此A*算法相交与Dijkstra而言调整了进行BFS的顺序，少搜索了哪些“不太可能经过的点”，更快地找到目标点的最短路径。另外一点，由于H选取的不同，A*算法找到的路径可能并不是最短的，但是牺牲准确率带来的是效率的提升。

例子问题描述

举两个有代表性的例子，以便读者更形象化地理解A*算法

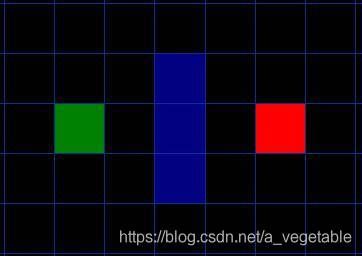
最短路径

中间蓝色是障碍物，求从绿色到红色的最短路径

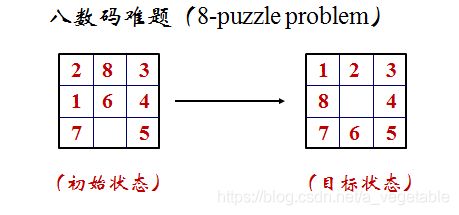
八数码

在九宫格里放在1到8共8个数字还有一个是空格，与空格相邻的数字可以移动到空格的位置，问给定的状态最少需要几步能到达目标状态（用0表示空格）：
 

关键内容——启发函数

计算出组成路径的方格的关键是下面这个等式（启发函数）：

这里，

G = 从起点 A 移动到指定方格的移动代价，沿着到达该方格而生成的路径。

H = 从指定的方格移动到终点 B 的估算成本。这个通常被称为试探法，有点让人混淆。为什么这么叫呢，因为这是个猜测。直到我们找到了路径我们才会知道真正的距离，因为途中有各种各样的东西 ( 比如墙壁，水等 ) 。

G来源于已知点信息，H来源于对未知点信息的估计，F为选择下一个将遍历节点的依据。

此外，H还有一个特征：

• 在极端情况下，当启发函数h(n)始终为0，则将由g(n)决定节点的优先级，此时算法就退化成了Dijkstra算法。
• 如果h(n)始终小于等于节点n到终点的代价，则A*算法保证一定能够找到最短路径。但是当h(n)的值越小，算法将遍历越多的节点，也就导致算法越慢。
• 如果h(n)完全等于节点n到终点的代价，则A*算法将找到最佳路径，并且速度很快。可惜的是，并非所有场景下都能做到这一点。因为在没有达到终点之前，我们很难确切算出距离终点还有多远。
• 如果h(n)的值比节点n到终点的代价要大，则A*算法不能保证找到最短路径，不过此时会很快。
• 在另外一个极端情况下，如果h()n相较于g(n)大很多，则此时只有h(n)产生效果，这也就变成了最佳优先搜索。

由上面这些信息我们可以知道，通过调节启发函数我们可以控制算法的速度和精确度。因为在一些情况，我们可能未必需要最短路径，而是希望能够尽快找到一个路径即可。这也是A*算法比较灵活的地方。

对于网格形式的图，有以下这些启发函数可以使用：

• 如果图形中只允许朝上下左右四个方向移动，则可以使用曼哈顿距离（Manhattan distance）。计算从当前万格横可或纵回移动到达目标所经过的方格数。
• 如果图形中允许朝八个方向移动，则可以使用对角距离。横纵移动和对角移动都是合法的。为提高效率，常取整数作系数10，14.
• 如果图形中允许朝任何方向移动，则可以使用欧几里得距离（Euclidean distance）。两点直线距离。

GitHub代码

https://github.com/while-TuRe/A-star-ShortestPath（用vscode即可运行）

算法思路

开始搜索(Starting the Search)

一旦我们把搜寻区域简化为一组可以量化的节点后，就像上面做的一样，我们下一步要做的便是查找最短路径。在 A* 中，我们从起点开始，检查其相邻的方格，然后向四周扩展，直至找到目标。

我们这样开始我们的寻路旅途：

1. 从起点 A 开始，并把它就加入到一个由方格组成的 open list( 开放列表 ) 中。这个 open list 有点像是一个购物单。当然现在 open list 里只有一项，它就是起点 A ，后面会慢慢加入更多的项。 Open list 里的格子都是下一步可以到达的（当然可能是退回某点后下一步到达），在最终最短路径中，open list中的格子可能会是沿途经过的，也有可能不经过。基本上 open list 是一个待检查的方格列表。

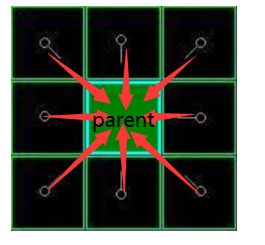
2. 查看与起点 A 相邻的方格 ( 忽略其中墙壁所占领的方格，河流所占领的方格及其他非法地形占领的方格 ) ，把其中可走的 (walkable) 或可到达的 (reachable) 方格也加入到 open list 中。把起点 A 设置为这些方格的父亲 (parent node 或 parent square) 。当我们在追踪路径时，这些父节点的内容是很重要的。因为它记录了从起点到该点的最短路径上经过的最后一个节点。

3. 把 A 从 open list 中移除，加入到 close list( 封闭列表 ) 中， close list 中的每个方格都是现在不需要再关注的。

4. 下一步，我们需要从 open list 中选一个方格，重复23步骤。但是到底选择哪个方格好呢？具有最小 F 值的那个。

所以，我们的路径是这么产生的：反复遍历 open list ，选择 F 值最小的方格，产生新的可供选择的方格，直到找到终点方格。这个过程稍后在“继续搜索”详细描述。我们还是先看看怎么去计算上面的等式。

计算启发函数

如上所述， G 是从起点Ａ移动到指定方格的移动代价。H是从指定方格移动到终点的估计代价。

G的计算思路类似图的Dijkstra算法，采用贪心的策略，即“若A到C的最短路径经过B，则A到B的那一段必须取最短”，找出起点到每个可能到达的点的最短路径并记录。既然我们是沿着到达指定方格的路径来计算 G 值，那么计算出该方格的 G 值的方法就是找出其父亲的 G 值，然后按父亲是直线方向还是斜线方向加上 10 或 14 。在本例中，横向和纵向的移动代价为 10 ，对角线的移动代价为 14 。之所以使用这些数据，是因为实际的对角移动距离是 2 的平方根，或者是近似的 1.414 倍的横向或纵向移动代价。使用 10 和 14 就是为了简单起见。比例是对的，我们避免了开放和小数的计算。这并不是我们没有这个能力或是不喜欢数学。使用这些数字也可以使计算机更快。稍后你便会发现，如果不使用这些技巧，寻路算法将很慢。

有很多方法可以估算 H 值。这里我们使用 Manhattan 方法，计算从当前方格横向或纵向移动到达目标所经过的方格数，忽略对角移动，然后把总数乘以 10 。之所以叫做 Manhattan 方法，是因为这很像统计从一个地点到另一个地点所穿过的街区数，而你不能斜向穿过街区。重要的是，计算 H 是，要忽略路径中的障碍物。这是对剩余距离的估算值，而不是实际值，因此才称为试探法。

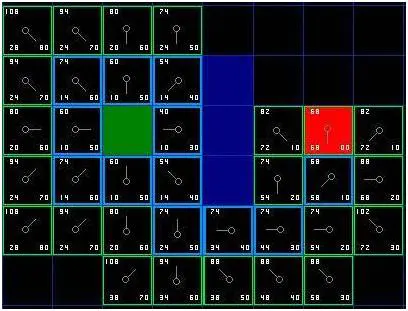
把 G 和 H 相加便得到 F 。我们第一步的结果如下图所示。每个方格都标上了 F ， G ， H 的值，就像起点右边的方格那样，左上角是 F ，左下角是 G ，右下角是 H 。

继续搜索(Continuing the Search)

为了继续搜索，我们从 open list 中选择 F 值最小的 ( 方格 ) 节点，然后对所选择的方格作如下操作：

1.       把它从 open list 里取出，放到 close list 中。

2.       检查所有与它相邻的方格，忽略其中在 close list 中或是不可走 (unwalkable) 的方格 ( 比如墙，水，或是其他非法地形 ) ，如果方格不在open lsit 中，则把它们加入到 open list 中。

把我们选定的方格设置为这些新加入的方格的父亲。

3.       如果某个相邻的方格已经在 open list 中，则检查这条路径是否更优，也就是说经由当前方格 ( 我们选中的方格 ) 到达那个方格是否具有更小的 G 值。如果没有，不做任何操作。

 以下是代码的关键部分，简化细节便于读者理解。完整代码在GitHub上可供下载参考，用vscode即可运行。如果对您有用请点个赞吧~

https://github.com/while-TuRe/A-star-ShortestPath

def SearchPath(mapp,cp,target_position):
    start_time=time.time()#计时
    board = Board(mapp,target_position)#地图棋盘对象
    board.GetMsg(cp).IsUnk = 0
    open_list.append(cp)
    while(open_list != []):
        #取出第一个（F最小，判定最优）位置
        current_position=open_list[0]
        open_list.remove(current_position)
        #close_list.append(current_position)用mapx中存储的IsUnk（是否unknow）代替，否则需要在close_list中搜索
        #到达
        if(current_position == target_position):
            print("成功找到解")
            按要求输出解
            return

        #将下一步可到达的位置加入open_list，并检查记录的最短路径G是否需要更新，记录最短路径经过的上一个点
        #斜（上下左右与此思路相同，只是细节有差）
        for i in [current_position.x-1,current_position.x+1]:
            for j in [current_position.y-1,current_position.y+1]:
                if(IsInBoard(i,j)):
                    new_G=board.GetMsg(current_position).G+14
                    #维护当前已知最短G,如果未遍历或需更新
                    if(board.mapx[i][j].IsUnk): 
                        board.mapx[i][j].IsUnk=0
                        open_list.append(Position(i,j))
                        board.mapx[i][j].parent=current_position
                        board.mapx[i][j].G=new_G
                        
                    if(board.mapx[i][j].G>new_G):
                        board.mapx[i][j].parent=current_position
                        board.mapx[i][j].G=new_G
        
        #对open_list里的内容按F的大小排序
        open_list.sort(key=lambda elem : board.GetMsg(elem).GetF())

 八数码问题

while-TuRe/A-star-8-Puzzel-Problem: A*八数码问题 (github.com)

八数码问题与最短路径搜索问题的不同主要在于以下几点：

• 目标状态可能无法到达（将棋盘展开按照逆序数的奇偶性进行判断。空格左右移逆序数不变，上下移逆序数变化2）
• close_list不可被替换，open_list中存储的是棋盘的状态（一个3*3的list）
• G表示已走过的步数，H表示每个数字棋子当前位置与目标位置曼哈顿距离的和。

如果您觉得有用，请点亮小心心♥吧~码字不易，多谢鼓励~