理论加实践，终于把时间序列预测ARIMA模型讲明白了

上篇我们一起学习了一些关于时间序列预测的知识。而本文将通过一段时间内电力负荷波动的数据集来实战演示完整的ARIMA模型的建模及参数选择过程，其中包括数据准备、随机性、稳定性检验。本文旨在实践中学习，在实战过程中穿插理论知识梳理和学习，相信大家一定有所收获。

本文主要内容

时间序列建模基本步骤

1. 获取被观测系统时间序列数据。

2. 对数据绘图，观测是否为平稳时间序列；对于非平稳时间序列要先进行  阶差分运算，化为平稳时间序列。

3. 经过第二步处理，已经得到平稳时间序列。要对平稳时间序列分别求得其自相关系数ACF 和偏自相关系数PACF ，通过对自相关图和偏自相关图的分析，得到最佳的阶层  和阶数 。

4. 由以上得到的 、、，得到ARIMA模型。然后开始对得到的模型进行模型检验。

ARIMA模型介绍

ARIMA 模型^[1]是一种流行且广泛使用的时间序列预测统计方法。

ARIMA 是代表autoRegressive I integrated Moving a average^[2]自回归综合移动平均线的首字母缩写词，它是一类在时间序列数据中捕获一组不同标准时间结构的模型。预测方程中平稳序列的滞后称为“自回归”项，预测误差的滞后称为“移动平均”项，需要差分才能使其平稳的时间序列被称为平稳序列的“综合”版本。随机游走和随机趋势模型、自回归模型和指数平滑模型都是 ARIMA 模型的特例。

ARIMA 模型可以被视为一个“过滤器”，它试图将信号与噪声分开，然后将信号外推到未来以获得预测。ARIMA模型特别适合于拟合显示非平稳性的数据。

一般概念

为了能够使用ARIMA，你需要了解一些概念。

平稳性

从统计学的角度来看，平稳性是指数据的分布在时间上平移时不发生变化。因此，非平稳数据显示了由于趋势而产生的波动，必须对其进行转换才能进行分析。例如，季节性会导致数据的波动，并可以通过“季节性差异”过程消除。

差分

从统计学的角度来看，数据差分是指将非平稳数据转换为平稳的过程，去除其非恒定的趋势。“差分消除了时间序列水平的变化，消除了趋势和季节性，从而稳定了时间序列的平均值。”  季节性差分应用于季节性时间序列以去除季节性成分。

ARIMA模型拆解

剖析ARIMA的各个部分，以便更好地理解它如何帮助我们时间序列建模，并对其进行预测。

AR - 自回归

自回归模型，顾名思义，就是及时地“回顾”过去，分析数据中先前的值，并对它们做出假设。这些先前的值称为“滞后”。一个例子是显示每月铅笔销售的数据。每个月的销售总额将被认为是数据集中的一个“进化变量”。这个模型是作为“利益的演化变量根据其自身的滞后值(即先验值)进行回归”而建立的。

I - 表示综合

与类似的“ARMA”模型相反，ARIMA中的“I”指的是它的综合方面。当应用差分步骤时，数据是“综合”的，以消除非平稳性。表示原始观测值的差异，以允许时间序列变得平稳，即数据值被数据值和以前的值之间的差异替换。

MA - 移动平均线

该模型的移动平均方面，是将观测值与应用于滞后观测值的移动平均模型的残差之间的相关性合并。

ARIMA用于使模型尽可能地符合时间序列数据的特殊形式。

ARIMA模型建立

一般步骤

① 首先需要对观测值序列进行平稳性检测，如果不平稳，则对其进行差分运算直到差分后的数据平稳；
② 在数据平稳后则对其进行白噪声检验，白噪声是指零均值常方差的随机平稳序列；
③ 如果是平稳非白噪声序列就计算ACF（自相关系数）、PACF（偏自相关系数），进行ARMA等模型识别；
④ 对已识别好的模型，确定模型参数，最后应用预测并进行误差分析。

一般地，对于给定的时间序列 ，平稳序列的建模过程可以用下图中的流程图表示。

ARIMA实战剖析

导入必要的库

导入statmodelsPython库已使用ARIMA模型。

import os
import warnings
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import datetime as dt
import math

from pandas.plotting import autocorrelation_plot
from statsmodels.tsa.statespace.sarimax import SARIMAX
from sklearn.preprocessing import MinMaxScaler
from common.utils import load_data, mape
from IPython.display import Image

from statsmodels.graphics.tsaplots import plot_acf, plot_pacf  
from statsmodels.tsa.stattools import adfuller  # adf检验库
from statsmodels.stats.diagnostic import acorr_ljungbox  # 随机性检验库
from statsmodels.tsa.arima_model import ARMA 

%matplotlib inline
plt.rcParams['figure.figsize'] = (12,6)
pd.options.display.float_format = '{:,.2f}'.format
np.set_printoptions(precision=2)
warnings.filterwarnings("ignore") # specify to ignore warning messages

导入数据

energy = pd.read_csv('./data/energy.csv')
energy.head(10)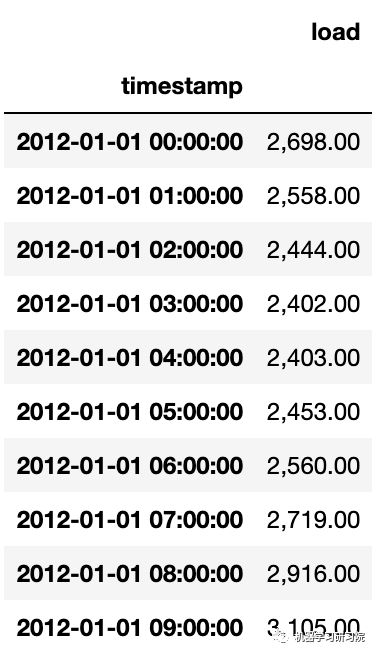

绘制从2012年1月到2014年12月的所有可用能源数据。看到这些数据，并不陌生，因为在之前的文章中已经展示了部分数据。

energy.plot(y='load', subplots=True, 
            figsize=(15, 8), fontsize=12)
plt.xlabel('timestamp', fontsize=12)
plt.ylabel('load', fontsize=12)
plt.show()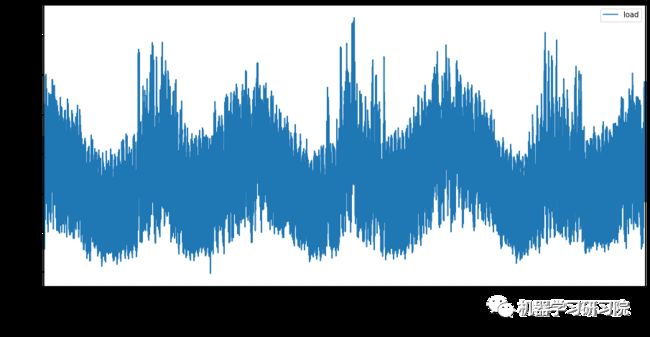

划分训练和测试数据集

现在已经加载了数据，可以将其划分为训练集和测试集。要在训练集上训练模型。通常，在模型完成训练后，将使用测试集评估它的准确性。需要确保测试集涵盖了来自训练集的较晚时间段，以确保模型不会从未来时间段获取信息。

从2014年9月1日到10月31日，分配两个月的时间给训练集。测试集将包括2014年11月1日至12月31日两个月的时间段:

train_start_dt = '2014-11-01 00:00:00'
test_start_dt = '2014-12-30 00:00:00'

由于这一数据反映的是每日能源消费，因此存在强烈的季节性模式，但当前消费与最近几天的消费规律最为相似。

可视化差异

为了更加直观地看出训练集和测试集的差异，我们在同一张图中用不同颜色区分两个测试集，蓝色为训练集、橙色为测试集。

energy[(energy.index < test_start_dt) & (energy.index >= train_start_dt)][['load']].rename(columns={'load':'train'}) \
    .join(energy[test_start_dt:][['load']].rename(columns={'load':'test'}), how='outer') \
    .plot(y=['train', 'test'], figsize=(15, 8), fontsize=12)
plt.xlabel('timestamp', fontsize=12)
plt.ylabel('load', fontsize=12)
plt.show()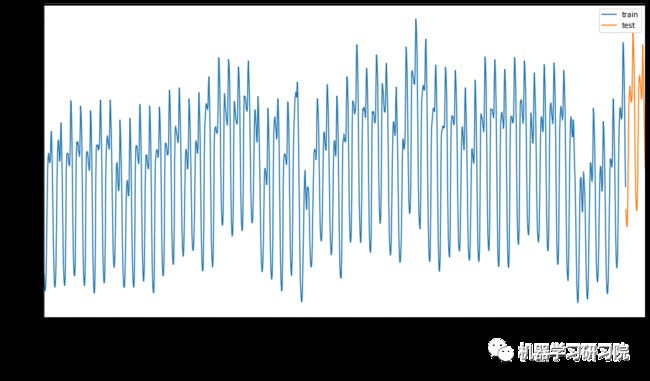

使用一个相对较小的时间窗口来训练数据就足够了。

准备训练数据

现在需要通过对数据进行筛选和归一化来为模型训练准备数据。筛选需要的时间段和列的数据，并且对其进行归一化，其作用的是将数据投影在0-1之间。

① 过滤原始数据集，只包括前面提到的每个set的时间段，只包括所需的列'load'加上日期索引。

train = energy.copy()[(energy.index >= train_start_dt) & (energy.index < test_start_dt)][['load']]
test = energy.copy()[energy.index >= test_start_dt][['load']]

print('Training data shape: ', train.shape)
print('Test data shape: ', test.shape)

Training data shape:  (1416, 1)
Test data shape:  (48, 1)

② 使用MinMaxScaler()对训练数据进行 (0, 1) 标准化。

scaler = MinMaxScaler()
train['load'] = scaler.fit_transform(train)
train.head(10)

③ 原始数据和标准化数据进行可视化比较。

energy[(energy.index >= train_start_dt) & (energy.index < test_start_dt)][['load']].rename(columns={'load':'original load'}).plot.hist(bins=100, fontsize=12)
train.rename(columns={'load':'scaled load'}).plot.hist(bins=100, fontsize=12)
plt.show()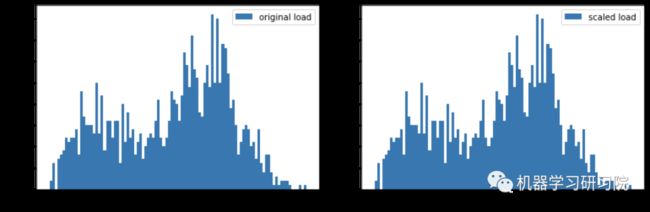

④ 根据训练好的归一化模型，对测试集数据归一化。

test['load'] = scaler.transform(test)
test.head()

稳定性检验

adfuller(Augmented Dickey-Fuller)测试可用于在存在串行相关的情况下在单变量过程中测试单位根。

statsmodels.tsa.stattools.adfuller(x，
maxlag = None，regression ='c'，autolag ='AIC'，
store = False，regresults = False )

adfuller中可进行adf校验，一般传入一个data就行，包括 list, numpy array 和 pandas series都可以作为输入，其他参数可以保留默认。

返回值：

adf（float）
测试统计

pvalue（float）
MacKinnon基于MacKinnon的近似p值（1994年，2010年）

usedlag（int）
使用的滞后数量

nobs（int）
用于ADF回归的观察数和临界值的计算

critical values（dict）
测试统计数据的临界值为1％，5％和10％。基于MacKinnon（2010）

icbest（float）
如果autolag不是None，则最大化信息标准。

resstore （ResultStore，可选）
一个虚拟类，其结果作为属性附加

如何确定该序列能否平稳呢？主要看：

1%、%5、%10不同程度拒绝原假设的统计值和ADF Test result的比较，ADF Test result同时小于1%、5%、10%即说明非常好地拒绝该假设。另外，P-value是否非常接近0，接近0，则是平稳的，否则，不平稳。

若不平稳，则需要进行差分，差分后再进行检测。

def adf_val(ts, ts_title):
    '''
    ts: 时间序列数据，Series类型
    ts_title: 时间序列图的标题名称，字符串
    '''     
    # 稳定性（ADF）检验
    adf, pvalue, usedlag, nobs, critical_values, icbest = adfuller(ts)  

    name = ['adf', 'pvalue', 'usedlag',
            'nobs', 'critical_values', 'icbest']    
    values = [adf, pvalue, usedlag, nobs, 
              critical_values, icbest]  
    print(list(zip(name, values)))

    return adf, pvalue, critical_values,  
    # 返回adf值、adf的p值、三种状态的检验值

用上面定义的函数进行平稳性检验。

# 读取数据
ts_data = df['load'].astype('float32')  
adf, pvalue1, critical_values = adf_val(
          ts_data, 'raw time series')

[('adf', -10.404080285485218), 
('pvalue', 1.876514522339643e-18), 
('usedlag', 49), 
('nobs', 26254), 
('critical_values', {'1%': -3.430599102593299, 
                     '5%': -2.8616500960359854, 
                     '10%': -2.5668286008605627}
                     ), 
('icbest', 265656.2951464001)]

adf结果为-10.4， 小于三个level的统计值。pvalue也是接近于0 的，所以是平稳的。

白噪声检测

白噪声检验也称为纯随机性检验，当数据是纯随机数据时，再对数据进行分析就没有任何意义了，所以拿到数据后最好对数据进行一个纯随机性检验。

# 数据的纯随机性检验函数
acorr_ljungbox(x, lags=None, boxpierce=False, 
               model_df=0, period=None, 
               return_df=True, auto_lag=False)

主要参数

lags为延迟期数，如果为整数，则是包含在内的延迟期数，如果是一个列表或数组，那么所有时滞都包含在列表中最大的时滞中。

boxpierce为True时表示除开返回LB统计量还会返回Box和Pierce的Q统计量

返回值

lbvalue: (float or array)
测试的统计量

pvalue: (float or array)
基于卡方分布的p统计量

bpvalue: ((optionsal), float or array)
基于 Box-Pierce 的检验的p统计量

bppvalue: ((optional), float or array)
基于卡方分布下的Box-Pierce检验的p统计量

若p值远小于0.01，因此我们拒绝原假设，认为该时间序列是平稳的。（这里原假设是存在单位根，即时间序列为非平稳的。)

def acorr_val(ts):
    '''
    # 白噪声（随机性）检验
    ts: 时间序列数据，Series类型
    返回白噪声检验的P值
    '''
    lbvalue, pvalue = acorr_ljungbox(ts, lags=1)  # 白噪声检验结果
    return lbvalue, pvalue
    
acorr_val(ts_data)

24056.19, 0.

ARIMA模型实现

可以使用statsmodels 库创建 ARIMA 模型。并遵循以下几个步骤。

1. 通过调用SARIMAX()并传入模型参数： p, d, q参数，以及 P, D, Q参数定义模型。

2. 通过调用fit()函数为训练数据准备模型。

3. 通过调用forecast()函数进行预测，并指定要预测的步骤数(horizon)。

在ARIMA模型中，有3个参数用于帮助对时间序列的主要方面进行建模：季节性、趋势和噪声。

p：与模型的自回归方面相关的参数，模型中包含的滞后观测数，也称为滞后阶数。
d：与模型集成部分相关的参数，原始观测值差异的次数，也称为差异度。它影响到应用于时间序列的差分的数量。
q：与模型的移动平均部分相关的参数。移动平均窗口的大小，也称为移动平均的阶数。

值 0 可用于参数，表示不使用模型的该元素。这样，ARIMA 模型可以配置为执行 ARMA 模型的功能，甚至是简单的 AR、I 或 MA 模型。

Note: 如果数据具有季节性——我们使用季节性ARIMA模型(SARIMA)。在这种情况下，您需要使用另一组参数:' P '， ' D '和' Q '，它们描述了与' p '， ' d '和' q '相同的关联，不同的是对应于模型的季节性成分。

确定时间序列的差分 

ARIMA 模型对时间序列的要求是平稳型。因此，当你得到一个非平稳的时间序列时，首先要做的即是做时间序列的差分，直到得到一个平稳时间序列。如果你对时间序列做  次差分才能得到一个平稳序列，那么可以使用 模型，其中  是差分次数。

fig = plt.figure(figsize=(20,16))
ax1= fig.add_subplot(211)
diff1 = train.diff(1)
diff1.plot(ax=ax1)
ax2= fig.add_subplot(212)
diff2 = train.diff(2)
diff2.plot(ax=ax2)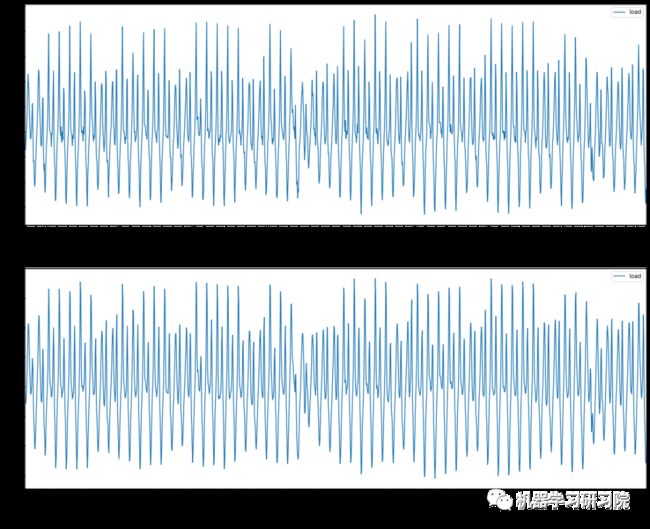

可以看出一阶差分的时间序列的均值和方差已经基本平稳，二阶差分后的时间序列与一阶差分相差不大，并且二者随着时间推移，时间序列的均值和方差保持不变。因此可以将差分次数  设置为1。

确定合适的 

现在我们已经得到一个平稳的时间序列，接来下就是选择合适的ARIMA模型，即ARIMA模型中合适的 。

模式识别

可通过下面的代码，计算自相关系数（Autocorrelation Function, SAF）和偏自相关系数（Partial Autocorrelation Function, PACF）。绘制并检查平稳时间序列的自相关图和偏自相关图。

自相关（Autocorrelation）： 对一个时间序列，现在值与其过去值的相关性。如果相关性为正，则说明现有趋势将继续保持。

偏自相关（Partial Autocorrelation）： 可以度量现在值与过去值更纯正的相关性。
比如，当我们计算  与  的相关性时， 可能会受到  的影响，同时  也会受到  的影响。而偏自相关就是用来计算剔除  影响后， 与  的相关性。

偏自相关的通俗计算过程：

有三个自变量 、、，一个因变量 ：

• 线性回归建模：通过  和  预测 ，取残差

• 线性回归建模：通过  和  预测 ，取残差

• 由于以上两个残差都剔除了  和  的影响，因此对两个残差取相关性就是  与  的偏自相关

如果一个时间序列满足以下两个条件:

•  具有拖尾性，即  不会在  大于某个常数之后就恒等于 0。

•  具有截尾性，即  在  时变为 0。

第 2 个条件还可以用来确定阶数 。考虑到存在随机误差的存在，因此  在  阶延迟后未必严格为 0 ，而是在 0 附近的小范围内波动。具体来说，设  阶偏自相关系数为 ，若阶数大于  大部分的偏自相关系数满足下式，则模型的阶数取 。

其中  表示样本序列长度。

ACF 和 PACF 图： 通过差分对时间序列进行平稳化后，拟合 ARIMA 模型的下一步是确定是否需要 AR 或 MA 项来校正差分序列中剩余的任何自相关。结合自相关图和偏自相关图共同进行判断时间序列模型。

关于ARMA通用判断标准说明如下表格：

模型	自相关图	偏自相关图
AR(p)	拖尾	p阶截尾
MA(q)	q阶截尾	拖尾
ARMA(p,q)	拖尾	拖尾
模型不适合	截尾	截尾

拖尾和截尾说明如下：

拖尾： 始终有非零取值，不会在大于某阶后就快速趋近于0（而是在0附近波动），可简单理解为无论如何都不会为0，而是在某阶之后在0附近随机变化。

截尾： 在大于某阶(k)后快速趋于0为k阶截尾，可简单理解为从某阶之后直接就变为0。

通常情况下:

• 如果说自相关图拖尾，并且偏自相关图在p阶截尾时，此模型应该为AR(p)。

• 如果说自相关图在q阶截尾并且偏自相关图拖尾时，此模型应该为MA(q)。

• 如果说自相关图和偏自相关图均显示为拖尾，那么可结合ACF图中最显著的阶数作为q值，选择PACF中最显著的阶数作为p值，最终建立ARMA(p,q)模型。

• 如果说自相关图和偏自相关图均显示为截尾，那么说明不适合建立ARMA模型。

from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
fig, axes = plt.subplots(2, 1, figsize=(12, 4*2))
# 自相关
plot_acf(data['co2'],lags=12,title='raw_acf', ax=axes[0])  
# 偏自相关
plot_pacf(data['co2'],lags=12,title='raw_pacf', ax=axes[1])  
plt.show()
# 其中lags 表示滞后的阶数，以上分别得到acf 图和pacf 图。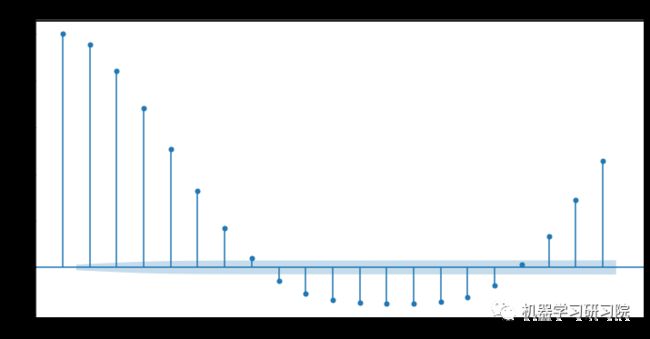

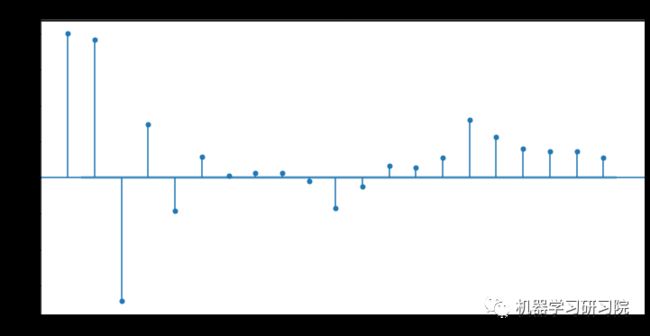
然后根据如下常用准则选择模型：

•  赤池信息量 akaike information criterion

•  贝叶斯信息量 bayesian information criterion

•  hannan-quinn criterion

具体方法可以参考：ACF 和 PACF ^[6]

手动选择超参数

为ARIMA模型的参数选择最佳值可能是一个挑战，因为这有点主观，也有点耗时。可以考虑使用'pyramid'库^[7] 中的 'auto_arima()' 函数。文末提供一种网格搜索方法来自动选择超参数。

本文通过手动选择参数的方式，也许模型效果不是很理想，目的是进行快速演示建模过程。

① 首先设置horizon值。先试试3个小时:

# 指定要提前预测的步骤数
HORIZON = 3
print('Forecasting horizon:', HORIZON, 'hours')

Forecasting horizon: 3 hours

② 现在尝试一些手动选择参数来找到一个相对好的模型。

order = (4, 1, 0)
seasonal_order = (1, 1, 0, 24)

model = SARIMAX(endog=train, order=order, 
                seasonal_order=seasonal_order)
results = model.fit()

print(results.summary())

打印结果。

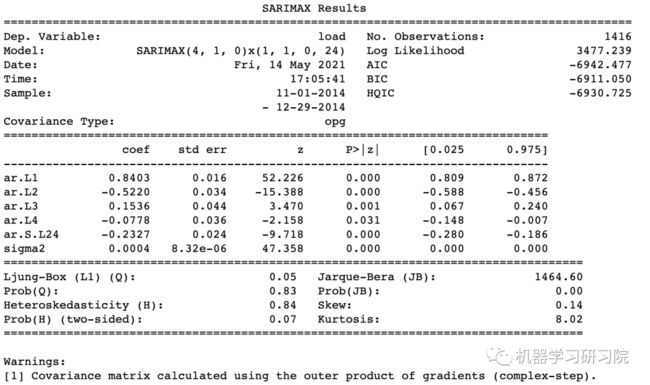
现在已经建立了一个时序模型，现在我们需要找到一种方法来计算它。

模型评估

为了评估模型，可以使用walk forward验证。在实践中，每次有新的数据可用时，时间序列模型都要重新训练。这使得模型可以在每个时间步骤中做出最好的预测。

从使用该技术的时间序列的开始，在训练数据集上训练模型。然后对下一个时间步骤进行预测。根据已知值对预测进行评估。然后将训练集扩展到包含已知值，并重复该过程。

Note: 为了更有效的训练，应该保持训练集窗口固定，以便每次向训练集添加新的观察值时，并将该观察值从集合的开始处删除。

这个过程为模型在实践执行提供了更可靠的估计。然而，这是以创建众多模型的计算成本为代价的。如果数据较小或模型简单的话，这是可以接受的，但如果数据量大，或者模型规模大可能是一个问题。

Walk-forward validation 是时间序列模型评估的黄金标准，可以考虑用于你自己的项目。

① 首先，为每个HORIZON步骤创建一个测试数据点。

test_shifted = test.copy()

for t in range(1, HORIZON+1):
    test_shifted['load+'+str(t)] = test_shifted['load'].shift(-t, freq='H')

test_shifted = test_shifted.dropna(how='any')
test_shifted.head(5)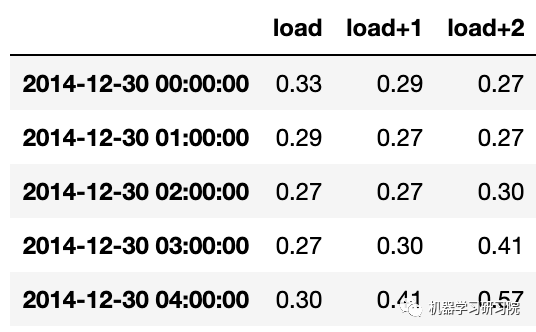

数据根据它的地平线上点水平移动。

② 在循环中使用滑动窗口方法预测测试数据的长度

%%time
training_window = 720 # 投入30天(720小时)进行训练

train_ts = train['load']
test_ts = test_shifted

history = [x for x in train_ts]
history = history[(-training_window):]

predictions = list()

order = (2, 1, 0)
seasonal_order = (1, 1, 0, 24)

for t in range(test_ts.shape[0]):
    model = SARIMAX(endog=history, order=order, seasonal_order=seasonal_order)
    model_fit = model.fit()
    yhat = model_fit.forecast(steps = HORIZON)
    predictions.append(yhat)
    obs = list(test_ts.iloc[t])
    # move the training window
    history.append(obs[0])
    history.pop(0)
    print(test_ts.index[t])
    print(t+1, ': predicted =', yhat, 'expected =', obs)

我们可以看出训练的过程

2014-12-30 00:00:00
1 : predicted = [0.32 0.29 0.28] 
    expected = [0.32945389435989236, 
                0.2900626678603402, 
                0.2739480752014323]

2014-12-30 01:00:00
2 : predicted = [0.3  0.29 0.3 ] 
    expected = [0.2900626678603402, 
                0.2739480752014323, 
                0.26812891674127126]

2014-12-30 02:00:00
3 : predicted = [0.27 0.28 0.32] 
    expected = [0.2739480752014323, 
                0.26812891674127126, 
                0.3025962399283795]

③ 将预测结果与实际负荷进行比较:

eval_df = pd.DataFrame(predictions, columns=['t+'+str(t) for t in range(1, HORIZON+1)])
eval_df['timestamp'] = test.index[0:len(test.index)-HORIZON+1]
eval_df = pd.melt(eval_df, id_vars='timestamp', value_name='prediction', var_name='h')
eval_df['actual'] = np.array(np.transpose(test_ts)).ravel()
eval_df[['prediction', 'actual']] = scaler.inverse_transform(eval_df[['prediction', 'actual']])
eval_df.head()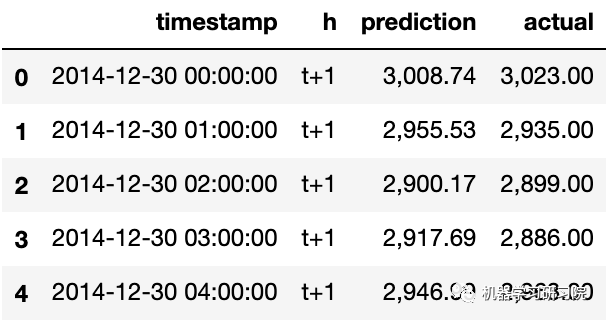

观察每小时数据的预测，并与实际负载进行比较。这有多准确?

评估模型的准确性

通过测试所有预测的平均绝对百分比误差(MAPE)来评估模型的准确性。

MAPE是在一个预测方法的预测精度的测量统计。由上述公式定义。实际和预测的差除以实际。“这个计算的绝对值是对每个预测时间点求和，然后除以拟合点的数目n。” wikipedia^[8]

① 用代码表示方程:

if(HORIZON > 1):
    eval_df['APE'] = (eval_df['prediction'] - eval_df['actual']).abs() / eval_df['actual']
    print(eval_df.groupby('h')['APE'].mean())

② 计算一步的MAPE:

print('One step forecast MAPE: ', 
      (mape(eval_df[eval_df['h'] == 't+1']['prediction'], 
      eval_df[eval_df['h'] == 't+1']['actual'])
      )*100, '%')

One step forecast MAPE:  0.5570581332313952 %

③ 打印多步预测MAPE:

print('Multi-step forecast MAPE: ', 
       mape(eval_df['prediction'], 
       eval_df['actual'])*100, '%')

Multi-step forecast MAPE:  1.1460048657704118 %

结果值较低是很好的：考虑到一个MAPE为10的预测会下降10%。

④ 为更加容易直观地看到这种精度测量，把他们可视化出来。

if(HORIZON == 1):
    ## Plotting single step forecast
    eval_df.plot(x='timestamp', y=['actual', 'prediction'], style=['r', 'b'], figsize=(15, 8))

else:
    ## Plotting multi step forecast
    plot_df = eval_df[(eval_df.h=='t+1')][['timestamp', 'actual']]
    for t in range(1, HORIZON+1):
        plot_df['t+'+str(t)] = eval_df[(eval_df.h=='t+'+str(t))]['prediction'].values

    fig = plt.figure(figsize=(15, 8))
    ax = plt.plot(plot_df['timestamp'], plot_df['actual'], color='red', linewidth=4.0)
    ax = fig.add_subplot(111)
    for t in range(1, HORIZON+1):
        x = plot_df['timestamp'][(t-1):]
        y = plot_df['t+'+str(t)][0:len(x)]
        ax.plot(x, y, color='blue', linewidth=4*math.pow(.9,t), alpha=math.pow(0.8,t))

    ax.legend(loc='best')

plt.xlabel('timestamp', fontsize=12)
plt.ylabel('load', fontsize=12)
plt.show()

综上所述，这个过程的步骤如下：

1. 模型识别。使用绘图和汇总统计来识别趋势、季节性和自回归元素，以了解所需的差异量和滞后大小。

2. 参数估计。使用拟合程序找到回归模型的系数。

3. 模型检查。使用残差的绘图和统计检验来确定模型未捕获的时间结构的数量和类型。

重复该过程，直到在样本内或样本外观察（例如训练或测试数据集）上达到理想的拟合水平。

网格搜索选择超参数

将网格搜索定义为一个函数evaluate_arima_model()，该函数以时间序列数据集作为输入，以及元组(p,d,q)作为参数用于评估模型。

数据集分为两部分：初始训练数据集为 66％，测试数据集为剩余的 34％。

迭代测试集的每个时间步。一次迭代就可以训练一个模型，然后使用该模型对新数据进行预测。每次迭代都进行预测并存储在列表中。最后用测试集将所有预测值与预期值列表进行比较，并计算并返回均方误差分数。

# evaluate an ARIMA model for a given order (p,d,q)
def evaluate_arima_model(X, arima_order):
 # prepare training dataset
 train_size = int(len(X) * 0.66)
 train, test = X[0:train_size], X[train_size:]
 history = [x for x in train]
 # make predictions
 predictions = list()
 for t in range(len(test)):
  model = ARIMA(history, order=arima_order)
  model_fit = model.fit(disp=0)
  yhat = model_fit.forecast()[0]
  predictions.append(yhat)
  history.append(test[t])
 # calculate out of sample error
 error = mean_squared_error(test, predictions)
 return error

继续定义一个evaluate_models()的函数，该函数为ARIMA指定(p,d,q)参数，并以网格循环到方式进行迭代。

# evaluate combinations of p, d and q values for an ARIMA model
def evaluate_models(dataset, p_values, d_values, q_values):
  # 确保输入数据是浮点值（而不是整数或字符串）
 dataset = dataset.astype('float32')
 best_score, best_cfg = float("inf"), None
 for p in p_values:
  for d in d_values:
   for q in q_values:
    order = (p,d,q)
    try:
     mse = evaluate_arima_model(dataset, order)
     if mse < best_score:
      best_score, best_cfg = mse, order
     print('ARIMA%s MSE=%.3f' % (order,mse))
    except:
     continue
 print('Best ARIMA%s MSE=%.3f' % (best_cfg, best_score))

参考资料

[1] 

ARIMA 模型: https://people.duke.edu/~rnau/411arim.htm

[2] 

autoRegressive I integrated Moving a average: https://wikipedia.org/wiki/Autoregressive_integrated_moving_average

[3] 

AR自回归: https://wikipedia.org/wiki/Autoregressive_integrated_moving_average

[4] 

综合: https://wikipedia.org/wiki/Order_of_integration

[5] 

移动平均: https://wikipedia.org/wiki/Moving-average_model

[6] 

ACF 和 PACF : https://people.duke.edu/~rnau/411arim3.htm

[7] 

'pyramid'库: https://alkaline-ml.com/pmdarima/0.9.0/modules/generated/pyramid.arima.auto_arima.html

[8] 

wikipedia: https://wikipedia.org/wiki/Mean_absolute_percentage_error

往期精彩回顾




适合初学者入门人工智能的路线及资料下载机器学习及深度学习笔记等资料打印机器学习在线手册深度学习笔记专辑《统计学习方法》的代码复现专辑
AI基础下载黄海广老师《机器学习课程》视频课黄海广老师《机器学习课程》711页完整版课件

本站qq群554839127，加入微信群请扫码：