基于Matlab的滑动窗FFT算法实现

目录

前言：

1.1 滑动窗FFT算法推导

1.2 滑动窗FFT算法实现 

1.3 结论

---

前言：

作为一个在研狗，开源一个工程信息学小作业，是关于滑动窗FFT算法的推导和实现的，实现借助Matlab2018a实现。

---

1.1 滑动窗FFT算法推导

用表示输入序列段的N点FFT，由FFT的定义可以得到：

 以及：

  将P=n+1带入公式（2），可以将公式写成：

 将和式展开，和式标号加以改变，可以得到：

 将指数因子展开得到：

 

注意到指数项的周期性并用代替和式，可以简化表达式并推出FFT的计算形式：

  

公式(6)表明：第k+1次采样的FFT等于先前的FFT和最新样值与最早样值之差(也就是迸入窗口前沿的样值与离开后沿的样值之差)的相移和。

因此,如果知道k时输入序列的变换,就可以推导出下一序列的变换(k+1时),而不用计算另外的FFT。只需N次复数乘法和N次复数加法,就可以从计算。相比之下,重新计算FFT需要次乘法运算和次加法运算。滑动FFT的另一个优点是它不需要位反转,这与许多FFT算法不同。

---

1.2 滑动窗FFT算法实现 

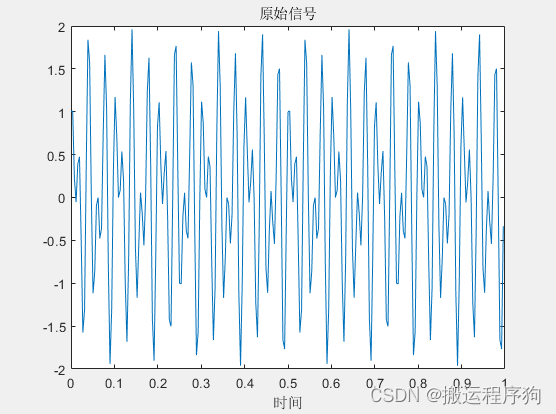
在本代码中首先利用Matlab产生一个xx=cos(100*pi*t)+sin(60*pi*t)的原始信号并绘制其原始图像；然后对原始信号直接进行256点的FFT算法得到其频谱图并进行绘制；最后对原始信号进行256点的SFFT算法得到该算法的实现过程的gif图。实现代码如下：

clear;clc;close all 
nn=256;
sf1=256;
t=0:1/sf1:255/sf1;
%% FFT分析
xx=cos(100*pi*t)+sin(60*pi*t); %获取数据
figure(1)
plot(t,xx) %绘制原始信号
xlabel('时间'),title('原始信号')
y=fft(xx, nn);               %计算FFT
figure(2)
plot(abs(y))                 %绘图
xlim([0 255]) % 调整坐标范围
xlabel('点数')，title('FFT分析256点')
 
%% SFFT实现，生成gif图
%空矩阵的作用是作为SFFT的初值
x1=zeros(1,nn); %建立空矩阵，
y1=zeros(1,nn); %建立空矩阵
k=0:1:nn-1;     %用于计算u矩阵
u=exp(1i*2*pi*k/nn);
pic_num=1;
for t1=0:1/sf1:255/sf1
    a=cos(100*pi*t1)+sin(60*pi*t1);     %新数据输入
    x1(length(x1)+1)=a;                 %开辟一个空间将新数据加入队列尾
    b=x1(1);                            %从队列头取出一个数据
    x1(1)=[];                           %删除存放上面取出的数据空间
    for i1=1:nn                         %计算SFFT，循环次数等于N=256
       y1(i1)= u(i1)*(y1(i1)-b+x1(nn)); %计算k=0,1,2...N-1的频域值
    end
    figure(3)
    plot(k, abs(y1));                   %绘图
    xlim([0 255])                       % 调整坐标范围
xlabel('点数'),title('SFFT分析256点')
    drawnow;                            %生成gif代码，输出在此m文件目录下面
    F=getframe(gcf);
    I=frame2im(F);
    [I,map]=rgb2ind(I,256);
    if pic_num == 1       imwrite(I,map,'test.gif','gif','Loopcount',inf,'DelayTime',0.1);
    else    imwrite(I,map,'test.gif','gif','WriteMode','append','DelayTime',0.1);
    end
    pic_num = pic_num + 1;
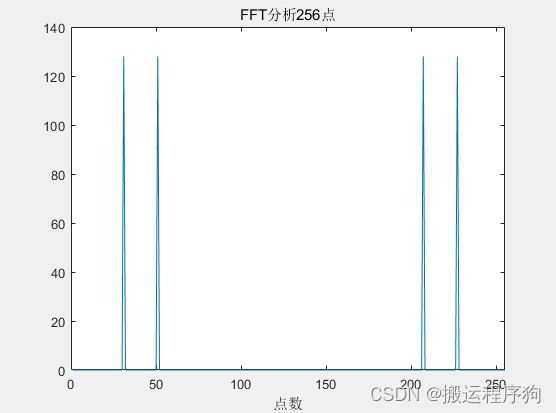
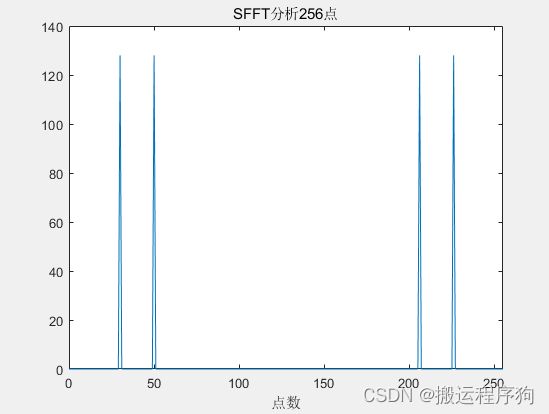
end

生成的原始信号图如图3.1所示，生成的256点FFT频谱图如图3.2所示，生成的256点SFFT的Gif图如图3.3所示，SFFT最后生成的256点频谱图如图3.4所示，最后发现前后两种算法生成的256点频谱图一致，验证了SFFT算法的正确性。

 图3.1 原始信号的图

 

 图3.2 256点FFT频谱图

 

 图3.3 256点SFFT的Gif图 

 图3.4 256点SFFT频谱图

1.3 结论

通过在Matlab上的仿真，可以清晰的感受到利用SFFT进行信号频谱的分析要比直接利用FFT进行频谱分析实时性要好，只要输入数据发生改变时，FFT就需要重新进行计算，而SFFT可以由之前计算的FFT结果进行推导，实时性要好，相对于直接进行FFT计算量要少。