lstm时间序列预测python_Keras中的多变量时间序列预测-LSTMs
神经网络诸如长短期记忆(LSTM)递归神经网络,几乎可以无缝地对多变量输入问题进行建模。
这在时间预测问题中非常有用,而经典线性方法难以应对多变量预测问题。
在本教程中,您将了解如何在Keras深度学习库中,为多变量时间序列预测开发LSTM模型。
学习该教程后,您将收获:
如何将原始数据集转换为可用于时间序列预测的数据集;
如何准备数据,并使LSTM模型适用于多变量时间序列预测问题;
如何做预测,并将预测的结果重新调整为原始数据单位。
让我们开始吧!
教程概括
该教程分为3部分,包括:
空气污染预测
数据准备
多变量LSTM预测模型
Python环境
你可以使用Python 2 或Python 3,需要安装scikit-learn、Numpy、Pandas、Matplotlib、 Scipy、Keras(2.0或更高版本)、TensorFlow或Theano backend等依赖包。
本试验在Anaconda Jupyter Notebook中进行,上述大部分依赖包均已内置,但仍需要安装单独安装TensorFlow、Theano backend。
如果你有任何问题:
请看这篇教程:如何在Anaconda中配置Python环境,进行机器学习和深度学习
1.空气污染预测
该教程中,我们将使用空气质量数据集。
该数据集字段包括日期时间、PM2.5浓度、露点、温度、风向、风速、雨雪累计小时数等,完整特征列表如下:
No:行号
year:该行记录的年
month:该行记录的月
day:该行记录的日
hour:该行记录的小时
pm2.5:PM2.5浓度(细颗粒物指环境空气中空气动力学当量直径小于等于 2.5微米的颗粒物。它能较长时间悬浮于空气中,其在空气中含量浓度越高,就代表空气污染越严重)
DEWP:露点(又称露点温度(Dew point temperature),在气象学中是指在固定气压之下,空气中所含的气态水达到饱和而凝结成液态水所需要降至的温度)
TEMP:温度
PRES:大气压力
cbwd:组合风向
lws:累计风速
ls:累计小时下雪量
lr:累计小时下雨量
该数据记录了北京某段时间每小时的气象情况和污染程度,我们将根据前几个小时的记录预测下个小时的污染程度。
你可以下载该数据集,或在线使用:
北京PM2.5数据集
2.数据准备
我们先看看数据长什么样:
yearmonthdayhourpm2.5DEWPTEMPPREScbwdIwsIsIr
No
12010110NaN-21-11.01021.0NW1.7900
22010111NaN-21-12.01020.0NW4.9200
32010112NaN-21-11.01019.0NW6.7100
42010113NaN-21-14.01019.0NW9.8400
52010114NaN-20-12.01018.0NW12.9700
可以看到日期和时间是分开的,第一步把日期时间合并为一个datetime,以便将其作为Pandas里的索引。
看数据表可知,第一个24小时里,PM2.5这一列有很多空值。因此,我们把第一个24小时里的数据行删掉。剩余的数据里面也有少部分空值,为了保持数据完整性和连续性,只要将空值填补为0即可。
下面的脚本加载了原始数据集,并将日期时间合并解析为Pandas DataFrame索引。删除No(序号)列,给剩下的列重新命名字段。最后替换空值为0,删除第一个24小时数据行。
from pandas import read_csv
from datetime import datetime
# 加载数据
def parse(x):
return datetime.strptime(x, '%Y %m %d %H')
dataset = read_csv('https://raw.githubusercontent.com/jbrownlee/Datasets/master/pollution.csv', parse_dates = [['year', 'month', 'day', 'hour']], index_col=0, date_parser=parse)
#删除No列
dataset.drop('No', axis=1, inplace=True)
# 修改剩余列名称
dataset.columns = ['pollution', 'dew', 'temp', 'press', 'wnd_dir', 'wnd_spd', 'snow', 'rain']
dataset.index.name = 'date'
# 将所有空值替换为0
dataset['pollution'].fillna(0, inplace=True)
# 删除前24小时行
dataset = dataset[24:]
# 打印前5行
print(dataset.head(5))
# 保存数据到pollution.csv
dataset.to_csv('pollution.csv')
打印前5行,并将数据保存到pollution.csv,看一下:
pollution dew temp press wnd_dir wnd_spd snow rain
date
2010-01-02 00:00:00 129.0 -16 -4.0 1020.0 SE 1.79 0 0
2010-01-02 01:00:00 148.0 -15 -4.0 1020.0 SE 2.68 0 0
2010-01-02 02:00:00 159.0 -11 -5.0 1021.0 SE 3.57 0 0
2010-01-02 03:00:00 181.0 -7 -5.0 1022.0 SE 5.36 1 0
2010-01-02 04:00:00 138.0 -7 -5.0 1022.0 SE 6.25 2 0
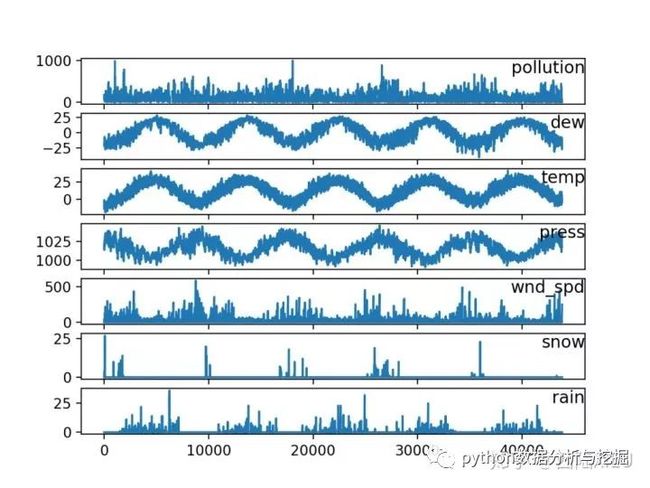
现在我们已经获得了易于使用的数据形式,接下来创建每一特征的分布图表,看看数据长什么样。
加载pollution.csv文件,分别单独绘制每一特征分布图表,风向这一特征是类别特征,不需要绘图的。
from pandas import read_csv
from matplotlib import pyplot
#方便在浏览器中显示图标
%matplotlib inline
# 加载数据
dataset = read_csv('pollution.csv', header=0, index_col=0)
values = dataset.values
# 选择指定列绘图
groups = [0, 1, 2, 3, 5, 6, 7]
i = 1
# 为每一列绘制图表
pyplot.figure()
for group in groups:
pyplot.subplot(len(groups), 1, i)
pyplot.plot(values[:, group])
pyplot.title(dataset.columns[group], y=0.5, loc='right')
i += 1
pyplot.show()
北京空气污染时间序列线性图
3.多变量LSTM预测模型
本节中,我们将LSTM应用到实际问题中。
LSTM数据准备
第一步为LSTM模型准备数据
将数据集构建为监督学习问题,并且对输入变量进行标准化。
在给定污染测量标准和前1个小时污染状况的前提下,我们将构建监督学习问题以预测现在时段的污染情况。
该构想实现起来很简单,只是为了做个示范。你也可以探索其它设想,比如:
基于天气状况和前24小时污染情况,预测下个小时污染情况
如上预测下一个小时污染情况,并给出下一个小时的预期天气状况
我们可以使用series_to_supervised()函数,将数据集构建成适用于监督学习的形式。
首先,加载pollution.csv数据集。对风速特征进行整数编码,即类别标签编码。这可以使用独热向量编码技术,详情可见Python数据分析-类别数据的转换。
接下来,对所有特征数据标准化处理,删去被预测的这一时段的天气特征,完整代码如下:
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import MinMaxScaler
from pandas import DataFrame
from pandas import concat
# 将数据转换成监督学习问题
def series_to_supervised(data, n_in=1, n_out=1, dropnan=True):
n_vars = 1 if type(data) is list else data.shape[1]
df = DataFrame(data)
cols, names = list(), list()
# 输入序列(t-n, ... t-1)
for i in range(n_in, 0, -1):
cols.append(df.shift(i))
names += [('var%d(t-%d)' % (j+1, i)) for j in range(n_vars)]
# 预测序列(t, t+1, ... t+n)
for i in range(0, n_out):
cols.append(df.shift(-i))
if i == 0:
names += [('var%d(t)' % (j+1)) for j in range(n_vars)]
else:
names += [('var%d(t+%d)' % (j+1, i)) for j in range(n_vars)]
# 把所有放在一起
agg = concat(cols, axis=1)
agg.columns = names
# 删除空值行
if dropnan:
agg.dropna(inplace=True)
return agg
# 加载数据
dataset = read_csv('pollution.csv', header=0, index_col=0)
values = dataset.values
# 对风向特征整数标签化
encoder = LabelEncoder()
values[:,4] = encoder.fit_transform(values[:,4])
# 确保所有数据是浮点数类型
values = values.astype('float32')
# 对特征标准化
scaler = MinMaxScaler(feature_range=(0, 1))
scaled = scaler.fit_transform(values)
# 构建成监督学习问题
reframed = series_to_supervised(scaled, 1, 1)
# 删除我们不想预测的天气数据列,只留下pollution列
reframed.drop(reframed.columns[[9,10,11,12,13,14,15]], axis=1, inplace=True)
print(reframed.head())
运行代码,打印出前5行已转换的数据集。我们可以看到8个输入变量 var1(t-1)~var8(t-1) ,这是前一个小时天气情况和污染情况,还有一个输出变量,是当前小时的污染情况。如下:
var1(t-1) var2(t-1) var3(t-1) var4(t-1) var5(t-1) var6(t-1) \
1 0.129779 0.352941 0.245902 0.527273 0.666667 0.002290
2 0.148893 0.367647 0.245902 0.527273 0.666667 0.003811
3 0.159960 0.426471 0.229508 0.545454 0.666667 0.005332
4 0.182093 0.485294 0.229508 0.563637 0.666667 0.008391
5 0.138833 0.485294 0.229508 0.563637 0.666667 0.009912
var7(t-1) var8(t-1) var1(t)
1 0.000000 0.0 0.148893
2 0.000000 0.0 0.159960
3 0.000000 0.0 0.182093
4 0.037037 0.0 0.138833
5 0.074074 0.0 0.109658
数据准备过程比较简单,但有一些知识点可以另外深入研究下。比如:
对风向进行独热向量编码操作
通过差分和季节性调整平稳所有series
把前多个小时的输入作为变量预测该时段的情况
考虑到在学习序列预测问题时,LSTM在时间上使用反向传播,最后一点可能是最重要的。
定义和拟合模型
这一部分,我们将会在多变量输入数据上拟合LSTM模型。
第一步,分割训练集和测试集。为了加快这个演示模型的训练,我们仅仅在第1年数据上拟合模型,然后在剩余4年的数据上对其进行评估。如果你有时间,可以试试倒置一下,在前4年数据做训练,最后1年数据做测试。
下面的示例将数据集拆分为训练集和测试集,然后将训练集和测试集分别拆分为输入和输出变量。最后将输入变量(X)转变成LSTMs需要的三维格式,即[samples,timesteps,features]。
# 切分训练集和测试机
values = reframed.values
n_train_hours = 365 * 24
train = values[:n_train_hours, :]
test = values[n_train_hours:, :]
# 切分输入和输出
train_X, train_y = train[:, :-1], train[:, -1]
test_X, test_y = test[:, :-1], test[:, -1]
# 将输入转换为三维格式 [samples, timesteps, features]
train_X = train_X.reshape((train_X.shape[0], 1, train_X.shape[1]))
test_X = test_X.reshape((test_X.shape[0], 1, test_X.shape[1]))
print(train_X.shape, train_y.shape, test_X.shape, test_y.shape)
执行上面代码后,打印出训练集和测试集输出、输出数据的规格,大约9K小时的数据用于训练,大约35K小时的数据用于测试。
(8760, 1, 8) (8760,) (35039, 1, 8) (35039,)
现在开始定义和拟合LSTM模型
第一个隐藏层中有50个神经元,输出层中有1个神经元用于预测污染情况,输入变量为一小时里的8个天气和污染特征。
我们将使用平均绝对误差损失函数,以及随机梯度下降高效Adam版本。
该模型训练50次,批量大小为72。请记住,Kearas中LSTM的内部状态在每个训练批次结束后重置,所以作为若干天函数的内部状态可能会有作用。
最后,我们通过在fit()函数中设置validation_data参数来跟踪训练期间的训练和测试损失。在运行结束时,绘制训练和测试损失趋势线。
from sklearn.metrics import mean_squared_error
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
# 设计模型
model = Sequential()
model.add(LSTM(50, input_shape=(train_X.shape[1], train_X.shape[2])))
model.add(Dense(1))
model.compile(loss='mae', optimizer='adam')
# 拟合模型
history = model.fit(train_X, train_y, epochs=50, batch_size=72, validation_data=(test_X, test_y), verbose=2, shuffle=False)
# 绘制损失趋势线
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
pyplot.show()
可以看到,测试损失低于训练损失,该模型可能过度拟合训练数据。
评估模型
拟合模型后,开始预测测试集。
将预测结果与测试集结合起来,并反转缩放。还将测试集真实的污染结果数据和测试集结合起来,进行反转缩放。
通过对比原始比例的预测值和实际值,我们可以计算模型的误差分数,这里计算误差用均方根误差。
from numpy import concatenate
from keras.layers import LSTM
from math import sqrt
# 开始预测
yhat = model.predict(test_X)
test_X = test_X.reshape((test_X.shape[0], test_X.shape[2]))
# 预测值反转缩放
inv_yhat = concatenate((yhat, test_X[:, 1:]), axis=1)
inv_yhat = scaler.inverse_transform(inv_yhat)
inv_yhat = inv_yhat[:,0]
# 实际值反转缩放
test_y = test_y.reshape((len(test_y), 1))
inv_y = concatenate((test_y, test_X[:, 1:]), axis=1)
inv_y = scaler.inverse_transform(inv_y)
inv_y = inv_y[:,0]
# 计算均方根误差
rmse = sqrt(mean_squared_error(inv_y, inv_yhat))
print('Test RMSE: %.3f' % rmse)
打印出结果:
Test RMSE: 26.455
最后给出完整代码:
import pandas as pd
from pandas import read_csv
from datetime import datetime
from pandas import read_csv
from matplotlib import pyplot
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import MinMaxScaler
from pandas import DataFrame
from pandas import concat
from sklearn.metrics import mean_squared_error
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
from numpy import concatenate
from keras.layers import LSTM
from math import sqrt
data = pd.read_csv("https://raw.githubusercontent.com/jbrownlee/Datasets/master/pollution.csv",index_col=0)
data.head()
data.to_csv("raw.csv")
# 加载数据
def parse(x):
return datetime.strptime(x, '%Y %m %d %H')
dataset = read_csv('https://raw.githubusercontent.com/jbrownlee/Datasets/master/pollution.csv', parse_dates = [['year', 'month', 'day', 'hour']], index_col=0, date_parser=parse)
#删除No列
dataset.drop('No', axis=1, inplace=True)
# 修改剩余列名称
dataset.columns = ['pollution', 'dew', 'temp', 'press', 'wnd_dir', 'wnd_spd', 'snow', 'rain']
dataset.index.name = 'date'
# 将所有空值替换为0
dataset['pollution'].fillna(0, inplace=True)
# 删除前24小时行
dataset = dataset[24:]
# 打印前5行
print(dataset.head(5))
# 保存数据到pollution.csv
dataset.to_csv('pollution.csv')
#方便在浏览器中显示图标
%matplotlib inline
# 加载数据
dataset = read_csv('pollution.csv', header=0, index_col=0)
values = dataset.values
# 选择指定列绘图
groups = [0, 1, 2, 3, 5, 6, 7]
i = 1
# 为每一列绘制图表
pyplot.figure()
for group in groups:
pyplot.subplot(len(groups), 1, i)
pyplot.plot(values[:, group])
pyplot.title(dataset.columns[group], y=0.5, loc='right')
i += 1
pyplot.show()
# 将数据转换成监督学习问题
def series_to_supervised(data, n_in=1, n_out=1, dropnan=True):
n_vars = 1 if type(data) is list else data.shape[1]
df = DataFrame(data)
cols, names = list(), list()
# 输入序列(t-n, ... t-1)
for i in range(n_in, 0, -1):
cols.append(df.shift(i))
names += [('var%d(t-%d)' % (j+1, i)) for j in range(n_vars)]
# 预测序列(t, t+1, ... t+n)
for i in range(0, n_out):
cols.append(df.shift(-i))
if i == 0:
names += [('var%d(t)' % (j+1)) for j in range(n_vars)]
else:
names += [('var%d(t+%d)' % (j+1, i)) for j in range(n_vars)]
# 把所有放在一起
agg = concat(cols, axis=1)
agg.columns = names
# 删除空值行
if dropnan:
agg.dropna(inplace=True)
return agg
# 加载数据
dataset = read_csv('pollution.csv', header=0, index_col=0)
values = dataset.values
# 对风向特征整数标签化
encoder = LabelEncoder()
values[:,4] = encoder.fit_transform(values[:,4])
# 确保所有数据是浮点数类型
values = values.astype('float32')
# 对特征标准化
scaler = MinMaxScaler(feature_range=(0, 1))
scaled = scaler.fit_transform(values)
# 构建成监督学习问题
reframed = series_to_supervised(scaled, 1, 1)
# 删除我们不想预测的天气数据列,只留下pollution列
reframed.drop(reframed.columns[[9,10,11,12,13,14,15]], axis=1, inplace=True)
print(reframed.head())
# 切分训练集和测试机
values = reframed.values
n_train_hours = 365 * 24
train = values[:n_train_hours, :]
test = values[n_train_hours:, :]
# 切分输入和输出
train_X, train_y = train[:, :-1], train[:, -1]
test_X, test_y = test[:, :-1], test[:, -1]
# 将输入转换为三维格式 [samples, timesteps, features]
train_X = train_X.reshape((train_X.shape[0], 1, train_X.shape[1]))
test_X = test_X.reshape((test_X.shape[0], 1, test_X.shape[1]))
print(train_X.shape, train_y.shape, test_X.shape, test_y.shape)
# 设计模型
model = Sequential()
model.add(LSTM(50, input_shape=(train_X.shape[1], train_X.shape[2])))
model.add(Dense(1))
model.compile(loss='mae', optimizer='adam')
# 拟合模型
history = model.fit(train_X, train_y, epochs=50, batch_size=72, validation_data=(test_X, test_y), verbose=2, shuffle=False)
# 绘制损失趋势线
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
pyplot.show()
# 开始预测
yhat = model.predict(test_X)
test_X = test_X.reshape((test_X.shape[0], test_X.shape[2]))
# 预测值反转缩放
inv_yhat = concatenate((yhat, test_X[:, 1:]), axis=1)
inv_yhat = scaler.inverse_transform(inv_yhat)
inv_yhat = inv_yhat[:,0]
# 实际值反转缩放
test_y = test_y.reshape((len(test_y), 1))
inv_y = concatenate((test_y, test_X[:, 1:]), axis=1)
inv_y = scaler.inverse_transform(inv_y)
inv_y = inv_y[:,0]
# 计算均方根误差
rmse = sqrt(mean_squared_error(inv_y, inv_yhat))
print('Test RMSE: %.3f' % rmse)
注:本文翻译自Jason Brownlee博士的博客