基于遗传算法的图像二值化
基于遗传算法的图像二值化
一、目标
本实验采用遗传算法和大津算法确定图像二值化的最佳阈值,从而对图像进行二值化分割
二、大津算法(最大类间方差法)
最大类间方差法是1979年由日本学者大津提出的,是一种自适应阈值确定的方法,又叫大津法,简称OTSU,是一种基于全局的二值化算法。它是根据图像的灰度特性, 将图像分为前景和背景两个部分。当取最佳阈值时,两部分之间的差别应该是最大的,在OTSU算法中所采用的衡量差别的标准就是较为常见的最大类间方差。前景和背景之间的类间方差如果越大,就说明构成图像的两个部分之间的差别越大,当部分目标被错分为背景或部分背景被错分为目标,都会导致两部分差别变小,当所取阈值的分割使类间方差最大时就意味着错分概率最小。
三通道 rgb 图像转化为灰度图像,
最佳阈值 0-255
三、概念
3.1 灰度直方图概念
灰度直方图是一个像素分布函数,基于每个灰度级(0-255)。横轴是灰度级0-255,纵轴是图像中每个灰度级像素点的数量。
灰度直方图特点: 把整个图像浓缩在直方图中,丢失了所有的空间信息;灰度直方图按照x轴进行积分,就是图像的面积。
灰度直方图应用:
(1)设置图像的参数:
(2)分析图像灰度的变化,确定最优二值化的值:因为灰度直方图通常有一个属性,双峰性(bimodal)(一个称为前景峰值,另一个为背景峰值)。通常两个峰值之间的最小值,为我们想找的最优二值化的分界点
3.2 灰度
灰度是表明图像明暗的数值,即黑白图像中点的颜色深度,范围一般从0到255,白色为
255,黑色为0,故黑白图片也称灰度图像。灰度值指的是单个像素点的亮度。灰度值越
大表示越亮。
3.3 图像灰度化
灰度就是没有色彩,RGB色彩分量全部相等。图像的灰度化就是让像素点矩阵中的每一个像素点都满足关系:R=G=B,此时的这个值叫做灰度值。如 RGB(100,100,100) 就代表灰度值为100, RGB(50,50,50) 代表灰度值为50。
3.4 灰度化处理
一般灰度化处理的方法:在灰度化的图像中灰度值的范围为0~255,
-
浮点算法:Gray=R * 0.3 + G * 0.59 + B *0.11 R=G=B
-
整数方法:Gray=(R * 30+G *59+B *11) / 100 R=G=B
-
移位方法:Gray =(R * 28+G * 151+B * 77)>>8 R=G=B
-
平均值法:Gray=(R+G+B)/3 R=G=B
-
仅取绿色:Gray=G R=G=B
3.5 二值化处理
二值化就是让图像的像素点矩阵中的每个像素点的灰度值为0(黑色)或者255(白色),也就是让整个图像呈现只有黑和白的效果。
-
取阀值为127(相当于0~255的中数,(0+255)/2=127),让灰度值小于等于127的变 为0(黑色),灰度值大于127的变为255(白色),这样做的好处是计算量小速度快,但是 缺点也是很明显的,因为这个阀值在不同的图片中均为127,但是不同的图片,他们的颜色分布差别很大,所以用127做阀值,白菜萝卜一刀切,效果肯定是不好的。
-
计算像素点矩阵中的所有像素点的灰度值的平均值avg
(像素点1灰度值+…+像素点n灰度值)/ n = 像素点平均值avg, 然后让每一个像素点与avg一 一比较,小于等于avg的像素点就为0(黑色),大于avg的 像 素点为255(白色),这样做比方法1好一些。
-
使用直方图方法(也叫双峰法)来寻找二值化阀值,直方图是图像的重要特质。直方图方法 认为图像由前景和背景组成,在灰度直方图上,前景和背景都形成高峰,在双峰之间的最低谷处就是阀值所在。取到阀值之后再一 一比较就可以了。
-
最大类间方差法(大津算法OTSU)是一种基于全局的二值化算法
原理
设图像最佳阈值为T,T将图像分为(前景)目标和背景。其中目标点数占总图像比例为 w 0 w_0 w0,平均灰度值为 u 0 u_0 u0,背景点数占图像比例为 w 1 w_1 w1,平均灰度值为 u 1 u_1 u1。
则 w 0 + w 1 = 1 w_0+ w_1=1 w0+w1=1 (公式1)
则图像的总平均灰度值为: u = w 0 u 0 + w 1 u 1 u= w_0 u_0+ w_1 u_1 u=w0u0+w1u1 (公式2)
类间方差为: g = w 0 ( u 0 − u ) 2 + w 1 ( u 1 − u ) 2 g=w_0 (u_0-u)^2+ w_1 (u_1-u)^2 g=w0(u0−u)2+w1(u1−u)2 (公式3)
可等价为: g = w 0 w 1 ( u 0 − u 1 ) 2 g=w_0 w_1 (u_0-u_1 )^2 g=w0w1(u0−u1)2 (公式4)
公式4推导过程: g = w 0 ( u 0 − u ) 2 + w 1 ( u 1 − u ) 2 g=w_0 (u_0-u)^2+ w_1 (u_1-u)^2 g=w0(u0−u)2+w1(u1−u)2
= w 0 ( u 0 − w 0 u 0 − w 1 u 1 ) 2 + w 1 ( u 1 − w 0 u 0 − w 1 u 1 ) 2 = w_0 (u_0-w_0 u_0-w_1 u_1 )^2+ w_1 (u_1-w_0 u_0-w_1 u_1 )^2 =w0(u0−w0u0−w1u1)2+w1(u1−w0u0−w1u1)2
= w 0 ( ( 1 − w 0 ) u 0 − w 1 u 1 ) 2 + w 1 ( ( 1 − w 1 ) u 1 − w 0 u 0 ) 2 = w_0 ((1-w_0)u_0-w_1 u_1 )^2+ w_1 ((1-w_1)u_1-w_0 u_0 )^2 =w0((1−w0)u0−w1u1)2+w1((1−w1)u1−w0u0)2
= w 0 ( w 1 u 0 − w 1 u 1 ) 2 + w 1 ( w 0 u 1 − w 0 u 0 ) 2 = w_0 (w_1 u_0-w_1 u_1 )^2+ w_1 (w_0 u_1-w_0 u_0 )^2 =w0(w1u0−w1u1)2+w1(w0u1−w0u0)2
= w 0 ( w 1 ( u 0 − u 1 ) ) 2 + w 1 ( w 0 ( u 1 − u 0 ) ) 2 = w_0 (w_1 (u_0-u_1 ))^2+ w_1 (w_0 (u_1-u_0))^2 =w0(w1(u0−u1))2+w1(w0(u1−u0))2
= w 0 w 1 2 ( u 0 − u 1 ) 2 + w 1 w 0 2 ( u 1 − u 0 ) 2 = w_0 w_1^2 (u_0-u_1 )^2+ w_1 w_0^2 (u_1-u_0 )^2 =w0w12(u0−u1)2+w1w02(u1−u0)2
= ( w 0 + w 1 ) w 0 w 1 ( u 0 − u 1 ) 2 = (w_0+w_1)w_0 w_1 (u_0-u_1 )^2 =(w0+w1)w0w1(u0−u1)2
= w 0 w 1 ( u 0 − u 1 ) 2 = w_0 w_1 (u_0-u_1 )^2 =w0w1(u0−u1)2
代码
main.py
import matplotlib.pyplot as plt
import numpy as np
import cv2 as cv
from GA import GA
from timeit import default_timer as timer
if __name__ == '__main__':
tic = timer()
# 待测试的代码
image = cv.imread("11.jpg")
image_gray = cv.cvtColor(image, cv.COLOR_BGR2GRAY) # 以灰度方法读取图像
image_RGB = cv.cvtColor(image, cv.COLOR_BGR2RGB)
# opencv 库计算灰度图像直方图 cv.calcHist(images, channels, mask, histSize, ranges[, hist[, accumulate]])
hist = cv.calcHist([image_gray], [0], None, [256], [0, 256]) # 计算图像的灰度直方图
times = 30 # 迭代次数
ga = GA(hist, 30)
for i in range(times):
ga.evolution()
threshold = ga.threshold()
img_f = image_gray
img_f[img_f < threshold] = 0
img_f[img_f >= threshold] = 255
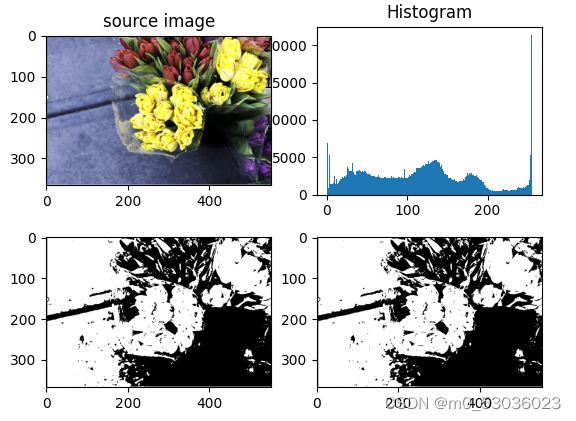
plt.subplot(221), plt.imshow(image_RGB)
plt.title("source image")
plt.subplot(222), plt.hist(image.ravel(), 256)
plt.title("Histogram")
plt.subplot(223), plt.imshow(img_f, "gray")
image_gray = cv.cvtColor(image, cv.COLOR_BGR2GRAY) # 以灰度方法读取图像
ret1, th1 = cv.threshold(image_gray, 0, 255, cv.THRESH_OTSU) # 方法选择为THRESH_OTSU
plt.subplot(224), plt.imshow(th1, "gray")
plt.show()
print("我的方法 threshold is:" + str(threshold))
print("调用cv库 threshold is:" + str(ret1))
toc = timer()
print("运行耗时:", toc - tic) # 输出的时间,秒为单位
GA.py
import random
import numpy as np
class GA:
def __init__(self, img, N):
# 传入参数img为灰度图像直方图 (0-255灰度值出现的频数),初始种群个体数N
self.img = img
self.N = N
self.length = 8 # 阈值在0-255的灰度值之间 需要8bit
self.species = random.sample(range(256), self.N) # 初始化种群数N的种群 随机生成
self.variation_rate = 0.1 # 变异率
self.strong_rate = 0.3 # 选择时直接留下前strong_rate的个体
self.select_rate = 0.5 # 选择时1-strong_rate随机保存0.3的个体
def fitDegreeEstimation(self, individual): # 计算适应度
if individual == 0:
return 0.0
sum_background = 0
sum_target = 0
sum1 = 1
sum2 = 1
for i in range(256):
if i < individual:
sum_background += i * self.img[i]
sum1 += self.img[i]
else:
sum_target += i * self.img[i]
sum2 += self.img[i]
u_background = sum_background / sum1
u_target = sum_target / sum2
w_background = np.sum(self.img[0:individual - 1]) / np.sum(self.img)
w_target = 1 - w_background
g = w_target * w_background * (u_target - u_background) * (u_target - u_background)
return g
def selectIndividual(self):
fitness = []
for i in self.species:
fitness.append([self.fitDegreeEstimation(i), i])
fitness.sort(reverse=True) # 对种群中所有个体按照适应度快速排序,适应度高的在前面
f = [i[1] for i in fitness] # 取fitness的第二列
parents = list(f[0:int(self.N * self.strong_rate)]) # 适应度强的直接保存
for i in f[int(self.N * self.strong_rate) + 1:self.N]:
if np.random.random() < self.select_rate:
parents.append(i) # 从剩下的个体中按select_rate随机选择
return parents
def cross(self, parents):
children = []
children_count = self.N - len(parents)
while children_count > len(children):
dad_idx = np.random.randint(0, len(parents)) # 选择父集下标
mom_idx = np.random.randint(0, len(parents))
if dad_idx != mom_idx:
# 随机选择交叉点 一共8bit
position = np.random.randint(0, self.length)
move = 1 # move应该从1开始 如果从0开始则概率不同
for i in range(position):
move = move | (i << 1) # i向左移一位
# 前position-1位用父亲基因位 其他位用母亲基因位
child = ((parents[dad_idx] & move) | (parents[mom_idx] & (~move)))
children.append(child)
self.species = parents + children
def variation(self):
# 将交叉操作产生的种群中的个体按照变异率进行改变
for i in self.species:
if np.random.random() < self.variation_rate:
# 如果随机数小于变异率
pos = np.random.randint(0, self.length) # 随机选择变异点
i = i ^ (1 << pos) # 1向左移pos位 高位丢弃 低位补零 #在 pos+1 位处取反
def evolution(self):
# 完成选择 交叉 变异的进化过程
parents = self.selectIndividual()
self.cross(parents)
self.variation()
def threshold(self):
# 获取最佳阈值
fitness = []
for i in self.species:
fitness.append([self.fitDegreeEstimation(i), i])
fitness.sort(reverse=True) # 对种群中所有个体按照适应度快速排序,适应度高的在前面
f = [i[1] for i in fitness] # 取fitness的第二列
return f[0]
运行效果
遇到的坑
import cv2下载 cv2 包出错,原因:cv2 的包名是opencv-python
参考资料:
https://blog.csdn.net/qauchangqingwei/article/details/80943076(灰度概念理解)
https://blog.csdn.net/weixin_53056212/article/details/124397351 (参考代码)