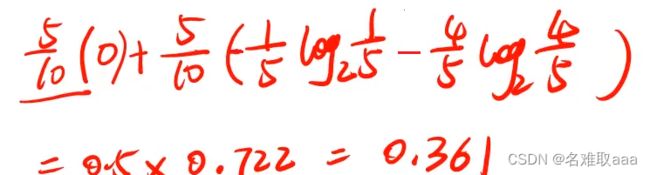机器学习之決策樹

---

前言

随着人工智能的不断发展，机器学习这门技术也越来越重要，很多人都开启了学习机器学习，本文就介绍了机器学习的基础内容之決策樹

---

决策树是什么？

决策树(Decision Tree） 是在已知各种情况发生概率的基础上，通过构成决策树来求取净现值的期望值大于等于零的概率，评价项目风险，判断其可行性的决策分析方法，是直观运用概率分析的一种图解法。由于这种决策分支画成图形很像一棵树的枝干，故称决策树。在机器学习中，决策树是一个预测模型，他代表的是对象属性与对象值之间的一种映射关系。Entropy = 系统的凌乱程度，使用算法ID3, C4.5和C5.0生成树算法使用熵。这一度量是基于信息学理论中熵的概念。
决策树是一种树形结构，其中每个内部节点表示一个属性上的测试，每个分支代表一个测试输出，每个叶节点代表一种类别。
分类树（决策树）是一种十分常用的分类方法。它是一种监督学习，所谓监督学习就是给定一堆样本，每个样本都有一组属性和一个类别，这些类别是事先确定的，那么通过学习得到一个分类器，这个分类器能够对新出现的对象给出正确的分类。这样的机器学习就被称之为监督学习。

決策樹的组成

□——决策点，是对几种可能方案的选择，即最后选择的最佳方案。如果决策属于多级决策，则决策树的中间可以有多个决策点，以决策树根部的决策点为最终决策方案。
○——状态节点，代表备选方案的经济效果（期望值），通过各状态节点的经济效果的对比，按照一定的决策标准就可以选出最佳方案。由状态节点引出的分支称为概率枝，概率枝的数目表示可能出现的自然状态数目每个分枝上要注明该状态出现的概率。
△——结果节点，将每个方案在各种自然状态下取得的损益值标注于结果节点的右端。

決策樹的特點

决策树的众多特性之一就是， 它不需要太多的数据预处理， 尤其是不需要进行特征的缩放或者归一化。

優點

• 计算量小，运算速度快
• 判断步骤清晰，易于理解

缺點

• 对连续性的字段比较难预测。
• 对有时间顺序的数据，需要很多预处理的工作。
• 当类别太多时，错误可能就会增加的比较快。
• 一般的算法分类的时候，只是根据一个字段来分类。

邏輯回歸VS決策樹

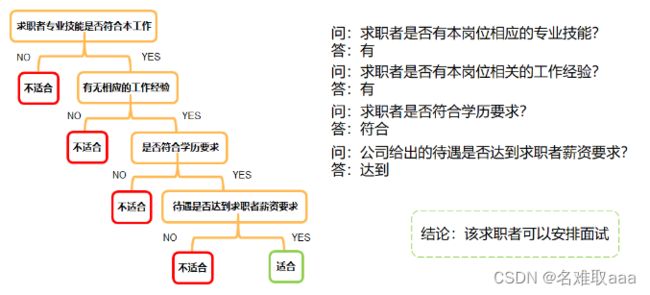
任务：根据求职者的相应技能、工作经验、学历背景和薪资要求判断能否安排该求职者面试。

邏輯回歸模型框架

決策樹模型框架

決策樹求解

決策樹是一种基于样本分布概率，以树形结构的方式，实现多层判断从而确定目标所属类别

根据数据集D的分布，生成树形结构，实现最终类别判断

例子

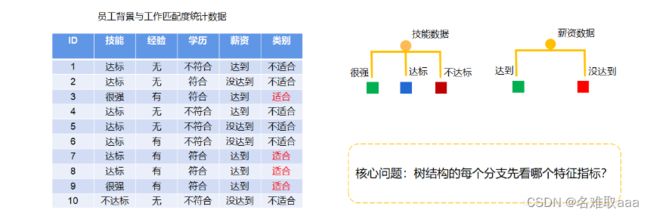
这里有4个判断条件，在我们建立决策树模型框架时，应该将哪一个条件作为第一个判断条件呢？是先根据动力数据，看用户的动力属于很强、一般、很弱哪一类，然后进行下面的判断，还是先根据时间数据，看用户是否有时间，然后再进行下面的判断呢？不同的特征会决定不同的决策树，所以我们在建立决策树模型框架时就应该考虑将每个条件放在适合它的位置上，以此来建立一个最好的决策树模型。

实现该目标常用的有3种求解方法：ID3、C4.5、CART

ID3

利用信息熵原理选择信息增益最大的属性作为分类属性，依次确定决策树的分枝，完成决策树的构造

信息熵（entropy）是度量随机变量不确定性的指标，熵越大，样本的不确定性就越大。假定当前样本集合D中第k类样本所占的比例为pk，则D的信息熵为：

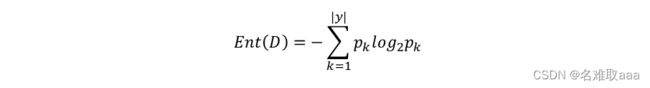
Ent(D)的值越小，样本分布的不确定性越小。

目标：划分后样本分布不确定性尽可能小，即划分后信息熵小，信息增益大

上述例子为例：


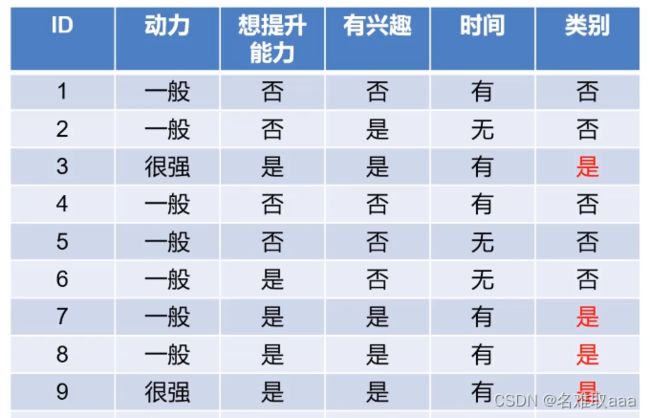
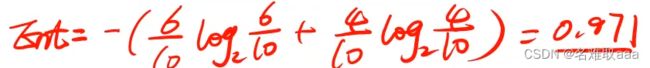
最开始类别那一栏只有是和否，其中"否"占比0.6，"是"占比0.4，可计算出Ent。

这里以兴趣为例：“是”和“否”各占一半，然后“否”对应的类别全为“否”，“是“对应的类别有一个为”否“，其它为”是“。”否“对应的标签为0。”是“对应的标签为1，则有：

以同样的方式去计算其它属性下的信息增益，则有：

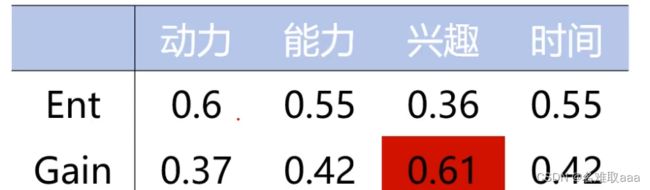
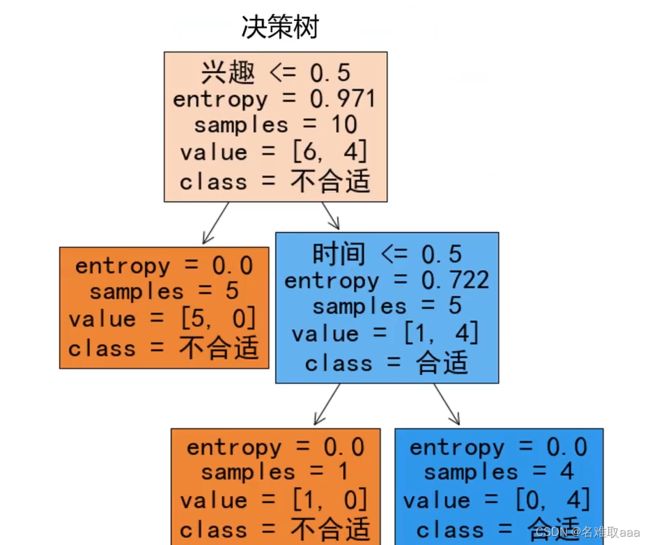
可以发现以兴趣进行划分，信息增益是最大的，此时以兴趣为节点划分好的数据的不确定性是最小的，所以会将兴趣作为决策树的第一个节点。如下圖：

C4.5

C4.5算法继承了ID3算法的优点，并在以下几方面对ID3算法进行了改进：

1. 用信息增益率来选择属性，克服了用信息增益选择属性时偏向选择取值多的属性的不足；
2. 在树构造过程中进行剪枝；
3. 能够完成对连续属性的离散化处理；
4. 能够对不完整数据进行处理。

C4.5算法的优点：产生的分类规则易于理解，准确率较高。其缺点是：在构造树的过程中，需要对数据集进行多次的顺序扫描和排序，因而导致算法的低效。此外，C4.5只适合于能够驻留于内存的数据集，当训练集大得无法在内存容纳时程序无法运行。

具体算法步骤如下：

1. 创建节点N
2. 如果训练集为空，在返回节点N标记为Failure
3. 如果训练集中的所有记录都属于同一个类别，则以该类别标记节点N
4. 如果候选属性为空，则返回N作为叶节点，标记为训练集中最普通的类；
5. for each 候选属性 attribute_list
6. if 候选属性是连续的then
7. 对该属性进行离散化
8. 选择候选属性attribute_list中具有最高信息增益率的属性D
9. 标记节点N为属性D
10. for each 属性D的一致值d
11. 由节点N长出一个条件为D=d的分支
12. 设s是训练集中D=d的训练样本的集合
13. if s为空
14. 加上一个树叶，标记为训练集中最普通的类
15. else加上一个有C4.5（R - {D},C，s）返回的点

CART

背景：
分类与回归树(CART——Classification And Regression Tree)) 是一种非常有趣并且十分有效的非参数分类和回归方法。它通过构建二叉树达到预测目的。
分类与回归树CART 模型最早由Breiman 等人提出，已经在统计领域和数据挖掘技术中普遍使用。它采用与传统统计学完全不同的方式构建预测准则，它是以二叉树的形式给出，易于理解、使用和解释。由CART 模型构建的预测树在很多情况下比常用的统计方法构建的代数学预测准则更加准确，且数据越复杂、变量越多，算法的优越性就越显著。模型的关键是预测准则的构建，准确的。
定义：
分类和回归首先利用已知的多变量数据构建预测准则, 进而根据其它变量值对一个变量进行预测。在分类中, 人们往往先对某一客体进行各种测量, 然后利用一定的分类准则确定该客体归属那一类。例如, 给定某一化石的鉴定特征, 预测该化石属那一科、那一属, 甚至那一种。另外一个例子是, 已知某一地区的地质和物化探信息, 预测该区是否有矿。回归则与分类不同, 它被用来预测客体的某一数值, 而不是客体的归类。例如, 给定某一地区的矿产资源特征, 预测该区的资源量。

實戰

本次是對ID3的實戰，使用最經典的鳶尾花數據集

任務：

1. 基於iris_data.csv數據，建立決策樹模型，評估模型表現
2. 可視化決策樹結構
3. 修改min_samples_leaf參數，對比模型結果

#load the data
import pandas as pd
import numpy as np
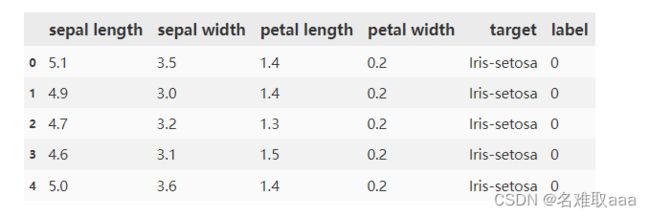
data = pd.read_csv('iris_data.csv')
data.head()

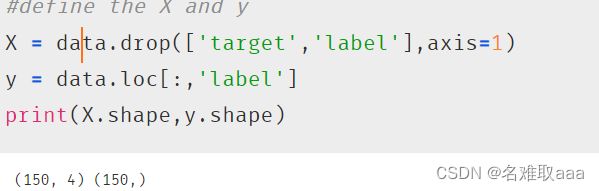
#define the X and y
X = data.drop(['target','label'],axis=1)
y = data.loc[:,'label']
print(X.shape,y.shape)

看一下X和y的數據以及維度確認沒有問題

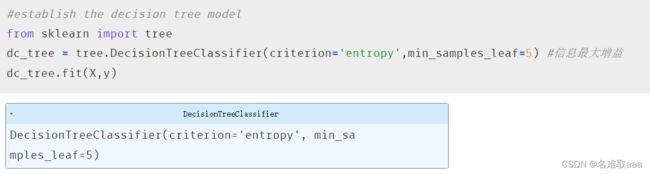
#establish the decision tree model
from sklearn import tree
dc_tree = tree.DecisionTreeClassifier(criterion='entropy',min_samples_leaf=5) #信息最大增益
dc_tree.fit(X,y)

訓練模型，直接導入決策樹的包建立實例就好了，這裏min_samples_leaf會影響最後決策樹的深度

#evaluate the model
y_predict = dc_tree.predict(X)
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y,y_predict)
print(accuracy)

評估模型，看一下accuracy_score分數 百分之九十七也是很不錯的了

#visualize the tree
from matplotlib import pyplot as plt
fig = plt.figure(figsize=(10,10))
tree.plot_tree(dc_tree)

可視化看一下


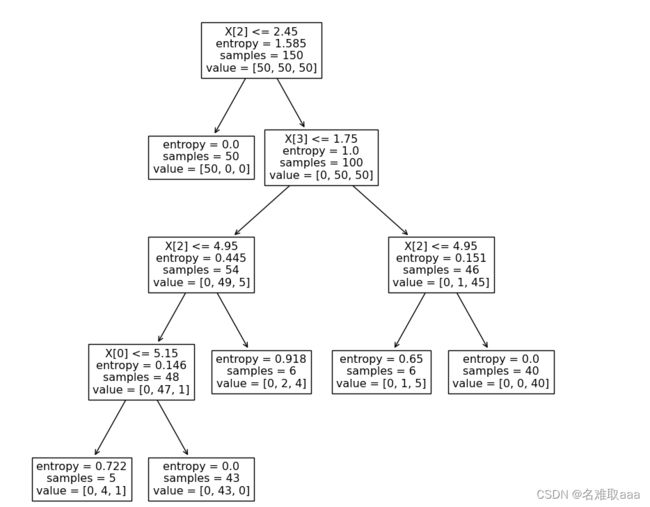
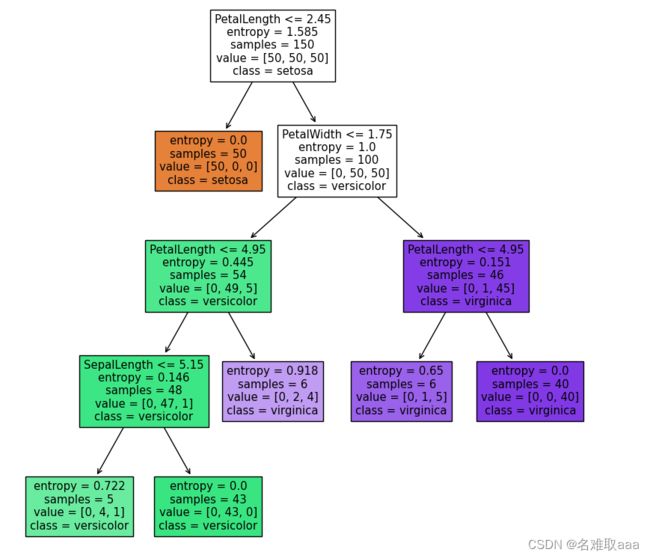
也可以在plot_tree加一些參數將同一類用同一個顔色區別，并且將x[0]x[1]x[2]等等起個名字更方便看

#visualize the tree
from matplotlib import pyplot as plt
fig = plt.figure(figsize=(10,10))
tree.plot_tree(dc_tree,filled='True'
               ,feature_names=['SepalLength', 'SepalWidth', 'PetalLength', 'PetalWidth']
               ,class_names=['setosa','versicolor','virginica'])

這樣就好看也明顯一點了

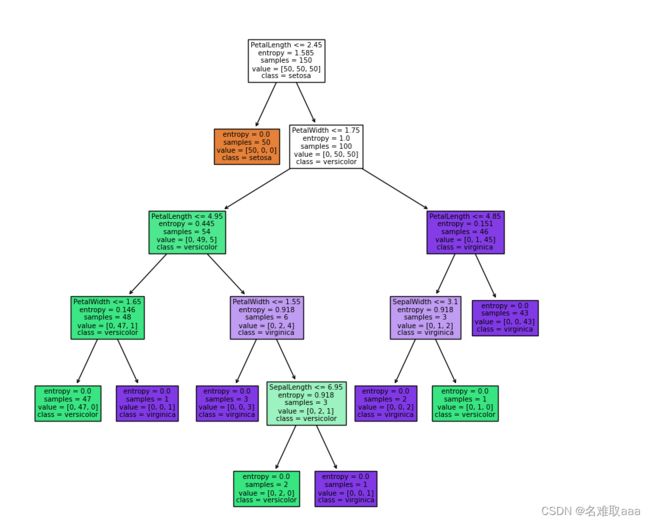
修改min_samples_leaf參數，對比模型結果

dc_tree = tree.DecisionTreeClassifier(criterion='entropy',min_samples_leaf=1) #信息最大增益
dc_tree.fit(X,y)

#visualize the tree
from matplotlib import pyplot as plt
fig = plt.figure(figsize=(10,10))
tree.plot_tree(dc_tree,filled='True'
               ,feature_names=['SepalLength', 'SepalWidth', 'PetalLength', 'PetalWidth']
               ,class_names=['setosa','versicolor','virginica'])

一樣可視化看一下，可以看出分的更細了而且樹的深度更深了

圖中的屬性：

samples属性统计出它应用于多少个训练样本实例。如，开始有150组例子
value属性告诉你这个节点对于每一个类别的样例有多少个。如：右下角的节点中包含 0 个 Iris-Setosa，1 个 Iris-Versicolor 和 45 个 Iris-Virginica。
Gini属性用于测量它的纯度：如果一个节点包含的所有训练样例全都是同一类别的，我们就说这个节点是纯的（Gini=0）。基尼不纯度的公式在下面，具体的用处我们稍后再说。

總結

這就是本次學習決策樹的筆記
附上數據集和源碼
鏈接：https://github.com/fbozhang/python/tree/master/jupyter